基于BIM的三维地形自动修正和拟合方法

2020-01-09周清华张忠良黄新文

铁道勘察 2020年1期

周清华张忠良李纯黄新文

(中铁工程设计咨询集团有限公司，北京 100055)

1 概述

自“铁路BIM联盟”成立以来，已确定了“以铁路标准研究为引导，以BIM试点项目为依托，以协同设计交付和族库管理为抓手”的思想方法与行动指南[1-2]。目前，已制定了《铁路工程实体分解指南》[3]、《铁路工程信息模型分类与编码标准》[4]、《铁路工程信息模型数据存储标准》[5]等11项标准，组织成员单位依托中国铁路总公司设定的BIM试点项目，对铁路线、桥、隧、站、四电等各专业进行系统研究，推动了BIM在铁路场景中落地[6-7]。

随着多个铁路总公司设定的BIM试点项目的完成，铁路BIM规范不断完善，铁路BIM技术应用也逐渐从初期的根据已有二维设计成果翻模创建BIM模型，向利用BIM技术进行三维正向设计发展[8-9]。铁路BIM正向设计中，准确直观的三维地形基准数据是必不可少的。现有BIM设计软件中生成三维地形模型的方法主要为：首先导入数字高程模型或者等高线以及高程点等矢量数据，然后采用三角剖分方法直接模拟生成[10]。该方法生成地形面的速度较快，但是随着项目的进行，如果后期需要修改或提升原有三维地形面精度，则需先返回原始测绘数据进行改正，然后再次生成三角面，或是在BIM设计软件中手动逐点调整，这样的处理方法不仅效率低下，还容易导致地形面精度不足。以下研究一种三维地形的自动拟合和修正方法，将算法直接集成到BIM设计软件，可为铁路BIM设计高效地提供准确的三维地形数据。

2 三维地形自动拟合和修正

2.1 自动拟合原理

在BIM设计软件中，三维地形面的表达多采用不规则三角网模型(TIN)。TIN方法是将区域内离散点以某种相对合理的方法连接起来，如delaunay三角网方法，此方法不会产生交叉的三角面，也能最大限度地避免形成狭长形态的三角形(如图1所示)[11]。

图1 Delaunay三角网

采用delaunay三角网方法表达三维地形面时有个缺点：当特征点、线密度不够时，表达的地形面起伏变化不连续，三角面片之间过渡突兀，显示效果不佳，如图2所示。

图2 地形起伏不连续状态

以下提出的三维地形面自动拟合和修正方法是一种基于稀疏点云的曲面重构方法[12]。利用特征点、线的坐标作为样本构建矩阵，引入回归模型和随机函数，根据预测方差最小原则求取最终地形面参数。为保证拟合面起伏变化的连续性，回归模型采用高斯核函数，此方法不仅可以保持拟合曲面在原有特征点、线处的精度，而且可以拟合出一个连续变化的三维空间曲面[13-15]。同时，当构建矩阵的样本为新增高精度特征点线到既有地形面的差距时，可以拟合出一个顾及原始地形特征的地形面，其起伏变化连续且精度得到提升。

2.2 实现步骤

三维地形自动拟合和修正的总体思路为：根据输入样本数据(高精度特征点、线数据)，采用基于高斯过程的回归模型，通过计算最小协方差得到最优回归参数，根据拟合地形面参数计算修正后的地面坐标值，同时采用双线性内插方法计算标准格网点的坐标值，利用这些格网点生成起伏变化连续的地形面[17]。

根据算法原理，利用少量特征点线直接拟合生成地形面的输入内容为：特征点线坐标集合((xi，yi，zi)，i=1…m)；利用高精度特征点线修正既有三维地形面的输入内容为： (xi，yi，Δzi)，i=1…m。其中，Δz为高精度特征点线到既有面的高差。算法的主要步骤如下。

(1)假设有m个样本，将其分解成平面坐标集合S=[s1…si…sm]T，si∈IRn和高程集合Y=[y1…yi…ym]T，yi∈IR；

(2)对S和Z进行z-score标准化(也叫标注差标准化)处理，经过预处理的数据符合标准正态分布[17]，即

u[S:，j]=0;V[S:，j，S:，j]=1;j=1，…，n

(1)

u[Y:]=0;V[Y:，Y:]=1

(2)

式(1)、式(2)中，u和V分布代表数据的均值和协方差。

(3)引入回归模型F和一个随机函数Z(随机过程)[18-19]

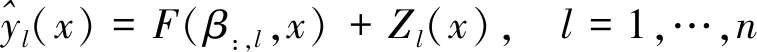
(3)

其中：

F(β:，l，x) =β1f1(x)+…+βnfn(x)=

[f1(x)+…+fn(x)]β:=f(x)Tβ:

(4)

{βk}表示回归参数，假定随机过程Z的均值为0且协方差满足

E[Z(w)Z(x)]=σ2R(θ，w，x)

(5)

其中，Var[z(x)]=σ2，R(θ，w，x)是以初始设定的θ为参数的相关函数。为保证拟合后地形面起伏变化连续，采用高斯核函数，本方案采用的回归模型为线性回归模型。

(f(x)Tβ+z(x))=c(x)TZ-z(x)+

(FTc(x)-f(x))Tβ

(6)

其中，F=[f(s1)…f(sm)]T，Z=[z1…zm]T，为保证无偏要求，FTc(x)-f(x)=0，即

f(x)=FTc(x)

(7)

因此，式(6)的方差为

E[(c(x)TZ-z(x))2]=

E[z2+c(x)TZZTc(x)-2c(x)TZz]=

σ2(1+c(x)TRc(x)-2c(x)Tr(x)]

(8)

其中Rij=R(θ，si，sj)，i，j=1…mr(x)=[R(θ，s1，x)…R(θ，sm，x)]T

(5)根据预测方差最小原则，将c(x)的求解问题化为式(7)约束条件下求解式(8)的极值，采用拉格朗日算法求解，最终得

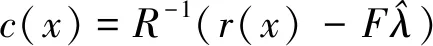
(9)

得到预测的期望方差为

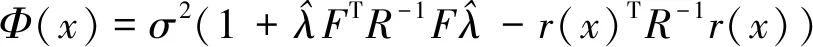
(10)

(6)根据步骤(5)解算的c(x)以及原始地面点平面坐标(x，y)，计算得到拟合或者修正后的z坐标值；如果想内插出标准格网三维地形面数据，可以根据步骤(5)解算的c(x)，内插出标准网格点上的坐标值。

(7)将步骤(6)得出的新三维坐标集导入BIM设计软件中，重新构建三维地形面模型，提供给其他设计专业使用。

3 铁路BIM工程中的应用

以上提出的方法不仅可以利用少量特征点、线拟合出地形曲面，也可以修正得到顾及原始三维地形面地形特征，起伏变化连续、可视化效果较好的三维地形面。该方法已在京张高铁BIM设计中得到广泛应用：图3是利用特征线，采用传统delaunay三角剖分生成的地形面，图4是拟合得到的地形曲面。可以看出，采用拟合方法得到的地形面变化连续，可视化效果更好。