行星悬浮轨道保持控制研究*

李政广， 袁长清，于海莉，左晨熠

0 引 言

太阳帆是一种新型的航天器推进方式，其推进力来源于太阳的辐射光压力.和电推进、离子推进等推进方式一样，太阳帆推进同属于连续小推力的推进方式[1].相比传统推进方式，太阳帆推进所需的能量从太阳光的辐射压力中获得，不需要消耗任何的燃料，航天器既不会产生羽流污染、同时也具有更长的使用寿命.目前为止，如日本宇宙航空研究开发机构(JAXA)研制的IKAROS[2]、美国国家航空航天局(NASA)研制的NanoSail-D2[3]等太阳帆推进航天器，均已成功发射并在轨展开，完成预定的科研任务，证明了太阳帆推进的可行性.

太阳光辐射压力产生的加速度远小于传统的化学推进器，但由于太阳光压力可持续作用在太阳帆帆面上，在连续推力的作用下，航天器可以实现非开普勒轨道等特殊的轨道[4].行星悬浮轨道就是其中一类特殊的非开普勒轨道，它由航天器的推进力与太阳、行星等天体的引力相互平衡，形成的垂直于太阳与行星连线方向的一种周期轨道，其轨道的独特性可为深空探测、中继通讯等航天任务提供理想的轨道平台，在高分辨率深空探测、深空中继通信等领域显示出巨大的应用前景.

在太阳帆航天器悬浮轨道的研究中，BOOKLESS等[5]研究总结了多种形式的行星悬浮轨道的动力学特性，并归纳出悬浮轨道的稳定区域.GONG等[6]针对地球及火星，推导出悬浮轨道附近编队的线性化相对运动方程，并对轨道稳定区域进行了分析.OZIMEK[7]基于地-月三体系统研究了悬浮于月球极地上空的悬浮轨道问题，并用数值方法对该问题进行了求解.陈翠红等[8]在Bookless等研究的基础上，基于Hamilton方程及Hamilton-Jacobi理论，对行星悬浮轨道稳定性进行了进一步的分析.覃曌华等[9]将太阳能电推进与太阳帆推进相结合，设计了地球同步悬浮轨道的控制率.钱航等[10]基于极坐标系，对日心悬浮轨道的保持问题进行了研究，根据推导出的动力学方程提出了一种主动控制律.张楷田等[11]基于圆形限制性三体问题(CRTBP)，对太阳帆推进与电推进组成的推力混合航天器在日心悬浮轨道处的动力学进行了探究，并设计了相应的轨道保持方法对悬浮轨道进行保持控制.其后，两位学者又建立了悬浮轨道处的太阳帆编队动力学方程，并对编队系统进行了相应的控制研究[12].

本文以地球为例，在现有基于二体动力学模型研究的基础上[4,5,6,10]，建立太阳帆在太阳-行星连线方向的悬浮轨道动力学方程.针对模型的动力学特性并考虑轨道出现初始小扰动的情况，设计LQR控制器与基于遗传算法改进的LQR控制器，通过数值仿真对设计的控制器进行分析对比，各状态变量通过控制器快速收敛至期望值，验证了设计方法的有效性.

1 太阳帆轨道动力学

1.1 建立坐标系

由于地球周围太阳光的压力场变化范围仅有4×10-3，因此可以将地球周围的光压力场看作均匀分布的[4,6].因为地球公转角速度相比其周围卫星的角速度可忽略不计，故本文研究的问题中，地球绕太阳的旋转可忽略.如图1所示，以地球质心为原点，建立惯性坐标系O-XYZ：X轴指向地球公转角速度方向，Z轴指向为日-地连线方向，面YOZ在黄道面内，且O-XYZ构成右手坐标系.

定义太阳帆运行在与日-地连线(即Z轴)垂直的平面上，轨道高度矢量为z，轨道半径矢量为r，假设太阳帆运行角速度ω为定值，且方向同Z轴相同.

1.2 太阳帆动力学建模

假设太阳光沿Z轴平行射向航天器，只考虑地球引力及太阳光压力作用，地球与太阳帆构成的二体系统中，太阳帆的动力学方程可写为

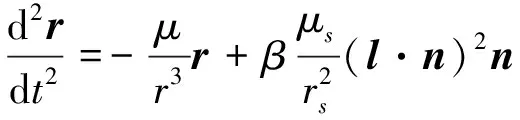
(1)

式中，地心指向航天器的位置矢量由r表示；μ为地心引力常数；β为太阳帆的光压因子；μs为日心引力常数；rs表示日心到太阳帆的距离.

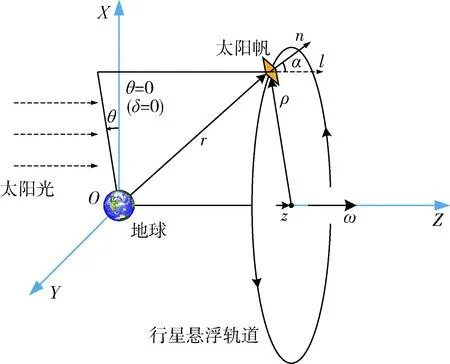
图1 行星悬浮轨道坐标系Fig.1 Planet-centred non-Keplerian orbit frame of reference

在描述太阳帆姿态时，通常使用锥角α和转角δ来表述[13].锥角α为太阳帆面法向矢量n与太阳光线矢量l之间的夹角，转角δ表示从某一参考位置出发太阳帆法线绕太阳光线转过的角度.本文取X轴为转角δ的参考方向，由于太阳帆轨道角速度为定值，因此本文中转角δ可由太阳帆在XOY平面上投影角度θ来表示.由于假设地球周围太阳光压场均匀，太阳光线矢量可表示为l=[0 0 1]T.根据定义，在惯性系O-XYZ中，太阳帆面法向量n可表示为

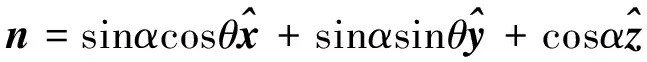
(2)

转化为柱坐标形式，n可表示为

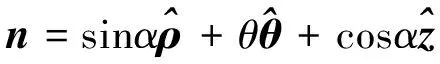
(3)

根据导数定义，将ρ和z分别对时间t求二阶导数，得

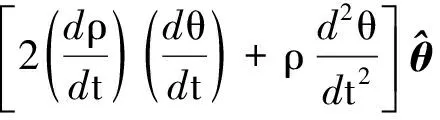
(4)

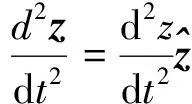
(5)

由图1中的几何关系可以得到

r=ρ+z

(6)

将式(5)带入式(6)，得到太阳帆悬浮轨道动力学方程

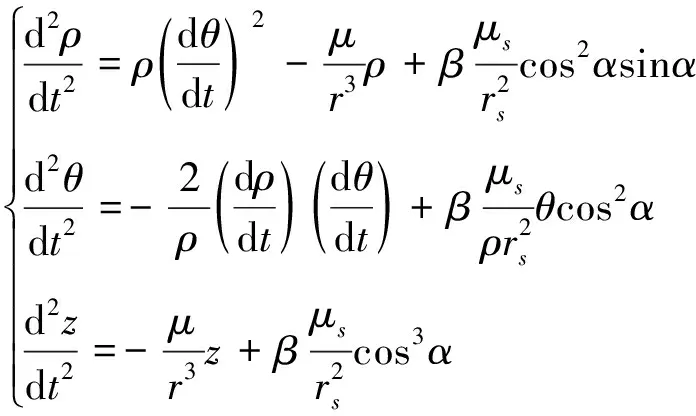
(7)

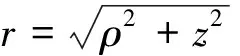
设ρ0和ω0分别为初始的悬浮半径和角速度大小，对式(7)中的辐角公式运用常数变易法进行积分可得

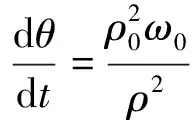
(8)

由结果易得，太阳帆所在轨道平面运动的角动量是守恒的，记太阳帆角动量为

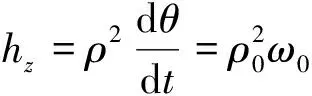
(9)

为保证太阳帆运行在特定轨道上，所需的太阳帆姿态角α可由式(10)求出，即[4]

(10)

1.3 系统线性化

将单位进行归一化处理，取地球半径为单位长度L，地心引力常数μ=1，用无量纲化的太阳光压加速度κ表示以1个地球半径的重力加速度为单位的太阳辐射压力加速度.

由于假定太阳帆沿轨道平面运行的角速度是恒定的，轨道的幅角θ不需要控制，因此太阳帆动力学方程(7)中的幅角θ项可忽略不做考虑.将太阳帆角动量方程(9)带入动力学方程(7)，太阳帆动力学方程可由轨道半径ρ和高度z表示为

(11)

将位置摄动ρ、z表示为ρ=ρ0+δp和z=z0+δz；将姿态角摄动α表示为α=α0+δα，作为系统内控制输入.对式(11)使用泰勒展开并忽略高阶项，可得线性动力学方程为

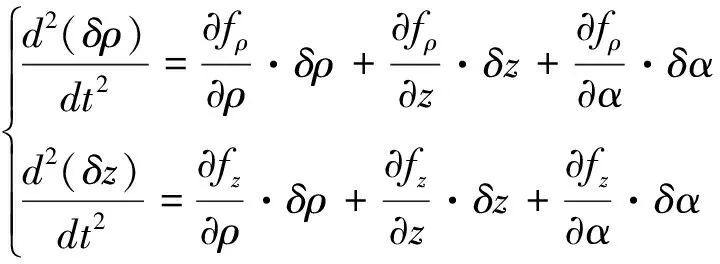
(12)

2 控制器设计

2.1 LQR控制器

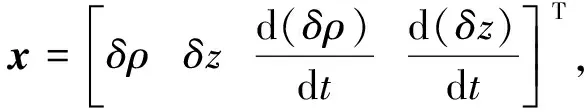
动力学方程(12)可写成状态方程的形式

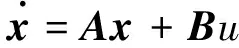
(13)

状态误差方程如式(13)～(15)所示，x0为初始误差.取如下二次型性能指标函数

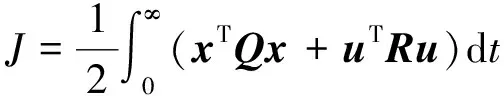
(16)

式中,分别用矩阵Q和R来描述状态变量和控制变量的加权矩阵.其中，Q为半正定矩阵、R为正定矩阵.此LQR问题相应的代数Riccati方程为

PA+ATP-PBR-1BTP+Q=0

(17)

通过求该代数方程，可以得到P矩阵，从而得到最优控制

u=-R-1BTPx

(18)

2.2 遗传算法改进的LQR控制器

传统LQR控制器中，其最优性完全取决于加权矩阵Q、R的选择.而Q、R的确定并没有具体的解析方法，只能通过“人为的”经验来选择，根据系统的输出结果，不断调整加权矩阵，得到满意的输出响应.这种方法既费时又无法获得最优的加权矩阵.

遗传算法是一种通过模拟生物进化理论发展而来的全局搜索的寻优算法.采用适者生存的原则，在迭代的过程中通过变异、交叉等手段，使种群向最优发展，以此获得最优解.本节利用遗传算法对LQR控制器中的加权矩阵进行寻优搜索，提高LQR的控制效率[16].

为使航天器轨道的位置扰动δρ和δz快速趋于0，并使整个控制过程中所消耗控制能量降到最低，由此，设计LQR控制器的性能指标为

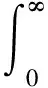
(19)

将式(13)带入式(19)，有

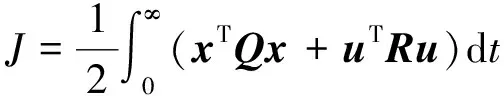
(20)

其中，

最优控制反馈增益矩阵K可调用MATLAB的线性二次最优控制器设计函数获得：

K=LQR(A,B,Q,R)

(21)

由此，所设计的最优控制器控制效果完全取决于加权系数q1、q2、q3的选择，基于遗传算法的LQR控制器加权系数优化过程示意图如图2所示[16].

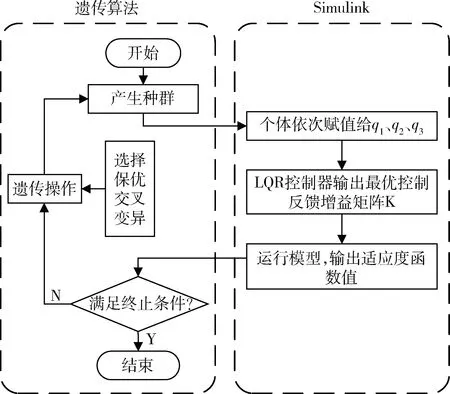
图2 遗传算法优化设计LQR控制器示意图Fig.2 Procedure of genetic algorithm

3 仿真分析

考虑悬浮轨道位置保持问题，选取数值仿真条件如下：标称悬浮轨道半径ρ0=60L(1L=6.371 393×106m)，标称悬浮轨道高度z0=20L；通过公式(10)计算得到维持该轨道稳定时所需的姿态角α=38.214 3°；太阳帆轨道周期与半径为70L的开普勒轨道同步；选取无量纲化的太阳光压加速度κ=2.348×10-4[5].

为验证上述设计的控制器的有效性，对其进行数值仿真分析.设定悬浮轨道半径及高度的初始扰动为δρ=0.001L、δz=0.001L.仿真过程中，将本文设计的遗传算法改进的LQR控制器同传统LQR控制器进行了比较.仿真结果如图3～8所示.

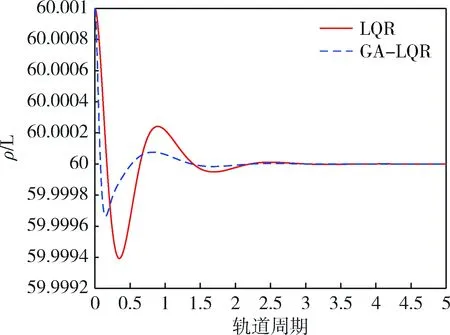
图3 轨道半径变化曲线Fig.3 Track radius graph

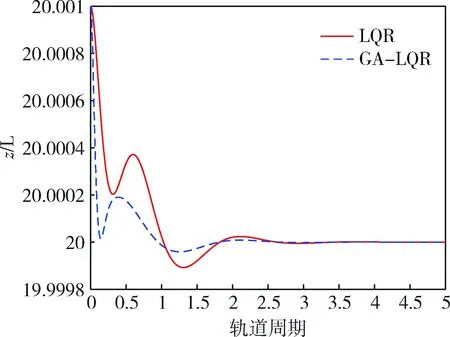
图4 轨道高度变化曲线Fig.4 Track altitude graph

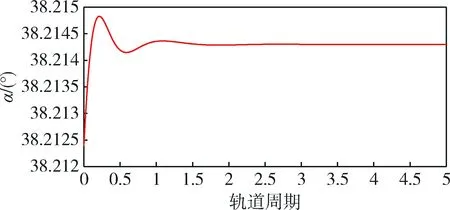
图5 传统LQR控制器下姿态角变化曲线Fig.5 Attitude angle curve by LQR

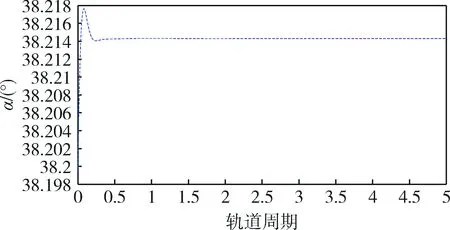
图6 改进的LQR控制器下姿态角变化曲线Fig.6 Attitude angle curve by GA-LQR

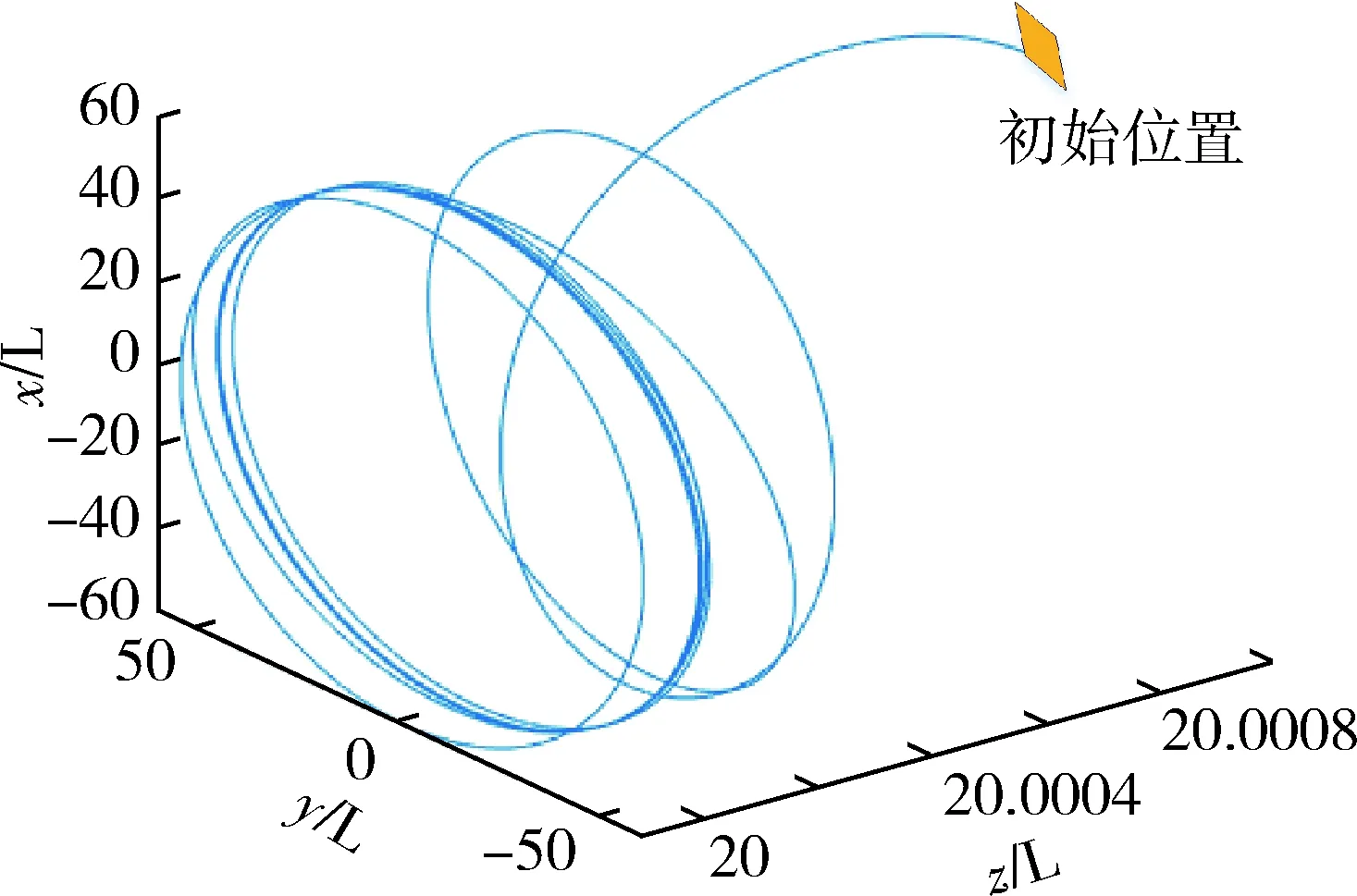
图7 LQR控制器下的轨道变化曲线Fig.7 Track graph by LQR

图8 遗传算法改进控制器下的轨道变化曲线Fig.8 Track graph by GA-LQR

图3、图4为传统LQR控制和遗传算法改进的LQR控制下的航天器轨道位置ρ、z随轨道周期的变化曲线图，由图可以看出采用两种控制器均能够使航天器按照预期要求达到期望状态，在0～5个周期内，位置距离逐渐由初始误差趋近于稳定的理想位置，并保持平衡稳定.同时，比较图5、图6可以发现，改进的LQR控制器下，姿态角能够在较短的轨道周期内快速响应，加快轨道保持稳定.综合对比，在两种控制策略下，遗传算法改进的LQR控制器在控制稳定性和调节时间方面都优于传统LQR控制器.可以看出，遗传算法改进的LQR控制器超调量小，调节时间较短.

图7、图8分别为传统LQR控制器及遗传算法改进的LQR控制器控制后的轨道仿真图，由该图更能直观的看出遗传算法改进的LQR控制器调节时间较短，能够在2.5个轨道周期恢复稳定(传统LQR需4个周期)，控制性能优于传统LQR控制器.

4 结 论

本文主要研究了太阳帆航天器在行星悬浮轨道上的动力学与控制问题.首先推导出行星悬浮轨道处太阳帆动力学方程，考虑该动力学系统的非线性，对动力学方程进行了线性化处理，并设计了遗传算法改进的LQR控制器.为验证该控制器的有效性与控制性能，基于MATLAB/Simulink平台进行数值仿真，与传统LQR控制器进行对比，改进的LQR控制器调解时间短、恢复稳定速度快，性能优于传统LQR控制器.