基于遗传禁忌混合算法的敏捷卫星任务规划
2020-01-09丁祎男田科丰王淑一
丁祎男,田科丰,王淑一
0 引 言
对地观测成像卫星是一类利用卫星遥感器对地球表面、地形地貌、能源矿藏,以及低层大气进行探测从而获取有用信息的一类卫星[1].随着敏捷机动技术的发展,敏捷技术在成像卫星中广泛应用,如美国的WorldView系列卫星,法国的Pleiades星座等.
敏捷成像卫星是断续工作方式,因此需要根据用户需求进行任务规划.卫星任务规划在整个对地观测过程中起着关键作用,其结果直接影响到对地观测卫星系统的观测效率.
目前,国外在卫星任务规划领域的研究持续时间长,技术比较成熟,且相关技术已应用到一些实际的航天任务中,其中,由NASA研制的ASPEN(Automated scheduling and planning environment)是一种地面任务规划系统,使用局部搜索算法,应用范围广、扩展性良好[2].法国LEMAITRE等[3]针对敏捷卫星Pleiades星座的任务规划,提出了约束规划模型,并分析比较了约束规划、贪婪、动态规划以及局部搜索等四种算法.TANGPATTANAKUL等[4]提出了一种基于指标的多目标局部搜索算法,解决多目标观测任务规划问题.国内研究中,黄生俊等[5]针对多星任务规划,综合蚁群算法的反馈特性和模拟退火算法的局部搜索特性,设计了一种基于知识的改进模拟退火算法.郝会成等人针对新一代对地观测敏捷卫星任务规划问题,提出了一种免疫遗传-蚁群混合算法[6].李菊芳等[7]探讨了一类涉及多星、多地面站的成像卫星系统集成调度问题,并提出了一种变邻域禁忌搜索算法.赵萍等[8]对卫星自主任务调度问题构建了基于目标收益及多约束的任务调度模型,并设计了一种改进的自适应遗传算法进行求解.韩传奇等[9]提出了基于成像任务时间及任务均衡度的多指标优化函数,针对所建模型,采用改进的遗传算法,引入资源随机分配的解码策略及精英保留策略,保证了算法的全局收敛性,提高了算法的性能.
以上研究都针对敏捷成像卫星任务规划问题的特点设计了智能优化算法进行求解,得到了较好的优化结果,可以看出智能优化算法在求解卫星任务规划问题上有很大优势.但现有的研究中任务规划模型都较为简单,存在一定的局限性.其中ASPEN系统是面向单颗卫星的任务规划,没有涉及多星的协同调度; LEMAITRE等人的研究中应用的智能优化算法都有各自的缺点,没有使用混合算法来互补;黄生俊等和李菊芳等的研究面向的是非敏捷卫星,没有考虑任务间卫星的姿态转换约束;韩传奇等的研究没有考虑卫星机动能力和能量约束;并且在卫星成像系统多样化的如今,上述提到的研究都没有考虑到多载荷的任务协同调度.
针对这些问题,本文对多星自主任务协同中涉及的任务建模及优化算法进行研究,采用了一种遗传禁忌混合算法,解决多载荷敏捷卫星在星上资源约束条件下的任务优化问题,解决多星多载荷的任务协同分配问题.
1 问题描述
敏捷卫星任务规划可以被描述为约束优化问题.卫星进行成像时必须满足一定的约束条件,以保证成像卫星安全、准确地执行任务.记卫星数量为S,目标点数量为P.
1.1 约束条件
本文考虑的约束包括:
(1) 卫星对目标点的可见性约束
若第p个目标点对第s颗卫星可见,卫星质心指向该目标点的矢量和卫星与地心连线矢量的夹角αsp不能超过卫星的最大偏置能力αsmax.可以表示为:
αsp≤αsmax
(1)
(2) 卫星对目标点的观测时长约束
若第i个可见时间窗口包含第p个目标点,则时间窗口的长度不能小于此目标点需要被观测的时长dp,可以表示为:
Tei-Tsi≥dp
(2)
其中Tsi表示第i个可见时间窗口开始时刻,Tei表示第i个可见时间窗口结束时刻.
(3) 星载传感器类型的约束
本文主要考虑可见光相机和红外相机两种对地观测载荷.其中,配置可见光相机的卫星只能在阳照区观测,配置红外传感器的卫星可以在全轨道周期观测,阳照区优先采用可见光相机观测.
在满足(1)~(3)三个约束的前提下,可以计算出所有卫星对所有目标点的时间窗口.每一个时间窗口可以作为一个元任务,是任务规划模型的基本单位,记元任务数量为N.
(4) 卫星姿态机动能力约束
卫星进行姿态转移的时间受机动能力的约束:
Toei-Tos(i+1)≥Tdimin
(3)
其中Toei表示前一次任务观测结束时间,Tos(i+1)表示此次任务最晚开始观测时间,Tdimin为两次观测姿态转移所需最短时间.
(5) 卫星的星上能源约束
将星上能源简化为观测能量,假设在一个观测周期内第s颗卫星的总观测能量maxEs是有限的.若要执行元任务mi,需要有足够的能量去执行此任务,可以表示为:
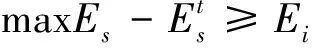
(4)
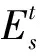
Ei=k1φi+k2dpi
(5)
其中φi、dpi分别为卫星观测元任务mi需要的机动角度、成像时长,k1为机动角度到观测能量的转换系数,k2为观测时长到观测能量的转换系数.
(6) 卫星存储器容量约束
卫星对目标成像时生成成像数据,储存在星载存储器中,经过地面站会向地面站传输之前储存的观测数据,释放存储器空间.假设第s颗卫星存储器容量为maxCs,若要执行元任务mi,需要有足够的存储器可用容量去储存此任务产生的数据,表示为:
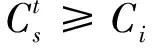
(6)
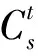
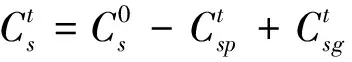
(7)
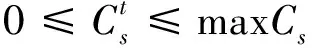
(8)
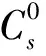
每次成像生成的数据大小和成像时长成正比,每次释放的数据大小和数传时间成正比,可以表示为:
Ci=k3dpi
(9)
Csg=k4dsg
(10)
其中dpi为卫星观测元任务mi的成像时长,dsg为第s颗卫星与第g个地面站的数传时长,k3为成像时长到成像数据的转换系数,k4为数传时长与释放空间大小的转换系数.
(7) 卫星数传约束
若第s颗卫星要向第g个地面站传输数据,则地面站与卫星之间的视线方向在当地的仰角βsg不能小于卫星对地面站可见的最小仰角βmin,可以表示为:
βsg≥βmin
(11)
根据卫星数传约束可以计算出卫星经过地面站的数传时长.
(8) 目标点任务约束
每个目标点都需要被观测一次,且只被一颗卫星观测,对于第p个目标点有:
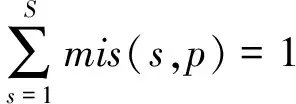
(12)
其中mis(s,p)为第s颗卫星对第p个目标点的执行情况,1表示执行,0表示不执行.此约束条件是为防止在一个观测周期中某一个目标点被多次观测,浪费卫星资源.
由于一个目标点对应多个元任务,且元任务间不可避免的存在时间窗口冲突,再考虑到(4)~(8)约束条件的限制,需要任务分配算法来确定最终的任务序列.
1.2 性能指标
每一个元任务mi包含的目标点pmi都有不同的权重ωi,任务规划的性能指标M为任务序列中所有完成任务对应目标点的权重和.为引导优化算法优先考虑在阳照区采用可见光成像,设定若完成的任务为红外相机在阳照区成像(下文称为载荷不匹配),此任务对应的权重将乘以惩罚系数μ(0<μ<1).本课题选取μ=0.5.性能指标可以表示为:
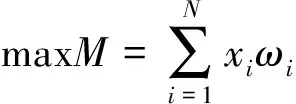
(13)
其中
2 求解算法
多星多载荷任务规划问题是典型的NP困难问题,没有有效的确定性求解算法,传统解决此类问题的主要方法包括遗传算法、禁忌算法等智能优化方法.
遗传算法是基于自然选择和基因遗传学原理的搜索算法,其适用范围广、广域搜索能力强,但也因种群间有很高的局部相似性,存在收敛速度慢,求解时间长的缺点.
禁忌算法模仿人类的记忆功能,使用禁忌表来避免重复搜索,并通过藐视原则来留下优良解,从而保证搜索的多样性,达到全局优化的目的.禁忌算法收敛速度快,求解时间短,但其搜索性能对初始解依赖较大且广域搜索能力不足.
由上可知,遗传算法和禁忌算法有较强的互补性,本文结合两者的优点,使用遗传禁忌混合算法进行求解.求解步骤如下:
1) 对于多星对多目标的观测任务,元任务数量巨大,需要先对元任务进行聚类处理.
2)按照一定的顺序对所有聚类依次应用混合算法进行优化运算,得到每个聚类的最优任务序列.
3) 将所有聚类的最优任务序列合并可以得到整个任务规划问题的最优任务序列.
2.1 元任务聚类方法
本文根据元任务的时间窗口进行聚类,具体步骤为:
1) 设定最小聚类间隔mindt.将元任务序列按照时间窗口开始时刻从前到后排列,遍历所有元任务,如果元任务mi和元任务mi-1的开始时间tsi和结束时间tei-1满足tsi-tei-1>mindt,并且对任意j
2) 得到分割点集合[b1,b2,…bn-1,bn],根据分割点集合可以将元任务序列分割成n+1个聚类.分割成的聚类包含元任务序号分别为为1~b1,b1+1~b2,…,bn+1~N.(N为元任务的总数).
3) 按照所处时间区间的先后顺序处理第l个聚类:
①若l>1,类的种群初始化都是在完成上一个聚类的任务规划后进行的.首先将包含之前类中已经观测过的目标点的元任务去除.
②然后对剩余的元任务进行0-1编码,生成的染色体对应一个任务序列,每一个编码对应一个元任务,0代表该元任务不执行,1代表执行.随机产生多条染色体,构成初始种群,
③进行任务规划运算,生成并存储优化后的任务序列,继续处理下一个聚类.
4) 完成所有聚类的任务规划后,将每个聚类的最优任务序列按处理顺序首尾相连,可以得到整个任务规划的最优序列.
2.2 遗传禁忌混合算法
本文采用嵌入禁忌搜索的混合遗传算法,核心思想是针对遗传算法变异的无序性,使用禁忌搜索代替遗传运算中的变异算子,一般称为禁忌搜索变异算子,记为TSM(tabu search mutation)算子.
基本流程如图1所示,具体如下:
(1) 对染色体对应的任务序列进行冲突处理,根据1.2节计算其性能指标(在优化算法中称为适配值).进而计算种群中每一条染色体的适配值.
(2) 基于轮盘赌的选择运算
设种群大小为n,计算出个体i的适配值为Fi,轮盘赌具体过程如下:
1) 计算个体i被选中遗传到下一代群体的概率为:
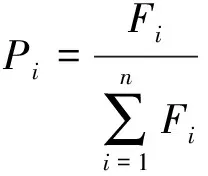
(14)
2) 计算个体i的累计概率:
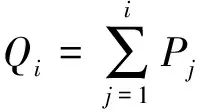
(15)
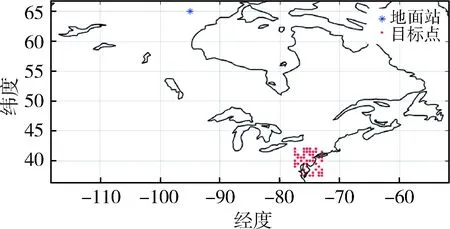
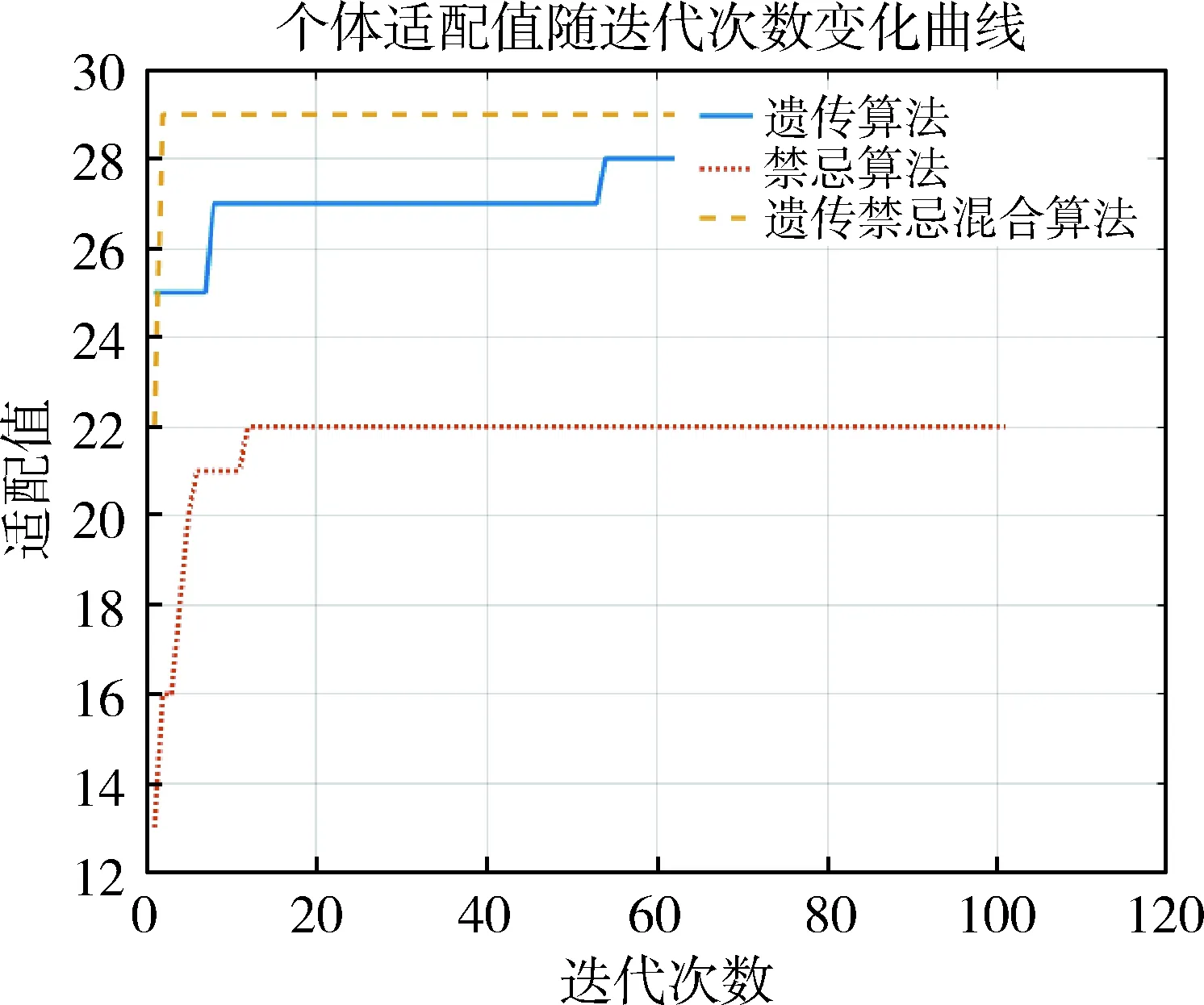
3) 在[0,1]区间内产生一个随机数r,若r (3) 交叉运算 采用多点交叉的方式来跳出局部解. 1) 根据选择出来的父代群体,按顺序取出两个父代进行交叉. 2) 在[0,1]区间内产生一个随机数r,若r (4) 使用TSM算子变异 1) 对于子代种群中的每一个染色体,在[0,1]区间内产生一个随机数r,若r 2) 将当前染色体作为禁忌搜索算法的初始解. 3) 由该初始解产生候选解集,根据解的适配值和禁忌表情况选择最优解,并更新禁忌表. 4) 将最优解作为初始解重复步骤(3),直至完成迭代要求.依次产生新的种群. (5) 以新的种群返回(1),继续进行遗传优化运算,直至得到该聚类对应的最优任务序列. 图1 遗传禁忌混合算法框图Fig.1 Flow chart of genetic-tabu hybrid algorithm 为验证第2节算法的效果,对优化算法进行仿真.仿真平台为:Windows10操作系统下的Matlab2018b,计算机配置为Intel(R) Corei7-7700HQ@ CPU 2.8GHz处理器,16G内存. 设计星座有两个轨道面,每个轨道面有4颗卫星,采用太阳同步轨道.降交点地方时分别为10:30和13:30,仿真周期为86 400 s即一天. 种子卫星轨道根数: 半长轴a=(6 371+500)km 偏心率e=0 倾角i=97.4° 近地点幅角ω=0° 升交点赤经Ω=160° 为充分利用星座的覆盖能力,每个轨道内相邻的两颗卫星相位差为90°,相邻轨道第一颗卫星相位差为45°.每个轨道面内有一颗卫星为红外相机.星座对于赤道上的点的最大重访周期约为2.95 h. 共选取目标点50个,随机分布在78°W~73°W、37°N~42°N之间,设置一个地面站,坐标为95°W,65°N,目标点和地面站分布如图2所示. 图2 目标点和地面站分布示意图Fig.2 Diagram of target points and groundstations distribution 对于遗传算法,理论上种群规模越大、进化代数越多,得到的优化结果越接近最优解,但是随之带来的运算复杂度也会大大增加,根据经验交叉概率应在0.9附近选取,而变异概率不宜大于0.1. 对于禁忌搜索算法,候选集的大小和禁忌长度都会对优化结果产生较大影响,理论上候选集越大,在有限的迭代次数内找到最优解的机会就越大,但会增加运算时间.禁忌长度的选取同实际问题有紧密的联系,同时它决定了计算的复杂性,过短会造成循环的出现,过长又会导致收敛变慢.对于不同问题需要通过仿真验证选取合适的参数. 对于遗传禁忌混合算法,可以充分利用两种优化算法的互补性,在不影响最终优化效果的前提下,调整参数使得运算时间尽可能地减少. 经过多次仿真验证,对于3.1节描述的任务规划模型,采用以下参数可以得到相对满意的结果.令m为聚类中元任务数量. 遗传算法:种群大小为10m,交叉概率为0.9,变异概率为0.09. 为了直观比较分析三种优化算法的优化效果,选取一个聚类的优化过程作具体展示: 此聚类包含40个元任务,40个目标点,总权值为119,优化效果如图3所示. 图3 单聚类优化仿真示意图Fig.3 Optimization result for a single cluster 可以看出,遗传混合算法可以在在很短的代数内达到遗传算法多代迭代的优化结果,禁忌搜索算法虽然收敛迅速,但优化效果不如混合算法. 根据三种算法的具体优化效果,在每个聚类的优化中设置最少迭代次数n,迭代次数大于n后,若连续5代最优解不变,便结束迭代.遗传算法和禁忌算法至少迭代50次,遗传禁忌混合算法至少迭代10次. 对于总体优化任务,共有309个元任务,包含50个目标点,总权重为154.每种优化算法运行30次,仿真结果如表1所示.其中载荷不匹配数量占比为一次任务规划得到的任务序列中,红外相机在阳照区观测次数占观测总次数的比例. 相对于遗传算法,遗传禁忌混合算法适配值标准差减少26.56%,优化耗时减少37.41%,在不影响优化效果的前提下,大大减少了优化时间;相对于禁忌算法,遗传禁忌混合算法适配值平均值提高8.49%,最差适配值提高13.99%,适配值标准差减少51.00%,载荷不匹配占比减少41.14%,混合算法克服了禁忌算法对初值依赖性强,优化效果不稳定的问题. 综上,混合算法继承了遗传算法广域搜索能力强和禁忌算法收敛速度快的特点,优化时间短,优化性能指标高,载荷不匹配数量占比小,有效解决了多星多载荷任务协同分配问题. 表1 任务规划仿真结果Tab.1 Simulation results of mission scheduling 本文采用了一种遗传禁忌混合算法解决多星多载荷任务协同分配问题.针对传统遗传算法求解时间代价大、传统禁忌算法对初始解依赖问题,将禁忌算法嵌入遗传算法作为禁忌算法变异算子,打破种群个体间的局部相似性.仿真结果表明,该算法充分利用了两种算法的互补性,优化效果和收敛速度俱佳.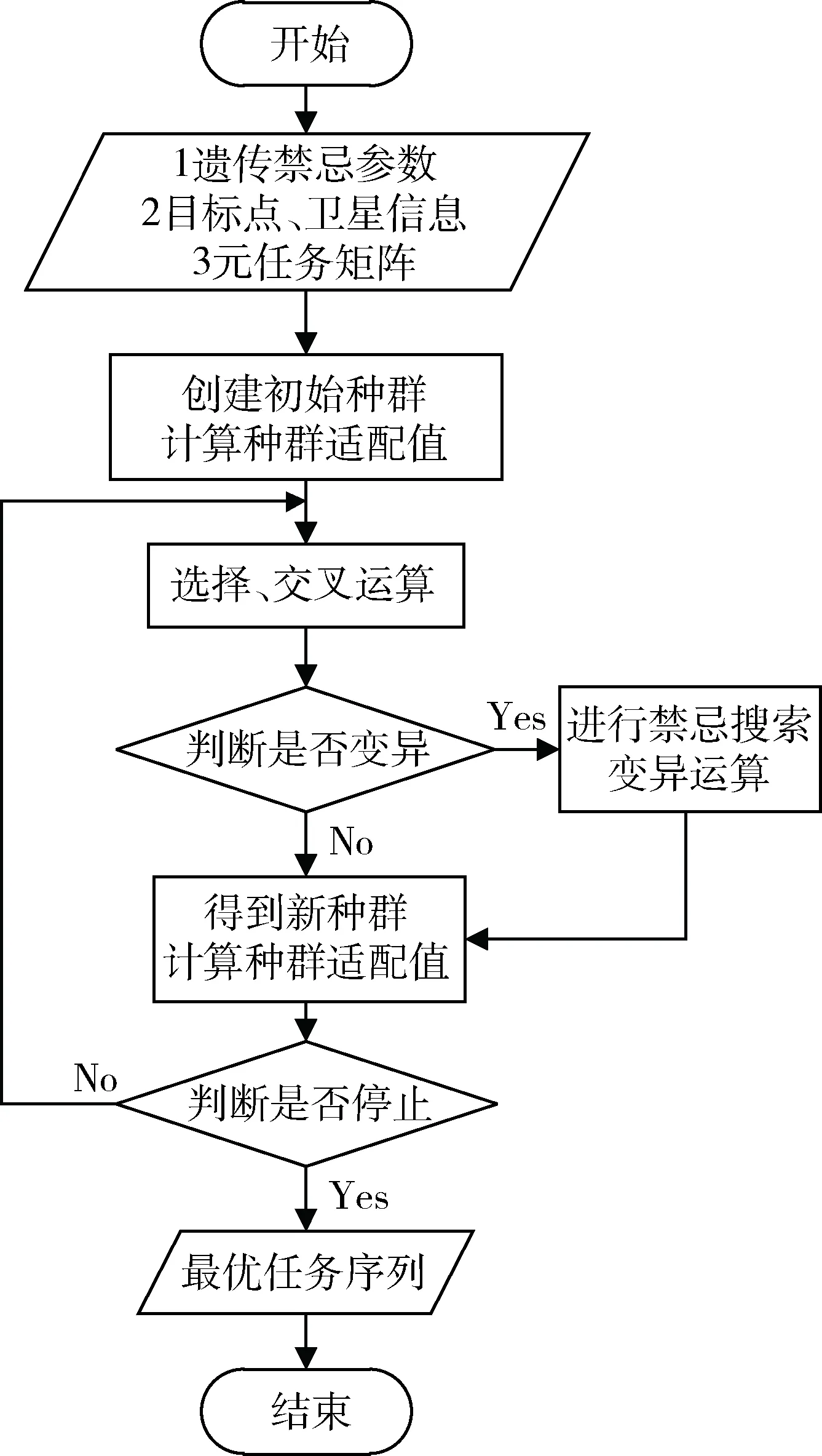
3 仿真与分析
3.1 模型参数
3.2 优化算法参数
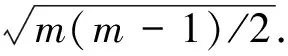
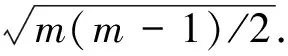
3.3 仿真结果与分析

4 结 论
