煤灰主要成分与流动温度关系预测
2020-01-08刘颖琳王东路
王 超,王 华,刘颖琳,王东路,李 翠
(1.国网山东省电力公司电力科学研究院,山东 济南 250003;2.国家能源集团山东石横热电有限公司,山东 泰安 271621)
0 引言
煤灰熔融性是评价煤炭燃烧和气化的重要指标[1],它直接影响到燃煤电厂锅炉尾部受热面的结渣、堵塞问题[2]。煤灰成分直接影响煤灰熔融特性,复杂而且含量多变导致与煤灰熔融性之间产生一种未知的关系,采取何种措施可以高效准确地找到二者之间的关系是当前研究热点。
对于煤灰熔融特征温度,可以采用角锥法[3]或TMA 定量法[4]直接测定,但这两种方法无法提供某特定温度点下熔渣的性质。基于此,世界各国学者通过创建不同模型的方式预测煤灰熔融特征温度[5-7]。樊泉桂等[8]利用SPSS 软件准确的推导出煤灰熔融特征温度的公式;霍正华[9]运用反向传播(BP)神经网络法来推算煤灰熔融特征温度;王春林[10]认为支持向量机算法能够建立灰熔融性预测模型,并通过遗传算法(GA)优化了该模型的参数。但是这几种模型都有相应的不足[11]:运用SPSS 进行多元回归分析虽然具有很高的相关度,但是适应性很差;BP 神经网络法虽然有很强的适应性,但必须以大量数据为前提;支持向量机法相较上述两种方法适应性更优,但不能科学阐述煤灰熔融过程中各成分演化规律以及灰熔融性的变化机理。
FactSage 软件法科学阐述了煤灰熔融过程中各成分演化规律以及灰熔融性的变化机理,创建了更可靠的模型,具有很高的精确度。FactSage 热力学平衡计算程序[12]基于最小Gibbs 函数的原理,并结合ChemSage 和FACT-Win 两套热力学软件包,包括上千个纯材料数据库,该软件能够在不同状态下模拟计算和准确评价煤灰的简化组成相图,对掌握灰熔融性的变化机理,对指导煤灰的资源利用、配煤掺烧等方面具有重要意义。
以296 种常见煤灰为样本,分别测定煤灰主要成分和流动温度,并采用现代理论方法,运用Fact-Sage 软件预测出煤灰主要成分与流动温度二者之间的关系。
1 实验部分
1.1 样本选取
选用296 种具有代表性的常见煤灰流动温度为原始数据,其中对实验室的26 种煤样进行干燥并制备成0.2 mm 分析样,根据GB/T 212—2008《煤的工业分析方法》中的缓慢灰化法制成灰分样品[13],并参照GB/T 219—2008《煤灰熔融性的测定方法》和GB/T 1574—2007《煤灰成分分析方法》两种标准方法测定煤灰进行流动温度和主要成分[3,14],计算煤灰酸碱比,并通过软件计算出煤灰流动温度TF,见表1,剩余270 种均从资料中搜集[15-17]。
1.2 统计分析
煤灰成分是影响灰熔融性的要素,是创建高准确性灰熔融性预测模型的基础,因此有必要客观的探究灰成分与熔融特性之间的相关性系数。相关性系数

表1 实验测定煤灰主要成分及部分特征温度

式中:R 为相关性系数;X 为煤灰主要成分质量分数;Y 为煤灰流动温度。|R|值越大,说明相关性越显著,回归线点越集中;相反,则说明回归线点的分布更为分散,|R|=1 表示它们完全正相关或负相关,R=0表示它们完全不相关。

表2 煤灰主要成分与流动温度之间的相关性系数

表3 煤灰主要成分质量分数的样本均值排序 %
综合表1 计算296 种煤灰成分与流动温度之间的相关性系数,见表2。为了建立更加优化的预测模型,探讨煤灰主要成分含量与流动温度之间的关系,以避免过高估计某些煤灰主要成分对煤灰熔融特征温度的影响。对煤灰主要成分含量与流动温度间的相关性系数按从大到小的顺序进行排列,综合对比表2 和表3 分析,除SiO2、TiO2、Na2O、Fe2O34 种煤灰成分外,其余煤灰主要成分含量越低,相关性就越弱。而对于这4 种煤灰成分,虽然SiO2含量最高,相关性却很弱;TiO2与Na2O 含量接近最低,但相关性位列中游;对于Fe2O3,因部分Fe2O3还原成FeO,所以抵消了Fe 元素对煤灰流动温度的影响。
2 回归方程研究
2.1 建立回归方程
根据不同煤灰流动温度的原始数据,煤灰的流动温度作为因变量,主要成分质量分数、酸碱比作为独立变量,进行多元线性拟合,并建立回归方程:
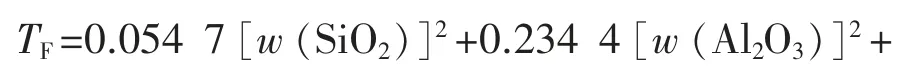

经计算,R=0.817,相关性比较显著,式(2)暂定为回归方程。
2.2 优化回归方程
由于296 种煤样在不同的实验室条件下测定,煤灰流动温度具有一定的偶然性,为尽可能地消除偶然因素的干扰,提高回归方程的精度,采用逐步回归法。建立回归方程,将上述原始数据代入回归方程进行检验,找到最大误差离散点,即计算值与实测值之差最大的点,并将其消除。
GB/T 219—2008《煤灰熔融性的测试方法》中规定流动温度的再现性临界值差超过80 ℃[5]即为错误数据。建立回归方程,原始数据代入回归方程进行检验,找到最大误差离散点,即计算值与实测值之差最大的点,并将其消除,反复进行上述操作,直至所有煤灰流动温度计算值与实测值之间相差均低于80 ℃,优化结束。最终得到回归方程

经计算得出R=0.949,具有很强的相关性。
2.3 检验回归方程
选用7 种煤灰,依据GB/T 1574—2007《煤灰成分分析方法》所述方法对煤灰主要成分进行测定,见表4,通过实测值来检验式(3)的准确性,将煤灰流动温度计算值与其实测值进行比较,见表5,计算差值全部小于80 ℃。可见,采用式(3)预测的结果准确度较高。
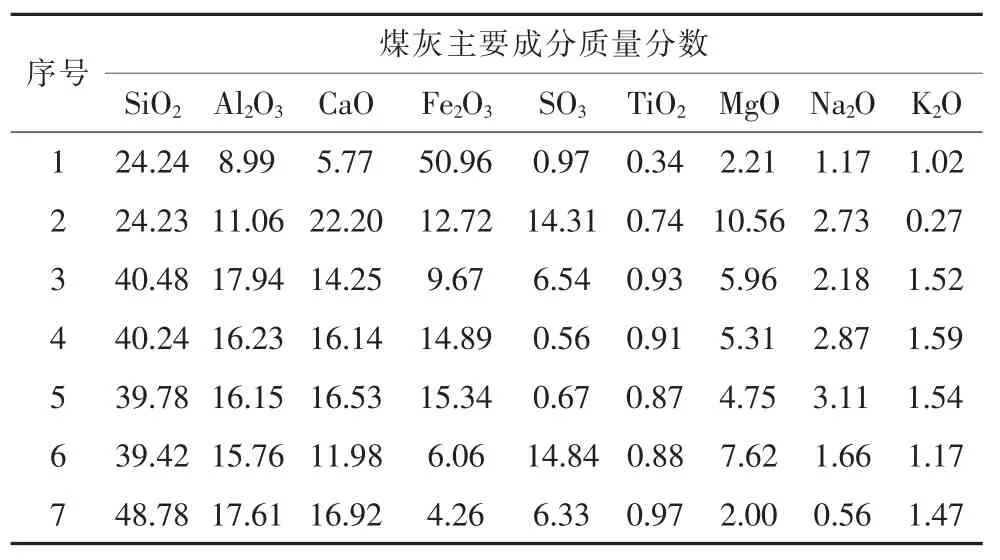
表4 实验测定煤灰主要成分质量分数 %

表5 流动温度实测值与计算值的偏差 ℃
3 结语
借助统计学对消除最大误差离散点的248 个煤灰流动温度原始数据,以煤灰的流动温度作为因变量,主要成分、酸碱比作为独立变量,利用FactSage软件,通过多元线性拟合准确建立煤灰主要成分与流动温度之间的回归方程,预测模型相关性系数达0.949。在探索研究方面,克服了实验的盲目性,提高了效率,节约了能源。
