纵·横·连：让数学思维向高阶漫溯

陈雪燕

【摘   要】数学是思维的体操，发展学生的高阶思维是数学教学的至真追求。教学应改变传统的教师不厌其烦讲述知识点和習题，却在学生思考和探索上“惜时如金”的做法，并通过“纵、横、连”来发展学生的数学高阶思维，即“凸显历程，让思维纵向延伸;增强开放，让思维横向拓宽;全面勾连，让思维走向高阶”。

【关键词】高阶思维;纵向延伸;横向拓宽;全面勾连

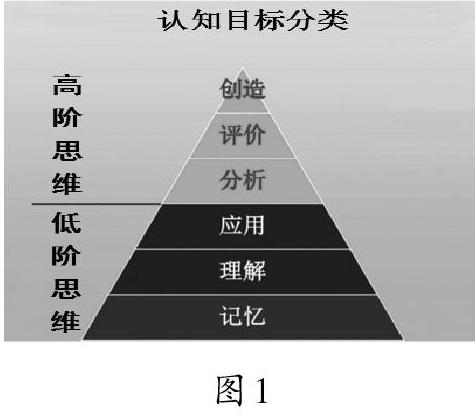
高阶思维是指发生在较高认知水平层次上的心智活动或认知能力。按照布鲁姆的“教育目标分类”理论，认知目标可以分为：记忆、理解和应用，分析、评价和创造。前者是已知状态下的学习，属于低阶思维;后者是未知状态下的学习，属于高阶思维（如图1）。结合小学数学学科自身的特点，笔者认为数学高阶思维是指数学情境中发生在较高认知水平层次上的综合性能力，包括分析解决问题能力、批判性思维能力和创造力等。传统教学中，教师不厌其烦地讲述知识点和习题，却在学生思考和探索上“惜时如金”，这种做法不利于培养学生的高阶思维。要发展学生的高阶思维，必须引导学生超越浅层、被动的学习状态，展开深度性、批判性、探索性和创造性的学习。本文将结合教学实践，谈谈让学生的思维走向高阶的思考和探索。

一、纵——凸显历程，让思维纵向延伸

为使学生的思维从低阶走向高阶，首先要让学生经历自主学习和操作的过程，做必要的知识和熟练规范技能方面的准备，在充分感知的基础上形成更高水平的思维。教学中教师应调动学生的多种感官，通过操作、游戏、讨论等活动，引发学生内部思维活动，经历从“基于直观动作的思维到基于具体形象的思维，再到基于抽象逻辑的思维”的递进过程，进而为高阶思维奠定基石。

（一）从“直观行动”思维到“具体形象”思维

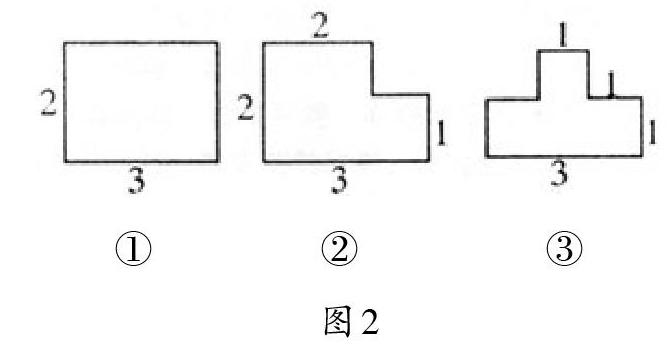
心理学家皮亚杰指出：“活动是认识的基础，智慧从动作开始。”化静为动，在教学中让学生通过动手、动脑、动口，在实践中发现问题、分析问题、解决问题，从“等待—解答”的状态走向“发现—创新”的状态。如在教学“长方形周长的计算”一课中，教师出示下面一题（如图2）：计算下面图形的周长。（单位：厘米）

学生能根据计算公式很快计算出图形①的周长，对于图形②③，教师让学生试做，然后教师指导学生用小棒摆出3个图形。通过摆小棒，学生惊奇地发现虽然3个图形的形状不同，但所用小棒的根数相同，平移图形②的两根小棒，图形②即转化为图形①，由此得出了计算图形②周长的简便方法。有了解决图形②的经验，计算图形③的周长就方便了。之后，教师根据学生的描述呈现图3，并让学生闭眼想象平移的过程。

在这个过程中，学生既进行了操作，又展开了观察想象，不仅发展了全息视域，加深了对知识的理解，更活跃了思维。当遇到类似的新问题时，学生便能快速准确地从大脑中检索并提取相关信息，形成关联，以解决问题。

（二）从“具体形象”思维到“抽象逻辑”思维

在成功尝试的基础上，教师又出示下题供学生研讨：若要在楼梯上铺地毯（如图4），必须知道楼梯的总长是多少，需测量哪些数据？地毯的长度是多少米？（出示图5）

由于学生刚才已掌握了平移方法，此时就不易受制于常规的解题思路，而是萌发出创造思维的火花，想象只要测出AB与BC的长即可求出地毯的总长度，即3+2=5（米）。可见，学生通过有效的操作，建立起丰富的表象，当面临新问题时，他们在头脑中进行知识的“再创造”，从而使数学思维向深处有序发展。

二、横——增强开放，让思维横向拓宽

只有发散思维与聚合思维两者协调发展，学生的思维水平才能形成和提高。开放性问题可以使学生的智慧得以启迪、潜能得以挖掘、创新思维得以激活，让学生的思维多维发散，向深度、广度、严密度发展，这样学生高阶思维能力的提升才能实现。

（一）问题开放，让思考层层递进

教师在教学中应该增强问题的开放性，诱导学生发散思维，围绕问题多角度去寻求答案，在此基础上进行概括，逐步形成规律性知识。

【案例1：什么情况下商中间有0】

教师出示“除数是一位数，商中间有0”的除法练习：（  ）÷8的商中间有0，（   ）里可填几，并思考“什么情况下商中间有0”。对于这样的题目，学生练习的积极性很高，相继在（   ）里填写了：808;8008;816;1616;824;2424;832;3232……

这些数，由被除数本身中间带0到不带0，由三位数到四位数，例子越举越多，共性也越来越明显，从而进一步概括出“什么情况下商中间有0”的规律。

（二）策略开放，让思考步步为营

即使有些只能有一个答案的问题，也应该鼓励学生从多思路、多途径、多角度去考虑，做到条条大路通罗马，这样才有利于开发学生的思维能力。

【案例2：多种巧妙方法解答等腰直角三角形面积】

例题：已知一个等腰直角三角形斜边长8厘米，求该三角形的面积（如图6）。

一开始大部分学生认为这题是不能做的，教师鼓励学生展开不同思路，结果貌似不能解答的题目，经过学生深入思考后，竟然得出了多种巧妙的解法。

解法1：用2个与图中完全一样的等腰直角三角形，可以拼成一个直角边为8厘米的大等腰直角三角形，它的面积是8×8÷2=32平方厘米，那么一个三角形的面积就是32÷2=16平方厘米。

解法2：用4个与图中完全一样的等腰直角三角形可以拼成一个边长为8厘米的正方形，拼成的正方形的面积是8×8=64平方厘米，那么一个三角形的面积就是64÷4=16平方厘米。

解法3：作斜边上的高，可知高是斜边的一半，正好是4厘米，直接算出三角形的面积是8×4÷2=16平方厘米。

解法4：用割补法，通过斜边上的高分割成两个完全一样的小等腰直角三角形，再拼合成边长是4厘米的正方形，正方形面积也就是原三角形的面积，即4×4=16平方厘米。

每一个学生都具有创新的潜质，关键是教师能否用恰当的方式去激发他们的才华。探索性、开放性强的内容，满足不同学生的个性化需求，唤醒学生头脑中最灵动的思维，敞亮他们的高阶思维。

三、连——全面勾连，让思维走向高阶

当面临新问题或解决较复杂的挑战性任务时，学生若能迅速检索、全面勾连旧知，并展开主动猜想、验证、批判，其高阶思维能力也定能悄然生成。

（一）旧知新用，积极推想

以旧知推想新知，大脑执行知识“同化”的过程，使新旧学习任务间能够顺利衔接。在个人学习时，我们要尽可能地寻找与新知识有相关性的旧知识，旁征博引，积极推想，通过旧知示证新知，使新知更易被理解、记忆及运用。

【案例3：最大最小问题勾连周长相等时的面积问题】

例题：把4、5、6、7填到□里，使得算式□□×□□的积最大。

生1：要想使算式的积最大，就要使这两个两位数尽可能大，所以这两个两位数的十位上的数分别是6和7，再通过计算比较75×64和74×65的积哪个大。75×64=4800，74×65=4810，因为4800<4810，所以74×65时，算式的积最大。

生2：75×64和74×65的积哪个大？我不是通過计算两个算式的积来判断的。75+64跟74+65它们的和是一样的，75与64差是11，74与65的差是9，相差小，积就大，所以选74×65。这就跟周长相等时长与宽相差越小，面积越大的道理一样。

随后，教师引导学生用生2的方法继续探究积最小的问题。

独特的想法使教学过程充满生机和活力。听完生2的回答，全班同学频频点头，表示赞许。显然，生2灵活利用旧知推想的想法更具创造性。在教学中可以用提问、测试、演示、讨论等方法帮助学生激活旧有知识，积极推想。

（二）类比模拟，大胆联想

著名数学教育家波利亚认为：“类比是一个伟大的引路人。”类比法是由此及彼或者是由彼及此的联想方法，具有启迪思维、举一反三的作用，是富有创造性的一种思维方法，教师要善于引导学生进行联想、类比，充分调动学生的想象力，让他们通过比较发现新旧知识之间的联系，将已学的知识或已掌握的方法迁移过来。其实，类比在小学数学教学中比比皆是，在推导梯形面积计算公式的时候就会类比联想到已学的三角形面积计算推导的方法。运用类比触发了灵感，突破原来的思维禁锢，收到化难为易、化生为熟的效果，实现了知识的正迁移，使问题得到创造性的解决。

总之，小学数学教学中要培养学生的高阶思维，需要教师着眼于学生的可持续发展，从传统教育“重知识学习而轻能力培养”“重机械记忆训练而轻操作应用”“重求同再现而轻求异创新”“重统一要求而轻个性发展”等弊病中解放出来，努力培养他们勤于思考、勇于提出问题的优良的学习品质，借问题促探索，借探索促发现，借发现促创新。优质的教学，不是让学生去消化教师的想法，而是激发学生的创造想法，让学生的思维去历险。

参考文献：

[1] 尹友胜.要把新知建立在旧知的基础之上[J].小学教学研究，2011（2）.

[2] 周莉.浅谈发展学生高阶思维的策略[J].小学教学参考，2018（2）.

（浙江省杭州市育海外国语学校   311122）