正交异性压电双材料反平面界面裂纹应力分析

赵慧娟，董安强，李俊林，谢秀峰

(太原科技大学应用科学学院,太原 030024)

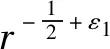
1 问题的描述与求解

如图1,正交异性压电双材料板含有长度为2a的反平面界面裂纹,xoy平面为正交异性界面,z轴为极化方向,受到无穷远处机械载荷σ0和面内电载荷D0作用。

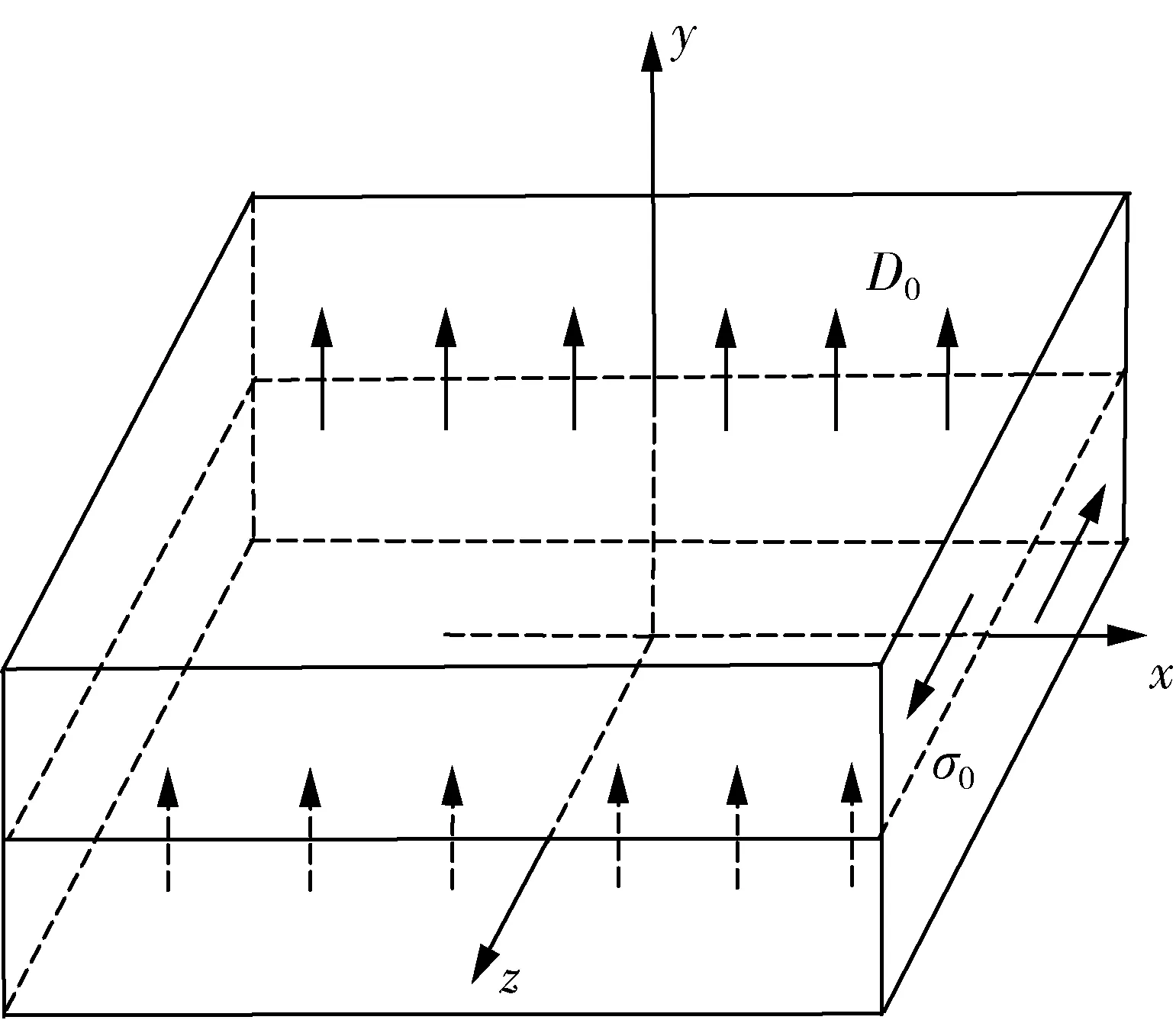
图1 正交异性压电双材料板

正交异性双材料反平面问题,其本构方程为：

(1)

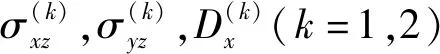
在不考虑体力和自由电荷的情况下,静态平衡方程和电静态下的Maxwell方程如下:

(2)

对反平面界面裂纹应力分析时,有:

将本构方程(1)代入静态Maxwell方程(2),有:

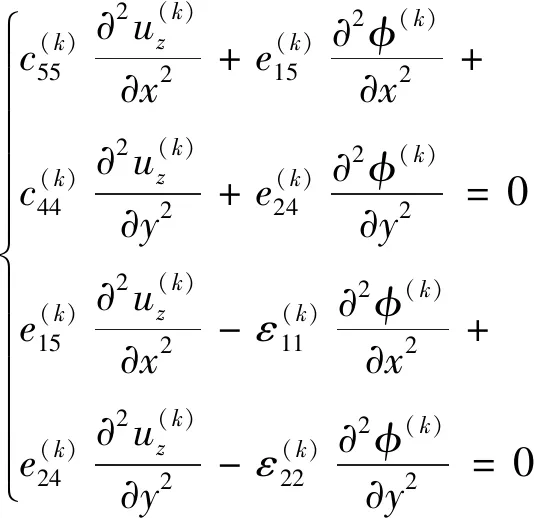
(3)

正交异性双材料的边界条件如下:

无穷远处边界条件:

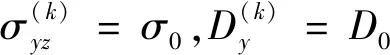
(4)

(5)

不可导通边界条件:

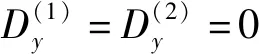
假设二：假设总是有一种标准的消费结构与产业结构的和谐状态存在着。现有的系统总是处于绝对不和谐与理想和谐状态之间的某一状态，对系统优化的目标是让系统向着理想的和谐状态转化。

(6)

根据复变函数理论,可知式(3)的位移、电势函数有如下实值解析解[7]:

(7)

将位移、电势函数表达式(7)带入本构方程(1)中,整理得:

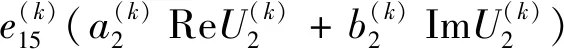
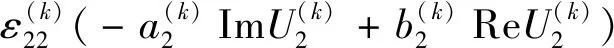
(8)

在反平面无穷远处对称机械载荷σ0,面内对称电载荷D0的共同作用下,选取如下函数:

(9)

在边界条件(4)时,式(9)的函数表达式整理为

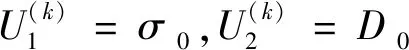
(10)

将式(10)代入式(8),整理后代入式(4),得到方程组,解方程组得:

在边界条件(5)时,式(9)的函数表达式整理为:

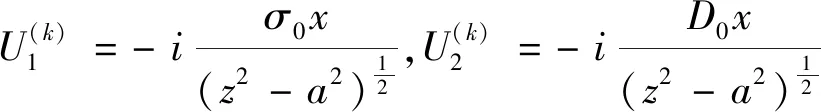
(11)

将式(11)代入式(8)整理后代入边界条件(5),将式(11)代入式(8)整理后代入边界条件(6),整理得到；

(12)

解方程组,解得：

定义反平面应力强度因子为：

则在裂纹尖端附近,即z→a时,

(13)

定义裂纹尖端应变强度因子:

将式(13)代入上式,则:

机械能应变释放率:

从上可知,裂纹机械能应变释放率由材料参数和载荷共同决定。

裂纹尖端附近的应力场和电位移场为:

2 数值算例分析

以正交各向异性压电材料为例,利用机械能应变释放率表达式,数值分析材料参数的差异、裂纹长度和外加机电载荷对机械能应变释放率的影响[8-11]。材料常数列于表1.其中ε0=8.854×10-12.

表1 各材料相关参数
Tab.1Relatedparametersofvariousmaterials

材料参数c44/(1010Nm-2)e24/(Cm-2)ε22/(Fm-1)KNBO3[8]7.4311.7780ε0KTP[9]5.9190.40311.47ε0

续表1

材料参数c44/(1010Nm-2)e24/(Cm-2)ε22/(Fm-1)PMN-PT[10]6.711.19640ε0KTA[11]5.80.6512.2ε0

以正交各向异性压电材料KNBO3、KTP、PMN-PT、KTA为例,利用机械能应变释放率表达式,数值分析材料参数的差异对机械能应变释放率的影响。

图2 Gm与a的关系

图3 Gm与σ0的关系

图4 Gm与D0的关系

由图2-图4可知,同样条件下,四种材料中,机械能应变释放率从小到大排列为:KNBO3、PMN-PT、KTP、KTA,即材料性能上KNBO3最有利于抑制裂纹扩展,KTA最不利于抑制裂纹扩展。正电场作用下的机械能应变释放率比负电场作用下的机械能应变释放率大,即正电场促进裂纹扩展,负电场抑制裂纹的扩展。分析材料参数的差异有利于工程上选择材料。

以正交各向异性压电材料KNBO3为例,利用机械能应变释放率表达式,数值分析裂纹长度和外加机电载荷对机械能应变释放率的影响。

图5 Gm与a的关系

如图5所示,在固定机电载荷作用下,机械能应变释放率与裂纹长度呈线性变化规律,即随着裂纹长度增加,机械能应变释放率增大。σ0、D0越大,直线斜率越大,裂纹长度对机械能应变释放率的影响越大,反之,裂纹长度对机械能应变释放率的影响越小。比较在正负电场作用下的机械能应变释放率与裂纹长度之间的变化曲线可知,正电场作用下的机械能应变释放率比负电场作用下的机械能应变释放率大,即裂纹长度对机械能应变释放率的影响在正电场比在负电场大。这与周振功[12]的结论一致。

图6呈现了机械能应变释放率随σ0的变化曲线。机械能应变释放率随着σ0的增大而增大,即应力总是促进裂纹扩展。从图中可知,裂纹长度a越大,Gm随σ0的变化越剧烈,即Gm随着σ0的增大变得越来越大;比较负电场下的Gm与σ0的关系曲线和正电场下的Gm与σ0的关系曲线可知,负电场作用下的机械能应变释放率小于相同正电场作用下的机械能应变释放率,即负电场载荷作用下的机械能应变释放率Gm随σ0的变化的影响小于正电场载荷作用下影响。

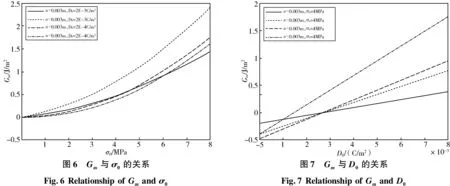
如图7显示了机械能应变释放率Gm余D0的关系,电载荷的大小与方向影响机械能应变释放率,且机械能应变释放率随着D0的增大而增大。正电场对机械能应变释放率的影响大于负电场,即正电场促进裂纹扩展,负电场抑制裂纹的扩展[13]。

3 结论

在反平面无穷远处机械载荷和面内电载荷作用下,利用复合函数法,研究了正交异性压电双材料反平面界面裂纹应力,得到应力强度因子、电位移强度因子、应力场、电位移场、能量释放率的表达式并通过数值算例,得到应力强度因子、电位移强度因子和能量释放率与力电载荷、裂纹长度有关;机械能应变释放率与材料参数的差异、裂纹长度、外加机电载荷之间的关系,裂纹长度越大,外加机电载荷越大,机械能应变释放率越大,正电场促进裂纹扩展,负电场抑制裂纹扩展。