超临界水喷放泄压因素的权重计算

周 涛，秦雪猛，朱亮宇，李子超，陈 杰

（1. 华北电力大学核科学与工程学院，北京 102206；2. 华北电力大学核热工安全与标准化研究所，北京 102206；3. 非能动核能安全技术北京市重点实验室，北京 102206；4. 东南大学，南京 211189）

在各种事故工况中，小破口失水事故在冷却剂丧失事故中发生频率较高，不仅会造成一回路降压问题，而且会在高压阶段引起堆芯长时间裸露而导致燃料元件升温损坏。目前，关于超临界水的事故程序研究多是其流动换热研究，对于超临界水的破口喷放的研究相对较少。刘亮[1]利用SCAC-CSR1000 程序计算分析了CSR1000 超临界水堆喷放过程质量流量的不规则变化特点；马栋梁[2]等人基于BP神经网络对超临界水传热系数进行了预测分析。本研究通过Small-break 自编程序，利用多因素方差分析方法，分析研究了小破口泄压因素的权重，对超临界水堆的安全运行有重要意义。

1 研究对象

为了研究超临界流体小破口喷放时，不同因素对破口处泄压速率的影响，本文选择了圆柱形喷放容器模型分析超临界流体小破口喷放后破口处压力的变化，圆柱形喷放容器如图1 所示。

图1中，喷放容器的高度为Zv；破口发生位置在Z0；容器内初始压强为P0，MPa；初始温度T0，℃；破口面积为A0，m2；h0为破口滞止焓，kJ/kg；容积为V，m3；D为容器直径，m。

图1 圆柱形喷放容器Fig.1 Cylindrical spray container

2 计算方法

2.1 容器守恒模型

忽略容器内的动能和势能对容器内压力的影响，圆柱形喷放容器能量守恒和质量守恒方程[3]如式（1）和式（2）所示：

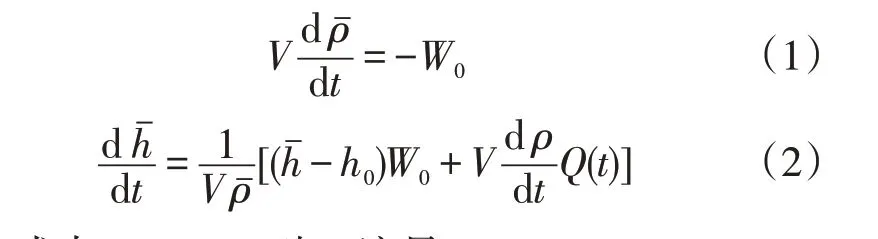
式中，W0——破口流量，kg/s；

V——容器的体积，m3；

t——时间，s；

Q(t)——单位时间传递冷却剂的热量，kJ/s。

2.2 临界流模型

临界流[4]是指当流体自系统中流出的速率不再受下游压力下降的影响时的流体。单相流也称声速流，此时，出口处的流量达到最大值。

选择Burnell[5]喷嘴两相临界流模型作为两相临界流模型，如式（3）所示：

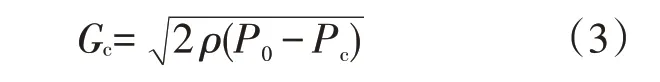
选择Bernoulli[6]的欠热两相非临界流模型作为两相非临界流模型，如式（4）所示：

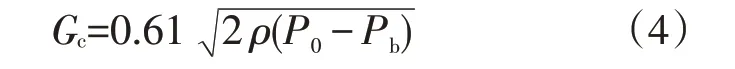
式中，Gc——质量流密度，kg/（m2.s）；

v1——气相比容，m3/kg；

P0——容器初始压力，MPa；

Pb——背压，MPa；

Pc——临界压力，MPa；

g——重力加速度，m/s2；

ρ——流体密度，kg/m3。

2.3 超临界水物性计算模型

超临界水在跨临界区域内会发生剧烈变化，水物性选择对超临界流体的计算非常重要，可以通过把热力学物性的源代码函数[7-9]嵌入本计算中解决水物性选择问题。

2.4 多因素方差分析计算模型

多因素方差分析的主要功能是分析因变量的总变异中不同来源的变异。多因素方差分析计算模型[10]为：

式中，F——统计量；

MSB——组间均方；

MSW——组内均方；

SSB——组间平方和；

SSW——组内平方和；

dfB——组间自由度，dfB=K-1；

K——组数；

dfW——组内自由度，dfW=K（n-1）；

n——每组水平数。

2.5 计算程序

2.5.1 计算流程

自编程序Small-break程序主要用来计算超临界水破口喷放过程中的破口压力、破口质量流量等参数变化。Small-break 计算流程如图2 所示。

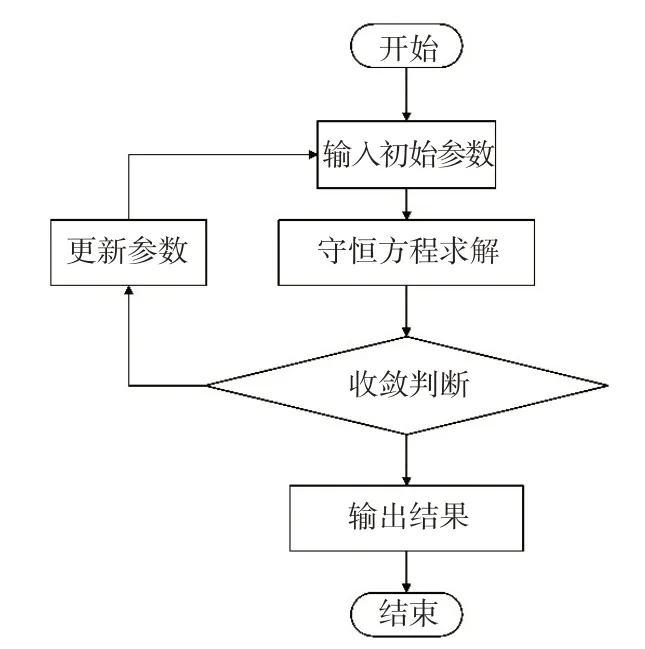
图2 Small-break计算流程Fig.2 Small-break calculation process

2.5.2 程序可靠性

Small-break 程序是华北电力大学核热工安全与标准化研究所周涛团队在超临界水堆安全分析程序TCAC-SA[11]的基础上优化编制而来，程序的可靠性已在相关文献[12]内得到验证。

3 计算结果及分析

3.1 初始压力的影响

设定破口初始温度为380 ℃，破口面积为80 cm2，容积大小为0.05 m3，初始压力分别为25 MPa、23 MPa、21 MPa 和19 MPa，对破口处压力进行计算，计算结果如图3所示。

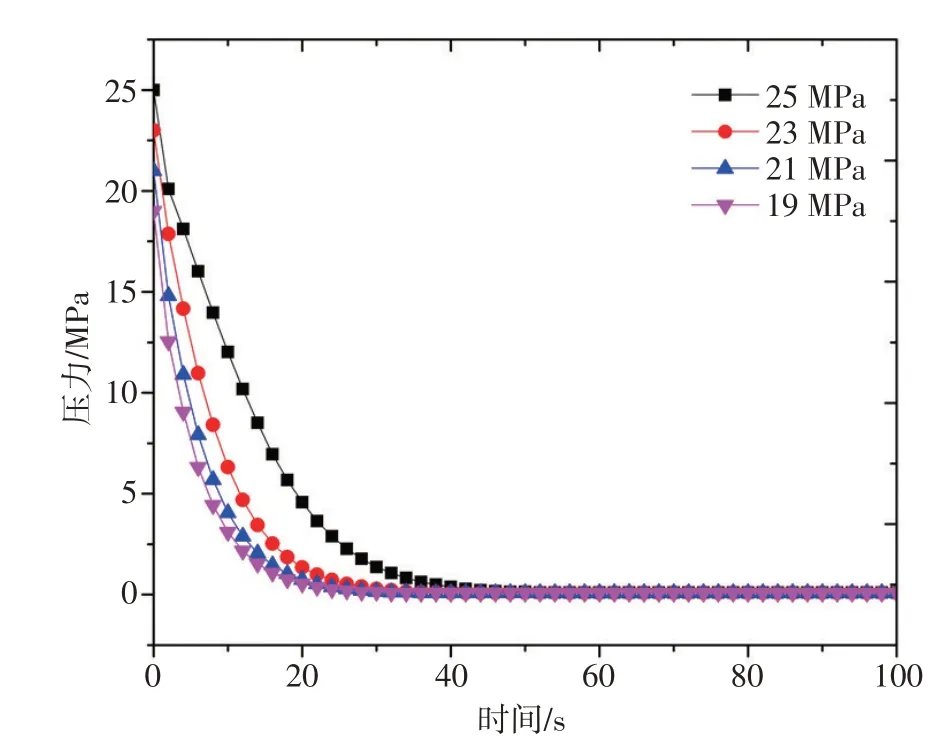
图3 破口处压力变化Fig.3 Pressure changes at the break

从图3可以看出，在一定范围内的不同初始压力下，破口泄压变化趋势相同，即先下降后趋于稳定。其中，初始压力越低，破口处泄压速率越快，主要原因是初始压力越大，离水饱和线越远，发生相变的时间越久，导致破口处泄压速率越慢。

3.2 初始温度的影响

设定破口初始压力为25 MPa，破口面积为80 cm2，容积为0.05 m3，初始温度分别为380 ℃、370 ℃、360 ℃和350 ℃，对破口处压力进行计算，计算结果如图4所示。

由图4 可以看出，在不同初始温度下，破口发生0～10 s 时，初始温度越高，破口处泄压速率越慢；破口发生10～40 s 内，泄压速率与前10 s 情况相反，初始温度越高，破处泄压速率越快。主要原因是，在0～10 s 内，初始温度越高，离水饱和线越远，相变时间越久，但在10～40 s 内，相变已经发生，进而后期发生逆转。

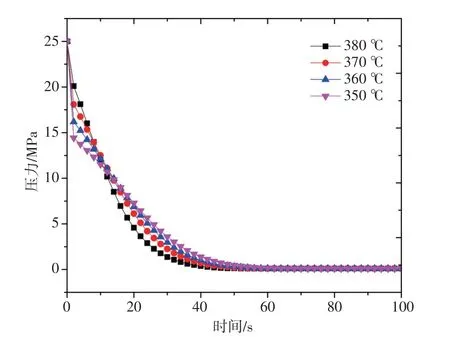
图4 破口处压力变化Fig.4 Pressure changes at the break

3.3 破口面积的影响

设定破口初始压力为25 MPa，初始温度为380 ℃，容积0.05 m3，破口面积分别为100 cm2、80 cm2、60 cm2和40 cm2，对破口处压力和质量流量进行计算，计算结果如图5所示。

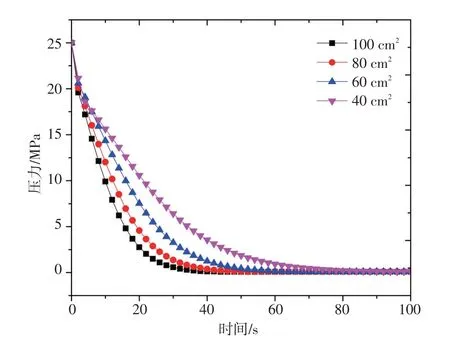
图5 破口处压力变化Fig.5 Pressure changes at the break

从图5 可以看出，在不同初始破口面积下，破口泄压变化趋势相同，先下降后趋于稳定。其中，初始破口面积越大，破口处泄压速率越快，主要原因是破口面积越大，破口压力边界的压力损失越严重。

3.4 容器体积的影响

设定破口初始压力为25 MPa，初始温度为380 ℃，破口面积为80 cm2，容积大小分别为0.03 m3、0.05 m3、0.07 m3和0.09 m3，对破口处压力进行计算，计算结果如图6所示。

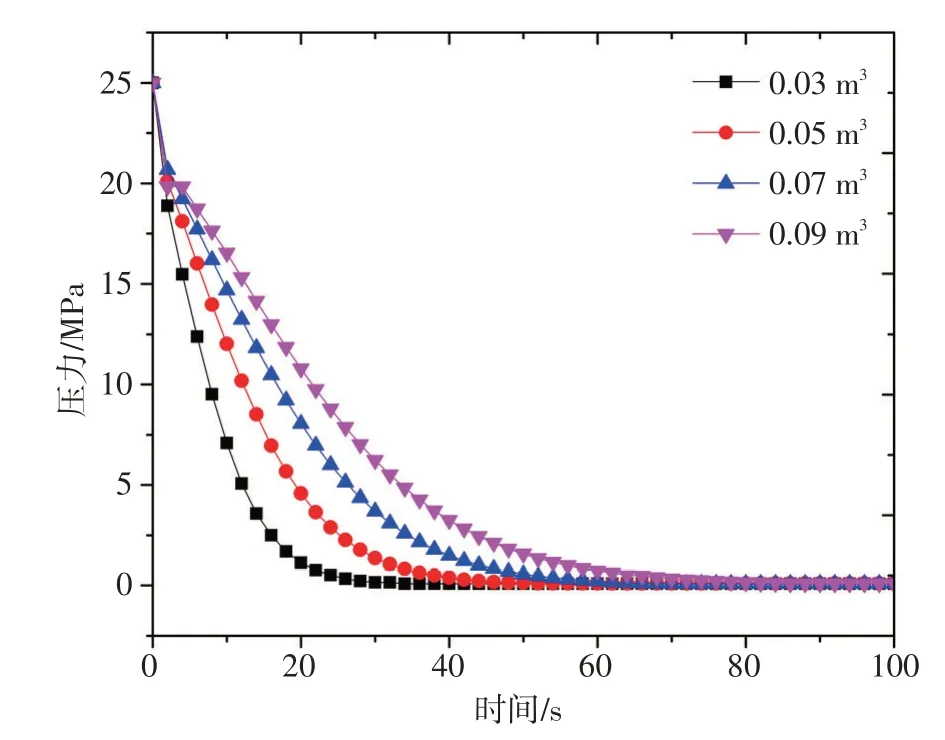
图6 破口处压力变化Fig.6 Pressure changes at the break

从图6 可以看出，在不同初始容积体积下，破口泄压变化趋势相同，先下降后趋于稳定。其中，初始容积越大，破口处泄压速率越快，主要原因是初始容积越大，导致容器内压力变化越快，达到平衡的时间就越短。

3.5 破口泄压权重分析

根据多元因素方差分析模型，将初始压力、初始温度、初始破口面积、初始容积大小作为影响超临界水喷放泄压的因素，每个因素取4 个水平，建立4 因素4 水平的正交实验表。正交表数据见表1。

对表1的正交表数据进行处理分析，计算后得到破口面积、容积、初始压力和初始温度的F统计值分别为8.58、7.89、4.17、1.21。分析各影响因素权重占比情况如图7所示。

由图7 可知，各因素的F 统计值都大于1，说明4个因素对破口处压力都具有显著影响。破口面积、容积体积、初始压力和初始温度的权重占比分别为39%、36%、19%、6%。

表1 正交表数据Table 1 Orthogonal table data

图7 各影响因素权重占比Fig.7 The weight of each influencing factor

4 结论

本文通过Small-break 程序计算超临界流体喷放过程各参数变化，并利用多因素方差分析方法对破口喷放的各因素进行权重分析，得到了各因素的影响程度。

（1）在19～25 MPa 范围内的超临界流体初始压力越低，破口处泄压速率越快；

（2）在破口发生前期，初始温度越高，破口处泄压速率越慢，但破口发生后期其泄压速率反而越快；

（3）破口面积越大，泄压速率越快，但容积越大，泄压速率越慢；

（4）泄压因素的权重占比从高到低依次为破口面积、容积、初始压力和初始温度。