核反应堆物理热工耦合的瞬态分析方法研究

王昆鹏，许 超，李聪新，刘宇生，温丽晶，王宏凯，刘 健

（生态环境部核与辐射安全中心，北京 100082）

核反应堆瞬态分析是核反应堆安全及事故分析的基础，一座核反应堆能否安全运行的关键是能否成功控制反应堆功率在各种情况下的安全运行[1]。世界上3 次严重的核事故发生后，人们对核反应堆的安全性提出了更高的要求，对核反应堆安全分析的要求也更加严格[2]。而核事故的发生往往伴随剧烈的功率变化，所以，从安全的角度出发，核反应堆的设计和事故分析往往都希望得到最接近堆芯实际功率的功率值，从而准确地模拟反应堆功率的空间分布及瞬态变化[3]。另一方面，堆芯功率的变化又会影响堆芯燃料及冷却剂等材料的温度与密度参量，这些参量变化带来的反馈作用又反过来影响中子通量密度，因此，考虑堆芯物理和热工的耦合计算是反应堆瞬态分析的重点[4]。

1 物理热工耦合的基本方式

核反应堆的瞬态分析需要进行堆芯物理和一回路系统的热工耦合计算。物理热工耦合的方法有很多种[5-7]，根据堆芯和一回路系统耦合点的不同，主要分为3类。

第一种耦合方式为内部耦合，如图1 所示。采用该耦合方式进行热工水力计算时，计算包括堆芯在内的所有一回路设备，而中子学计算只提供堆芯部分的功率分布。此种耦合方式的特点是中子程序和热工程序互为边界条件，计算结果为对方的初始条件，因此，该耦合方法便于利用已有中子学程序和系统程序开展物理热工耦合计算。

第二种耦合方式为外部耦合，如图2 所示。在该耦合方式中，中子程序计算包括控制棒和堆芯流体在内的中子计算；系统程序仅包括除了压力容器之外的热工水力计算。因此，进行物理热工耦合计算时，需要对中子程序进行改进，增加热工反馈模块。

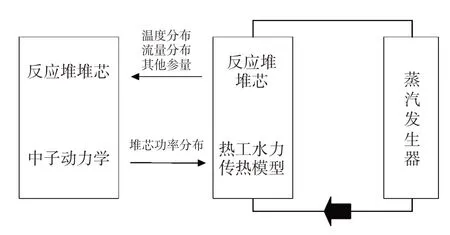
图1 内部物理热工耦合Fig.1 Internal physical thermal coupling

图2 外部物理热工耦合Fig.2 External physical thermal coupling

第三种耦合方式为混合耦合，即第一种方式和第二种方式的结合。在中子计算的同时进行了堆芯部分的热工水力计算，而系统程序也计算了包括堆芯在内的整个一回路的热工水力，显然利用此方法进行计算的结果更加精确，但计算时间较长。

物理热工耦合的计算模型又有很多种，主要取决于中子动力学和热工水力的计算方法。中子动力学的计算方法主要基于点堆动力学、中子扩散理论动力学和中子输运理论动力学，热工水力的计算方法包括点模型、单通道、子通道、系统程序等，国外主要核电发展国家关于物理热工耦合的研究见表1，日本、墨西哥等国基于点堆模型开展了关于快堆、行波堆等堆型的研究工作[8]；德国、法国和美国都基于中子扩散动力学和子通道程序耦合的方式开展了气冷快堆、VVER 反应堆的瞬态研究[9]；美国和德国基于中子输运动力学和计算流体动力学（CFD）程序开展了相关前瞻性的研究工作；我国也进行了类似的研究工作。

表1 国外物理热工耦合的常见方法Table 1 Common methods of physical thermal coupling abroad

物理热工耦合的计算方式包括，一步耦合（显式耦合，如图3 所示）和多步耦合（隐式耦合，如图4 所示）。图3 中，假定TN时刻的堆芯功率分布和热工-水力状态已经求出，采用一次通过的过程得到TN+1时刻的结果。其优点是整个过程只进行了一次中子学计算和一次热工水力计算，没有进行迭代，节省时间；缺点是时间步长不能太长，否则计算结果失真度很大。隐式耦合，在中子学计算和热工-水力计算之间进行迭代计算，直到中子学计算和热工水力计算收敛为止。这种耦合的方式计算结果较为准确，然而计算时间较长。

图3 一步耦合Fig.3 One-step coupling

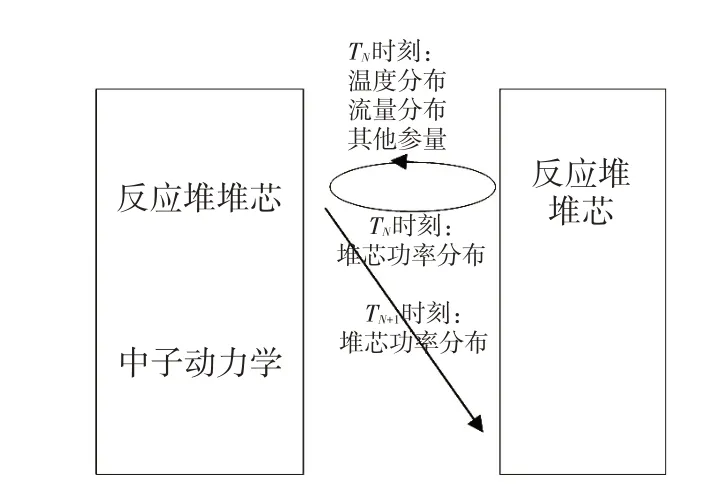
图4 多步耦合Fig.4 Multi-step coupling

2 基于点堆动力学的物理热工耦合

在早期，研究人员主要采用简单的“点堆”动力学近似模型[10，11]，对反应堆瞬态动力学进行研究。该方法的特点是将整个反应堆堆芯功率假定为一个平均值，该值随时间进行变化。

点堆动力学的方程为：

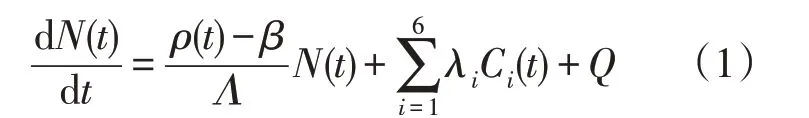
和

式中，N(t)——中子密度；

Ci(t)——第i组缓发中子先驱核浓度；

λi——第i 组缓发中子先驱核的衰变常数；

βi——第i组缓发中子份额；

Λ——中子代时间；

β——缓发中子份额；

Q——源项；

ρ(t)——t时刻的反应性。

ρ(t)的取值取决于反应堆状态，即燃料棒温度、冷却剂温度、冷却剂密度、空泡份额等，反应性根据上述条件的变化而变化，反应性的变化会影响功率的变化。因此，采用点堆动力学模型进行物理热工耦合计算时，应在每个时间步上对反应性进行修正，其计算公式为：

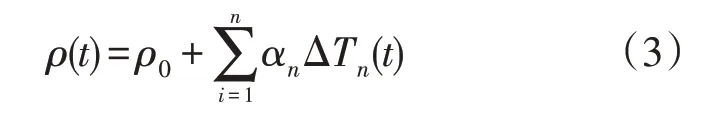
式中， ρ0——初始时刻引入的反应性；

αn——变量Tn的反应性反馈系数；

ΔTn(t)——t时刻变量Tn的变化量。

针对不同的反应堆，变量Tn都有对应的计算公式，但是，计算公式中都包含功率。基于点堆动力学的物理热工反馈计算模型如图5所示。

基于点堆动力学的物理热工耦合方法计算效率较高，一般能实现对反应堆瞬态的快速分析，点堆动力学方程刚性较强,常采用全隐式龙格库塔方法求解[12]。

3 基于时空中子动力学的物理热工耦合

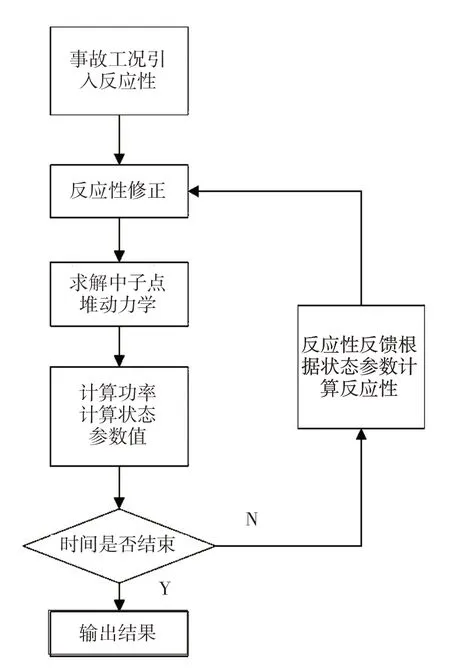
图5 基于点堆动力学的物理热工耦合计算流程Fig.5 Neutronic thermal-hydraulic coupling calculation flow based on point reactor model

点堆模型采用集总参数的方法，不能描述与空间有关的动力学效应，仅能对小型紧耦合系统且偏离临界状态不远的问题给出较满意的计算结果；而像大型商用动力堆这类可能发生中子通量空间分布显著畸变的情况，“点堆”模型已远远不够。

近年来，研究人员已开始以多群、多维、节块扩散模型作为首选进行反应堆的安全事故分析和仿真模拟[13]。节块扩散模型可以提供堆芯功率空间分布，提高了安全分析的准确度，使对大型商用堆的分析达到了精度要求。但是，随着对一些特殊问题研究的不断深入，如具有体积小、高泄漏和含有强烈吸收体等特点的空间堆，体积小、冷却剂中又含有大量空泡的溶液堆，以及其他一些由非对称布置的控制棒移动诱导的反应堆瞬态问题，对反应堆安全分析提出了新的课题要求，扩散模型已不能给出精确的结果，从而需要有更高精度的模拟计算。所以，随着反应堆技术的发展，公众对反应堆的安全性和经济性有了更高的追求，使研究人员不再满足基于扩散理论和利用低维的方法解决反应堆动力学问题，而越来越趋向基于输运理论的三维时空动力学方程的求解[14]，以期获得对堆芯物理瞬态过程更精确的变化分析结果。并且核安全要求的是完整的堆芯瞬态分析，反应堆的动力学受制于中子物理过程和堆芯多种状况的耦合，事故安全反馈效应是必须考虑的。

描述核系统动力学特性的方程组属于刚性初值问题，求解时，要求对时间变量的离散问题具有良好的稳定性和收敛性。对时空动力学方程组中的时间变量的处理有两类方法，即间接近似格式和直接的差分格式。而对时间变量的离散处理通常采用无条件稳定的全隐式向后差分格式。用全隐式向后差分格式处理以下常微分初值问题：

式中，n——时间步；

tn+1——第n+1步的时间；

tn——第n 步的时间；

Δtn+1——时间步长，Δtn+1=tn+1-tn；

t——时间。

关于时空动力学的研究，已经有了很多研究成果，主要集中在对时间变量的处理，具体包括一些数值处理方法和相应的瞬态计算程序。而各类时间变量离散方法中，因子分解法是将时空相关的中子通量密度直接分解为一个随时间变化很缓慢的形状函数和一个仅随时间变化的幅函数，可以根据各自对时间的依赖性采取不同的时间步长，以大大减少计算时间，满足三维时空中子动力学计算对速度的高要求。同时，因子分解在形式上是严格的，并不存在近似，所以，具有和直接离散方法相同的精度。

如式（6）对时空相关的中子通量直接进行了因式分解，代入三维时空动力学方程中可以得到有关形状函数的方程：

式中，ψ( r,E,Ω,t )——描述中子通量密度的形状函数；

T( t )——描述中子通量密度的幅函数；

Φ——中子通量密度；

r——中子在空间中的位置；

E——中子能量；

Ω——描述中子运动方向的向量。

绝热近似方法完全忽略了式（6）中形状函数和幅函数的时间导数项，并忽略了先驱核形状分布的时间延迟，不区分缓发中子源和瞬发中子源项。

准静态方法[15，16]认为形状函数随时间变化很缓慢，完全忽略式（6）中形状函数的时间导数项，其他保持不变，时间变量t 在形状函数方程中只呈现为一个参数，即：

改进准静态方法（Improved Quasistatic Method，IQS）则保留式（8）形状函数的时间导数项，采用全隐式向后差分格式进行时间离散，即：

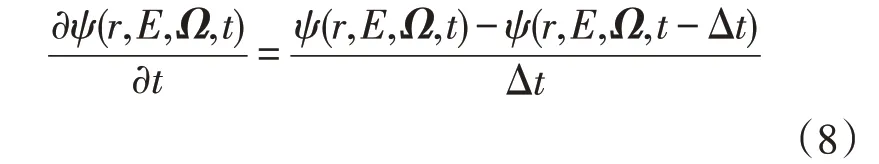
比较3 种方法可知，绝热法作了太多近似，精度有待提高，该法已不再使用；准静态方法可以较好地描述渐近的瞬态变化，然而对于较快的瞬态变化，特别是阶跃变化引起的瞬跳变化则不能给出精确解；而改进准静态方法考虑了形状函数随时间的变化，不论是瞬跳还是渐进的瞬态过程结果，都较准确。

IQS具体到瞬态时间的离散，形状函数和幅函数对时间变量不同程度的依赖性提供了利用不同时间间隔的机会。形状函数只有在需要时才进行更新计算，计算时间之间的间隔选取比幅函数的时间间隔大得多，在不降低解的精度下，使计算时间大幅度减小。可以按照不同的时间间隔划分分别求解形状函数和幅函数，从而大大减少计算时间，提高了计算效率，解决了直接用离散方法计算速度过慢的问题。同时，规划时间步长和各时间步长等级之间的变化成为改进准静态方法的重要内容之一。

基于时空中子动力学的物理热工耦合，反应性截面是物理热工反馈的关键。因瞬态计算过程分析的时间足够短，通常以秒为单位，在这样的时间尺度下可以认为燃料的燃耗是恒定不变的，反应堆中的毒物也不随时间发生变化，各动力学参数变化非常缓慢，这样各计算区域的截面仅取决于燃料及冷却剂的温度和密度。另外，对于控制棒区，还要考虑控制棒是否插入。因此，完整的截面群常数计算公式可以表示为：

式中，f1(Bu)——有关燃耗的多项式；

f2(v)——有关温度的多项式；

f3(p)——有关相对功率密度的多项式；

f4(Cr)——控制棒的影响变化量。

各参数的计算公式和具体堆型有关，由具体堆型确定。

基于三维时空中子动力学模型的物理热工耦合计算流程如图6所示，而反应堆的状态需要热工程序进行计算，从而获得反应堆燃料的温度分布、冷却剂的温度和密度分布参数，可以利用式（9）计算出反应性截面，从而进行中子动力学的计算。

图6 基于时空中子动力学的物理热工耦合计算流程Fig.6 Neutronic thermal-hydraulic coupling calculation flow based on space-time kinetic model

4 物理热工耦合的发展趋势

鉴于计算能力的迅速提高以及新的反应堆广泛采用MOX 燃料，设计燃耗深度也在不断提高，燃料的各向异性非常显著。因此，采用更精确的模型，即中子学计算采用蒙特卡罗方法求解中子输运方程[6,17]；热工水力计算采用子通道模型，甚至采用计算流体动力学（CFD）方法进行物理热工耦合计算，都是未来的研究趋势。另一方面，提高原有输运程序的计算速度、改进热工模型、开发人机接口界面、开发通用堆型的物理热工耦合程序也是未来的研究热点方向。

5 结论

本文总结了反应堆瞬态分析中物理热工耦合的主要方法，分析了各种耦合方法的优缺点，结论如下：

（1）反应堆堆芯和一回路系统的耦合方式可以分为内部耦合、外部耦合和混合耦合3种方式，其中内部耦合方式便于利用已有程序；外部耦合方式便于系统程序建立计算模型；混合耦合方式精度最高，但计算效率较低；

（2）物理热工耦合的方式根据同一个时间步长内是否迭代可以分为一步法和多步法，其中，一步法计算速度较快，但计算步长不能太大；多步法计算精度较高，但效率较低；

（3）根据物理热工模型维数的不同，可以划分为基于点堆动力学的耦合方法和基于时空中子动力学的耦合方法。早期受制于计算条件，一般采用基于点堆动力学的耦合方法。而时空中子动力学耦合模型，尤其是基于蒙特卡罗方法的时空中子动力学模型因广泛的堆芯适应性及高计算精度，并且可获得各时间步长下堆芯三维功率、温度等参数的分布，是未来物理热工耦合模型的发展方向。