高分辨率光学/SAR卫星几何辐射定标研究进展

张 过，蒋永华，李立涛，邓明军，赵瑞山

1. 武汉大学测绘遥感信息工程国家重点实验室，湖北 武汉 430079; 2. 武汉大学遥感信息工程学院，湖北 武汉 430079; 3. 湖北师范大学城市与环境学院，湖北 黄石 435002; 4. 湘潭大学信息工程学院，湖南 湘潭 411105; 5. 辽宁工程技术大学测绘与地理科学学院，辽宁 阜新 123000

星载光学、SAR是获取地理空间信息的重要手段。近年来随着航天技术的不断发展，国内外光学、SAR遥感卫星朝着高空间分辨率、高定位精度、高敏捷机动能力等方向发展，主要体现在：①在空间分辨率方面，国内外亚米级甚高分辨率卫星已经得到大规模使用，美国于2014年发射的WorldView-3卫星全色分辨率已经达到0.31 m[1]，成为当前最高分辨率的商业卫星；②在定位精度方面，卫星影像的定位精度由早期的千米量级[2]，逐渐提升至SPOT 5的50 m[3]、IKONOS的12 m[4]，直至当前WorldView、GeoEye的3 m左右[5]；③在敏捷机动方面，美国最早于1999年发射敏捷卫星IKONOS-2，此后美国陆续发射了QuickBird、WorldView等敏捷卫星[6]，2011—2012年法国发射的Pleiades系列卫星展现出了更为优秀的敏捷机动能力[7]。

在轨几何辐射定标是通过地面手段消除星上成像系统误差，是提升星载光学、星载SAR几何辐射质量的主要手段。

在轨几何辐射定标主要由场地定标、交叉定桥和天场定标3类。场地定标是指利用几何定标场或辐射定标场进行成像系统参数标定；交叉标定是指利用已经标定好的卫星影像做为基准，对待定标影像进行成像系统参数标定，作为基准的影像和待定标影像可以是同一颗卫星影像或不同卫星影像。

1 星载光学几何定标基本原理与研究进展

1.1 外方位元素定标

光学卫星在轨成像过程中相机主光轴在物方坐标系下的位置指向主要由相机安装、卫星位置和卫星姿态确定，即卫星摄影测量中的外方位元素。外方位元素定标是为了消除卫星载荷安装、姿轨测量系统误差，提升光学卫星绝对定位精度[8]。

1.1.1 场地外方位元素定标

线阵推扫光学卫星单次曝光成像仅获取相机视场内的一行图像，而随着卫星与地面的相对运动，相机随卫星运动扫描地面不同区域最终形成二维图像。线阵推扫光学卫星的严密几何定位模型可构建如下

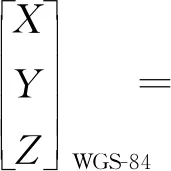
(1)

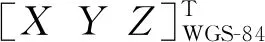
目前事后定轨精度可达厘米级，因此可认为轨道数据不存在误差。外方位元素定标主要考虑相机安装误差、星敏安装误差和姿态测量系统误差，可以采用偏置矩阵RU进行统一补偿，RU可定义为

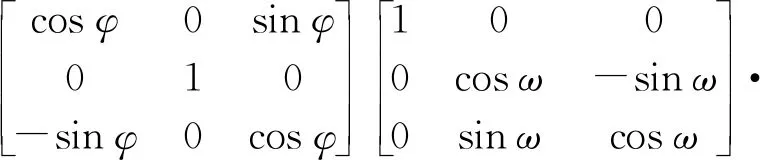
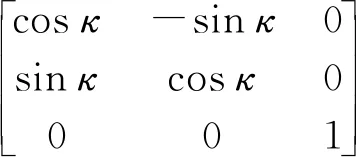
(2)

φ、ω、κ作为未知数，利用不少于两个平高控制点(x,y,X,Y,Z)i，基于最小二乘原理求解式(2)中φ、ω、κ即可完成外方位元素定标。

1.1.2 无场外方位元素定标

式(1)以滚动角误差为例，OS为真实成像光线，OS’为带误差成像光线，ω为垂轨向成像角(包含成像侧摆角、探元视场角等)，Δω为滚动角误差，H为卫星高度。则可得垂轨向定位误差ΔY为

Y=H[tan(ω)-tan(ω+Δω)]

(3)

图1 轨道坐标空间滚动角误差对几何定位的影响分析Fig.1 Analysis on the influence of orbital coordinate space rolling angle errors on geometric positioning

考虑Δω通常为小角度，式(3)可作如下近似

上式表明，在轨道坐标空间下，滚动角误差引起的定位误差方向仍然由Δω的正负确定。然而，Δω的正负取值定义于轨道坐标系，如图2所示，当卫星整体平台作偏航180°旋转时，则相当于Δω符号取反。滚动角误差引起的几何定位误差大小保持不变而方向相反。

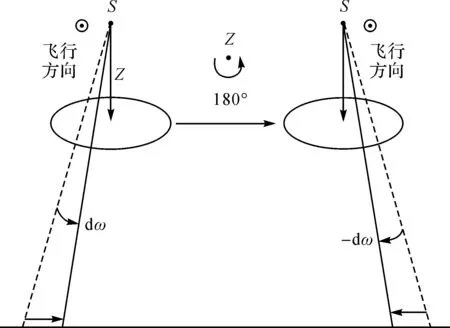
图2 物方空间下姿态误差引起的几何定位误差Fig.2 Geometric positioning errors caused by attitude errors in object space

根据姿态误差在轨道空间的这一特性，利用卫星敏捷快速机动以在短时间内两次扫描同一区域，保持两次扫描的卫星侧摆、俯仰角相近而偏航角相差180°，则可根据两次影像几何定位误差大小相近、方向相反的特点实现外方位元素定标。

从两张偏航角相差180°的影像上获取同名点对(x1,y1)和(xr,yr)，基于几何定位模型分别求取两点的物方坐标

(4)

式中,f代表严密几何模型。式(4)中，为降低高程投影差的影响，几何定位利用全球SRTM-DEM数据获取高程。根据姿态误差上述分析特性可知两次成像中同名点位置符合式(5)

(5)

因此，同名点对(x1,y1)和(xr,yr)的真实地面坐标(忽略高程影响)为

(6)

利用外方位元素误差大小相近、反向相反的特性可以间接获取用于外方位元素定标的控制点。当从两张影像上获取两对或更多同名点，则可解求式(2)所示偏置矩阵。

1.2 内方位元素定标

内方位元素定标是为了消除主点、主距、镜头畸变等内方位元素误差，精确确定成像光线在相机坐标系中的真实指向，保障光学卫星相对定位精度。

1.2.1 场地内方位元素定标

从高精度定位的角度，重要的并不是剥离各项内方位元素误差并恢复它们的真值，而是恢复成像光线在相机坐标系下的真实指向。因此，以指向角作为内方位元素表示模型，不再区分各种内方位元素误差项。令

考虑存在主点平移(Δx0Δy0)、主距误差Δf、探元尺寸误差sy、CCD旋转误差θ及径向畸变(k1k2)、偏心畸变(p1p2)的线阵CCD指向角为

(7)

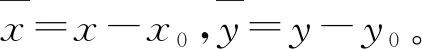
(8)

1.2.2 交叉内方位元素定标

图3为A、B卫星分别对同一地物点S成像，且分别成像于CCD线阵上的像元p0和p1处。

假定A、B卫星的成像几何参数(包括测量的轨道、姿态和相机内方位元素)准确无误，且地物点S高程已知，则根据几何定位模型进行计算，p0和p1都应该定位于S所处的地面坐标

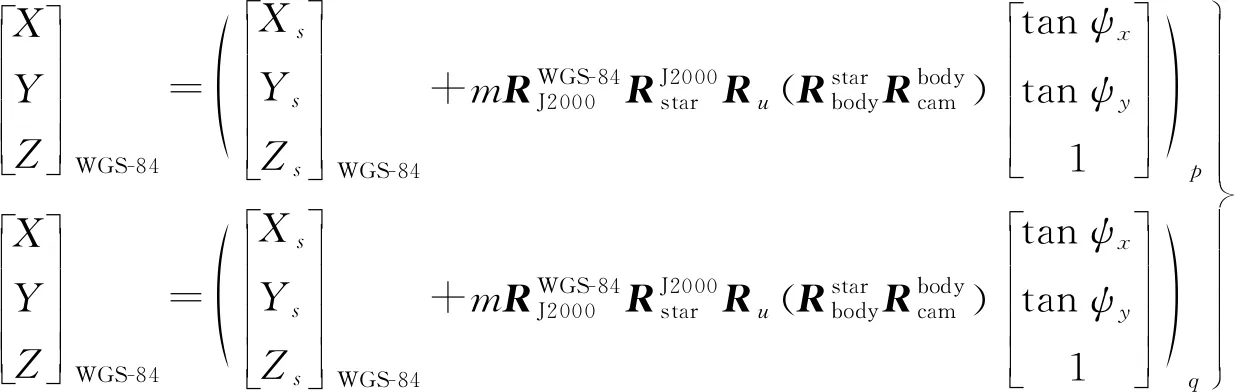
(9)

但由于高程误差、外内方位元素误差的影响，式(9)通常并不能成立。图3中高程误差对同名点的交会影响近似为

ΔS=Δh(tanθ1-tanθ0)

(10)

式中，θ0和θ1为前后两次成像的姿态角；Δh为高程误差。显然，Δh取决于几何定位时采用的地形数据(如全球公开的SRTM-DEM数据)，因此，当θ0和θ1足够接近，即卫星以非常相近的姿态角连续两次拍摄同一区域时，则可消除高程误差对同名点交会的影响。进一步由分析可知，轨道误差引起的定位误差为平移误差，而姿态误差引起的定位误差为平移误差和旋转误差，因此可以采用式(2)所示偏置矩阵Ru同时消除轨道、姿态误差对同名点交会的影响；假定A星已经完成内方位元素定标， 则可采用式(8)所示内方位元素模型标定B星

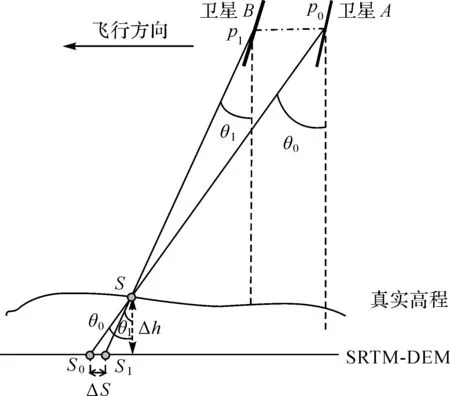
图3 物方空间下姿态误差引起的几何定位误差Fig.3 Geometric positioning errors caused by attitude errors in object space

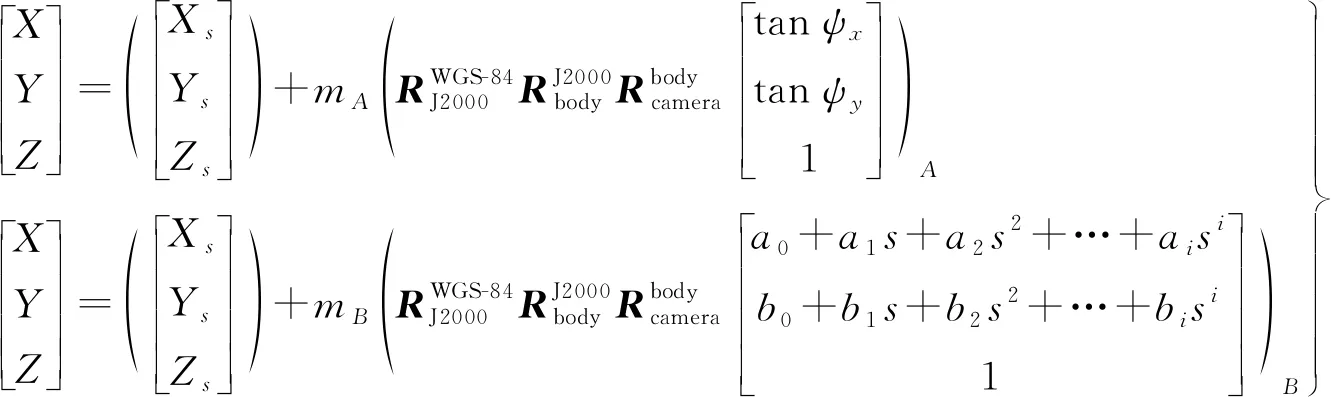
(11)

为进一步保障B星内方位元素定标精度，将B星相邻CCD线阵上同名点应交会于地面同一位置作为几何约束，加入定标平差模型。采用两类未知数迭代求解思路，基于同名点交会约束的求解内方位元素。

1.2.3 无场内方位元素定标

图3中当卫星A和卫星B为同一颗卫星，且以相近成像角拍摄同一区域，则构成卫星无场内方位元素定标条件。此时，同名点交会误差反映了卫星两个时相影像的外方位元素误差和相机内方位元素误差。同样采用式(2)偏置矩阵、式(8)多项式模型来消除外内方位元素误差影响

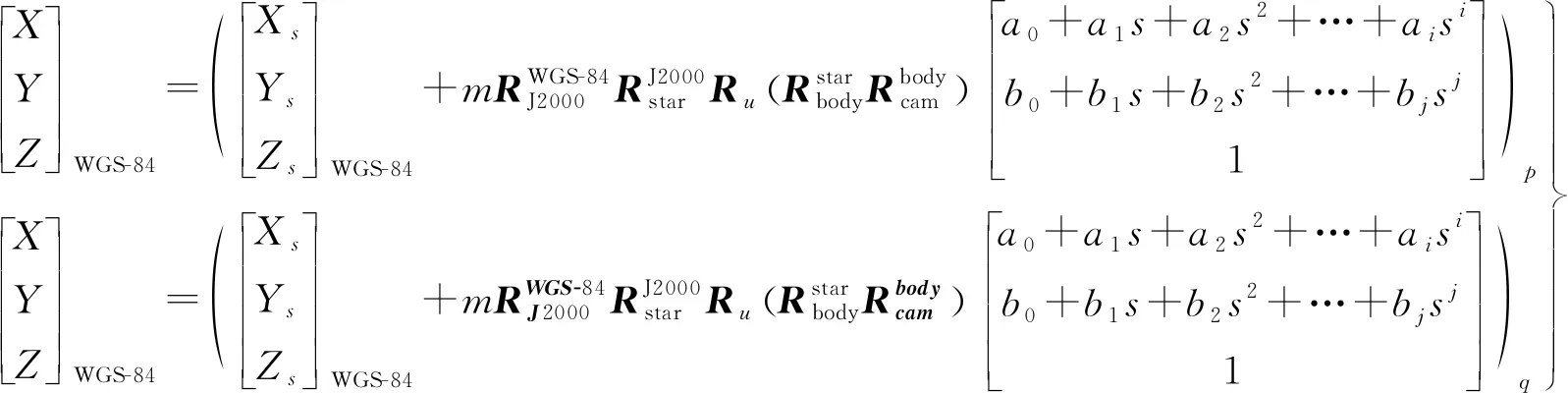
(12)

无场内定标采用成像角度相近的多时相影像实现。而由于成像角度相近，立体交会条件弱，高程求解不稳定，同名点的三维坐标(X,Y,Z)答解不稳定。根据地球椭球模型，地面点三维坐标应该满足如下关系

(13)

式中，a和b分别代表椭球长、短半轴；h代表地面点高度。天场内定标要求的多时相影像成像角度相近，高程误差对同名点交会的影响可以忽略不计。因此，式(13)中h可以从SRTM-DEM数据中获取概略值，此时h为已知值，则式(13)可化为

(14)

假设从多时相影像中获取了N对同名点，则根据式(12)和式(14)可以构建法方程如下

V=At+BX-L

(15)

式中，t=[da0,…,daj,db0,…,dbk,dφu,dωu,dku]代表内定标模型参数改正数；X=[dX1,dY1,dX2,dY2,…,dXN,dYN]代表同名点地面坐标的改正数；A和B代表式(12)中对t和X的偏导；根据最小二乘原理实现对t和X的求解，完成无场内方位元素定标。

1.3 光学几何定标研究进展

国外在星载光学几何领域发展相对成熟，尤其是法国，自1986年发射SPOT 1以来，一直开展高精度几何定标研究，在全球范围内建立了21个几何定标场，对SPOT系列卫星实现了高精度几何定标。如2002年发射SPOT 5卫星后，法国空间中心(CNES)组织相关部门，建立了星敏相机光轴夹角误差模型及5次多项式拟合的内方位元素误差模型，采用分布定标策略，实现了精确校准[9-10]；最终SPOT 5单片无地面控制平面定位精度达到50 m(RMS)，无控制下的多立体像对高程定位精度达到15 m(RMS)[3,11]。SPOT系列的后续卫星SPOT 6和SPOT 7，其无控平面精度达到7.8 m，高程定位精度达到2.5 m，而内精度优于0.5像元[12]。

美国1999年发射的IKONOS卫星是世界上第1颗高分辨率商业卫星。卫星发射后美国国家宇航局等单位对其进行了在轨几何定标，以保障几何定位精度。利用Denver、Lunar lake等多个几何定标场，对各像素在相机坐标系下的指向(the field angle map,FAM)及相机星敏光轴夹角(interlock angles)进行了定标[4,13]，最终在无地面控制条件下达到平面12 m(RMS)、高程10 m(RMS)的定位精度[14]；类似于IKONOS，美国研究者采用航空影像对GeoEye-1卫星的FAM及Interlock angles进行了周期性定标，如2010年对Interlock angles进行了4次定标更新[15]，最终，GeoEye-1无控定位精度优于3 m[5,16]；文献[17]对2003年发射的Orbview-3卫星进行了在轨几何定标，建立了严格而灵活的自定标区域网平差模型，结合精密定轨、基于联合卡尔曼滤波的姿态确定(解求了星敏陀螺指向关系)等算法。最终，利用覆盖美国德克萨斯州几何定标场的13景全色影像及2景多光谱影像完成了定标解算，单片无控制点平面定位精度达到10 m (RMS)，立体像对平面定位精度达到7.1 m(RMS)、高程定位精度达到9.1 m(RMS)；而以美国DG公司分别在2014/2016年发射的Worldview-3/4卫星为代表，是目前全球分辨率最高的商业遥感卫星，其空间分辨率可达0.31 m，无控条件下的平面精度2.7 m，高程精度1.6 m。

日本2006年发射的ALOS卫星，其搭载的PRISM (panchromatic remote-sensing instrument for stereo mapping)传感器带有前视、正视、后视3个相机。ALOS标定小组开发了一套软件系统SAT-PP (satellite image precision processing)，该软件采用整体定标技术，利用附加参数的自定标区域网平差方法，解求了3个相机的总共30个附加参数；利用分布于日本、意大利、瑞士、南非等地的多个地面定标场进行在轨几何定标，最终无控平面定位精度达到8 m，高程定位精度达到10 m[18-19]。

2011年法国发射Pleiades卫星后，CNES的研究人员利用该卫星的高敏捷成像能力，提出了不依赖于几何定标场的系列自定标方法，在不依赖外部高精度控制数据的条件下实现了系统误差的消除补偿，并得到了不逊于常规定标场方法的定标精度[20]，该方法的实现，依赖卫星的高敏捷和高稳定性。

国内对线阵推扫式光学卫星的在轨几何定标研究起步较晚，且研究初期主要针对外方位元素定标。文献[21]分析了不同姿态角对几何定位的影响，提出了利用不同成像条件影像分别求解偏置矩阵角度的方法，最终遥感二号无控制定位精度达到152 m[21]；文献[22]研究了资源一号02B系统误差补偿方法，将其定位精度从860个像素提升至216个像素。姿态系统误差补偿，虽然对提升卫星影像的系统定位精度有一定效果，但却无法消除相机内部高阶畸变，导致定标后的影像定位模型中仍然存在较大几何畸变[22]。国内学者逐渐重视对内方位元素定标的研究，2012年我国首颗民用立体测绘卫星资源三号发射以后，文献[23—28]提出了多定标场联合的在轨几何定标模型，消除了资源三号各载荷安装误差、相机畸变等系统误差，最终资源三号无控制条件下平面精度优于10 m，高程精度优于5 m；带控制条件下平面精度优于3 m，高程精度优于2 m[23-28]。文献[29]以相机安装角及指向角作为外、内检校参数对资源一号02C全色相机进行在轨几何检校，最终检校后带控制定位精度在1个像素左右[29]；文献[30]利用Landsat8数字正射影像与GDEM2数字高程模型，对高分四号卫星进行在轨几何定标，几何定位精度明显提升，标定后精度优于1个像素。

国内针对交叉定标无场定标的研究较少。文献[31]提出基于全球Google Earth、SRTM等公众地理信息数据来完成资源一号02C卫星P/MS相机的几何定标，并取得了较好的结果；但是，该方法受限于公众地理信息数据的自身精度，并不能满足亚米级卫星的高精度几何定位；针对外方位元素定标，文献[32]提出了不依赖地面控制点的外方位元素自定标方，采用仿真数据验证了方法的正确性，结果表明该方法能够补偿外方位元素误差，有效提升无控几何定位精度；文献[33]提出基于星敏-相机恒星观测的安装定标方法，利用Loujia-1 02星开展了在轨试验，结果表明该方法在不依赖地面控制的条件下，可实现与基于场地定标方法相近的定位精度。针对内方位元素定标，文献[34]借鉴辐射交叉定标思想，提出一种多星小交会角影像的几何交叉定标方法，利用YG-4、ZY-3 01和ZY-1 02C卫星在轨数据开展了试验验证，表明几何交叉定标与定标场定标精度仅相差0.1像素左右；文献[35]提出了一种单星无场内方位元素定标方法，利用同一颗星对同一区域拍摄的小交会角影像，通过同名点定位一致性约束准确恢复内方位元素，利用ZY-1 02C卫星影像开展了试验验证，结果表明在完全不需要高精度控制的条件下，无场定标与场地定标精度仅相差0.02像素。

2 星载光学辐射定标基本原理与研究进展

2.1 光学辐射定标基本原理

光学遥感卫星辐射定标(以下简称“光学辐射定标”)是各类遥感观测产品得到有效应用的基础。辐射定标是建立遥感器每个探测器输出值与该探测器对应的实际地物辐射亮度之间的定量关系[36-37]。光学辐射定标可分为相对辐射定标和绝对辐射定标，相对辐射定标是去除传感器本身因传感器各成像探元响应差异引起的探元级误差，绝对辐射定标是将相对辐射定标后的图像信息转换为实际地物辐射亮度或地表反射率、表面温度等物理量有关的量[38]。

光学遥感卫星传感器辐射定标模型一般符合线性模型，如式(16)

DN(k,n,b,m)=A(k)×g(k,n,b)×γ(k,b)×v(k,b)×G(m,k)×L+

C(k,n,b,m)

(16)

式中，k为传感器波段序号；n为传感器探测器各探元序号；b为传感器探测器序号；m为传感器模拟增益；L为传感器入瞳辐射亮度；DN为传感器记录灰度值；A为传感器辐射亮度转换系数；g为传感器探测器各探元响应非均匀性系数；γ为传感器探测器各读出寄存器间响应差异系数；v为传感器各探测器间响应差异系数；G为传感器模拟增益系数；C为传感器暗电流响应值。可将式中辐射定标模型参数分为两类：一类是相对辐射定标参数，用于校正遥感卫星光学系统渐晕、传感器探测器各探元间、各读出寄存器间、传感器探测器各探元暗电流响应差异，包括传感器各探元间响应非均匀性参数g、传感器各读出寄存器间响应差异系数γ、传感器各探测器间响应差异系数v和传感器暗电流响应值参数C；一类是绝对辐射定标参数，用于将经相对辐射定标后的传感器记录DN值转换为传感器入瞳辐射亮度L，包括传感器辐射亮度转换系数A、传感器模拟增益系数G和积分时间或曝光时间转换参数。

根据辐射定标模型中各参数功能差异，可将式(16)转换为相对辐射定标公式(17)和绝对辐射定标公式(18)

DN(k,n,b,m)=g(k,n,b)×γ(k,b)×v(k,b)×

(17)

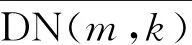
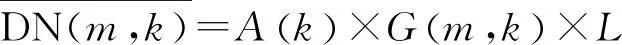
(18)

当传感器成像探测器因材料或制造工艺产生非线性模型时，传感器非线性响应模型即入瞳辐射亮度L与传感器记录DN值由传感器实验室定标数据予以高精度确定，如Pleiades HR传感器的双线性模型[39](式(19))

(19)

亦可采用高阶多项式模型(式(20))表达光学遥感卫星传感器非线性模型

DN=anLn+an-1Ln-1+…+a1L+a0

(20)

传感器辐射定标是通过提供高精度的辐射定标基准即传感器入瞳辐射亮度L标定上式中传感器探测器各波段各探元的定标参数，解决传感器记录DN到传感器入瞳辐射亮度L的转换。

光学辐射定标精度受制于传感器相对辐射定标模型精确性和辐射定标基准的准确性。辐射定标模型方面，国内外主流光学遥感卫星传感器相对辐射定标模型均采用线性模型，如ZY-3 01/02、SPOT 4/5、EO-1、Landsat 7/8、IKONOS 2、WorldView 2/3等卫星；但也存在因传感器各探元在量化范围内响应展现为分段线性，而采取分段线性定标模型的非线性模型，如Pleiades-HR传感器的双线性模型。辐射定标基准获取方面，不同的光学辐射定标方法，辐射定标的基准不同，如卫星发射前实验室定标的积分球[40]、星上定标方法的星上内定标灯或漫反射板[41-44]、基于场地定标的地表大面积均匀场或灰阶靶标等；此外，对相对辐射定标方法而言，还包括基于均匀场定标方法及偏航定标方法的地球表面大面积均匀场和在轨统计定标的海量影像样本下的相同灰度分布[45-46]等。

当卫星传感器辐射定标模型已知后，即可利用辐射定标基准解求模型参数，实现光学卫星传感器的辐射定标。

2.2 相对辐射定标研究进展

根据传感器相对定标参数类型的不同，在轨相对辐射定标方法可细分为暗电流定标和相对增益定标。暗电流定标是标定传感器在卫星传感器无光入射时，各探元的响应值及各探元间响应值的不一致性，即标定光学辐射定标模型中的暗电流响应值参数C；相对增益定标是标定传感器在不同入射光强下各探元的响应模型系数，即标定光学辐射定标模型中的传感器各探元间响应非均匀性参数g、传感器各读出寄存器间响应差异系数γ以及传感器各探测器间响应差异系数v。

2.2.1 暗电流定标

基于星上搭载定标设备的不同，星上暗电流定标可分为两类：①基于星上遮光挡板定标：在卫星处于地球背面时，用遮光挡板遮挡卫星入光口，传感器同时记录各探元暗电流响应值；常见于国外卫星传感器如SPOT 5-HRG、Landsat-8 OLI，QuickBird 2等[44,47-51]；②基于传感器无感光探元定标：利用传感器焦面特殊设计无感光探元，记录传感器电子学暗电流，如ADEOS-AVNIR、Landsat-8 OLI，RapidEye-MSI、WorldView系列等卫星[50,52-53]。星上暗电流定标方法可实现超高频次的暗电流定标和高定标精度，如Landsat 8 OLI传感器每轨成像前后各进行一次基于星上遮光挡板的暗电流定标[50]，暗电流定标后传感器可见光近红外波段暗电流噪声优于0.09(1δ)[44]；SPOT 5-HRG传感器基于星上遮光挡板实现了分钟级的星上暗电流定标[47]。

对于无星上定标设备的卫星传感器而言，采用间接遮挡卫星传感器入瞳光照的形式实现传感器暗电流定标，包括卫星夜间对深空背景成像，常见于QuickBird 2，Pleiades等卫星[51,74]，以及夜间对均匀海洋区域成像，如ADEOS-AVNIR、ALOS-PRISM、NOAA-AVHRR、QuickBird 2、RapidEye MSI、SPOT 5-HRS等卫星[47,51-53]。受限于卫星任务规划和观测条件，夜晚成像的暗电流定标方法在定标频次相比较星上定标大幅降低，定标精度低于星上定标，如ADEOS-AVNIR传感器[52]一个月内进行两次在轨对夜间海洋成像的暗电流定标，暗电流测量精度上优于0.2个DN。

2.2.2 相对增益定标

目前国内外常用的相对增益定标方法有：星上定标、在轨均匀场定标、统计定标以及偏航辐射定标等方法。

星上定标方法依赖于星上搭载的各类定标设备，如ALOS卫星、IKONOS卫星、SPOT系列卫星、EO-1卫星、Landsat系列卫星和CBERS-01卫星搭载的星上定标灯设备[38,44,47,50,52,54-59]以及AQUA/Terra卫星、QuickBird卫星、EO-1卫星、Landsat系列卫星和高分五号卫星搭载的星上漫反射板设备[60-63]。星上定标方法不受地球大气的影响，可实现高精度的在轨定标，如Landsat 8卫星基于星上漫反射板定标后传感器VNIR/PAN波段平均条纹系数优于0.005%[38]。但该方法受限于星上定标设备，一般只能利用两个亮度等级样本点标定传感器线性模型，无法实现传感器非线性定标，且星上定标灯或太阳漫反射板存在时间衰减性，会引起传感器焦面非均匀性光照，降低了星上辐射定标精度。

在轨场地定标是利用地球表面大面积均匀场地物进行传感器在轨相对辐射定标的一种方法。常用大面积均匀场主要有沙漠、森林、海洋、南北极雪、深对流云(deep convective clouds,DCCs)等，国外主流线阵推扫式光学卫星均利用过此法进行在轨定标，如ALOS、IKONOS、Landsat、QuickBird 2、WorldView、SPOT、RapidEye等卫星[38,47,51,53,64-69]。SPOT 5卫星采用南极均匀雪场景完成了HRG和HRS传感器的在轨相对定标，定标后传感器各探元列均值标准差的RMS优于0.02个DN[47]；Landsat 8 Circus波段采用DCCs方法实现了最大条纹系数优于0.4%的定标精度[38]。

在轨统计定标方法通过在轨传感器成像数据样本量的积累，基于统计规律标定探元间响应，根据统计策略的不同具体可分为基于均值标准差统计法(Landsat-4 MSS)、直方图匹配法(Landsat-7 ETM+)和基于阈值分割均值方差统计法(生命周期统计法)(EO-1、Landsat-8)等[45,57,70-72]。均值标准差统计法受传感器成像地物亮度分布影响较大，定标校正效果不稳定，如传感器成像地物亮度绝大部分位于传感器的中亮度区间内，低亮度区间几乎无数据，而少许高亮地物如云、雪、冰等往往造成传感器成像饱和，会引起统计定标系数畸变；当传感器各个响应存在非线性响应且非线性响应不一致时，线性定标会造成不同亮度范围校正不一致，造成低高亮度区间校正效果差。直方图匹配方法因传感器在轨图像灰度分布不均，高亮度饱和、低亮度过低，导致高低亮度区间难以解算出有效参数，且需要海量样本的积累，实际在轨定标工作量较大。从EO-1发展而来的阈值分割统计法，则依据均值方差阈值将图像分类，利用分类后图像数据基于传感器各探元均值或方差解算传感器相对增益系数，该方法需要统计大量数据，且查询统计结果需要耗费大量时间，对传感器非线性响应无法取得理想效果。统计定标方法的定标精度受定标样本影响较大，在传感器不同亮度范围内存在较大波动，如EO-1生命周期统计定标法[72]，在低亮度影像上定标精度(@条带系数)优于0.8%，在中亮度影像定标精度优于0.3%，在高亮度影像定标精度优于0.2%。

随着遥感卫星敏捷机动成像能力的发展，遥感卫星能够在敏捷机动条件下成像为线阵推扫式传感器在轨相对辐射定标带来新契机。文献[73]在2004年首次提出利用卫星敏捷能力进行在轨相对辐射定标的“side-slither”概念，将卫星旋转90°成像，使得线阵传感器各探元依次经过地面相同地物，以此标定为线阵传感器各探元响应模型。因需卫星偏航90°后对地成像，“side-slither”方法也称为偏航辐射定标方法。该方法自提出以来已在国内外多颗卫星得到具体应用，如QuickBird 2、RapidEye、Pleiades、Landsat 8、YG-25、GF-9等卫星，并取得较高的定标精度[38-39,53,73-80]，如QuickBird传感器定标后全色和多光谱波段定标精度(@条纹系数)优于0.6%[51,73]；Pleiades-HR传感器全色波段定标精度(@NeDLI指标)优于2[74]；Landsat-8 OLI传感器和GF-9传感器各波段定标精度(@条纹系数)分别优于0.1%和1%[38,80]。

为了保证幅宽，光学卫星传感器CCD拼接模式采用“品”字型拼接，如QuickBird-2、Landsat-8 OLI、RapidEye等卫星[51,81-82]。此类卫星在偏航辐射定标方法的实际在轨应用中，为了使得传感器所有CCD在卫星偏航定标成像的过程中能够依次经过地表相同地物，其偏航辐射定标成像需要依赖对地表均匀场地物。对卫星传感器具备较好的探元线性度时，基于均匀场的偏航定标方法可取得较为理想的定标效果，但对于一些因传感器探元在不同亮度范围内的响应模型存在差异且不同探元的响应模型也存在差异的卫星传感器而言，该方法并不能取得良好定标效果，且无法实现传感器全动态范围的在轨相对辐射定标[83]。基于此，文献[79]提出基于卫星敏捷能力的无场在轨相对辐射定标方法，可实现线阵推扫式光学卫星传感器高精度、全动态范围、高频次在轨相对辐射定标。

2.3 绝对辐射定标方法

绝对辐射定标是建立地物真实辐射亮度与相对辐射定标基准之间的关系，解求光学辐射定标模型中的传感器辐射亮度转换系数A以及传感器模拟增益系数G。光学绝对辐射定标方法除卫星发射前实验室定标、星上定标方法之外，常用方法包括场地定标方法(替代定标方法)、交叉定标以及月球定标方法等。

场地定标方法基于地面辐射定标场的星地同步观测实现光学传感器绝对辐射定标。在卫星过境时，通过地面或飞机上准同步测量，基于大气辐射传输模型解算遥感卫星入瞳辐射亮度，按照式(18)计算传感器绝对定标参数。根据地面同步测量内容的差异又分为反射率基法、辐亮度基法和辐照度基法3种[84]，可取得3%～5%[85]的绝对辐射定标不确定度。为此，全球范围内建设了诸多辐射校正场，比如美国白沙辐射定标场、法国LaCrau辐射定标场以及中国敦煌辐射定标场等。但场地定标方法需要星地同步观测，耗费大量的物力、人力，且测量易受到大气条件的限制，能获取的定标数据有限，定标效率较低。

交叉辐射定标以高辐射定标精度的传感器为基准，与待定标传感器同步拍摄同一区域，并以地面大气和光谱测量数据或历史大气光谱数据为辅助，对待定标传感器进行绝对辐射定标的一种方法，也是卫星传感器稳定性监测的定标和校验方法，可取得1%～2%的交叉辐射定标精度[86]。目前，交叉辐射定标用于在轨绝对辐射定标已成功应用与国内外多颗遥感光学卫星，如MODIS与ATSR-2、Landsat TM与ETM+的绝对辐射定标[87-88]。卫星传感器稳定性监测应用方面，通常采用基于伪不变地物目标交叉辐射定标方法监测卫星传感器稳定性状态，如用伪不变目标时间序列图像监视Landsat-5 TM、Landsat-7 ETM+以及FY-3A MERSI等卫星传感器在轨响应状态的衰减[89-91]。

近年，文献[92]通过长时间对月球光谱特征和反射特性分析，发现月球是个非常稳定的辐射光源，且光谱宽而平滑。文献[93—94]提出利用对月源长期观测实现遥感卫星传感器的在轨辐射定标和稳定性监测，将月球作为辐射源引入光学传感器辐射定标，即月球定标。精确的月球辐射模型是为了实现遥感卫星传感器基于月球观测辐射定标的基础。目前，基于地基对月辐射测量，不少研究者建立了月球辐射模型，如MT2009模型和ROLO模型。MT2009模型基于地基周期性对月观测获得的月球光谱反射率数据集合建立[95]，但MT2009模型数据源多，没有溯源到同一标准，且未顾及月相角的正负和月球天平动对月球辐射照度的影响，不确定性较大，应用受到较大限制[96]。ROLO模型是基于通道式月球成像仪器对月球进行周期性辐射观测而建立的月球辐射模型，ROLO观测期间获得了350～2500 nm波段内32个通道83 000次月球观测数据，数据量大、数据源一致，且模型的建立充分考虑了反冲效应、天平动、月球相位角、观测距离等因素的影响，适用性好，应用广泛。目前USGS基于ROLO模型已建立了利用月球光谱辐照度的遥感卫星传感器月球定标方法，已成功地应用Suomi NPP、SeaWIFS等遥感卫星传感器的在轨定标和稳定性监测[97-98]。研究表明[96,99-100]，ROLO模型在可见光近红外波段精度较高，绝对不确定度为5%～10%，相对不确定度为1%～3%。

3 星载SAR几何定标原理与研究进展

3.1 场地几何定标

针对星载SAR几何定位，其主要误差可分为4类[101]：第1类误差主要包括本地振荡器漂移引起的误差、晶振标称值误差和晶振稳定度引起的误差、传感器电子时延引起的误差和方位向时间误差；第2类误差主要包括轨道误差，可通过星上配置双频GNSS，并进行事后精密定轨来提升；第3类误差主要为大气传播延迟误差，为时变误差，可利用大气延迟改正模型来改正；第4类误差主要为没有抵制干净的传感器电子时延和方位向时间误差，需通过在轨几何定标来修正。

从SAR系统的工作原理出发(图4)，可在SAR系统的天线处将雷达信号的延迟影响分为两种，即传感器电子时延影响和大气传播延迟影响。传感器电子时延是距离向系统误差，是星载SAR几何定标参数；SAR信号的发射和接收都是在时间尺度上完成的，主要为方位向时间误差，该时间误差主要影响方位向的定位精度，是星载SAR几何定标参数。

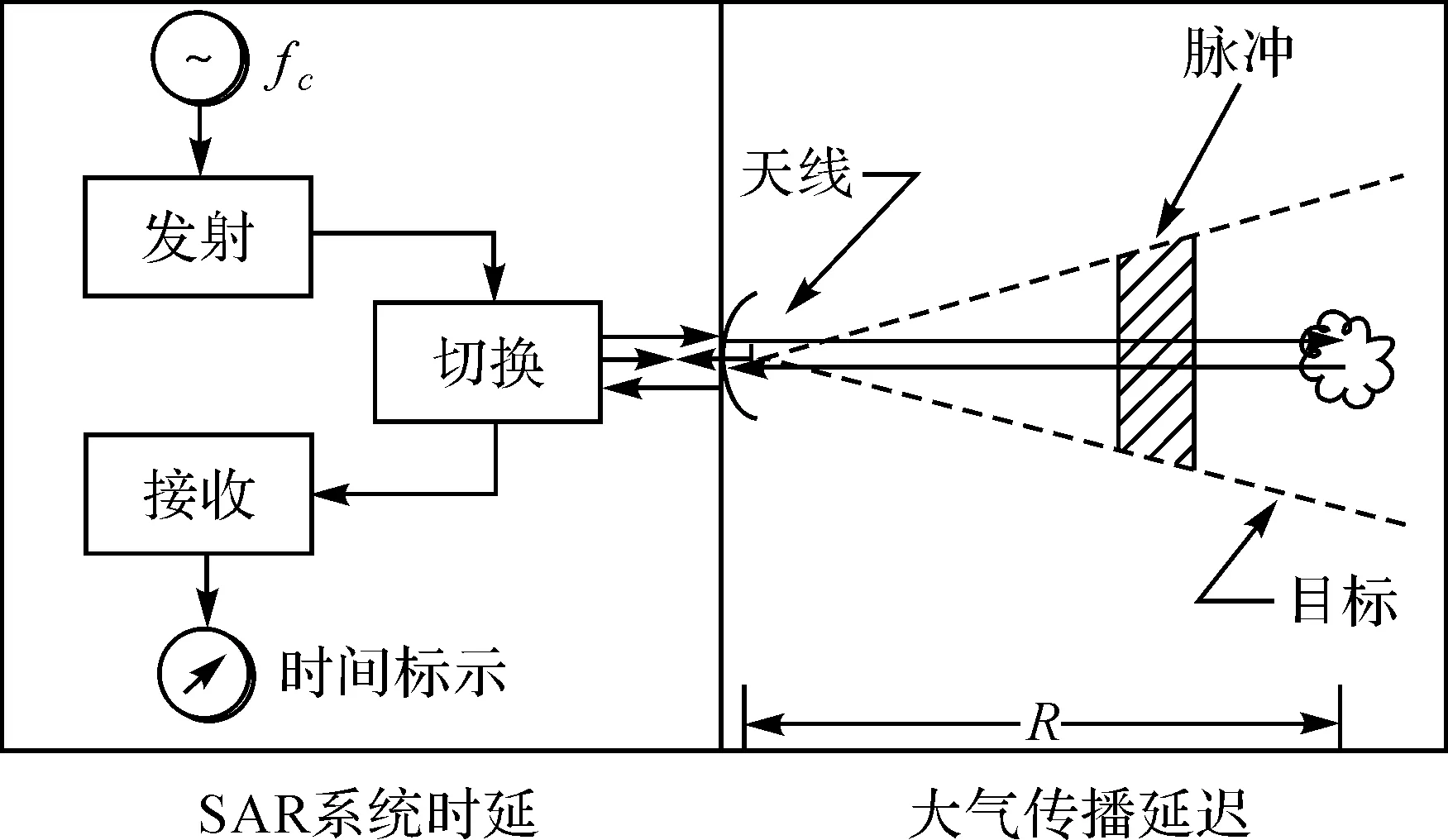
图4 SAR系统工作原理Fig.4 Principle of SAR system

大气传播延迟是时变误差，主要受大气环境影响，可以根据目标点所处的中性大气和电离层环境参数通过大气传播延迟改正模型进行消除。

雷达信号受大气层延迟的影响，而这种影响随着传播路径的增加而变大，并且雷达信号随大气环境的变化而变化。当SAR卫星以不同入射角进行成像，或者以不同升降轨形式进行，或者以不同时间对不同地点进行成像，雷达信号传播路径的改变影响着斜距测量精度，导致几何定标精度受到影响。因此，大气传播延迟影响星载SAR几何定标精度。

构建星载SAR几何定标模型

(21)

式中,tf、ts分别为距离向时间和方位向时间；tf0、ts0分别为距离向起始时间的测量值和方位向起始时间测量值；tdelay为大气传播延迟；Δtf、Δts为传感器电子时延误差和方位向时间误差；x、y为像素坐标；width、height分别为SAR影像的宽和高。

Δtf主要为雷达信号经过信号通道的各个器件时产生的系统时延。该系统时延可以通过地面实验室标定的形式获得，但由于卫星发射时雷达载荷器件会发生变化，进而影响雷达信号的系统时延。Δts实际是SAR载荷和GNSS载荷之间时间同步误差。

通过间接定位算法可以建立起地面点坐标与方位向时间和星地距离的对应数学关系，而方位向时间和星地距离又是与SAR影像方位向行号和距离向列号一一对应的，通过最小二乘平差就可以精确计算方位向开始时间、距离向起点时间，可以计算几何定标参数。

3.2 交叉几何定标

图5所示为Sat1、Sat2卫星分别对同一地物点T成像，且分别成像于SAR影像的像元t1和t2处。假定Sat1、Sat2卫星的成像几何参数(包括测量的轨道、斜距和多普勒参数)准确无误，且地物点S高程已知，则根据几何定位模型进行计算，t1和t2都应该定位于T所处的地面坐标；然而，利用卫星下传的真实数据，通常难以使t1和t2定位于地面同一点(图中ΔS所示偏差)，这是因为：①几何模型参数误差的影响；②地面点T高程未知，成像角度差异产生投影差。

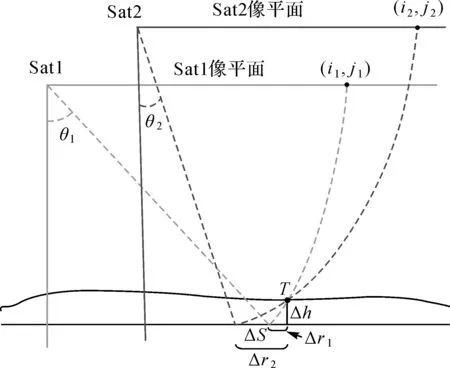
图5 同名点两次成像Fig.5 Two imaging process of the identical point

图5中，仅考虑高程误差对同名点交会的影响，则

ΔS=(Δh/tanθ2)-(Δh/tanθ1)

(22)

式中，θ1和θ2分别为前后两次成像的入射角；Δh为高程误差。显然，Δh取决于几何定位时采用的地形数据(如全球公开的SRTM-DEM数据)，因此，当θ1和θ2足够接近，即卫星以非常相近的入射角连续两次拍摄同一区域时，则可消除高程误差对同名点交会的影响。在此条件下，同名点交会仅受到几何模型参数误差的影响，可表示如下

ΔSi=fSat1(t1i)-fSat2(t2i)

(23)

式中，fSat1、fSat2分别为Sat1、Sat2两影像同名像元处的成像几何模型参数误差。现假定Sat1影像经过几何定标参数校正，即fSat1=0，则式(23)可写成

ΔSi=-fSat2(t2i)

(24)

由式(24)，可以通过同名点交会误差来标定Sat2影像的几何定位参数误差。

3.3 无场几何定标

图6所示为星载SAR无场几何定标原理示意图。图6(a)中有同一颗SAR卫星的两张SLC影像，S1和S2是两张SLC影像对应SAR卫星天线相位中心，不规则曲线为真实的地表，点A为地表上的地物点。当不存在任何误差时，S1与物方点A之间的斜距为R1，S2与物方点A之间的斜距为R2，则A实际上是斜距R1和斜距R2在物方上的前方交会点。实际上，由于存在影像系统误差(如斜距误差ΔR)，它们的前方交会点为B。总之，斜距存在系统误差，进而导致交会的物方点坐标的变化。

然而，由于实际的物方点A的坐标是未知的，所以图6(a)也可以反过来解释成物方点A的坐标误差导致了影像斜距变化。因此，两张影像无法区分到底是影像系统误差还是物方点坐标误差导致斜距误差的存在。

为了解决这个问题，如图6(b)所示引入了第3张影像S3。物方点A与影像S3天线相位中心之间的斜距为R3，当不存在任何误差的时候，3张影像的交会点为A，实际上，由于误差的存在，S3和S1的前方交会点为C，和S2的前方交会点为D。如果斜距测量的误差是由物方点坐标误差引起的，则前方交会点B、C和D应该是同一个点，即坐标值应该一样；如果斜距测量的误差是由影像系统误差引起的，则前方交会点B、C和D有可能不一致，这种不一致称为交会残差。

通过以上分析，3张SLC影像之间同名点的交会残差可以作为几何定标参数求解的一个准则，几何定标参数可以通过约束交会残差最小来探测得到。

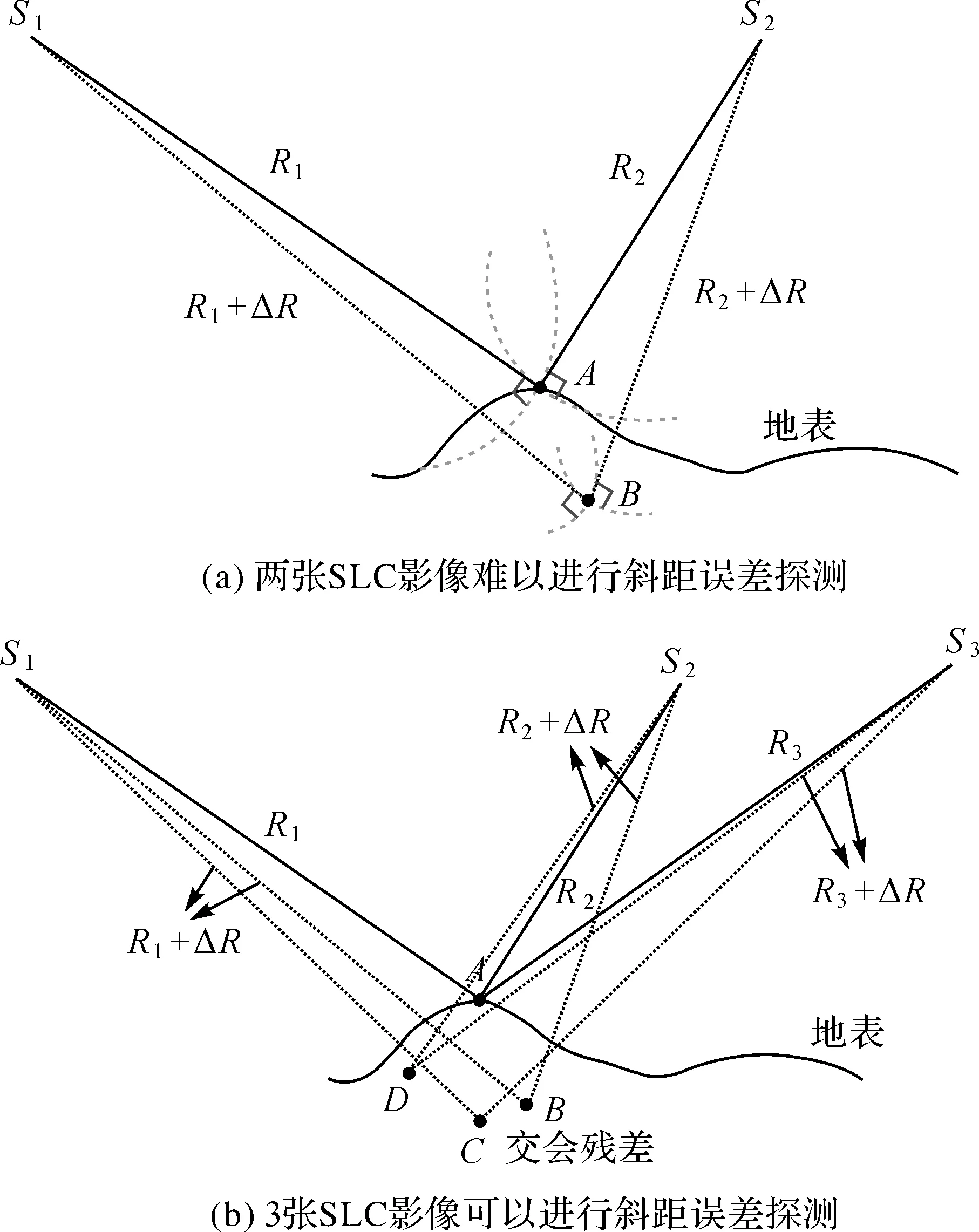
图6 星载SAR无场几何定标原理Fig.6 Calibration-field-free geometric calibration principle of spaceborne SAR

3.4 SAR几何定标研究进展

在星载SAR领域，几何定标和几何校正是容易混淆的两个概念，几何校正是对遥感数据本身真实性的还原[102]，遥感成像时，由于平台的状态参数、地球自转以及地形起伏等因素的影响，造成影像相对于地面目标发生几何畸变，几何校正就是消除这种畸变，给数据本身加上真实对应的几何坐标信息，是对数据本身真实性的还原。SAR影像几何校正的精度取决于SAR系统提供的各种定位参数的精度，几何定标就是对各种定位参数误差进行标定，是对定位参数真实性的还原[103-104]。但早期几何校正和几何定标并没有做区分，几何定标和几何校正都是指赋予影像平面坐标和高程信息，如日本的JERS-1[105]，其几何定标本质上是多项式几何校正，依据地面控制点(ground control point，GCP)构建地理坐标空间，然后在图像空间与地理坐标空间之间建立多项式变换关系模型，实现图像坐标向地理坐标的变换。多项式几何纠正需要地面控制点，在地形起伏区域几何纠正精度低，逐渐被基于距离-多普勒模型(range Doppler model，RD模型)的纠正方法所替代。RD模型是利用目标回波中包含的距离信息和多普勒历程信息来构建距离方程和多普勒方程，最早由Brown在1981年提出，后来由Curlander发展并应用到星载SAR几何定位中[106-107]，基于RD模型，在无须GCP的情况下即可解算每个像元的地理位置坐标，但构建RD模型所需的定位参数，其准确性直接影响影像的无控制点定位精度。美国的SIR-C/X系统就是利用RD模型来进行SAR图像的几何定标，由于早期的卫星轨道精度较低，所以SIR-C/X系统的定标原理与加拿大的Radarsat-1一样，都是通过布设地面控制点来解算轨道参数的系统误差，从而提高影像的几何定位精度[108]。由此开始，几何定标与几何校正逐渐区分开来。

ERS-1是世界上首颗实现高精度几何定标的卫星，利用地面检校场对ERS卫星影像进行几何定标处理，标定影响影像无控制几何定位精度的关键系统参数，最终单片无控制点平面定位精度达到10 m(RMS)[109]。此后的星载SAR几何定标均是针对系统参数进行，本质是构建几何定标模型，通过控制点在影像平面上的真实位置与计算位置的差值来解算出定标参数，利用定标参数对几何定位模型参数进行误差补偿，从而提高影像的无控制点几何定位精度。几何定标参数与卫星制造水平高度相关，早期SAR卫星定轨精度差，几何定标主要是对轨道位置进行修正，随着定轨精度的提高，卫星位置偏差对最终几何定位精度的影响较小，而距离向的系统时延和方位向时间误差成为影响影像无控制点定位精度的最主要因素，Envisat-1、ALOS、Radarsat-2、TerraSAR-X、TanDem-X和Sentinal-1A/1B的几何定标参数主要是距离向的系统时延和方位向时间误差[110-113]。随着控制点精度的提高，大气延迟影响成为制约星载SAR几何定标精度的关键因素，需要在定标过程中加以考虑[114]。

我国SAR卫星起步比较晚。前期对星载SAR的几何定标研究主要利用国外星载SAR数据开展，如文献[115]利用遥感1号数据，选择距离向初始时间延迟测量误差、距离向采样率误差、方向初始时间误差、方位向脉冲重复频率误差作为定标参数，通过定标处理，现在提高了影像定位精度。随着国产SAR卫星的陆续发展，开始了国产SAR卫星几何定标相关研究。文献[116—117]利用地面高精度控制点数据和外部大气参考数据，采用基于大气传播延迟改正的多模式星载SAR混合定标方法，对遥感13号和高分三号SAR卫星进行几何定标处理，经验证，定标后的几何定位精度均优于3 m。文献[118]提出一种基于稀少控制的多平台星载SAR联合几何定标方法，采用TSX/TDX影像和GF-3影像验证了该方法的有效性和正确性。由以上文献可知，SAR卫星的几何定标工作主要依赖于地面高精度控制数据，一定程度影响SAR卫星几何定标工作效率。针对SAR卫星的重放周期低、高精度控制数据获取成本高等问题，国内学者开展了不依赖地面控制数据的几何定标方法研究。文献[119]基于相同入射角条件下高程引起的同名点定位误差可以抵消的原理，提出了星载SAR交叉几何定标方法，利用遥感13号和高分三号SAR卫星影像数据验证了方法的有效性。文献[120]基于同名点交会残差最小约束的原理，提出了星载SAR无场几何定标方法，与场地几何定标方法相比，定标后的几何定位精度仅差2.53 m。

4 星载SAR辐射定标原理与研究进展

4.1 SAR辐射定标基本原理

星载SAR辐射定标的目标为：测定天线方向图和测定雷达系统总体传递函数(或定标系数)。

4.1.1 方向图测量

星载SAR天线方向图的不确定性是SAR辐射定标的主要误差源之一，天线方向图在轨测试是星载SAR定标技术的关键部分。星载SAR在轨天线方向图测量方法可以用标准点目标(角反射器或有源定标器)测量法、均匀分布目标测量法。

4.1.1.1 标准点目标(角反射器或有源定标器)测量法

标准点目标(角反射器或有源定标器)测量距离向双程方向图方法是将一系列经过精确标定的标准点目标(角反射器或有源定标器)沿着垂直于卫星飞行的方向均匀放置于测绘带内，并且精确标定标准点目标(角反射器或有源定标器)的地理位置及海拔高度，调整好各标准点目标(角反射器或有源定标器)的指向角。由于经过成像处理后，图像中的点目标响应能量的大小反映了回波信号在距离向上受距离方向图调制程度的大小，结合点目标在距离方向图中的角度位置，可解得距离双程天线方向图采样值为

(25)

式中，Pi是发射信号功率；Ri是合成孔径雷达与目标的斜距；K为常数；σi为第i个目标的雷达截面积。

4.1.1.2 分布目标法测量法

分布目标法测量距离双程方向图是对具有均匀后向散射系数的分布目标，如亚马孙热带雨林，进行成像处理后，图像距离向灰度值的大小反映了回波信号在距离向上受方向图调制程度的大小，结合图像不同区域在距离方向图中的角度位置，即可测得距离双程天线方向图

(26)

式中，Pd是接收信号功率；R是合成孔径雷达与目标的斜距；θ为入射角；K为常数；σ0为目标的后向散射系数。

4.1.2 绝对辐射定标常数计算

雷达系统总体传递函数的测定需要依靠地面已知雷达截面积的目标，其发展之路与点目标及相关算法息息相关。SAR绝对辐射定标时，目标的图像响应能量εp与其雷达截面积σ之间的关系由系统的总传递函数K确定，K即绝对辐射定标常数。三者之间的关系如下式

εp=Kσsin (θ)

(27)

绝对辐射定标常数一般通过在地面布设若干标准参考点目标进行计算，标准参考点目标的脉冲响应能量εp可以通过积分法或者峰值法进行提取。在地面布设N个定标器，εpi为第i个点目标的能量，σref是定标器的雷达截面积，θi第i个点目标的本地入射角，则第i个目标计算的定标常数为

(28)

4.2 星载SAR辐射定标研究进展

4.2.1 方向图测量

早期发射的星载SAR如美国的SIR-B、欧空局的ERS-2卫星等，其天线方向图主要采用标准角反射器方法进行测量，但该方法只能测试距离向天线方向图，测试精度受到多种因素的制约，同时测试成本较高、工作量大，因此在ERS-2之后标准角反射器测量方法便成了一种补充的测量手段[121]。与此同时，基于分布目标的距离向天线方向图测量方法成为主流，该方法利用亚马孙等自然分布目标即可完成距离向双程天线方向图的测量，大大节约了测量成本，测量精度能够达到0.3 dB，SIR-C，Radarsat由于标准角反射器方法和基于分布目标的测量方法都只能测量距离向双程天线图，为了实现对方位向天线方向图的在轨测量，人们开始研究利用地面接收机、地面发射机、有源定标器等有源测量设备来测量天线方向图[122-128]，地面接收机能够接收雷达脉冲信号并进行存储，因此沿距离向布设多个接收机可以完成距离向和方位向二维发射天线方向图的测量。而地面发射机可以向雷达卫星发射信号，雷达接收机接收信号，从而生成接收天线方向图，同样沿距离向布设多个发射机可以完成距离向和方位向二维接收天线方向图的测量。有源定标器兼具角反射器、地面接收机、地面发射机的功能。能够对SAR信号进行接收、放大和转发，因此，在现有主流星载SAR卫星天线方向图测量过程中，有源定标器的应用最为广泛[129-130]。

以上的测量方法均是采用具体目标对天线方向图进行测量，随着SAR新体制的发展，SAR工作模式不断增多，从而导致SAR实际工作时波位数量急剧增多，例如TerraSAR-X实际工作时，有超过12 000种不同波束需要进行标定，这使得在轨测试工作量非常大。为此，提出了基于有源相控阵天线数学模型的测量方法，该方法可以基于内定标数据和天线方向图模型快速计算出各波位天线方向图，满足了TerraSAR-X天线方向图在轨测试的需要[131-132]。

国内对星载SAR天线方向图在轨测试技术的研究相对较少。文献[133]研究了天线方向图地面接收机测量技术并分析了卫星轨道、姿态等误差因素对天线方向图测量精度的影响。文献[134]研究了利用地面发射机测量方法同时测量雷达接收天线二维方向图的测试技术，通过仿真模拟系统，进一步研究了各误差源对天线方向图测量精度的影响[134]。文献[135]研究了利用亚马孙热带雨林测量星载SAR俯仰向双程天线方向图，并用仿真数据进行了验证。近年来，国内对星载SAR天线方向图测量的研究鲜有报道[104]。

4.2.2 绝对辐射定标常数

绝对辐射定标就是求解星载SAR系统总体传递函数，也就是常说的绝对辐射定标系数。人工定标器，比如有源定标器、角反射器常用来测量绝对辐射定标常数，因为他们的雷达截面积已知，且精度较高(优于0.2 dB)，在定标时，一般选取后向散射系数较低的区域布设定标器，这样能使得定标器的RCS远大于背景区域的总散射功率，降低背景杂波的影响，提高定标精度[136-138]。

然而定标器的布设往往费时费力，因此，利用定标器进行SAR卫星绝对辐射定标常数的测量往往间隔周期较长，影响SAR影像的绝对辐射精度。人们通过研究发现，亚马孙热带雨林的雷达后向散射系数非常稳定，标准差小于0.3 dB，因此，人们发展了利用亚马孙热带雨林进行绝对辐射定标常数测量的方法，并取得了较好的效果[139-141]。

除了利用人工定标器、亚马孙热带雨林进行绝对辐射定标系数测量，国内外研究者还探索了基于沙漠、海洋、PS点等场景的绝对辐射定标测量方法，但这些方法都有其优缺点，走向工程实用还需进一步的研究[142-146]。

文献[147]提出了一种基于辐射稳定特性挖掘的SAR绝对辐射定标常数测量方法，并用Sentinel-1作为试验数据，提取了辐射稳定的城市切片，建筑切片散射稳定性优于0.19 dB，为SAR绝对辐射定标常数测量提供了一种方法。

5 前沿问题

在轨卫星受发射震动、空间环境变化、电子元器件老化、部件运动等诸多因素影响，卫星成像质量一般都会发生变化。但多数遥感应用都希望针对一颗卫星任何时候获取的产品的几何质量和辐射质量均保持在较高水准上，也就是获取可靠稳定的遥感数据，这就要求成像卫星在轨运行的全生命周期之内产出的产品质量保持不变。文献[101]定义了卫星成像质量可靠性的概念和内涵，提出卫星成像质量可靠性的研究方法包括可靠性设计、测试、增长和保持4个方面。

星载光学/SAR几何辐射定标研究后续建议从几个方面开展工作：①新体制光学SAR卫星几何辐射定标方法研究；②定标措施和方法要从在轨地面定标发展到在轨星上几何辐射定标；③定标时态要从瞬态的几何辐射定标发展为全生命周期的成像质量可靠性。