基于最小二乘策略迭代的无人机航迹规划方法

陈晓倩，刘瑞祥

北京联合大学 智慧城市学院，北京100101

1 引言

与有人机相比，无人机具有体积小、成本低、生存能力强、机动性能好、使用方便等优点，业已在空中作战、局势侦察、精细农业、电力巡检等领域得到广泛应用。航迹规划是无人机任务执行能力实现的核心技术之一，是指在综合考虑飞行时间、燃料消耗、外界威胁等因素的前提下，为无人机规划出一条符合任务需求和动态约束的最优航迹[1]。良好的航迹规划能力是无人机飞行任务优化执行的重要保证。

已有的无人机航迹规划算法包括A*算法[2]、遗传算法[3]、蚁群算法[4]、粒子群算法[5]及人工势场法[6]等。由于航迹规划的规划区域复杂多变，加之要考虑无人机的性能约束等条件，算法存在寻优能力差、计算量过大、效率不高等问题，在航迹规划的最优性和实时性方面有待进一步提高。

近年来，强化学习算法在无人机领域的应用日益得到关注。李东华等人采用多智能体强化学习的方法，采用两个功能不同的智能体，分别对应局部和全局路径规划[7]。郝钏钏等人利用无人机的航迹约束条件指导规划空间离散化并在回报函数中引入回报成型技术[8]。上述文献利用无人机的航迹约束条件指导规划空间离散化，一定程度上降低了离散规划问题的规模，提高了规划获得的航迹的可用性，但是航迹的精度直接与空间离散栅格尺度相关，在复杂应用场景中航迹精度无法保证。杨祖强等人采用Wire Fitting Neural Network Q（WFNNQ）学习方法实现了连续状态连续动作的航迹规划[9]。但连续的状态和动作采用神经网络逼近，训练时间较长，收敛性较差，不适合在线应用。

为弥补已有方法的不足，本文采用最小二乘策略迭代算法开展无人机航迹规划问题研究。该算法采用带参线性函数逼近器近似表示值函数，避免进行空间离散化，提高了航迹精度。同时最小二乘方法利用采集的样本数据求解值函数参数，直接对策略进行评价和改进。通过复杂城市场景中的飞行动力学仿真对算法的有效性进行了验证，并与经典的Q 学习算法进行对比，仿真结果表明LSPI 算法规划出的三维航迹更为平滑，规划时间更短，有利于飞机实际飞行。

2 问题描述

本文针对城市反恐、智能物流、抗震救灾等应用关注的无人机在复杂环境中的航迹规划问题开展研究。所提出的算法能够导引无人机安全无碰地从任一起始位置出发，到达目标位置，实现航迹长度、飞行高度、飞行安全性等指标的优化。

无人机航迹规划功能结构如图1 所示。任务规划器提供航迹规划的起始位置(X,Y,Z) 、目标位置(XT,YT,ZT)与速度(Vx,Vy,Vz)、航迹约束；基于算法的航迹规划器利用以上任务信息及无人机提供的当前位置速度信息生成新的动作(Vx,Vy,Vz) 并提供给无人机；无人机飞控系统对飞行动作进行解析得到无人机控制指令作用于无人机；无人机将下一位置(X',Y',Z')反馈给航迹规划和飞行控制模块。

基于上述任务场景和功能结构，本文所述航迹规划问题如式（1）所示。航迹优化的目标是使航迹费用J 最小，即找到一组具有最短航迹长度的可飞航迹。约束条件主要包括：航迹无碰和最大速度vmax。Co表示无人机与障碍物间的碰撞次数。

3 强化学习算法

3.1 MDP模型

强化学习是一种从环境状态到行为映射的学习技术。学习过程如下：Agent 通过对感知到的环境状态采取各种试探动作，获得环境状态的适合度评价值（通常是一个奖励或惩罚信号），从而修改自身的动作策略以获得较大的奖励或较小的惩罚[10]。马尔科夫决策过程（Markov Decision Process，MDP）常用来对强化学习问题进行建模[11]。MDP 问题通常可以用一个五元组{S,A,P,R,γ}来描述[11]，其中S 是状态空间，A 是动作空间，P 是状态转移概率，R 是立即回报（奖赏）函数，γ∈(0,1)是折扣因子。Agent 根据策略π 来选择动作。强化学习的目标是对于一个MDP 模型，获得最优策略π*满足式（2）：

其中rt为单步回报，Jπ为策略π 的期望折扣总回报。

3.2 最小二乘策略迭代算法

最小二乘策略迭代（Least-Squares Policy Iteration，LSPI）是一种基于逼近方法的强化学习算法，在值函数空间进行逼近[12]。经典的Q 学习算法对状态空间进行离散，采用查询表的形式存储动作值函数和策略，智能体能够到达的状态是有限的，不能遍历所有状态，离散尺度过大会降低系统精度。对于大规模或者连续空间问题，近似是一种有效的方法，可以遍历状态空间中所有的状态，保证系统精度。

关于策略π 的状态-动作值函数Qπ(s,a)定义为在状态s 下采取动作a，且后续动作都按照策略进行选择时获得的期望总回报[13]。Q 值根据式（3）的贝尔曼公式计算[14]：

其中R(s,a)表示在状态s 下执行动作a 后获得的立即回报；P(s,a,s')∈[0,1]表示在状态s 下选择动作a 后使环境状态转移到状态s' 的概率；π(a';s')表示策略在状态s'选择a'的概率。

图1 无人机航迹规划功能结构图

在大规模或连续空间中，对Qπ(s,a)进行逼近。通常使用线性函数逼近器将值函数表示为一组基函数φ1,φ2,…,φn的线性组合[13]，如式（4）所示，其中ω 是一个n 维的参数向量。

LSPI是一类无模型、离策略的近似迭代算法，离线方法有更好的样本利用率[15]。利用采样方法，根据样本数据来学习参数ω[16]。假设在任意策略π 下收集到N个样本：

其中：

LSPI 的结构框图如图2 所示[17]。策略评估中采用线性函数逼近器逼近Q 值函数，逼近形式如式（2）所示，策略改进中通过式（7）所示的贪心策略逐步改善策略，直到前后两次策略π[t]和π[t+1]没有差别，得到最终的最优策略。

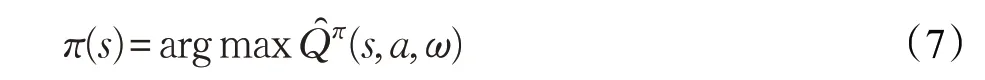
图2 最小二乘策略迭代结构图

基于LSPI的策略学习算法伪代码如算法1所示。

算法1 基于LSPI的策略学习算法

输入：D,ε,ω0

输出：ω

1. 初始化：确定基函数φ，基函数个数k 和折扣因子γ

2. 计算ω：

while ‖ ω-ω' ‖＞ε do

ω ←ω'

for each (s,a,r,s')∈D do

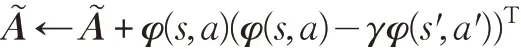
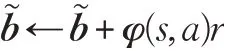
end for

4 基于最小二乘策略迭代的无人机航迹规划

4.1 无人机航迹规划问题的MDP建模

由于LSPI 算法是针对MDP 模型逼近最优策略的一类有效方法，因此先将无人机航迹规划问题建模为MDP 模型。由于无人机在航迹规划过程中，下一时刻的位置只与当前位置和在当前位置采取的动作有关，而与其他信息无关，因此可直接建模为MDP模型。

状态空间为无人机的三维位置集合，动作空间定义为无人机的三维速度集合。回报函数的设计需要考虑各种航迹费用、飞行安全性、UAV的动态约束等航迹性能指标，具体如式（8）所示：

ωh、ωt和ωo分别为各项航迹性能指标的权重系数。在航迹规划问题中所考虑的回报包括连续回报和离散回报两类。

连续回报包括：UAV的飞行高度H= ||Z-Z0，其中Z0为无人机的最佳飞行高度；距离目标位置的距离差：

离散回报为碰撞惩罚；R 为状态转移过程中发生碰撞的惩罚项；C0为UAV与障碍发生碰撞的次数。

4.2 基于LSPI的无人机航迹规划

采样的样本数据形式为(s,a,r,s')，表示在当前状态s 选择动作a 执行后获得回报值r ，同时到达下一状态s' 。当无人机到达目标位置或者发生碰撞时结束单次采样过程。采样阶段结束后，采用LSPI 算法对采集的样本数据进行学习得到最优策略。

基函数的选择是LSPI 算法中一个基本的问题，高斯径向基函数是一种常用的基函数，适用于逼近光滑且连续的函数[17]。函数形式如式（9）所示：

其中μ 表示函数中心，σ 表示函数宽度。

动作的表示是通过复制 ||A 次基函数实现的，基函数大小为 ||ϕ × ||A 。计算选中动作对应的基函数值，其余动作的基函数值都为0，即

其中m 表示基函数个数，l 表示选中的动作a,na表示动作个数。

策略的学习根据算法1所示的伪码进行，学习到策略后，根据策略进行航迹规划，航迹规划伪码如算法2所示。根据学习到的策略估计Q 值，选择Q 值最大的动作执行直到到达目标位置。

算法2 航迹规划算法

输入：s0,sT,ω

输出：Path(s0,sT)

1. 初始化：Path(s0,sT)←{s0}

s ←s0

2. 航迹点计算：

while s ≠sTdo

π=arg max φT(s,a)ω

s′=nextstate(s,π)

s ←s'

Path(s0,sT)←s'

3. 输出Path(s0,sT)

5 仿真结果与分析

通过无人机在复杂城市环境中的航线飞行仿真任务来验证本文航迹算法的有效性。由于针对无人机航迹规划问题暂无标准测试用例，本文设计了包含多种复杂形状障碍的城市场景，如图3所示。任务区域为100 m×100 m×60 m，设计无人机起始点为（15，25，0），目标点为（85，65，35）。航点的到达需要穿越复杂障碍环境，增加了任务的挑战性。为了增加仿真的真实性，采用文献[18]所述四旋翼动力学模型作为仿真中的无人机对象。仿真采用Matlab 软件，由有2.5GHz Core i5-7200U CPU和4 GB RAM的计算机实现。

图3 城市场景抽象图

采用径向基函数对状态进行特征提取，状态特征向量由8 个高斯基函数和1 个常量组成。位置X 分量取{25，65}两个中心点，Y 分量中心点取{25，65}，Z 分量中心点取{15 35}，构成状态空间共8 个高斯基中心点。探索因子γ=0.95。收集的样本数据量为20 000。

由于目前采用与LSPI相关的强化学习方法进行无人机航迹规划的研究较少，因此采用强化学习中应用相对广泛的Q学习算法作为对比算法验证LSPI算法在无人机航迹规划中的有效性。图4 为LSPI 算法与Q 学习算法的实验结果对比图，其中横坐标为情节数，纵坐标表示每一情节对应的运行步数。从图中可以看出，在收敛速度和收敛结果方面LSPI 算法都要优于Q 学习算法，且收敛更加稳定。图5给出了Q学习算法与LSPI算法规划的三维航迹对比图，其中黑虚线为算法规划出的航迹，红实线表示的是将算法规划结果用于UAV 气动模型得到的仿真飞行曲线。具体统计数据见表1。由图5及表1 可知，两种算法都能实现避障，但LSPI 算法的规划时间及航迹长度更短。虽然LSPI算法规划的航迹转弯与起伏动作次数较多，但总的转弯角度和小，转弯幅度小，更利于飞机实际飞行。Q学习算法中采用查询表的形式存储策略，对状态空间进行离散化处理，状态是离散有限的，无人机的位置只能是离散化后的状态空间中的位置，若离散尺度偏大，计算出的航迹点间的距离就较长，无法保证无人机的平滑飞行。LSPI 算法中依据函数逼近器计算策略，函数是连续的，无人机可以到达状态空间中的任意位置，只要动作设置合理，航迹点间的航迹长度就可以保证无人机平滑飞行。

图4 不同算法在不同情节下到达目标所需的时间步

图5 不同算法下的三维航迹对比图

表1 Q-learning与LSPI算法规划结果对比表

总的来说，LSPI算法获得的三维航迹更为平滑，规划时间及航迹长度更短，没有过大的转弯动作，可以节省燃料，提高跟踪精度，更加适合无人机飞行。

6 结束语

本文针对传统Q 学习算法无法有效解决连续状态空间的问题，提出采用基于近似策略表示的最小二乘策略迭代算法进行无人机航迹规划研究。采用线性函数逼近器近似表示动作值函数，利用最小二乘法进行参数更新，根据学习到的参数采用贪心策略进行动作选择。仿真结果表明该算法能有效解决连续状态空间问题，能够为无人机在复杂城市场景中规划出一条从起始位置到目标位置的无碰三维航迹且执行性能较优。

今后的工作将对算法展开进一步测试，并在算法充分训练后在真实的无人机平台实现。