TANGRAM:一个基于比特切片的适合多平台的分组密码*
2020-01-06张文涛季福磊丁天佑杨博翰赵雪锋向泽军包珍珍刘雷波
张文涛,季福磊,丁天佑,杨博翰,赵雪锋,向泽军,包珍珍,刘雷波
1.中国科学院信息工程研究所信息安全国家重点实验室,北京100093
2.中国科学院大学网络空间安全学院,北京100049
3.清华大学微电子学研究所,北京100084
4.湖北大学数学与统计学学院应用数学湖北省重点实验室,武汉430062
5.南洋理工大学,新加坡637371
1 引言
TANGRAM,就是七巧板,它是我们设计的一族新的分组密码算法.TANGRAM的主要设计思想是采用比特切片方法来设计适合多个软硬件平台的系列分组密码,以灵活地适用于多种不同的应用场景.这就像七巧板一样,一套七巧板可以拼出多种不同的图形,这是TANGRAM分组密码得名的原因.
本文在第2节给出TANGRAM的算法描述;第3节给出TANGRAM的设计原则;第4节给出我们对TANGRAM的安全性评估和分析结果;第5节给出TANGRAM在多个软硬件环境下的实现结果;第6节总结TANGRAM的优点和创新点.
2 算法描述
TANGRAM是一族迭代型分组密码算法,用TANGRAM b/k表示分组长度为b比特、密钥长度为k比特的分组密码版本.TANGRAM包括三个版本:TANGRAM128/128,TANGRAM128/256,TANGRAM256/256.为方便起见,按照分组长度的不同,我们将分组长度为128和256比特的TANGRAM分组密码分别记作TANGRAM-128和TANGRAM-256.也就是说,TANGRAM-128包含TANGRAM128/128和TANGRAM128/256两个分组密码,TANGRAM-256指TANGRAM256/256.
TANGRAM的整体结构为SP网络.TANGRAM128/128总轮数为44轮,TANGRAM128/256总轮数为50轮,TANGRAM256/256总轮数为82轮.在加密算法的最后再增加一个子密钥异或操作.每一轮变换包含三个步骤:轮子密钥加AddRoundKey(ARK),列替换SubColumn(SC),行移位ShiftRow(SR).以TANGRAM128/128为例,用Ri表示在轮子密钥Ki作用下的轮变换,m、c分别表示明文和密文,TANGRAM128/128的算法结构如图1所示.
2.1 密码状态和密钥状态
2.1.1 TANGRAM-128状态
将128比特的明文、或128比特的中间状态、或128比特的密文统称为密码状态.令W=w127||···||w1||w0表示一个密码状态,我们用一个4×32的矩形比特阵列表示W,如图2(a)所示,将前32个比特w31||···||w1||w0放在第0行,接下来的32个比特w63||···||w33||w32放在第1行,依次类推.类似地,128比特的轮子密钥也用一个4×32的矩形比特阵列来表示.为了描述方便,以下用二维形式表示TANGRAM-128的密码状态,如图2(b)所示.
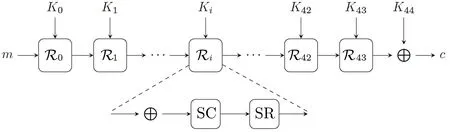
图1 TANGRAM128/128的整体加密过程Figure 1 Encryption process of TANGRAM128/128

图2 TANGRAM-128的密码状态及其二维表示Figure 2 Cipher state and its two-dimensional representation of TANGRAM-128
2.1.2 TANGRAM-256状态
将256比特的明文、或256比特的中间状态、或256比特的密文统称为密码状态.令W=w255||···||w1||w0表示一个密码状态,我们用一个4×64的矩形比特阵列表示W,如图3(a)所示,将前64个比特w63||···||w1||w0放在第0行,接下来的64个比特w127||···||w65||w64放在第1行,依次类推.类似地,256比特的轮子密钥也用一个4×64的矩形比特阵列来表示W.为了描述方便,以下用二维形式表示TANGRAM-256的密码状态,如图3(b)所示.

图3 TANGRAM-256的密码状态及其二维表示Figure 3 Cipher state and its two-dimensional representation of TANGRAM-256
2.2 轮函数变换
2.2.1 轮密钥加AddRoundKey
将128比特(或256比特)的轮子密钥逐比特异或到128比特(或256比特)的密码状态.
2.2.2 列替换SubColumn
对每一列的4个比特做S盒替换.以TANGRAM-128为例,如图4所示,令Col(j)=a3,j||a2,j||a1,j||a0,j(0≤j≤31)表示S盒的输入,S(Col(j))=b3,j||b2,j||b1,j||b0,j表示S盒的输出.
2.2.3 行移位ShiftRow
TANGRAM-128与TANGRAM-256采用不同的移位参数,分别用ShiftRow_128和ShiftRow_256表示.
TANGRAM-128对每一行的32个比特做左循环移位.第0行保持不动,第1行左循环移动1位,第2行左循环移动8位,第3行左循环移动11位.如图5所示,其中⋘x表示左循环移动x位.

表1 TANGRAM的S盒真值表Table 1 Truth table of TANGRAM S-box

图4 TANGRAM-128列替换操作Figure 4 SubColumn operation of TANGRAM-128
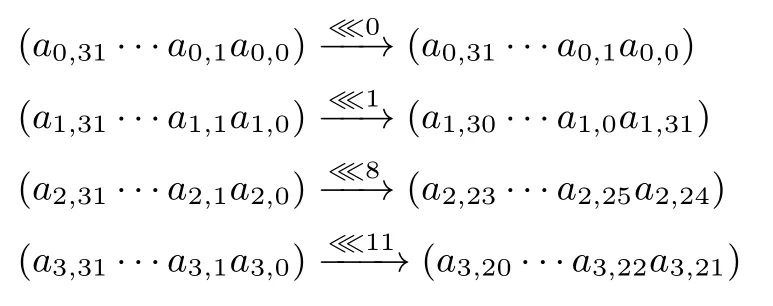
图5 TANGRAM-128行移位操作Figure 5 ShiftRow operation of TANGRAM-128
TANGRAM-256对每一行的64个比特做左循环移位.第0行保持不动,第1行左循环移动1位,第2行左循环移动8位,第3行左循环移动41位.
2.3 密钥扩展
2.3.1 TANGRAM128/128密钥扩展
将128比特的种子密钥V=v127||···||v1||v0用一个4×32的矩形比特阵列表示,如图6所示.

图6 TANGRAM128/128密钥状态及其二维表示Figure 6 Key state and its two-dimensional representation of TANGRAM128/128
令Rowi=ki,31||···||ki,1||ki,0表示第i行,0≤i≤3,Rowi可以看作一个32比特的字.在第r(r=0,1,···,43)轮,先提取128比特的子密钥,轮子密钥Kr=Row3||Row2||Row1||Row0;然后,128比特的密钥状态做以下更新:
(1)对密钥状态进行S盒操作(与加密算法中的S盒相同),即:
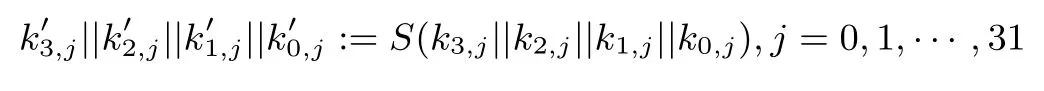
(2)进行一轮的4分支广义Feistel变换,如下:
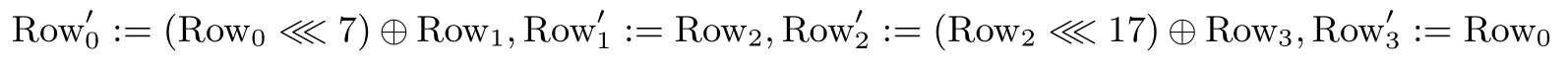
(3)将6比特的轮常数RC[r](r=0,1,···,43)与密钥状态第一行的6个比特(k0,5||k0,4||k0,3||k0,2||k0,1||k0,0)进行异或.轮常数RC[r](r=0,1,···,43)的生成方法见2.3.2节.
将上面三个步骤的复合变换记为UpdateRC[r][X],其中X为128比特.在第43轮的密钥状态更新之后,将更新的密钥状态的值赋给K44.
2.3.2 TANGRAM128/256密钥扩展
将256比特的种子密钥分成左右两半部分,K=KL||KR,其中KL和KR都是128比特.利用Feistel网络,TANGRAM128/256所需的51个128比特的子密钥生成如下:

轮常数RC[r](r=0,1,···,48)由一个6比特的线性反馈移位寄存器生成.用(rs5,rs4,rs3,rs2,rs1,rs0)表示反馈寄存器的状态,在每一次更新时,将状态左移动1位,并将rs0更新为rs5⊕rs4,初始值RC[0]:=0x1.
2.3.3 TANGRAM256/256密钥扩展
将256比特的种子密钥V=v255||···||v1||v0用一个4×64的矩形比特阵列表示,如图7所示.

图7 TANGRAM256/256密钥状态及其二维表示Figure 7 Key state and its two-dimensional representation of TANGRAM256/256
令Rowi=ki,63||···||ki,1||ki,0表示第i行,0≤i≤3,Rowi可以看作一个64比特的字.在第r(r=0,1,···,81)轮,256比特的轮子密钥Kr=Row3||Row2||Row1||Row0.提取出轮子密钥Kr之后,密钥状态做以下更新:
(1)对密钥状态进行S盒操作(与加密算法中的S盒相同),即:
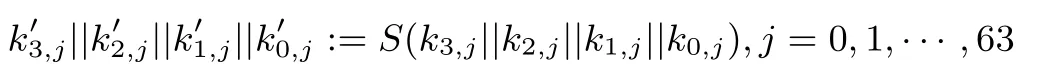
(2)进行一轮的4分支广义Feistel变换,如下:

(3)对密钥状态的第一行的7个比特(k0,6||k0,5||k0,4||k0,3||k0,2||k0,1||k0,0),异或7比特的轮常数RC[r](r=0,1,···,81).
最后,将更新的密钥状态的值赋给K82.
轮常数RC[r](r=0,1,···,81)由一个7比特的线性反馈移位寄存器生成.用(rs6,rs5,rs4,rs3,rs2,rs1,rs0)表示反馈寄存器的状态,在每一次更新时,将状态左移动1位,并将rs0更新为rs6⊕rs5,初始值为RC[0]:=0x1.
3 设计原理
3.1 TANGRAM的整体设计原则
安全性:密码算法的第一要素是安全性.对于一个分组长度为n、密钥长度为k的分组密码,如果不存在一种攻击方法有比2n少得多的数据复杂度并且比2k少得多的时间复杂度,就称此分组密码是安全的.通常用一个分组密码的安全冗余来评价其安全强度.设分组密码的总轮数为R,如果最多可以攻击到R-m轮的缩减轮密码,就称该分组密码具有m轮的绝对安全冗余,或者具有m/R的相对安全冗余.安全冗余反映了一个分组密码抵抗现有的安全性分析方法的安全强度.
实现性能:密码算法的第二要素是实现性能,即在特定平台上进行加密运算或者解密运算所需要的资源.在硬件实现中,通常用实现面积和吞吐量来衡量;在软件实现中,通常用加密速度、代码量和内存占用来衡量.处理器字长和指令集的差异,会让一个密码算法的性能在一些平台上表现优秀、而在另外一些平台上表现很差.考虑到一个分组密码具有多种多样的应用场合,我们在设计TANGRAM时,兼顾硬件和软件实现,尽可能地使TANGRAM在多个平台上都具有不错表现.
简单性:一个简单的密码算法,由于其描述和运算的简单性,会利于正确无误的实现,也会吸引更多人对其安全性和实现性能的关注,进而对该密码算法建立更强的信任感.因此,简单性是我们设计TANGRAM的一项原则.
3.2 TANGRAM轮函数的设计
TANGRAM的设计基于比特切片方法[1],整体结构为SP网络.考虑一个分组长度为128比特或256比特的SP型分组密码,设S层由32个或64个4×4的S盒并置构成.因而在比特切片的实现中,子块的长度为32比特或64比特.将128比特或256比特的密码状态用一个4×32或4×64的比特阵列表示,S层对每一列独立地进行相同的S盒替换,那么,接下来的P变换应该让输出的每一列依赖于其它一些列,以提供必要的扩散性.我们选择了对每一行的32比特字或64比特字进行循环移位操作:循环移位在硬件上可以用简单的拉线实现;能够达到每一列依赖于其它一些列的目的;比特切片实现时,循环移位在软件上可以很容易的高效实现.至此,我们得到了TANGRAM轮函数的基本框架.
得益于我们对S盒的细致选取(详见3.3节),TANGRAM达到了很好的安全性和实现性能的平衡;P置换的设计也非常重要(详见3.4节),它仅由三个32比特字或64比特字上的循环移位组成,不仅能提供必要的扩散性,也兼顾了硬件和软件的实现性能.TANGRAM的S盒层和P置换层组合在一起,所形成的密码算法整体具有很好的抵抗差分/线性攻击,这也在很大程度上提高了TANGRAM的安全性和实现性能之间的性价比.
3.3 TANGRA M的S盒设计
3.3.1 相关定义和定理
定义1令S表示一个4×4的S盒,对任意△I,△O∈,定义NDS(△I,△O)为:

定义2 (差分均匀度)令S表示一个4×4的S盒,定义S的差分均匀度Diff(S)为:
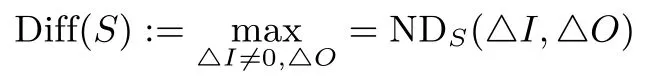
定义3令S表示一个4×4的S盒,对任意ΓI,ΓO∈,定义Im bs(ΓI,ΓO)为:
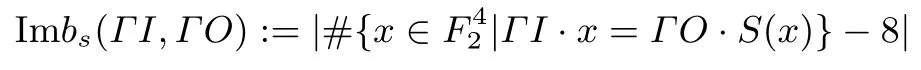
定义4 (线性度)令S表示一个4×4的S盒,定义S的线性度Lin(S)为:
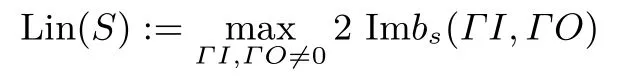
对于任意4×4的双射S盒,均有Diff(S)≥4并且Lin(S)≥8,使得这两个值都达到最小值的S盒被称为最优S盒.
定义5 (最优S盒[2])令S表示一个4×4的S盒,称S是最优S盒,若它满足以下三个条件:
(1)S是双射的;
(2)Diff(S)=4;
(3)Lin(S)=8.
定义6 (SetD1S和CarD1S)令△I∈表示一个非零输入差分,△O∈表示一个非零输出差分.令wt(x)表示x的比特汉明重量.定义SetD1S为:
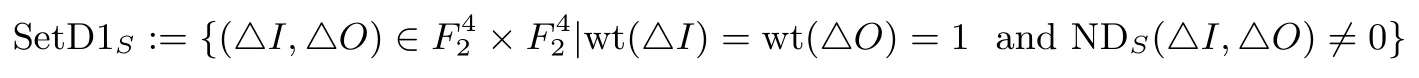
令CarD1S表示集合SetD1S的势.
定义7 (SetL1S和CarL1S)令ΓI∈表示一个非零输入选取模式(也称为输入掩码),ΓO∈表示一个非零输出选取模式(也称为输出掩码).定义SetL1S为:
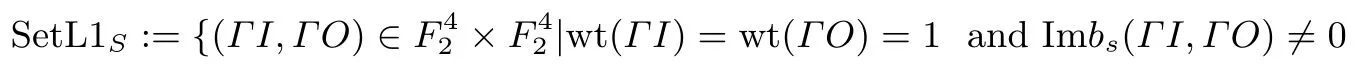
令CarL1S表示集合Set L1S的势.
定义8 (仿射等价[2])两个4×4的S盒S和S′被称为仿射等价,如果存在双射的线性映射A,B以及常数a,b∈,满足
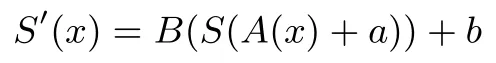
若两个S盒S和S′仿射等价,则有Diff(S)=Diff(S′)和Lin(S)=Lin(S′).也就是说,S盒的差分均匀度和线性度在仿射变换下是不变量.
定理1[2]令S和S′是两个仿射等价的S盒.若S是最优S盒,则S′也是最优S′盒.
定义9 (置换异或等价permutation-then-XOR equivalent[2])两个4×4的S盒S和S′被称为置换异或等价,如果存在F2上的4×4置换矩阵P0,P1以及常量a,b∈,满足
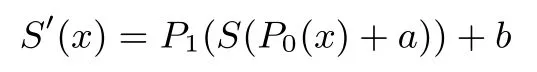
我们简称这种等价为PE等价(PE equivalence).若两个S盒PE等价,则它们一定仿射等价.
定义10 (分量布尔函数)令S表示一个4×4的S盒.对于任意的b∈,如下定义S的分量布尔函数Sb:

3.3.2 S盒的选取
TANGRAM采用了4比特S盒,设计准则如下:
(1)S是双射的,即对任意x/=x′,有S(x)/=S(x′);
(3)CarD1S=2;
(5)CarL1S=2;
一个S盒若满足准则(1)、(2)和(4),那么它是最优的S盒,并且任意一个与之仿射等价的S盒也满足准则(1)、(2)和(4)(见定义8和定理1).一个S盒若满足准则(1)~(5),那么,任意一个与之PE等价(见定义9)的S盒也满足准则(1)~(5).
根据定理1,所有的最优S盒可以通过仿射等价关系划分等价类.实际上,所有的最优4比特S盒只存在16种不同的仿射等价类[2].利用文献[2]中给出的16个仿射等价类的代表元,我们设计了一个算法将所有满足准则(1)~(5)的4比特S盒划分成PE等价类,结果显示满足条件的只有4个PE类.表2给出了这4个PE类的代表元,其中,每一行中,第一个数代表输入为0的S盒的输出,第二个数代表输入为1的S盒的输出,依次类推.

表2 满足准则(1)~(5)的4个PE类的代表元Table 2 Representatives for all 4 PE classes fulfi lling criteria(1)~(5)
如果一个S盒满足准则(1)~(5),那么给它的输入变量或者输出变量异或一个常数,所得到的新S盒仍然满足准则(1)~(5),并且也不会改变相应密码算法的最优差分迹的概率和最优线性迹的相关系数(差分迹及其概率、线性迹及其相关系数,详见第4节的安全性分析).因此,我们只需考虑表1中的4个代表元所生成的4×4!×4!=2304个S盒,用{Si:i=0,1,···,2303}来表示这2304个S盒.
首先,利用文献[3]中的算法2,能够删除掉一部分会导致每轮只有一个差分(或者线性)活跃S盒的候选S盒.总共有1776个S盒被删除,只剩下528个候选S盒.接下来,我们通过考查相应密码算法抵抗差分和线性密码分析的安全性来对这528个S盒做进一步筛选.令ProbD25表示最优25轮差分迹的概率,表示最优25轮线性迹的相关势(相关势的定义见第4节的安全性分析).固定P置换ShiftRow_128,对于528个候选S盒中的每一个,检验相应的128比特分组长度下的密码算法是否满足以下两个不等式:ProbD25<2-128和实验结果表明,528个S盒中,有124个S盒满足前者不等式;而在这124个S盒中,又有36个满足后者不等式.根据ProbD25和的值,这36个S盒被划分成2组,表3给出了ProbD25和的值以及对应S盒的个数.

表3 32个候选S盒分成2个组Table 3 Divide 32 candidate S-boxes into two groups
在这两组S盒中,由于第1组的最优25轮线性迹相关势更高,我们选择了第1组的28个S盒进行256比特版本密码算法的测试.固定P置换ShiftRow_256,对于28个候选S盒中的每一个,我们搜索其在相应的256比特分组长度下的密码算法的最优差分迹与最优线性迹.结果表明49轮的最优差分迹概率和最优线性迹相关势均小于2-256.
我们选取了第1组S盒中的第1个S盒.通过在这个S盒变换的前后各加一个常数,可以得到16×16=256个PE等价的S盒.在这256个S盒中,我们选择了一个没有不动点、并且软件实现速度和硬件面积需求均有较好表现的S盒作为TANGRAM的S盒.
3.4 TANGRAM的扩散层设计
扩散层的设计旨在提供扩散性,使输出的每一列依赖于输入的一些列.我们所选的设计是对每一行的32个比特或64个比特做左循环移位,令ci(i=0,1,2,3)表示对第i行左循环移位的参数,这些参数的选取准则如下:
(1)c0=1,c1=1,c2=8,c2<c3;
(2)达到全扩散所需的轮数最少.
注:考虑到在一些低端处理器上,循环左移的参数选为1和8时更为高效,因此我们选取了c1=1且c2=8.
对于TANGRAM-128,我们的实验结果表明,共有5组候选参数满足以上准则,经过6轮的轮函数变换之后,128个输入比特中的每个比特都会影响到128个输出比特中的每个比特.从这5种候选参数中,我们选取了(c1,c2,c3)=(1,8,11)作为ShiftRow的循环移位参数.
对于TANGRAM-256,我们的实验结果表明,共有13组候选参数满足以上准则,经过8轮的轮函数变换之后,256个输入比特中的每个比特都会影响到256个输出比特中的每个比特.从这13种候选参数中,我们选取了(c1,c2,c3)=(1,8,41)作为ShiftRow的循环移位参数.
3.5 TANGRAM的密钥扩展算法设计
TANGRAM的密钥扩展算法设计准则如下:
(1)共用加密算法中的S盒,减少实现代价;
(2)扩散层使用了广义Feistel结构,增加其扩散性;
(3)使用轮常数消除对称性.
TANGRAM的密钥扩展算法满足以上设计准则.通过一些初步分析,我们相信TANGRAM能够抵抗与密钥扩展算法有关的攻击
4 安全性分析
4.1 TANGRAM安全性概述和声明
TANGRAM128/128的总轮数为44轮,根据我们的安全性分析和评估结果,我们最多能攻击到28轮(占全部轮数的63.6%).因此,TANGRAM128/128的绝对安全冗余为16轮,相对安全冗余为36.4%.
6轮TANGRAM-128达到全扩散,因此我们在44轮的基础上又增加了6轮,将50轮作为TANGRAM128/256的总轮数.根据我们对28轮TANGRAM128/128的差分攻击结果,我们估计,对TANGRAM128/256最多能攻击到30轮(占全部轮数的60%).因此,TANGRAM128/256的绝对安全冗余为20轮,相对安全冗余为40%.
TANGRAM256/256的总轮数为82轮,我们估计最多能攻击到56轮(占全部轮数的68%).因此,TANGRAM256/256的绝对安全冗余为26轮,相对安全冗余为32%.
我们认为:以当前分组密码分析方法的发展现状作为参考,我们为TANGRAM的3个版本预留的冗余都足够保证其抵抗数学类攻击的安全性.
4.2 TANGRAM抵抗差分密码分析的安全性
利用差分密码分析方法[4,5]攻击一个分组长度为n比特的R轮分组密码,需要找到一个R-w轮的、并且概率大于21-n的差分传播,w的取值和具体分组密码有关.差分迹也称为差分特征.一个差分传播是若干差分迹的集合,集合中的差分迹具有相同的输入差分和相同的R-w轮变换后的输出差分,差分传播的概率是集合中所有差分迹的概率之和.
基于我们提出的搜索算法[6],我们搜索了128比特分组长度下TANGRAM的第1-26轮的最优差分迹和256比特分组长度下TANGRAM的第1-50轮的最优差分迹,结果如表4和表5所示.
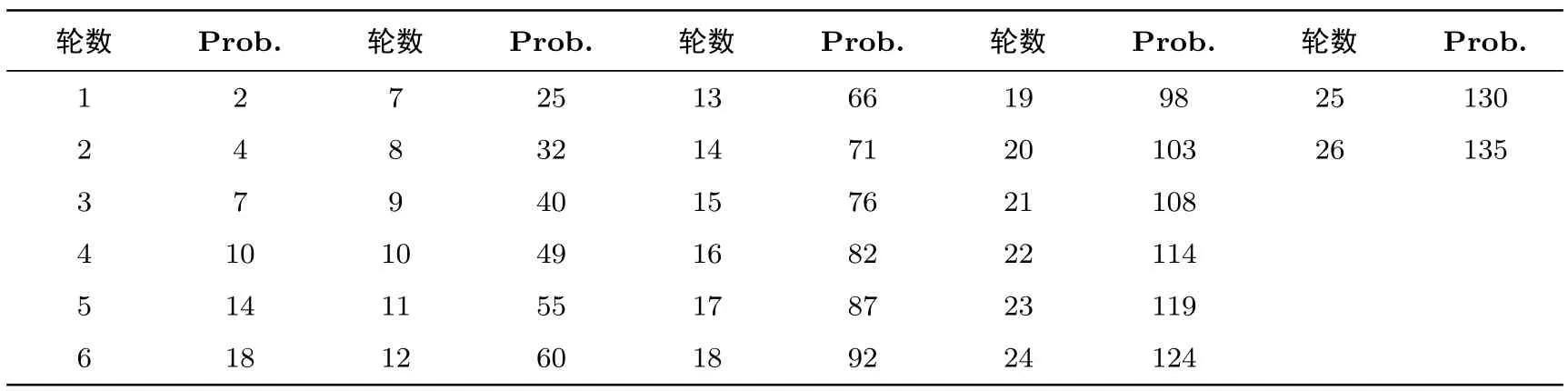
表4 TANGRAM-128最优差分迹概率Table 4 Probabilities of the best differential trails of TANGRAM-128
从表4可以看到,128比特分组长度下TANGRAM的25轮最优差分迹的概率为2-130,小于边界值2-127;从表5可以看到,256比特分组长度下TANGRAM的49轮最优差分迹的概率为2-258,小于边界值2-255.
TANGRAM扩散层的设计非常简单,因此需要考虑TANGRAM差分/线性迹的聚集效应.TANGRAM和RECTANGLE在设计上具有相似性.我们对RECTANGLE差分迹的聚集效应进行了深入研究和实验验证,结果表明:RECTANGLE差分迹的聚集效应非常有限,即使利用聚集效应,也不能构造出轮数更长的差分区分器.可以推断:TANGRAM同样具有非常有限的差分迹聚集效应.RECTANGLE的分组长度为64比特,而TANGRAM的分组长度为128或256比特,因此受限于计算机的处理能力,对TANGRAM差分/线性迹聚集的实验在实际中几乎不可行.我们为TANGRAM预留了足够的安全冗余,因此我们相信三个版本的TANGRAM分组密码均足以抵抗差分密码分析.
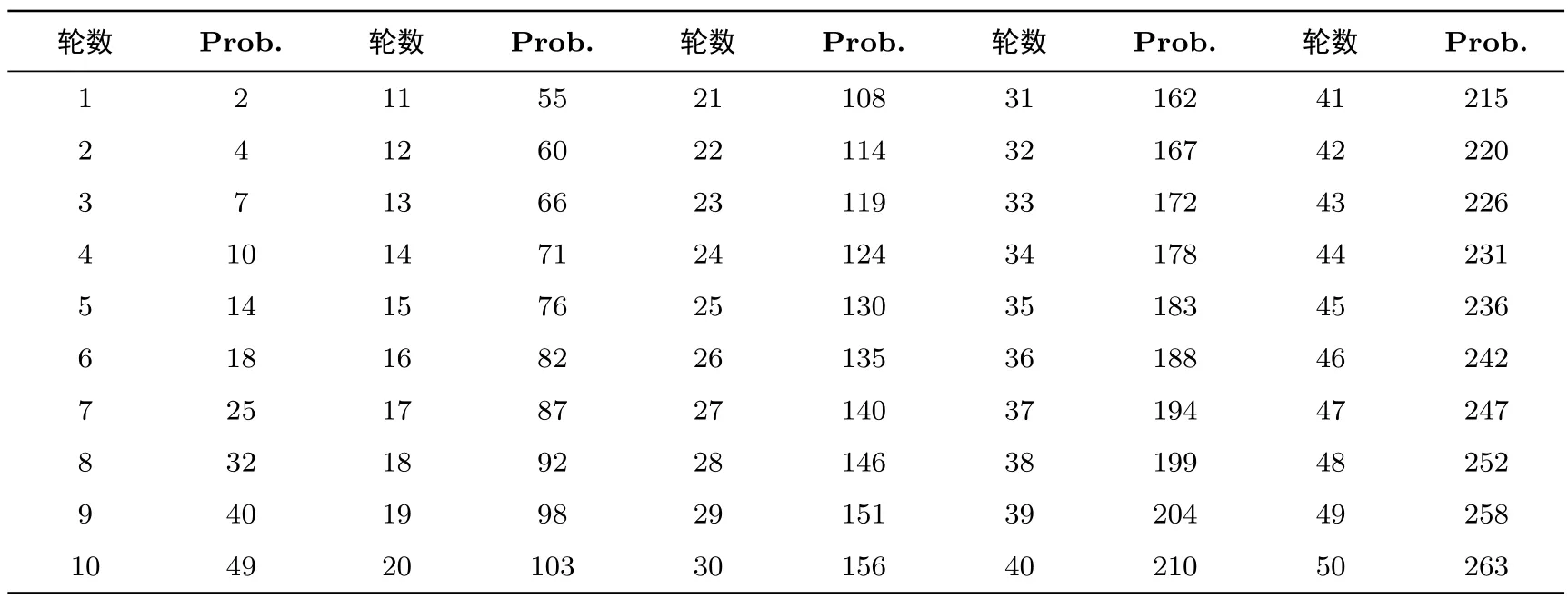
表5 TANGRAM-256最优差分迹概率Table 5 Probabilities of the best differential trails of TANGRAM-256
4.3 对缩减轮TANGRAM的差分攻击
利用TANGRAM-128的一个概率为2-124的24轮差分迹,我们给出了一个对28轮TANGRAM128/128的差分攻击.攻击的数据复杂度为2126.68个明密文对,存储复杂度为2120个密钥计数器,时间复杂度大约为2122.5次28轮加密,成功率大约为82%.
对TANGRAM128/128,在我们所考虑的安全性分析方法中,上面对28轮的差分攻击,是能攻击到的最长轮数.根据这个攻击,我们估计,对TANGRAM128/256,最多能攻击到30轮.
4.4 TANGRAM抵抗线性密码分析的安全性
令一个线性迹(也称为线性逼近,或者线性特征)成立的概率为p,定义它的偏差ε为(p-1/2),相关系数C为2ε.利用线性密码分析方法[7,8]攻击一个分组长度为n比特的R轮分组密码,需要找到一个R-u轮的、并且相关系数的绝对值大于2-n/2的线性传播,u的取值和具体分组密码有关.一个线性传播是若干线性迹的集合,集合中的线性迹具有相同的输入选取模式和相同的R-u轮变换后的输出选取模式,线性传播的相关系数是集合中所有线性迹的相关系数之和.线性迹的相关系数带有正负号,是正号还是负号,这和子密钥的取值有关.
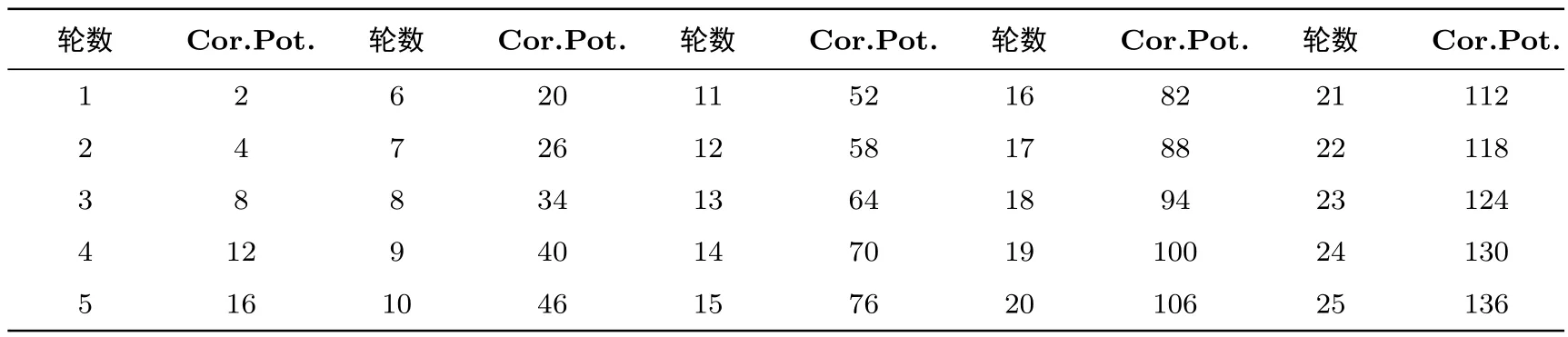
表6 TANGRAM-128最优线性迹的相关势Table 6 Correlation potentials of the best linear trails of TANGRAM-128
修改最优差分迹的搜索算法,我们搜索了128比特分组长度下TANGRAM的第1-25轮的最优线性迹和256比特分组长度下TANGRAM的第1-29轮的最优线性迹,结果如表6和表7所示.
从表6可以看到,24轮的最优线性迹的相关势为2-130,小于边界值2-128;由于计算能力所限,256比特分组长度的最优线形性迹只跑到29轮,但根据表7所呈现的规律:从第8轮开始,每增加一轮,则线性相关势的重量增加了6,因此,可以推断46轮的最优线性迹的相关势为2-262,小于边界值2-256.
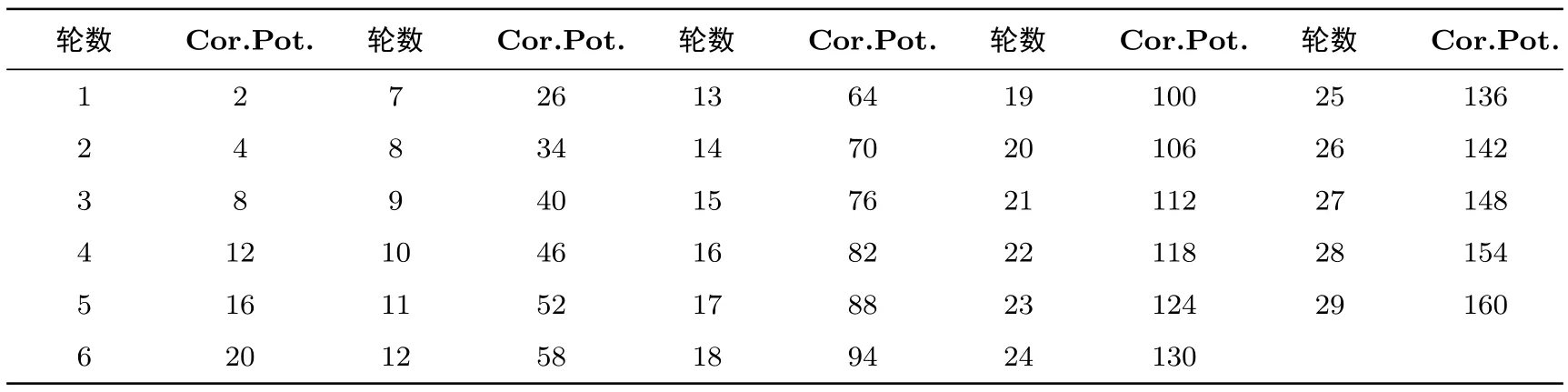
表7 TANGRAM-256最优线性迹的相关势Table 7 Correlation potentials of the best linear trails of TANGRAM-256
我们对RECTANGLE线形迹的聚集效应进行了深入研究和实验验证,结果表明:RECTANGLE线形迹的聚集效应也非常有限.同样,可以推断:TANGRAM也具有非常有限的线性迹聚集效应.考虑到我们为TANGRAM预留的安全冗余,我们相信三个版本的TANGRAM分组密码均足以抵抗线性密码分析.
4.5 TANGRAM抵抗不可能差分密码分析的安全性
不可能差分密码分析[9]利用概率为0的差分传播,这种差分传播一般通过中间相遇方法构造.根据不可能差分密码分析的研究现状,一个分组密码的最长不可能差分区分器的轮数接近于全扩散轮数的两倍.
比如,RECTANGLE的全扩散轮数是4轮,我们能找到的它的最长不可能差分区分器的轮数是8轮.
由于TANGRAM-128和TANGRAM-256的全扩散轮数分别是6轮和8轮,因此我们预估它们的最长不可能差分区分器的轮数大约为12轮和16轮,这与相应TANGRAM版本的的总轮数相差很大.因此TANGRAM的三个版本均具有足够的抵抗不可能差分密码分析的安全性.
4.6 TANGRAM抵抗积分密码分析的安全性
积分密码分析(也称为平方攻击,饱和攻击)[10,11]关注的是多个数据之和的传播性质,积分区分器的概率也为1.可分性[12]是近几年提出的一种一般化积分性质,利用可分性可以构造较传统方法更长更精确的积分区分器.我们将采取基于混合整数线性规划的技术[13]搜索TANGRAM系列算法的积分区分器.
搜索结果显示:TANGRAM-128存在12轮积分区分器,并且在混合整数线性规划的搜索框架下不存在13轮积分区分器;TANGRAM-256存在16轮积分区分器,但是受限于计算资源,我们无法确定TANGRAM-256是否存在17轮积分区分器.虽然搜索算法无法返回TANGRAM-256的17轮结果,但是基于可分性在其它分组密码上的应用,我们相信TANGRAM-256的积分区分器应该不超过20轮.
TANGRAM-128的12轮积分区分器:固定TANGRAM-128最左边S盒的4比特为任意常数,遍历剩下的124比特得到一组包含2124个数据的明文集,将该集合加密12轮后所有输出的异或在w3,20和w3,9处取值恒为零.TANGRAM-256的16轮积分区分器:固定TANGRAM-256最左边S盒的高位比特(即w3,61)为任意常数,遍历剩下255比特得到一组包含2255个数据的明文集,将该集合加密16轮后所有输出的异或在w3,61处取值恒为零.
同样,我们构造出的可分积分区分器的轮数和相应TANGRAM版本的总轮数相差很大.因此TANGRAM的三个版本均具有足够的抵抗积分密码分析的安全性.
4.7 抗相关密钥密码分析
在利用密钥扩展算法的攻击中,最有效的是滑动攻击[14,15]和相关密钥攻击[16].对于TANGRAM,在密钥扩展算法中嵌入不同的轮常量可以阻止滑动攻击;类似于加密算法中的S盒层的使用,给密钥扩展算法提供足够的混淆性;一轮广义Feistel网络可以提供适合的扩散性.基于上述考虑,我们相信,TANGRAM不存在弱密钥、等价密钥,对密钥的选择没有限制,其三个版本均具有足够的抵抗密钥扩展类攻击的安全性.
4.8 抗代数攻击
代数攻击应用于分组密码的成功例子非常罕见.TANGRAM的S盒没有特殊的代数结构.因此,我们相信代数攻击对TANGRAM的安全性没有任何威胁.
5 软硬件性能分析
5.1 在X64平台的软件实现
5.1.1 测试环境说明
测试的硬件环境是一台个人计算机,具有3.40 GHz的Intel(R)Core(TM)i7-6700 CPU,16.0 GB的内存.软件环境是64位Windows 10操作系统,使用Microsoft Visual Studio 2010 Professional Edition,Intel C/C++编译器.在所有测试数据中,测试消息的长度为2 KB,cpb表示cycles per byte,Mbps表示Mbits per second.
5.1.2 测试结果
对TANGRAM的三个版本,我们进行了ECB、CBC和CTR三种工作模式下的基本实现和SSE/AVX指令集的优化实现.
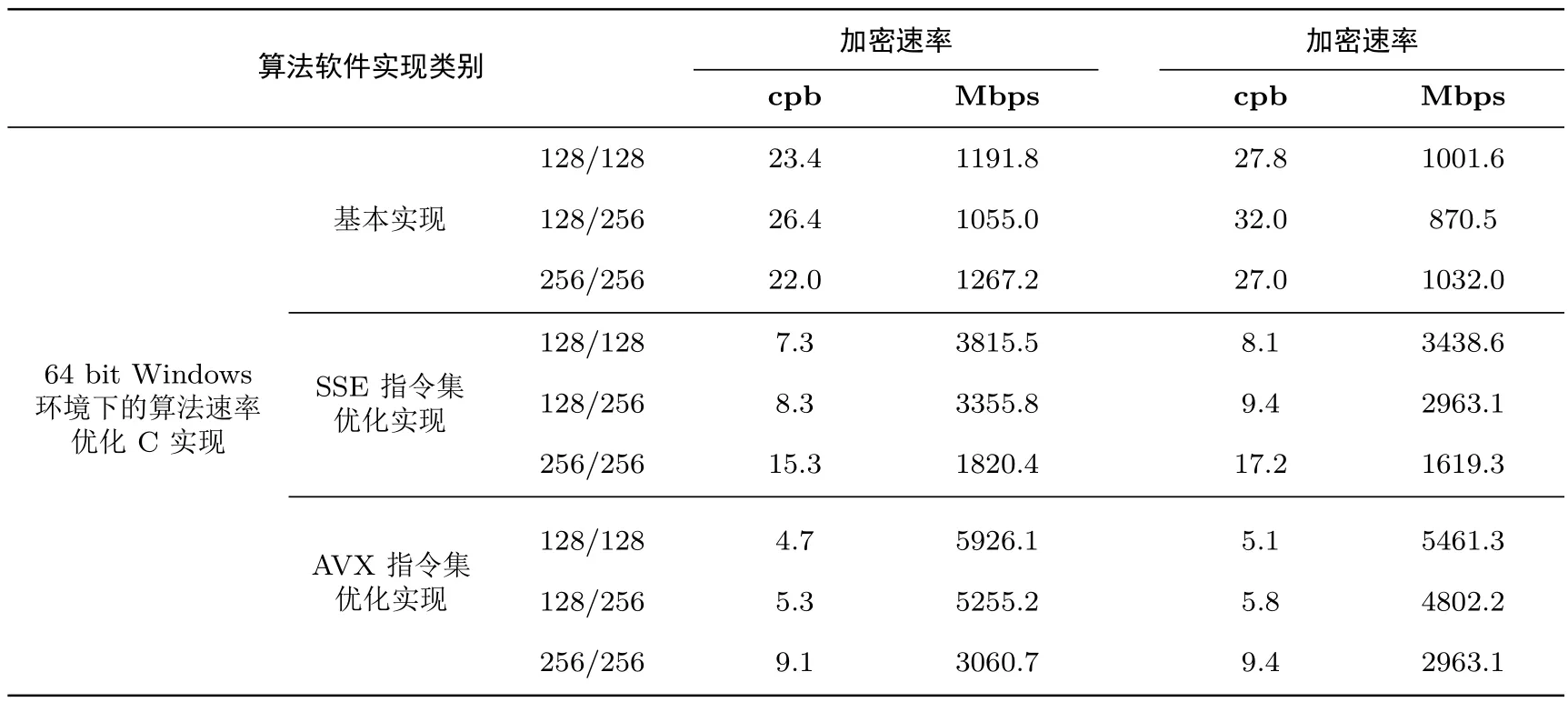
表8 ECB模式速度测试结果Table 8 Software implementation speed in ECB mode
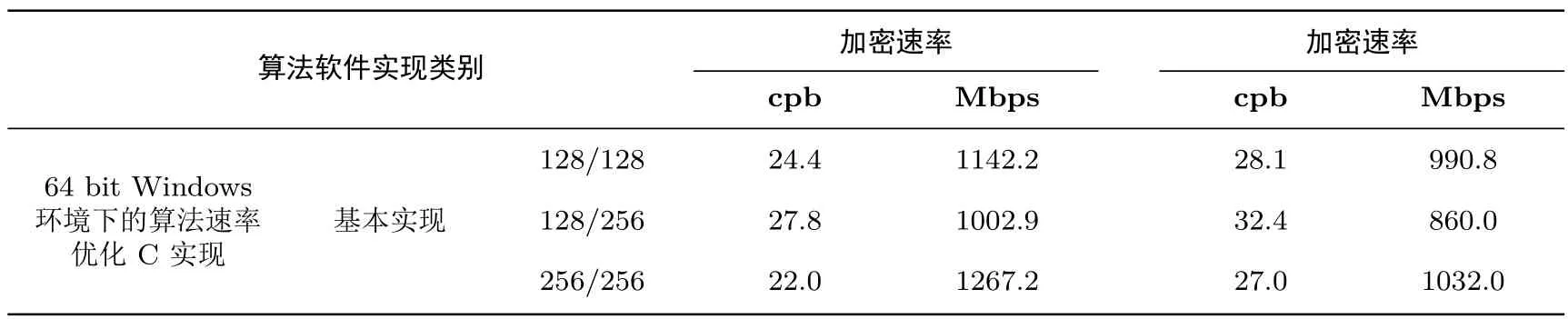
表9 CBC模式速度测试结果Table 9 Software implementation speed in CBC mode
利用SSE指令集,对于TANGRAM-128,每次完成4个分组块的并行运算;对于TANGRAM-256,每次完成2个分组块的并行运算.利用AVX指令集,对于TANGRAM-128,每次完成8个分组块的并行运算;对于TANGRAM-256,每次完成4个分组块的并行运算.由于TANGRAM的设计基于比特切片技术,以上数据格式转换的开销非常低(使用(v)punpck系列指令实现).
表8-表10列出了我们的测试结果.可以看出,利用SSE和AVX指令集,TANGRAM的软件实现速度得到了数倍的提升.
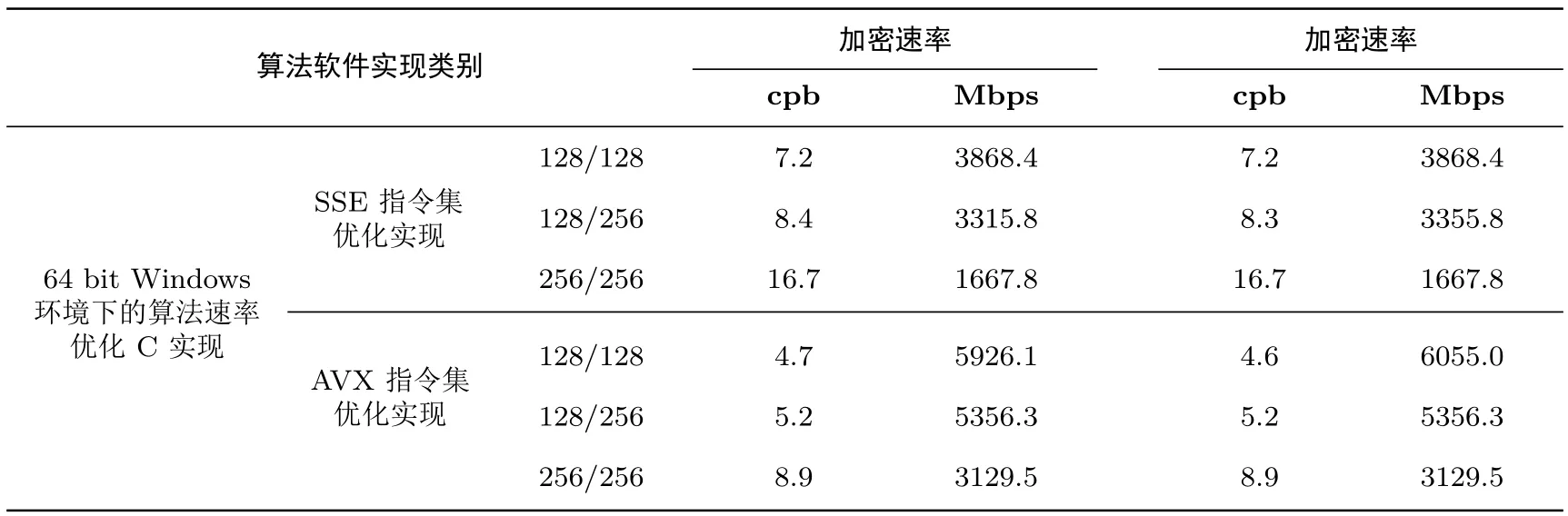
表10 CTR模式速度测试结果Table 10 Software implementation speed in CTR mode
5.2 在32位ARM Cortex-M3平台的软件实现
在32位ARM Cortex-M3平台的实现,采用Keil5+Jlink进行编译调试,性能测试采用Keil5软件记录时间,通过比较执行代码片段前后的时间差得到运行时间.ARM平台拥有丰富的指令集,使用如多内存加载、循环移位、逻辑运算、字节交换等指令可以非常方便地实现TANGRAM算法.具体测试结果如表11所示,我们给出了两种不同速度单位分别在C语言和汇编语言下的测试结果,cpb(cycles per byte)由设备频率72 MHz换算而来.
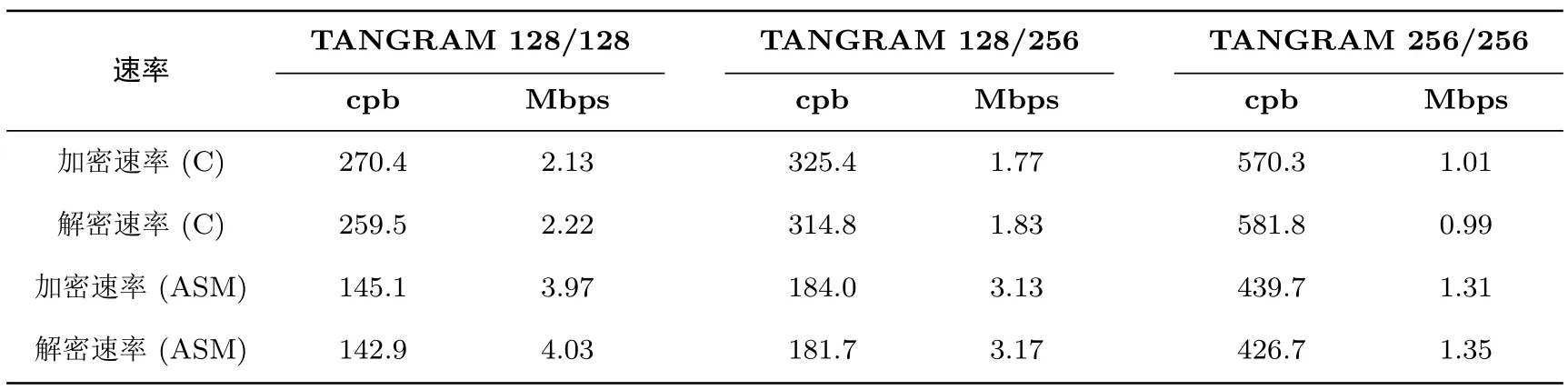
表11 32位ARM环境下的算法速率优化C实现速度测试结果Table 11 Speed-optimized C implementation results on 32-bit ARM
此外,NEON是适用于ARM Cortex-A系列处理器的一种128位SIMD(single instruction,multiple data,单指令、多数据)扩展结构.类似于Intel处理器中的SSE指令,利用NEON指令集可以更大幅度地提升TANGRAM在ARM平台的加解密速度.
5.3 在8位AVR平台的软件实现
为了评估TANGRAM在8位微控制器上的性能,我们进行了针对Atmel AVR 8位微处理器的软件实现.具体的目标设备是ATmega128,其上配有128 KBytes的闪存(fl ash,即只读内存ROM),4 KBytes的随机存储内存(RAM),以及32个8比特通用寄存器.实现所考虑的应用场景包括:
(1)使用CBC模式加/解密128字节消息.这种应用场景对应于传感器网络和IoT设备之间的安全通信.
(2)使用CTR模式加密一个分组块的消息(128比特或256比特).这种应用场景对应于IoT认证所需执行的挑战-握手认证协议.
实现所使用的是汇编代码,并使用Atmel Studio 7.0中所带有的AVR macro assembler进行编译.我们关注以下三个方面:ROM开销(以字节Bytes记),RAM开销(以字节Bytes记),执行时间(以cycles记),以及执行速度(以cycles/byte记).表12-表15汇总了我们的测试结果.
由测试结果可以看出,对于128比特分组长度的TANGRAM,当考虑第一种应用场景(CBC模式加密解密128字节数据),其可以在不损失运行时间的情况下花费极小的代码量(ROM);对于所考虑的第二
种应用场景(CTR模式执行认证握手协议处理较短数据),其只需要可忽略的随机存储内存(RAM).实际上,第一种应用场景中几乎全部的RAM是用来存储扩展出来的轮子密钥;类似地,在第二种应用场景下很大一部分的ROM需求是用来存储扩展出来的轮子密钥,而加密解密部分所需的代码量和随机存储内存(ROM和RAM)都非常少.对于256比特分组长度的TANGRAM,由于状态大到无法全部存放于寄存器上进行更新,我们需要将一半的状态存储于RAM中,这不仅需要额外的RAM开销,而且需要不断地从RAM中装载和暂存一半的状态字节,这导致执行时间也有了不容忽视的额外开销,因而相较于128比特分组长度的版本,256比特分组长度的版本不是很适合在资源受限的低端微处理器上实现.

表12 TANGRAM在8位AVR平台的测试结果(CBC模式下的加密算法)Table 12 Results on 8-bit AVR platform(encryption speed in CBC mode)
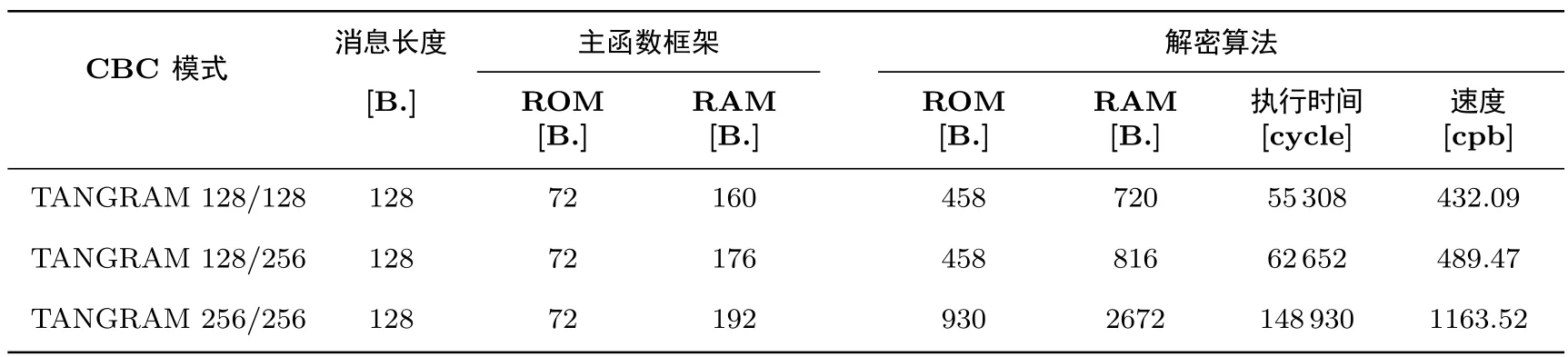
表13 TANGRAM在8位AVR平台的测试结果(CBC模式下的解密算法)Table 13 Results on 8-bit AVR platform(decryption speed in CBC mode)
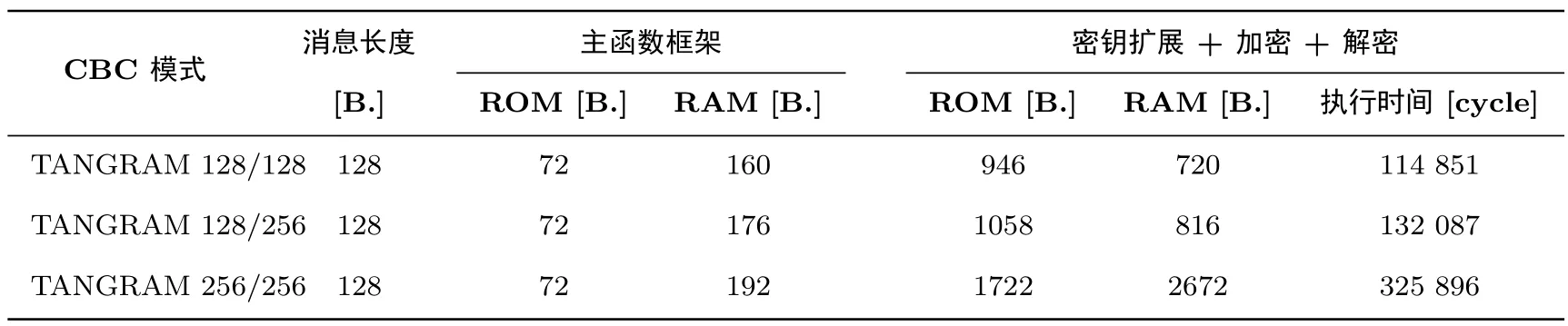
表14 TANGRAM在8位AVR平台的测试结果(CBC模式下的密钥扩展+加密+解密)Table 14 Results on 8-bit AVR platform(speed of combination of key-schedule+encryption+decryption in CBC mode)
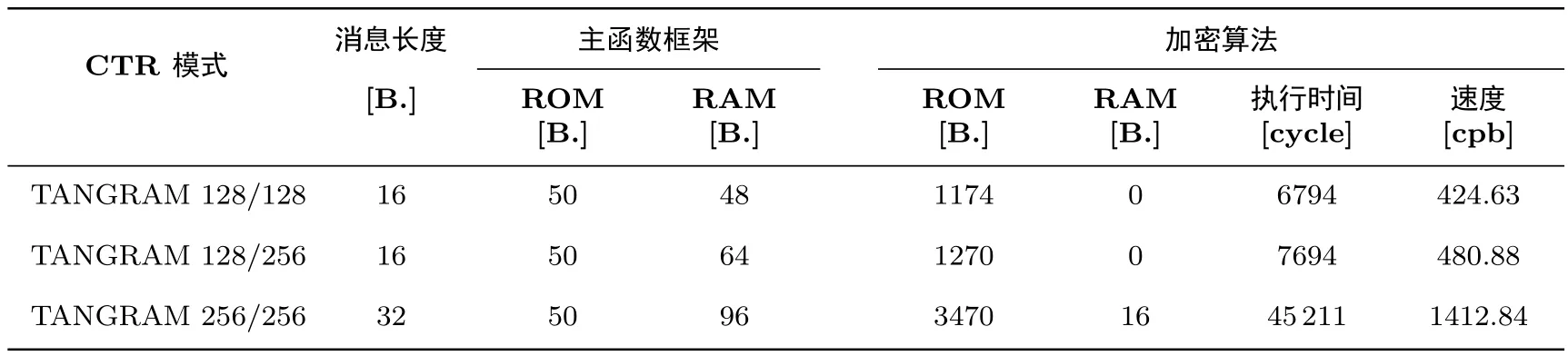
表15 TANGRAM在8位AVR平台的测试结果(CTR模式)Table 15 Results on 8-bit AVR platform(in CTR mode)
5.4 硬件实现
为了评估TANGRAM的硬件实现性能,我们针对两类硬件实现平台进行评估,即专门应用的集成电路(ASIC)和可编程逻辑阵列(FPGA).我们选取了两个常见的工艺库来评估ASIC硬件实现:UMC 130 nm和学术界常用的开源工艺库Nangate 45 nm.Xilinx公司的7系xc7s100fgga676-1FPGA平台被用来评估TANGRAM在FPGA上的实现结果和性能.
我们准备了可用于ECB模式的TANGRAM三个版本的硬件实现.除此之外,为了说明TANGRAM算法硬件实现的灵活性,我们同时提供了基于CTR模式的纯加密模块的轻量级实现和高速实现.
我们采用了多种优化方式来实现TANGRAM的ECB模式.如图8所示,其中加解密算法共享多个基本模块单元,包括轮子密钥加、轮状态、密钥存储等.对于TANGRAM128/256版本,因为密钥扩展算法采用了Feistel网络,所以可以省去密钥逆向扩展模块.为了节约轮子密钥的存储空间,我们采取了在线生成轮密钥的方式.对解密操作,对于同一次ECB操作中的所有分组数据,我们只在第一组数据到来之后,正向运算出最末轮的轮密钥,并存储在额外的存储模块(Inv Key Storage)中,之后的解密操作通过在线执行密钥逆向扩展模块来在线生成.
TANGRAM的ECB模式的硬件实现在UMC 130 nm和Nangate 45 nm下进行测试,结果如表16和表17所示.其中运算周期涵盖全部32组数据所需的系统时钟数(结果由Modelsim的功能仿真所验证).我们可以看到解密比加密多花了一组加密操作的时钟周期,这是由于我们需要生成最后一轮的子密钥用于反推,但是这个操作只需要执行一次.关键路径的时长是通过Design Compiler软件分析综合网表后,通过分析时钟约束,来选取最长延迟下(maximum delay)下的关键路径所得.加解密速度根据第二轮材料说明中给出的计算方法得到.表中的面积是Design Compiler中所给出的total area的面积.经过查验对应工艺库的PDK说明文档,本设计所采用的工艺库的面积单元为平方微米.等效门GE是通过比较实现面积和该工艺下NAND2门所需面积的比值来计算,在UMC 130 nm工艺库下,NAND2所需要的面积是4 um2,而Nangate 45 nm下NAND2面积是0.798 um2.我们可以看到,不同工艺节点对整体面积的影响非常大,而等效门数基本上保持相似.
表18给出了TANGRAM的ECB模式在主流FPGA上的实现结果.通过设定时钟约束,然后综合加后端的布局布线,对于三个版本的TANGRAM的ECB模式均能满足对应时钟约束的要求.表18同时给出了在对应时钟约束下,TANGRAM的ECB模式能够达到的加解密吞吐要求.
考虑到不同应用需求,我们以128/128版本的TANGRAM为例,针对不同的应用场景进行硬件实现的优化.实际应用中,为了节省面积和高速并行化处理,计数器模式CTR被广泛采用.采用CTR模式,硬件上只需要实现加密模块,而不需要考虑解密模块,能够有效的减少硬件开销.同时CTR模式可以多个分组块并行计算,非常有利于高速处理大数据量,这一特性使得利用GPU和硬件实现来进行加速变得更加有效.因此,接下来对于不同应用场景的分析,我们聚焦于TANGRAM的CTR模式实现.
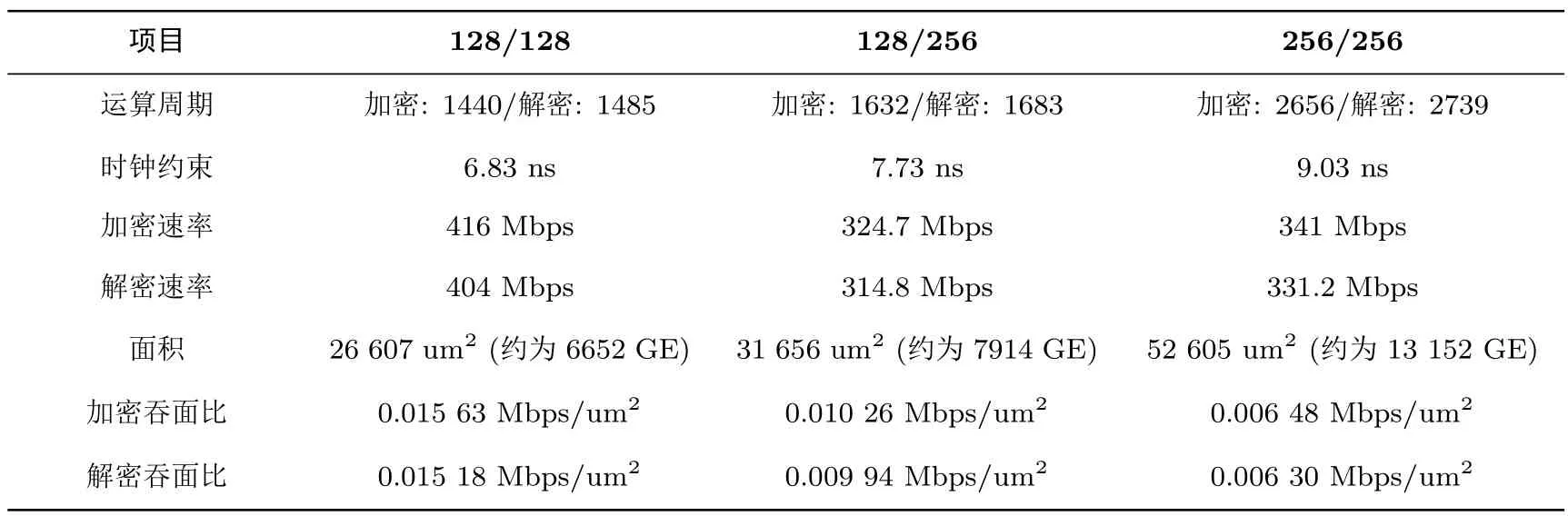
表16 TANGRAM的ECB模式在UMC 130 nm工艺库下的自测结果(全32组数据)Table 16 Results of TANGRAM in UMC 130 nm technology library(ECB mode)
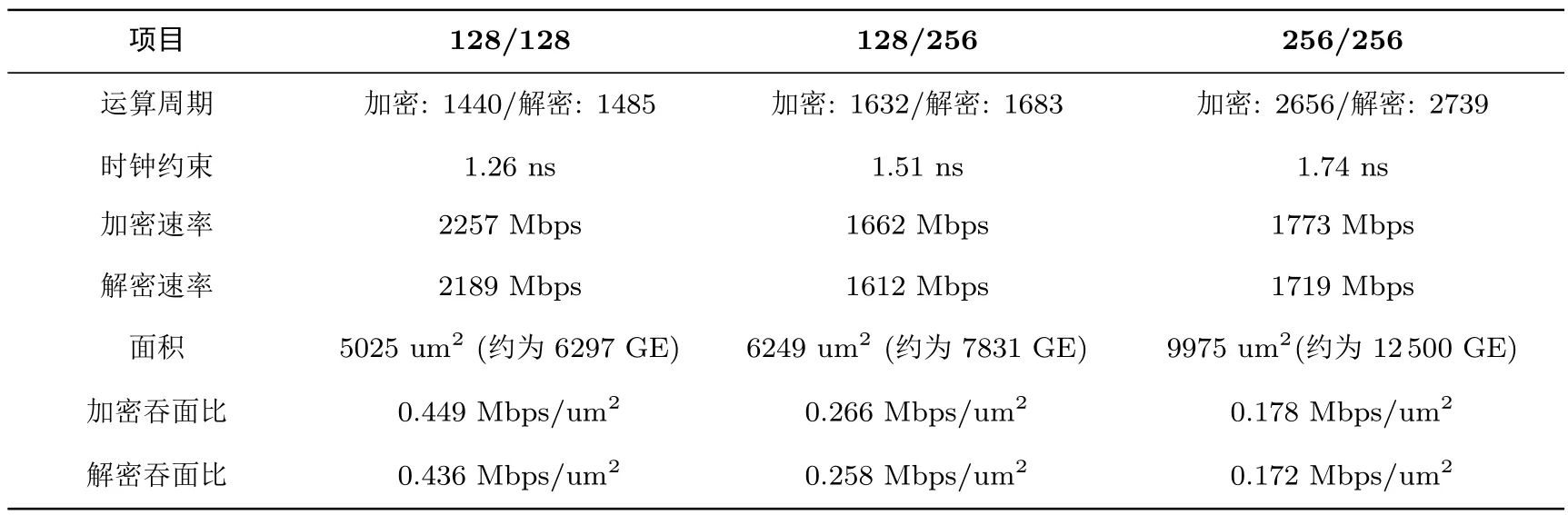
表17 TANGRAM的ECB模式在Nangate 45 nm工艺库下的自测结果(全32组数据)Table 17 Results of TANGRAM in Nangate 45 nm technology library(ECB mode)

表18 TANGRAM的ECB模式在Xilinxxc7s100fgga676-1FPGA平台下的自测结果Table 18 Results on Xilinxxc7s100fgga676-1FPGA platform in ECB mode
考虑到IoT设备的广泛使用,低面积实现往往是设计者对于轻量级应用的首要考虑因素.我们这里实现了Round-based TANGRAM.因为上述说明,我们这里采用CTR模式,仅保留其加密部分.表19中给出了Round-based TANGRAM的实现结果,并与其它模式进行了对比.我们需要强调的是,由于TANGRAM的高度灵活性,可以采用类似RECTANGLE的优化实现中串行实现的做法来进一步优化所需面积,通过高度复用AddRoundKey模块和仅仅使用1个S盒来达到面积最优的串行实现.
另一个应用场景是服务器和数据中心.这一类平台所需要处理的数据量往往非常巨大.为了满足这一类应用场景,我们给出了完全展开的全流水的版本.这一版本中,我们将所有轮的运算都实例化,并在每轮之间加入寄存器来达到流水线实现的目的.表19给出了全流水版本TANGRAM的硬件性能.这里将数据列出只是为了表明对于极端应用场景下,得益于TANGRAM算法的高灵活性,TANGRAM往往不会是包含其的加密系统中的速度瓶颈.
这里我们希望说明,高吞吐量实现和低延迟实现的需求往往并不一致.高吞吐量实现要求单位时间内能够并行处理大的数据总量.低延迟实现对数据加密开始到结束之间的延迟要求较高,典型的应用有存储器加密.一般通过完全展开轮函数,并且在每一轮之间不插入寄存器这一方法来达到低延迟实现,这种实现也被叫做单一时钟周期实现(one-clock-cycle implementation).
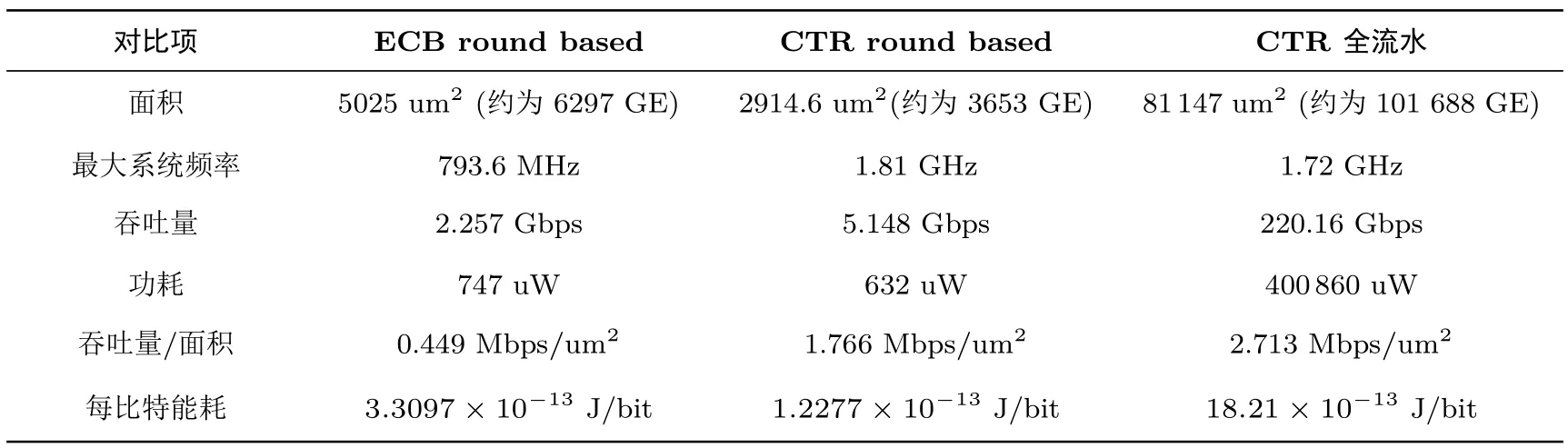
表19 多种应用场景下的TANGRAM128/128实现对比(Nangate 45 nm)Table 19 Performance of TANGRAM in multiple implementation mode(Nangate 45 nm)
根据上面多个平台多个版本的TANGRAM硬件实现结果,我们认为TANGRAM算法是一个高度灵活的、非常硬件实现友好型的分组密码.得益于其规整和统一的轮函数和密钥扩展算法,一方面针对低面积的硬件实现,可以通过高度复用相关运算模块;另一方面,针对高吞吐量和低延迟的相关应用,可以轻松实例化所有轮函数并行化来实现.
6 优点和创新点
TANGRAM的主要优点和创新点如下:
(1)设计简洁、易于扩展
TANGRAM的整体结构为SP网络,设计非常简洁:对于TANGRAM-128,128比特的加密状态用一个4×32的比特矩阵描述,S层对每一列的4个比特做S盒替换,P层对每一行的32个比特做左循环移位;对于TANGRAM-256,256比特的加密状态用一个4×64的比特矩阵描述,S层对每一列的4个比特做S盒替换,P层对每一行的64个比特做左循环移位.
TANGRAM的3个版本基于同一框架和设计方法,具有很好的可扩展性.利用这种设计思路,对于任意正整数t,可以类似地设计出分组长度为4t比特的分组密码或者固定置换,以满足不同安全需求和应用场景,比如资源有限的轻量级分组密码、认证加密方案、密码杂凑函数等.
(2)安全性分析深入
我们评估了TANGRAM抵抗差分、线性、积分、不可能差分以及相关密钥等分析方法的安全性.TANGRAM128/128的总轮数为44轮,根据评估结果,我们最多能攻击到28轮;6轮TANGRAM-128达到全扩散,因此我们在44轮的基础上又增加了6轮,将50轮作为TANGRAM128/256的总轮数;TANGRAM256/256的总轮数为82轮,我们估计最多能攻击到56轮.
我们认为:以当前分组密码分析方法的发展现状作为参考,我们为TANGRAM的3个版本预留的冗余都足够保证其抵抗数学类攻击的安全性.
(3)软件和硬件实现均表现很好
TANGRAM的主要设计思想是采用比特切片方法来设计适合多个软硬件平台的分组密码.我们在多个不同平台上实现了TANGRAM,结果表明TANGRAM的软件和硬件实现均表现很好,因此可以灵活地适用于多种应用场景.
软件实现方面:(1)在X64平台上,根据我们的测试结果,TANGRAM128/128、TANGRAM128/256、TANGRAM256/256的基本软件实现的加密速度分别是23.4、26.4和22.0 cycles/byte;在需要更为高速的应用场景,采用CTR模式,利用AVX指令集,TANGRAM128/128、TANGRAM128/256、TANGRAM256/256的加密速度可分别达到4.7、5.2和8.9 cycles/byte.(2)在32位ARM Cortex-M3平台上,可以非常方便地实现TANGRAM.根据我们的测试结果,TANGRAM128/128、TANGRAM128/256、TANGRAM256/256的加密速度分别是176.1、219.0和518.9 cycles/byte.(3)在8位AVR平台上,由我们测试结果可以看出,对TANGRAM-128,在所考虑的第一种应用情境中(采用CBC模式加解密数据且包含密钥扩展算法),在保持适中的运行时间的同时只需要极小的代码量;在所考虑的第二种应用情境中(采用CTR模式加密数据,轮子密钥直接写入程序中),只需要可忽略的随机存储内存.
硬件实现方面,我们选取了UMC 130 nm和Nangate 45 nm两个常见的工艺库来评估ASIC实现、以及Xilinx公司的7系xc7s100fgga676-1平台来评估FPGA实现.我们给出了TANGRAM三个版本在ECB模式下的硬件实现;除此之外,为了方便说明TANGRAM硬件实现的灵活性,我们同时提供了CTR模式下的纯加密模块的轻量级实现和高速实现.通过分析多个平台多个版本的TANGRAM硬件实现结果,我们认为TANGRAM是一个硬件实现友好型的分组密码,同时具有极高的灵活性和可扩展性.得益于其规整统一的轮函数和密钥扩展函数,可以通过高度复用相关运算模块来满足低面积硬件实现的需求,也可以通过实例化所有轮函数并行化来满足高吞吐量和低延迟的相关应用.设计TANGRAM的硬件实现简单便捷,仅需要较低的工程经验,非常适合快速修改整合到任意需要分组密码的系统,以提供满足针对性需求的硬件实现方案.
(4)防护侧信道代价低
得益于简洁的设计和比特切片方法,TANGRAM防护侧信道攻击的代价很低.以Threshold防护为例,TANGRAM的S盒是其中唯一复杂的部分,根据Bilgin博士等人发表于CHES 2012的论文[17],TANGRAM的S盒属于第266类,仅需要3个shares,并且在每一个share中,一阶防护仅需一对G和F函数;此外,TANGRAM基于比特切片方法设计,相比于查表实现,比特切片的软件实现能够抵抗时间缓存攻击.
(5)设计准则公开透明
TANGRAM的主要设计思想是:采用比特切片方法设计适合多个软硬件平台的分组密码.TANGRAM采用了SP网络,S层是32(或64)个4×4的S盒的并置,P层是一个比特置换.第3节我们详细给出了TANGRAM的整体设计思想和各个模块的选取准则.可以说,TANGRAM的设计,没有晦涩之处,都是基于我们对其模块的密码性质以及整体密码算法的安全性的充分理解和把握的基础之上.
(6)对模块的仔细选择
在设计TANGRAM的过程中,我们细致地挑选目标S盒,对它的两个密码指标做了特殊限制,以提升它抵抗差分/线性密码分析的性价比,详见第3.3节TANGRAM的S盒设计以及文献[18];P置换的设计也非常重要,TANGRAM的P置换仅包含3个32(或64)比特字上的循环移位,无论在硬件还是软件上都可以容易、高效地实现,这3个循环移位参数需要仔细选择,以提升算法的整体安全强度,详见第3.4节中的TANGRAM的扩散层设计;将TANGRAM的S盒和P置换组合在一起,所构成的整体密码算法具有很好的抵抗差分/线性密码分析的能力.上述因素综合在一起,TANGRAM才得以在安全性和实现性能之间达到了很好的平衡.
附录TANGRAM的比特切片实现描述
为方便描述,我们对TANGRAM-128和TANGRAM-256的密码状态进行统一的定义,在TANGRAM-128和TANGRAM-256中,这些符号分别代表不同长度的比特子块.
TANGRAM-128对于图2(b)所示的一个密码状态W,将它表示为4个32比特子块的连接,即W=A3‖A2‖A1|‖A0,其中,Ai是W的第i行,Ai=ai,31‖···‖ai,1||ai,0,i=0,1,2,3.
TANGRAM-256对于图3(b)所示的一个密码状态W,将它表示为4个64比特子块的连接,即W=A3‖A2‖A1|‖A0,其中,Ai是W的第i行,Ai=ai,63‖···‖ai,1||ai,0,i=0,1,2,3.
(1)加密轮函数
轮密钥加AddRoundKey:设轮函数的输入为I3‖I2‖I1|‖I0,轮子密钥为SK3‖SK2‖SK1|‖SK0,两者异或后的结果记为A3‖A2‖A1|‖A0,则有:
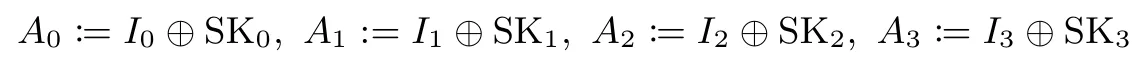
列替换SubColumn:用A3‖A2‖A1|‖A0和B3‖B2‖B1|‖B0分别表示SubColumn的输入和输出,则有:
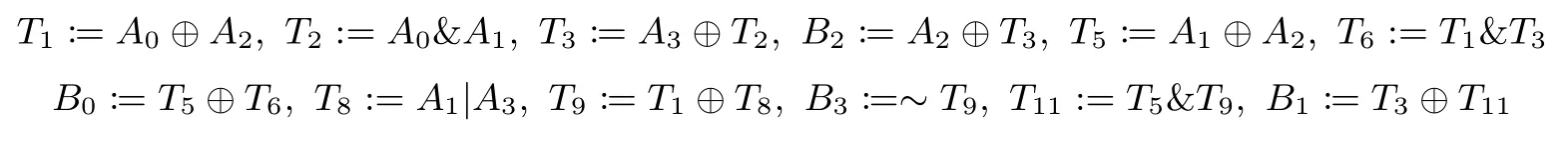
其中,“&,|,~,⊕”分别表示按位与、或、非和异或.Ti是32比特字(对应TANGRAM-128)或64比特字(对应TANGRAM-256)的临时变量,i=1,2,3,5,6,8,9,11.
行移位ShiftRow:用B3‖B2‖B1|‖B0和C3‖C2‖C1|‖C0分别表示ShiftRow的输入和输出.
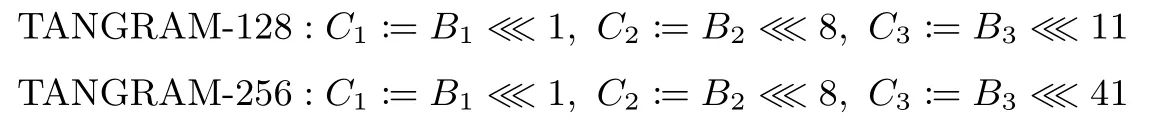
其中,A⋘x表示对32比特字(对应TANGRAM-128)或64比特字(对应TANGRAM-256)左循环移动x位.
(2)解密轮函数
轮密钥加AddRoundKey:与加密轮函数中的AddRoundKey相同.
列替换的逆变换InverseSubColumn:用B3‖B2‖B1|‖B0和A3‖A2‖A1|‖A0分别表示InverseSubColumn的输入和输出,则有:
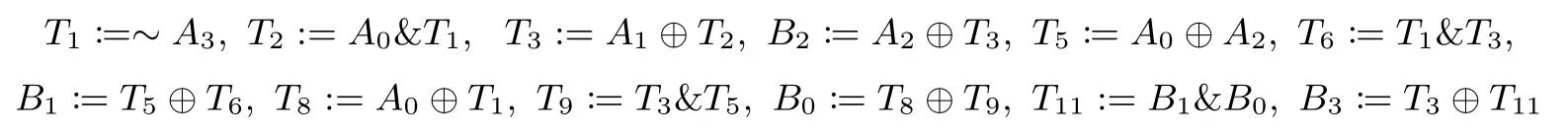
其中,Ti是32比特字(对应TANGRAM-128)或64比特字(对应TANGRAM-256)的临时变量,i=1,2,3,5,6,8,9,11.
行移位的逆变换InverseShiftRow:用C3‖C2‖C1|‖C0和B3‖B2‖B1|‖B0分别表示Inverse-ShiftRow的输入和输出.
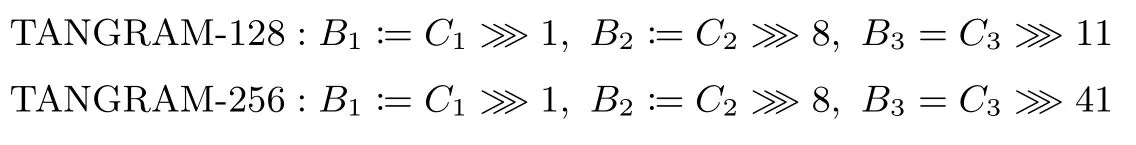
其中,A⋙x表示对32比特字(对应TANGRAM-128)或64比特字(对应TANGRAM-256)右循环移动x位.
