基于AQPSO-LSSVM的电网线损率预测模型

汪司珂　明东岳　郭雨　易本顺　项勇　潘志

摘   要：为了对地区电网220 kV线损率进行有效的评估，提出了一种基于自适应量子粒子群算法（AQPSO）优化的最小二乘支持向量机（LSSVM）的线损率预测模型。AQPSO在QPSO的基础上引入了遗传算法中的交叉与变异机制以扩大种群多样性，避免算法陷入局部最优。利用AQPSO搜索最佳的LSSVM参数并获取线损率预测结果，通过训练集对预测模型进行训练，然后使用测试集进行实验。最后选择地区电网23条220 kV线路的真实数据进行分析和预测，实验结果表明，文章所提出的AQPSO-LSSVM模型能够更有效地对线损率进行准确预测。

关键词：线损率;自适应量子粒子群;最小二乘支持向量机;220 kV电网;预测

中图分类号：TM744+.1                                       文献标识码：B

Line Loss Rate Prediction Model Based on AQPSO-LSSVM

WANG Si-ke1，MING Dong-yue1，GUO Yu2，YI Ben-shun3？覮， XIANG Yong4， PAN Zhi4

（1. Marketing Service Center，State Grid Hubei Electric Power Co.， Ltd.， Wuhan， Hubei 430077， China;

2. Electric Power Research Institute，State Grid Hubei Electric Power Co.， Ltd.， Wuhan， Hubei 430077， China;

3. Electronic Information School， Wuhan University， Wuhan， Hubei 430072，China;

4. State Grid Huangshi Power Supply Company，  Huangshi， Hubei 435099， China）

Abstract：In order to evaluate the line loss rate of 220 kV power grid effectively， a line loss rate prediction model based on adaptive quantum particle swarm optimization（AQPSO） and least square support vector machine（LSSVM） is proposed. AQPSO introduces the crossover and mutation mechanism in genetic algorithm on the basis of QPSO to expand the population diversity and avoid the algorithm from falling into the local optimum. The model uses AQPSO to search for the best LSSVM parameters and obtain line loss rate prediction results， and trains the prediction model through the training set， and then uses the test set for experiments. Finally， the article selects the real data of 23 lines of 220 kV regional power grid， for analysis and prediction， the experimental results show that the proposed AQPSO-LSSVM model can more effectively predict the line loss rate accurately.

Key words：line loss rate;AQPSO;LSSVM;220 kV grid;prediction

线损率是电力系统中一项重要的技术与经济运行指标，它能反映电网的规划、生产、管理水平[1]。电网线损率的快速准确计算对促进电力企业降低能耗、加强电网运行管理具有重要意义[2]。

传统的线损计算模型包括最大电流法、均方根电流法、平均电流法等[3～5]，但其均属于简化的电路等值模型，计算精度较低。潮流计算法是精度较高的等值模型[6]，其計算方法主要有牛顿法、PQ解耦法与回路阻抗法等。牛顿法以及PQ解耦法由于自身原理的缺点，直接应用于潮流计算中容易出现计算不收敛的问题，且计算误差较大[7];回路阻抗法主要应用于环网回路中，虽然收敛性较好，但节点与支路的编号处理复杂、计算量大且无法挖掘大量数据与配电网损耗之间的关系[8-9]。目前，规划与运行人员只能凭借经验对潮流数据进行调整，仍缺乏一套系统、有效的潮流调整方法[10]。

近年来，随着机器学习技术的迅速发展，大量的智能算法被应用于线损预测等相关领域中[11-12]，如径向基函数神经网络（Radial basis function neural network，RBFNN）[13]、长短期记忆网络（Long short term memory network，LSTM）[14]、梯度提升决策树（Gradient boosting decision tree，GBDT）[15]以及支持向量机（Support vector machine，SVM）[16]等方法。

LSSVM是SVM的改进算法之一，由于其具有较高的运行速度、计算效率与出色的非线性拟合能力[17]，已被廣泛应用于各类预测模型中，但LSSVM算法仍存在核函数参数及惩罚因子的寻优问题[18]。文献[19]利用改进后的即时学习算法优化LSSVM模型参数，提高了电力系统短期负荷预测的精度与稳定性。文献[20]采用人工蜂群（Artificial bee colony，ABC）算法优化LSSVM参数，建立了弃风电量预测模型，但ABC算法存在搜索策略过于随机、容易跳过全局最优解等问题。文献[21]利用改进的天牛须搜索算法优化LSSVM的核函数参数以及惩罚因子，对短期电力负荷进行预测，在缩短模型运行时间的同时，提高了预测的精度和稳定性。文献[22]将粒子群优化（Particle swarm optimization，PSO）的LSSVM模型应用于拉线棒腐蚀预测中，但标准PSO算法存在易早熟收敛，陷入局部最优的问题。

从分析影响线损的电气因素入手，利用改进的量子粒子群（Quantum particle swarm optimization，QPSO）算法优化LSSVM的惩罚因子与核函数参数，进而提出了一种基于自适应量子粒子群优化（Adaptive quantum particle swarm optimization，AQPSO）的LSSVM线损率预测模型。为了验证提出模型的有效性及准确性，利用湖北黄石地区23条220 kV线路的实际电力参数及历史线损数据进行验证。实验结果表明，提出的预测模型具有很好的准确性与实用性。

1   线损特征指标体系

电网线损包括输电线路的损耗、计量设备内线圈与铁芯的损耗以及电容器与电缆的介质损耗等。220 kV电网线损主要受电网布局、用电性质及用电负荷等因素的影响。考虑到电网信息的完整性还有待提高，文章选取有功功率、无功功率、均方根电流、线路长度、负载率等参数建立线损特征指标体系，从电网结构与运行负荷等方面反映电网线损特征。各线损特征指标的具体分析如下。

（1）有功功率：单位时间内，交流电路中负载消耗并转换为热能、光能、机械能或化学能等且转换过程不可逆的电量。当输送的有功功率过低时，设备功率因数会随之降低，线路损耗增加。

（2）无功功率：单位时间内，交流电路内用于建立并维持交变磁场、旋转磁场等所消耗的电量，无功功率对系统电压的稳定非常重要。无功功率过高会使总电流增加，从而增加设备和线路的损耗。

（3）均方根电流：交流电流的有效值;交流电通过某电阻时，在一周期内所产生的热量与直流电通过该电阻在同样时间内产生的热量相等，则此直流电的值即为该交流电的有效值。当输电线参数一定时，均方根电流越大，损耗越大。

（4）线路长度：导线本身存在电阻，其阻值与线路长度成正比。线路越长，阻值越大，从而线损也越大。

（5）负载率：线路出现的最大负荷与线路本身最大载容量之比。反映了线路的负荷水平，值越大，线路的利用率越高。

2   基于AQPSO优化的LSSVM预测模型

提出了一种基于AQPSO优化的LSSVM模型对220 kV电网线损率进行预测，下面将对其原理进行详细介绍。

2.1   LSSVM回归模型

SVM基于结构风险最小化，能较好地解决机器学习中存在的局部极小值、过学习、维数灾难、非线性等问题，具有较好的泛化能力[23]。但是面对大规模样本时，就会暴露其稳定性差、训练速度慢等缺点。针对这一问题，Suykens等人在此基础上提出了LSSVM[24]，降低了算法的复杂度，提高了训练速度，更适用于大样本序列的拟合预测。LSSVM将SVM优化问题的非等式约束用等式约束替换，且把经验风险由偏差的一次方改为二次方，其基本原理如下。

设训练数据集为T = {（xi，yi） | i = 1，2，…，l}，其中xi∈Rn，为n维向量，yi为输出，l则为训练样本个数。利用非线性函数φ将样本映射至更高维的空间，再进行线性回归，相应的表达式为：

f（x） = wT φ（x） + b        （1）

其中，w为权重向量，φ（x）为x的映射函数，b为偏置常数，相应的优化目标函数为：

min J（w，ξ） = ■wT w + ■C■ξ 2i        （2）

对应的约束条件为：

yi = wφ（x） + b + ξi，i = 1，2，…，l        （3）

式中，C为惩罚参数，ξi为误差变量。引入的拉格朗日函数为：

L（w，b，ξ，α）=J（w，ξ）-■αi（wT φ（xi）+b+ξi -yi）

（4）

其中，αi为拉格朗日乘子，且αi≥0，将上式代入KKT（Karush-Kuhn-Tucker）条件可得：

■ = 0 ？圯 ■αi φ（xi） = 0■ = 0 ？圯 ■αi = 0■ = 0 ？圯 αi = Cξi，i = 1，2，…，l■=0？圯wT φ（xi）+b+ei -yi =0，i = 1，2，…，l（5）

对上式进行求解，根据Mercer条件[25]确定的核函数为：

K（xi，xj） = φ（xi）T φ（xj）            （6）

相应的LSSVM模型的预测表达式为：

f（x） = ■αi K（x，xi） + b         （7）

2.2   AQPSO算法

LSSVM模型中的惩罚参数、适应度函数，以及核函数中宽度系数的选择，往往带有一定的主观性，会对预测造成显著的影响，无法保证算法的精度[26]。为了解决此问题，本节将引用能对参数进行优化的自适应量子粒子群算法，从而找到LSSVM预测模型最合适的参数。

2.2.1   QPSO算法

2004年，Sun等人受到量子力学的启发，在此基础上提出了QPSO算法[27]。在量子力学中，根据不确定原则可知，粒子的速度与位置是无法同时确定的，且粒子的运动没有确定的轨道。与PSO相比，QPSO没有速度的概念，减少了需要调节的参数，且能在优化问题上表现得更好。

QPSO算法中，设一个群体为S（X1，X2，…，XN），其中的Xi为粒子，粒子数目为N，每个粒子的位置为Xi = （Xi1，Xi2，…，Xid），维度为d。Pbesti为第i个粒子的最优解，用Pi = （Pi1，Pi2，…，Pid）表示，Gbest则为整个群体找到的最优解，用Pg = （Pg1，Pg2，…，Pgd）表示。用波函数ψ（x，t）描述粒子的状态，再通过薛定谔方程对其求解，得到粒子出现在空间某一点的概率密度函数。随后采用蒙特卡洛方法，得到粒子位置的更新方程如下：

X（t + 1） = P（t） ± ■ln（1/u）        （8）

P（t） = φPi（t） + （1 - φ）Pg（t）     （9）

在上式中，u和φ为在[0，1]的独立随机数，Pi（t）为第i个粒子在t次迭代中个体的最佳位置，Pg（t）为t次迭代中群体的最佳位置。L的定义为：

L（t + 1） = 2 βmbest - X（t）        （10）

mbest = ■Pi /N =

■Pi1 /N，■Pi2 /N，…，■Pid /N   （11）

其中，β是收縮扩张系数，用于调节算法的收敛速度。一般最初被设为1，采用线性减小的控制策略。但是此算法容易陷入局部最优解，文章在此基础上进行改进，提出了AQPSO算法。

2.2.2   AQPSO算法

检测群体有效性的一个重要指标为群体多样性，多样性降低的过程代表向最优值收敛与查找可寻空间的平衡。文章采用的多样性度量方法如下：

Diversity（S（t））=■■■

（12）

■ = ■         （13）

其中，S为整个群体，L为搜索空间的最长对角线的长度，Xj是每个粒子第j个维度的平均值。

AQPSO算法以群体进化过程中的多样性程度，自适应地进行了调整，兼顾群体收敛速度与种群多样性。在进化的前中期，多样性的降低有利于更快地向最优解靠拢;但在中后期，多样性过低可能会导致粒子集中聚集在一个区域内，陷入了局部最优。针对这一问题，在QPSO的基础上引入了遗传算法中的交叉与变异机制以扩大种群多样性，避免算法陷入局部最优。

当群体在进化过程中的多样性大于或等于阈值dlow时，将选取适应度最差的粒子，将其对应的Pbestworst与另一个随机选择粒子的Pbestrand交叉产生两个新的个体：

X1    new = r × Pbestworst + （1 - r） × Pbestrand     （14）

X2    new = （1 - r） × Pbestworst + r × Pbestrand     （15）

其中，r为（0，1）之间的随机数，分别计算新粒子X1    new与X2    new的适应度，比较得到适应度较好的粒子。再将选择的新粒子与原粒子中适应度最差的粒子进行比较，若新粒子适应度更好，则用新粒子替换原有粒子;若原粒子适应度更好，则维持原状。这样能使粒子群更快地向最优解靠拢，缩短迭代时间。

当多样性小于阈值时，采取变异策略，尽量避免其陷入局部最优值点。变异时，随机选择一个粒子，对其进行下列操作：

Xi j（t）=Xi j（t）+（Xi j（t）-XMAXj）× f（t）   r≥0.5 Xi j（t）+（XMINj -Xi j（t））× f（t）    r<0.5

（16）

f（t） = r × （1 - t / Maxiter）2        （17）

其中，XMAXj和XMINj分别为粒子每个维度的上边界和下边界，t为当前迭代次数，Maxiter为迭代的最大次数。用新生成的粒子取代被选中的粒子，适应度也进行相应的替换。

2.3   AQPSO-LSSVM模型

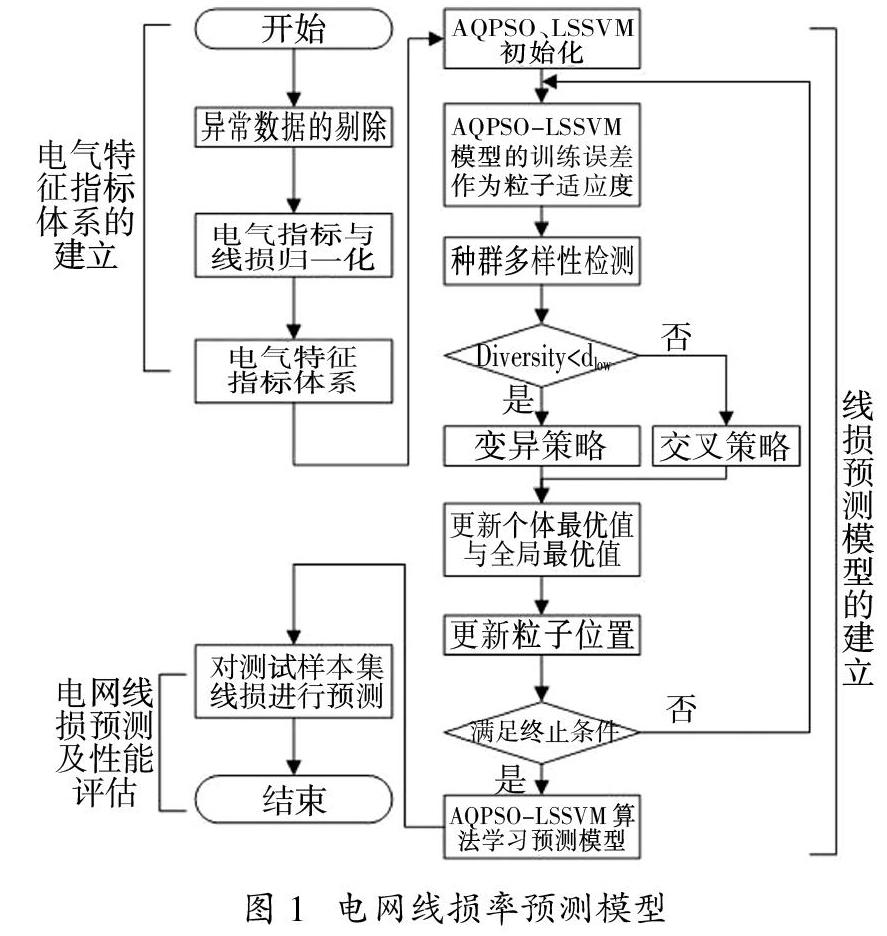
基于AQPSO优化的LSSVM电网线损率预测模型的流程图如图1所示，主要分为三部分，即电气特征指标体系的建立、线损率预测模型的建立和线损率预测和模型评估。具体实现步骤如下：

（1）建立电气特征指标体系。对各指标（有功功率、无功功率、均方根电流、线路长度、负载率）进行归一化处理并剔除异常数据。构造电气特征指标体系，划分样本集和测试集。归一化处理公式如式（18）所示。

Xnorm = ■       （18）

式中，Xnorm为归一化后的数据，X为原始数据， Xmax、Xmin为原始数据集中的最大值与最小值。

（2）以五个指标作为输入，预测统计线损率作为输出，放入模型进行训练。在训练过程中，计算此时种群的多样性，若小于阈值，实行变异策略;若大于阈值，实行交叉策略。

（3）随后更新全体最优值、局部最优值及粒子位置。再判断此时是否满足迭代终止的条件，若满足，则确定了AQPSO-LSSVM线损率预测模型;若不满足，重复步骤（2）与步骤（3），直至满足迭代终止的条件。

（4）220 kV电网线损率的预测及模型性能评估。用训练好的模型对测试集的数据进行测试，获得预估线损率，并用MAE、RMSE、MRE指标进行性能评估。

2.4   模型评估

使用上述模型进行预测后，使用平均绝对误差（MAE）、均方根误差（RMSE）、最大相对误差（MRE）对预测结果进行性能评估，三种误差分析指标算法如下：

MAE = ■■Yi - ■i×100%     （19）

RMSE = ■    （20）

MRE = Max■×100%    （21）

其中，Yi为真实值，■i为预测值。

3   实验结果与分析

为了验证上述方法的有效性，以湖北黄石电网的真实数据为例，选取了该地区电网23条220kV 线路在2019年10月份的数据。每天为一组样本，每组样本的输入指标为有功功率、无功功率、均方根电流、线路长度、负载率;输出指标为统计线损率。在剔除异常数据后，共580组数据，其中训练样本集数量为516，测试集数量为64。实验仿真的计算机主要硬件配置如下：CPU为Intel？誖CoreTM i7-6850K，基准频率3.60 GHz;GPU为NVIDIA GeForce GTX 1080 Ti，内含11 GB显存。

利用516組样本构成的训练数据集，按照2.3节所述的流程对AQPSO-LSSVM模型进行训练。设定的种群粒子数N为30，收缩扩张系数β初始值为1，采用线性减小的控制策略。随后根据群体多样性 的值，再选择变异策略或交叉策略，迭代次数为500。

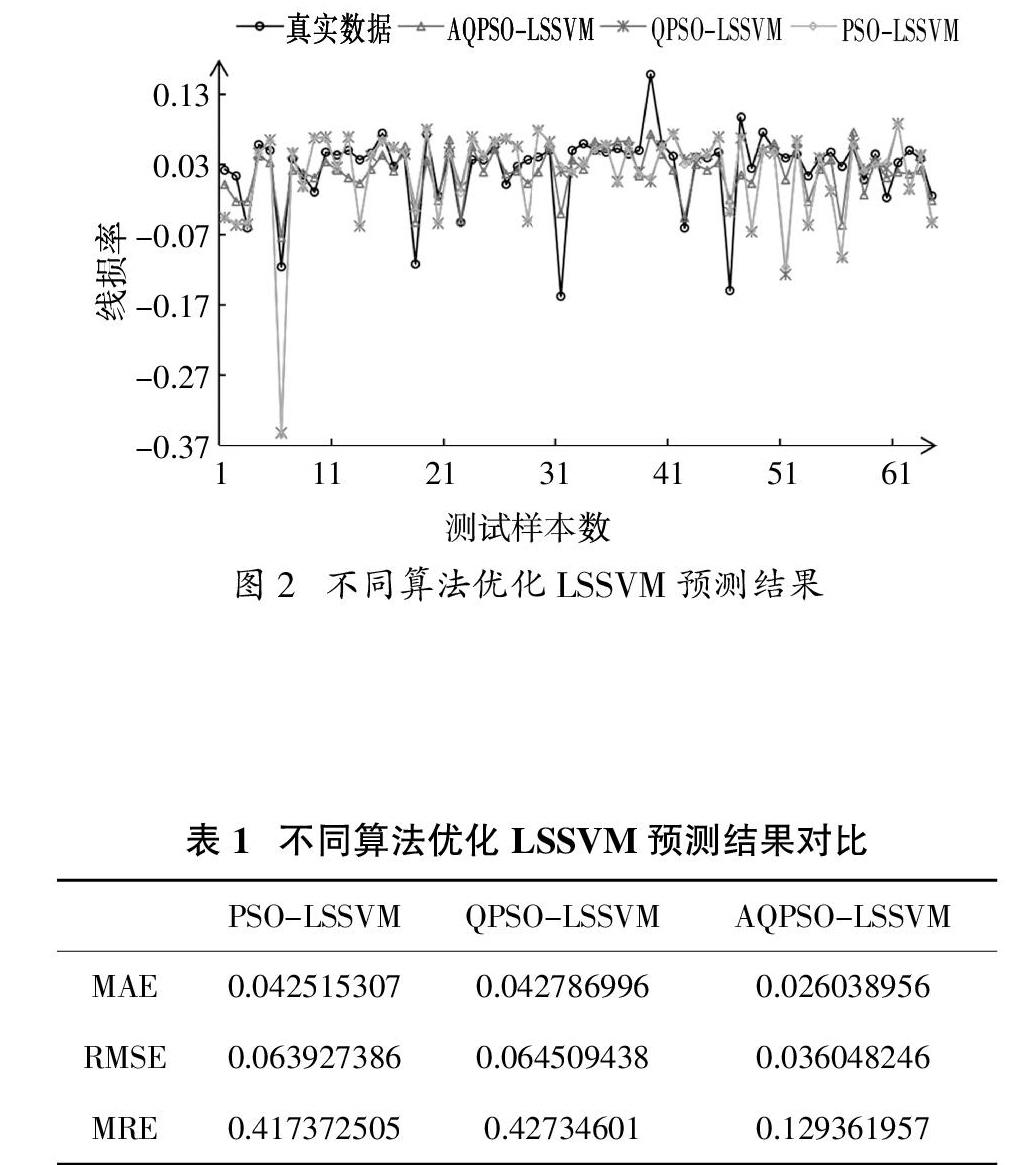
首先比较了PSO-LSSVM、QPSO-LSSVM、AQPSO-LSSVM三个模型的效果，预测结果如图2所示，AQPSO-LSSVM模型的预测结果与真实数据最为贴合，在大部分转折处预测较准确，均方根误差仅为0.036;而PSO-LSSVM与QPSO-LSSVM模型的预测结果几乎一致，与原始数据相差较大，其均方误差分别为0.064，0.065。

由表1可知，PSO-LSSVM与QPSO-LSSVM的MAE指标分别为4.25%，4.28%，即QPSO-LSSVM对PSO-LSSVM的性能基本没有改进，预测容易陷入局部最优;而AQPSO-LSSVM则有很明显的改进，其MAE，RMSE，MRE分别为2.6%、0.0013，12.9%，说明引入的遗传机制发挥了作用，能让预测结果更为准确。

4   结   论

线损率的准确预测对于电力相关部门乃至整个社会用电消费都有及其重要的作用。传统的LSSVM模型虽然能预测线损率，却容易陷入局部最优的情况;PSO-LSSVM模型能在一定程度上优化参数，却增加了参数数量;QPSO-LSSVM在PSO-LSSVM的基础上减少了参数，却容易出现早熟收敛的情况。为了对电网线损率进行有效的评估，提出了AQPSO-LSSVM模型，既减少了相对于PSO-LSSVM所需要的参数量，也克服了QPSO-LSSVM易陷入局部最优的缺陷。AQPSO-LSSVM在QPSO-LSSVM的基础上，引入了遗传机制，在可能陷入局部最优的情况时采取交叉或变异的方法，从而跳出局部最优，向全局最优靠近。最后，以湖北黄石电网220 kV线路的真实数据为例，验证了该模型的准确性及实用性。

参考文献

[1]    吴鸿亮，门锟，董楠，等. 基于J2EE架构的线损理论计算与诊断分析系统开发与应用[J]. 电力系统保护与控制，2016，44（05）：108-116.

[2]    丁忠安，高琛，蒋敏敏，等. 基于专家样本库和最小二乘支持向量机的配电网线损率预测模型[J]. 水电能源科学，2020，38（03）：195-198.

[3]    吉杨，郑华，段云琦，等. 基于积分电流法的配电网理论线损计算[J]. 东北电力技术，2017，38（9）：39-43.

[4]    曾江，李石东. 分时域10kV配电网极限线损计算分析[J]. 电测与仪表，2019，56（14）：1-4，22.

[5]    JING T T，LI D，XI H J，et al. Method for Theoretical Line Loss Calculation of 10kV Distribution District based on Actual Electric Energy of Distribution Transformer Secondary Side[C]//IOP Conference Series：Earth and Environmental Science. IOP Publishing，2019，218（1）：1-8.

[6]    邓红雷，张莉彬，唐崇旺，等. 一种含分布式电源的配电网三相潮流混合计算方法[J]. 电力系统保护与控制，2020，（14）：10-17.

[7]    张捷，徐焰，张学飞. 一种改进前推回代法的配电网潮流计算[J]. 四川电力技术，2020，43（3）：85-90.

[8]    夏翔，董大伟，方建亮，等. 基于PCA-ELM的日同期线损检测系统的研发[J]. 电子测量技术，2018，41（7）：99-104.

[9]    李云冰，徐兰兰，王晓军，等. 基于门控循环神经网络的线损电量预测方法[J]. 电力设备管理，2020，（2）：132-134.

[10]  安军，宋俊达，葛维春. 大规模电力系统潮流计算收敛性诊断与调整方法[J]. 电力自动化设备，2020，40（2）：103-109.

[11]  ZHENG De-hua，ABINET T E，ZHANG Jian-hua，et al. Short-term wind power forecasting using a double-stage hierarchical ANFIS approach for energy management in microgrids[J]. Protection and Control of Modern Power Systems，2017，2（2）：136-145.

[12]  WU W，CHENG L，ZHOU Y，et al. Benchmarking daily line loss rates of low voltage transformer regions in power grid based on robust neural network[J]. Applied Sciences，2019，9（24）：5565-5582.

[13]  姜全坤，李英娜，李川. 改进PSO优化RBF网络的电网线损计算方法[J]. 信息技术，2019，43（05）：61-64.

[14]  JIA H，DENG Y，QIU X，et al. Line loss rate prediction method based on deep learning with long short term memory[C]//2019 14th IEEE Conference on Industrial Electronics and Applications （ICIEA）. IEEE，2019：392-396.

[15]  YAO M，ZHU Y，LI J，et al. Research on predicting line loss rate in low voltage distribution network based on gradient boosting decision tree[J]. Energies，2019，12（13）：2522-2536.

[16]  陈勇，李鹏，张忠军，等. 基于PCA-GA-LSSVM的输电线路覆冰负荷在线预测模型[J].电力系统保护与控制，2019，47（10）：110-119.

[17]  段铭. 基于改进LSSVM的火电企业低碳发展水平评价研究[D]. 北京：华北电力大学，2019.

[18]  赵允，何立强，于景亮.基于灰色关联分析和IPSO-LSSVM的线损预测模型研究[J]. 东北电力技术，2020，41（04）：6-10.

[19]  朱清智，董澤，马宁. 基于即时学习算法的短期负荷预测方法[J]. 电力系统保护与控制，2020，48（7）：92-98.

[20]  谢丽蓉，杨欢，轩武警，等. 基于ABC-LSSVM的弃风电量预测[J]. 水力发电，2019，45（12）：101-104.

[21]  闫重熙，陈皓. 基于改进天牛须搜索算法优化LSSVM短期电力负荷预测方法研究[J]. 电测与仪表，2020，57（6）：6-11，18.

[22]  孟遂民，向乃瑞，黄力. 基于PSO-LSSVM的拉线棒腐蚀预测[J]. 腐蚀与防护，2020，41（1）：23-28.

[23]  谢荣燕，赵明. 基于支持向量机的企业生产设备采购预测模型研究[J]. 计算技术与自动化，2018，37（4）：139-142.

[24]  SUYKENS J A K，VANDEWALLEJ，DE MOOR B. Optimal control by least squares support vector machines[J]. Neural Networks，2001，14（1）：23-35.

[25]  NAIK J，DASH P K，DHAR S. A multi-objective wind speed and wind power prediction interval forecasting using variational modes decomposition based Multi-kernel robust ridge regression[J]. Renewable Energy，2019，136：701-731.

[26]  LIU Y，WEI T，ZHANG W，et al. Short-term daily load forecasting in distribution power system based on VMD & BA-LSSVM combined method[C]//2019 IEEE Innovative Smart Grid Technologies-Asia （ISGT Asia）. IEEE，2019：364-368.

[27]  SUN J，XU W B. A global search strategy of quantum-behaved particle swarm optimization[C]// Proceedings of the IEEE Congress on Cybernetics and Intelligent System. Singapore：IEEE Press，2004：111-116.