工程参数扰动性计算方法的选择与分析

于 洋，职保平，2，秦净净

(1.黄河水利职业技术学院，河南开封475000；2.西藏自治区水利电力规划勘测设计研究院，西藏拉萨850000)

工程中存在物理不确定性、统计不确定性和模型不确定性三大类，其中物理不确定性主要包含材料常数、几何尺寸、荷载及边界条件等；统计不确定性主要指工程中的误差、扰动常采用统计方法进行分析，但噪声等因素的存在，必然使统计结果存在误差；而模型不确定性是指简化所得的数学模型与实际结构之间差异所以引起的模型计算响应和实际结构响应的偏差[1]。

在水利工程中，特别是西藏水利工程中，由于环境特性导致多个各参数的误差进一步放大。这些误差是客观存在的，已有研究表明，结构参数的扰动性可能引起结构动力特性和动力响应的大幅度变化，使力学参数的扰动性在一定条件下成为主导因素[2]。文献[3]表明，结构最大响应的变异系数通常是结构参数变异系数的2～4倍，即扰动性引起误差的幅值为确定参数解的2～4倍，还有文献给出的算例高达7倍；与此同时，结构参数的随机性对动力响应的贡献量一般大于外激励贡献量[4]。显而易见，按照确定参数分析得到的结果，并不能完全精确地描述结构的真实动态行为。目前针对结构参数扰动性问题，在计算时一般使用概率模型、模糊模型、区间模型[5- 6]三类模型进行处理，但参数扰动的研究在水利工程行业中并不深入，成果较少，多是单参数的计算分析，而采用随机参数结构方法的研究十分匮乏。

本文团队分别将概率摄动法[7]、二阶摄动法、LR模糊数[8]以及区间参数[9-10]方法引入水电机组振动传导问题中，推导了相关的计算过程，但最终各方法的计算特性未开展横向对比研究，本文以水电机组振动传导为例，分别采用概率模型中的摄动法、LR模糊数法、区间参数法进行横向计算对比研究，分析在考虑结构参数存在扰动时，各方法的计算性能，最终为水利工程计算参数扰动问题提供方法选择依据。

1 随机摄动法

应用概率模型中摄动法时，要求各参数扰动量小范围变化，一般小于15%，同时需要已知参数的概率特性，一般假定为正态分布，利用其线性变换也服从正态分布这一特性进行计算，应用随机摄动理论，随机变量分解为确定部分和扰动部分

(1)

式中，ε为小参数；上标d表示确定部分，在实际应用中表示多次采样后的均值；上标p表示扰动部分，实际应用中具有零均值性质，同时要求随机部分比确定部分小得多。

对式(1)求数学期望

(2)

式中，Ea为21×1阶，EFt为1×1阶。同样，求方差，根据Kronecker代数及其相应的随机分析理论得[11-12]

(3)

根据Taylor展式，将Ft在Ftd处一阶展开得

(4)

将式(4)带入式(1)得

(5)

从而得到传递力的扰动范围。

2 LR模糊数法

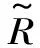
(6)

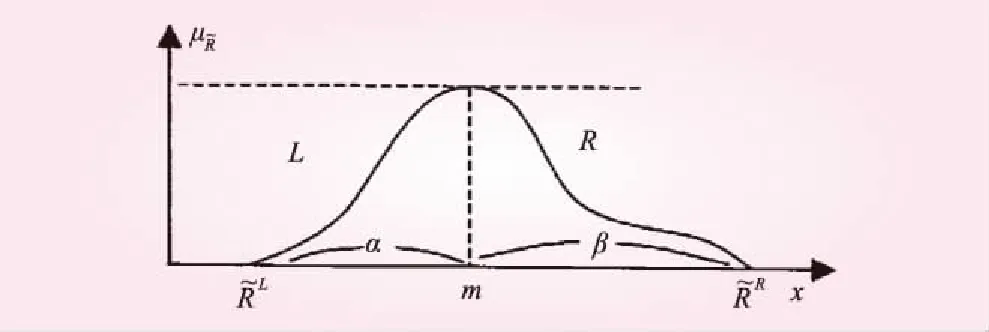
图1 LR型模糊数

(7)

(8)

图2 LR三角型模糊数

(9)

(10)

根据模糊数运算法则得

(11)

(12)

3 算例分析

以混流式水电机组振动传导分析为例，其振动简化模型见图3，各方法采用统一模型计算。由于本文是探讨各方法是计算性能，模型简化过程不作为主要问题进行阐述，详细简化过程见文献[7]，不考虑蜗壳及其下部结构影响，假设激励为单频简谐激励，各参数均值由水电站施工设计图及生产厂商提供资料计算及折算得到，其中采用比例阻尼进行分析，各参数均值如下m1=8.28×104，m2=1.042×106，m3=3.29×105，m4=9×105，m5=1.2×105，m6=1.39×105，m7=8.92×105，m8=1.15×105质量m的单位为kg；k1=7.26×1010，k3=5.72×1010，k4=2.32×1010，k51=2.20×1012，k52=9.41×109，k6=7.70×109，k7=4.26×108，k81=1.73×108，k82=1.73×1010，刚度k单位N/m；c1=5.48×106，c3=4.11×106，c4=1.02×107，c51=2.56×107，c52=7.51×104，c6=1.64×106，c7=9.74×105，c81=2.23×105，c82=9.99×104，阻尼c的单位为N·s/m。

图3 伞式机组竖向振动简化模型

这些参数中，油膜、水封的刚度参数非线性强，且难以测量，参数具有很强的不确定性，由此取k51，k81，c51，c81区间半径为0.1倍的均值；顶盖上承载的控制部件等附加部件较多且重量、刚度、阻尼的计算采用折减系数得到，因此存在不少不确定，取k82，c82区间半径为均值的0.05，取机墩等质量单元的区间半径为均值的0.001。

采用各方法计算传递率的结果如图4～图7所示，传递率为传递力与激振力的比值，能够更为明确的表述各方法计算的特性。在计算中，采用摄动

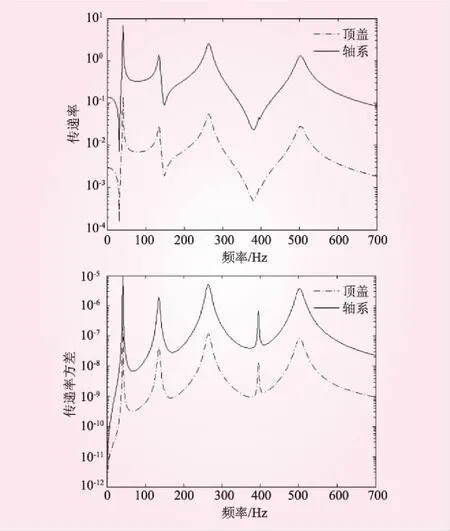
图4 摄动法计算传递率及传递率方差特性曲线

图5 LR模糊数法计算不同截集水平下的传递率分布图及局部放大示意

法计算时，由方差转化为均值倍数关系为均值的1.7841%～12.2%；采用LR模糊数计算方法，采用三角形模糊函数时，最大边界范围为均值的-26.2%～26%；采用区间参数计算时，最大边界范围为均值的1.06%～14.11%。

图6 各截集下不同固有频率处的路径传递率模糊度

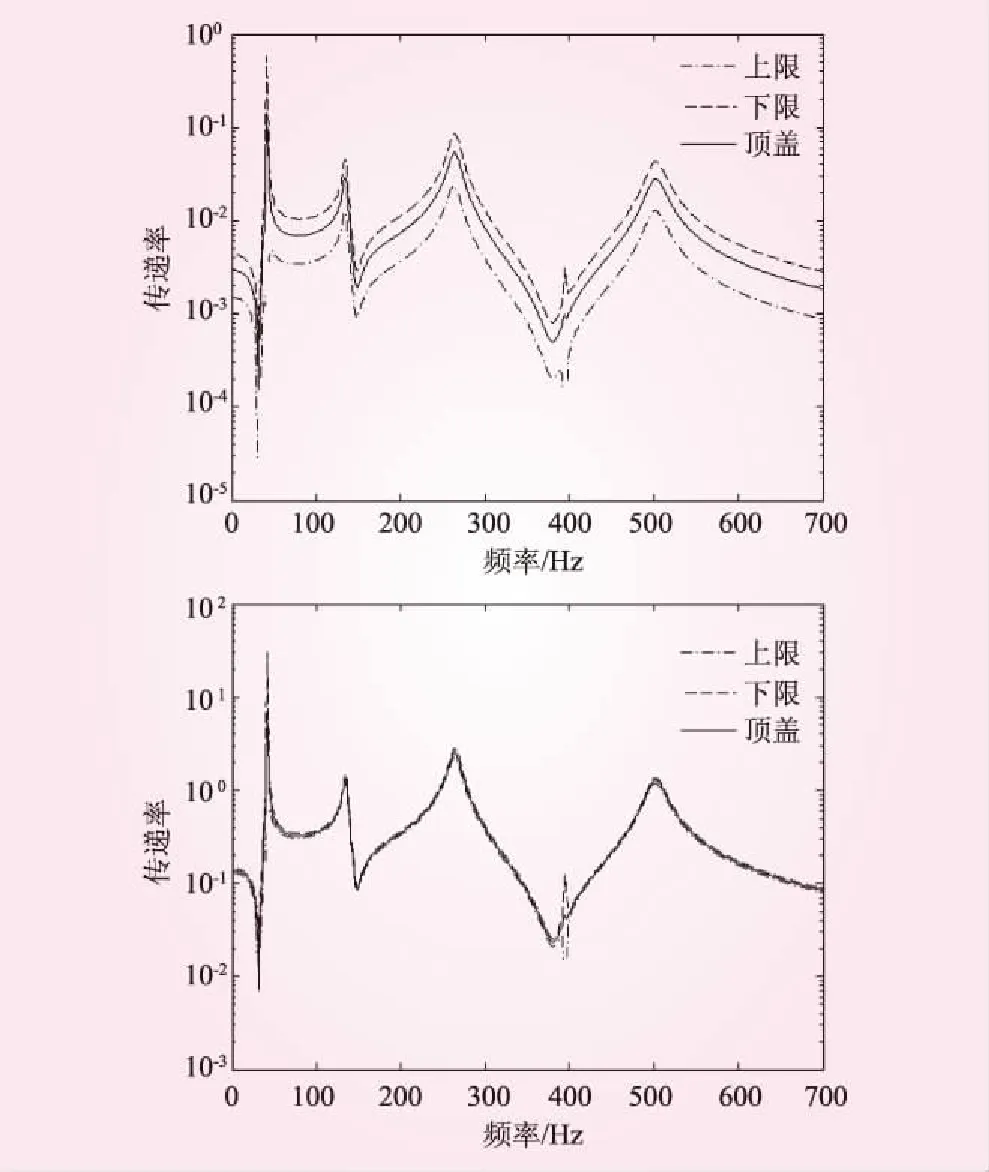
图7 区间参数计算各路径传递率及取值上下限

4 结 论

本文参数扰动分析中，分别采用随机摄动法、LR模糊数法、区间参数方法来描述分析中所遇到参数不确定问题，结果显示：

(1)三类方法在计算过程中均表现出相同的变化趋势，顶盖路径与轴系统路径的比例分配大致相同，均在固有频率处出现极值，三类方法在计算水电机组振动传导问题时均可以得到有效解。

(2)从各方法的计算结果来看，区间参数方法计算得到的扰动范围下限最小，上限较摄动法略有增加，其结果质量与随机摄动法不相上下，而LR模糊数法则扰动范围发生扩张，当结构参数进一步增加，参数扰动区间扩大时，其结果将产生更为不利扰动区间扩张。

(3)三类方法中，随机摄动法、LR模糊数法需要一定的已知或假设条件，因此在计算水电机组振动传导问题时，建议采用区间参数方法。

本文针对水电机组振动传导问题展开参数扰动性的方法计算分析，但所采用的三种方法并不限定于水电机组，其方法同样适用于水利、土木等土建结构，方法性能的选择为分析确定结构随机问题提供了思路以及理论支撑。