一种非球面反射镜有效通光口径的定量化检测方法
2020-01-03孟晓辉张继友王永刚李昂周于鸣李文卿
孟晓辉 张继友 王永刚李昂周于鸣李文卿
一种非球面反射镜有效通光口径的定量化检测方法
孟晓辉1,2张继友1,2*王永刚1,2李昂1,2周于鸣1,2李文卿1,2
(1 北京空间机电研究所,北京 100094)(2 国防科技工业光学超精密加工技术创新中心(先进制造类),北京 100094)
有效通光口径是非球面反射镜的一项重要指标参数,但在现有检测工艺中存在着难以定量化检测、测试误差大等问题,导致在后续系统复算过程中难以对成像品质进行正确评估。为了解决这些问题,文章提出在干涉检测阶段采用非线性误差校正的方法来对非球面反射镜的有效通光口径进行检测。首先是通过光线追迹的方法采集一系列干涉仪CCD坐标系和待测反射镜坐标系下的坐标点数据;然后对坐标点数据进行多项式函数拟合,建立两者间非线性误差函数关系;最后以干涉仪CCD坐标系尺度下的有效干涉条纹图形作为输入,反算出镜面尺度下反射镜的实际有效通光口径。在工程应用实例中,对某型号空间相机中的一块米级非球面反射镜进行了实际检测,单边测试精度为干涉仪1个像素所对应的镜面尺度误差,且该方法的测试误差主要取决于测试系统中所选用干涉仪CCD平均分辨率的大小;分别将校正前后的反射镜参数代入到系统中进行复算,光学系统调制传递函数MTF值的偏差达到了0.013@71.5线对/mm。结果表明,应用该方法不仅可以在加工过程中对反射镜的有效通光口径进行实时监测,还能正确评估相机地面装调阶段的光学系统成像品质,在空间光学元件先进制造领域具有重要的工程应用意义。
光学加工 光学检测 非球面反射镜 有效通光口径 非线性误差校正 空间光学相机
0 引言
随着空间卫星光学遥感技术的发展,天基大口径反射镜的制造呈现了两极化发展,从宏观尺度上,在大型高分辨率空间光学载荷系统设计中,为了实现更高分辨率的观测,反射镜的口径从米级向十米量级迈进[1-2]。从微观尺度上,对空间光学元件的加工品质有了更加精细的要求,一方面为了提高系统的成像性能,要求反射镜的面形精度、光学参数及几何参数等指标都要达到现有加工能力的极限;另一方面从工程实现角度,光学设计加工装调一体化的研制需求成为后续遥感相机的主流研制思路。所以非球面反射镜的加工已经不再像传统制造工艺那样仅仅关注镜面指标,而是与光学设计、光学装调和光学检测形成闭环的反馈,以满足对相机成像品质日益精益化控制的要求[3]。
有效通光口径是非球面反射镜在光学加工过程中的一项重要光学参数。在卫星光学载荷研制过程中,首先在反射镜加工阶段获取准确的数值输入,提供给光学设计,然后在成像系统中进行仿真复算来计算出光学系统调制传递函数(MTF),从而在地面光学装调阶段预先对相机的成像性能进行正确评估[4-6]。但在实际的光学加工检测过程中,对有效通光口径这一指标的关注度不够,其测量仍然是采用传统工艺中的“标记法”来进行检测。对于米级以上的大口径非球面反射镜,边缘误差多为塌边,陡度大[7-9],在进行干涉仪检测时,边缘条纹较为密集,应用这一方法难以分辨出实际的镜面边缘。另外在镜面上粘贴标记点时,由于干涉检测中补偿元件的引入,镜面标记点坐标与干涉图上的坐标不再是一一线性对应关系,呈现非线性误差,这也带来测量误差。文献[10-13]对非线性误差的产生进行了详细的描述和分析;文献[14-15]结合离轴非球面反射镜的加工实例,完成了离轴非球面反射镜在计算全息检测系统中的面形畸变校正,并取得了较好的收敛效率。上述研究成果侧重于解决检测坐标和加工机床坐标两种不同坐标系下的面形畸变复原难题,并未对反射镜的几何参数指标演变规律进行进一步的分析。另外,由于非球面通光口径的测试误差,在进行面形畸变复原时,也会产生新的误差。在光学镜头成像领域,也有针对于非线性畸变误差校正的研究[16-17],虽然所属领域不同,但在数据拟合算法等方面仍具有一定的借鉴意义。
本文提出应用非线性误差校正的技术方法来对大口径非球面反射镜的有效通光口径进行定量化检测。结合某型号大型空间光学遥感器中一块米级非球面反射镜的加工检测实例,通过光线追迹的方法获取一系列干涉仪CCD坐标系和待测反射镜镜面坐标系下的离散点坐标数据,并通过数学计算的方法,建立两者间的非线性误差畸变关系;然后在实际测试中,对干涉仪的CCD平均分辨率进行标定,计算出CCD坐标尺度下的通光口径;最后根据非线性误差曲线,换算出待测反射镜的实际有效通光口径。
1 非线性误差的产生
在对平面反射镜进行测试时,由于可以采取干涉仪直接对其面形进行测试,所以干涉仪内CCD坐标系与镜面坐标间是一一对应、不存在任何误差关系。但对于非球面反射镜,一般需要引入额外的补偿光学元件,如零位补偿器或计算全息片(CGH),来构成检测光路[18-19](如图1所示),根据补偿元件和反射镜参数选择合适的标准参考镜镜头即可实现对非球面反射镜的测试。

图1 非球面反射镜检测光路
但在进行非球面反射镜面形测试时,由于零位补偿器以及激光干涉仪在准直、CCD成像过程中引入的误差,会导致干涉检验的CCD测量坐标系与反射镜镜面坐标系之间的对应关系不再是一一线性对应关系,镜面坐标在CCD测量坐标系下的投影呈现一种非线性畸变。以圆形通光口径为例,在入瞳平面上等径向间隔离散采样,绘制出这些点阵经过补偿系统后在待测镜面上的投影坐标(镜面任意两条正交轴线,取方向的坐标值),见图2。非线性畸变前,即模拟的理想投影坐标,经过补偿光学系统后产生了非线性畸变误差,坐标明显偏离,这一偏离量,不能通过简单的线性函数关系来表征,需要通过数据拟合的方法来进一步描述。
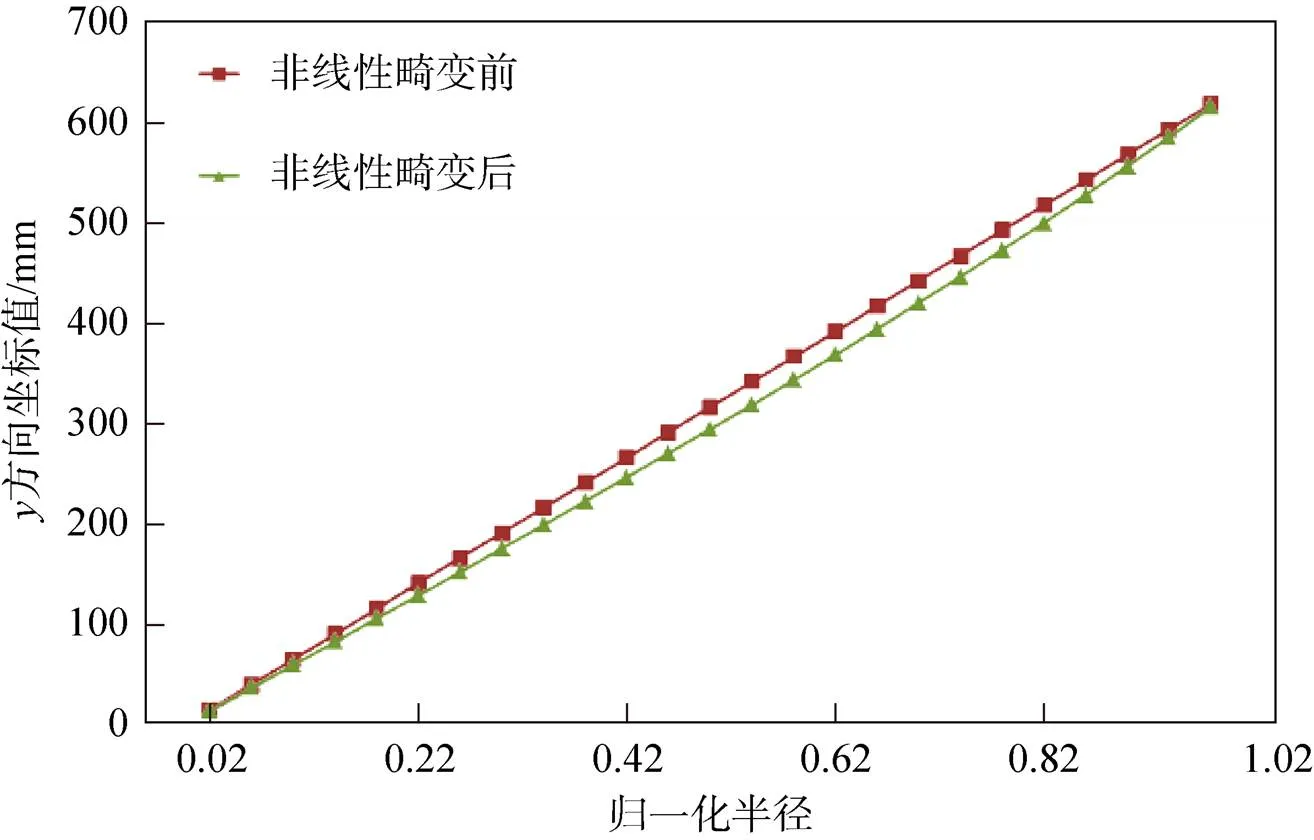
图2 非线性误差关系
2 检测工艺流程
反射镜的有效通光孔径,是指满足光学系统成像要求且在干涉测量阶段可产生有效干涉条纹的区域,一般包括外边缘通光口径(1)和中心孔通光口径(2)两个参数,如图3所示。其中,mir为待测非球面反射镜的镜面坐标系参考面,CCD为干涉仪CCD坐标系所对应的坐标参考面,后续的坐标系均是在mir和CCD两个参考面上建立的。

图3 非球面反射镜有效通光口径
对大口径非球面反射镜的有效通光口径进行检测,工艺流程如图4所示。

图4 检测工艺流程图
由于在非球面反射镜检测过程中,干涉仪所生成的干涉图形是以CCD尺度作为参照,无法通过直接测量的手段来获取镜面的实际有效通光口径。所以该方法的核心思想是首先计算出镜面有效通光口径在CCD尺度下所对应的通光口径值,然后再根据非线性误差关系,反演出镜面尺度下的实际有效通光口径。其中的几个主要步骤如下所述:
(1)光线追迹
由于在干涉仪内光路结构中多采用球面、平面等光学元件,几乎不引入非线性误差,可以忽略[20],干涉仪CCD坐标点位置与其标准参考镜镜头平面上的坐标点位置近似为一一对应关系。
基于上述等效关系,首先在商用光学设计软件中,建立基于补偿法的干涉检测光路模型。在模型中建立过程中,为了提高追迹精度,一是将补偿元件的实测参数,包括曲率半径、镜间距等代入;二是设置测试光束的边缘光线刚好通过非球面反射镜设计的外边缘有效通光口径。然后在实际光线追迹过程中,可以取干涉仪标准参考镜镜头平面上的一系列点,在软件中追迹各个离散点经过补偿检测系统后投影至待测镜镜面上的点坐标。最后,就可以得到一系列反射镜径向位置上的镜面坐标点及与之对应的干涉仪参考镜镜面坐标点,并对其进行归一化处理。
(2)建立非线性误差关系
因为非线性误差在非球面镜面坐标系中对光轴点中心对称,且只与某点离开光轴点的径向距离r有关。也就是说,离开光轴点的距离相同,则非线性误差的大小相同。
设镜面坐标M(R)与干涉仪CCD坐标C(r)间的函数关系为(r)=(0,1,2, …,a,r),则根据最小二乘拟合原理,使其满足

式中a(=0, 1, 2, ···,)为待定系数;为函数关系式中的最高次数;为采样点数据个数。
则令
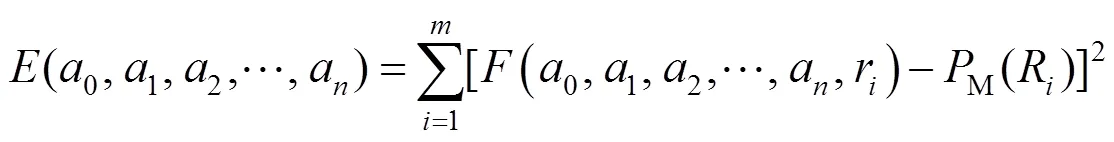
求解方程组

得出待定系数a,从而确定(r)的具体表达式。
为了避免方程组出现病态的问题,通常采取正交多项式的线性组合来做最小二乘拟合,求解多项式的各项系数[21]。
于是,在任意一条直径方向上,镜面坐标序列点{M()}与干涉仪CCD坐标序列点{C()}间的非线性误差函数关系可以表示为
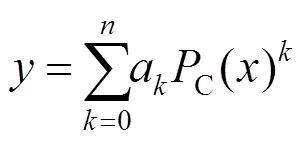
式中为反射镜镜面径向的坐标;为干涉仪CCD坐标镜面径向的坐标;C的函数形式需要根据实际的测试系统和用途来综合确定。
(3)计算反射镜有效通光口径
首先标定出干涉仪CCD的平均分辨率,事先在待测反射镜直径方向上标记出轴和轴并制作标记点,如图5所示,并通过三坐标或激光跟踪仪[22]的方法来标定这些标记间的距离;然后调整测试光路,使其干涉成像,在干涉图中记录标记点间的像素数量。为了提高测试精度,可以在径向增加采样线的数量,最后对像素进行平均记为avg。

图5 标记示例
则待测反射镜的有效通光口径为

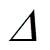
根据式(4)的结果,对于直径方向上任意一点,对其进行归一化可得

式中C为非线性误差拟合关系函数,根据实际情况,可选取多项式函数、指数函数等;为归一化系数,在0~1间取值。
3 测试试验
在测试试验中,测试对象为某空间型号相机中的主反射镜,曲率半径为3 477.2mm,非球面系数为–0.9827,反射镜口径设计值为1 260mm,其中外边缘有效通光口径设计值为1 250mm,中心孔有效通光口径设计值为300mm。
采取基于球面波入射的会聚光零位补偿器对该反射镜进行竖直状态下的面形检测,检测光路和设计参数分别如图6和表1所示。其中会聚光零位补偿器由两片透镜所组成,干涉仪入射的球面波经过零位补偿器折射后,产生一束与待检非球面反射镜波前误差相吻合的测试波前,沿待检非球面反射镜的法线反向垂直入射后原路返回,从而实现了对非球面反射镜的面形检测。

图6 检测光路
表1 光学设计参数

Tab.1 Optical design parameters
3.1 建立非线性误差关系
按照光线追迹的方法,对球面波入射到零位补偿器上的第一个平面端进行采样,在半径方向上等间隔取50个离散点进行光线追迹,获取任一点经过补偿成像系统后投影到镜面上的坐标点,建立数据矩阵,以此作为输入,按照式(4),进行非线性误差畸变曲线拟合,如图7所示。
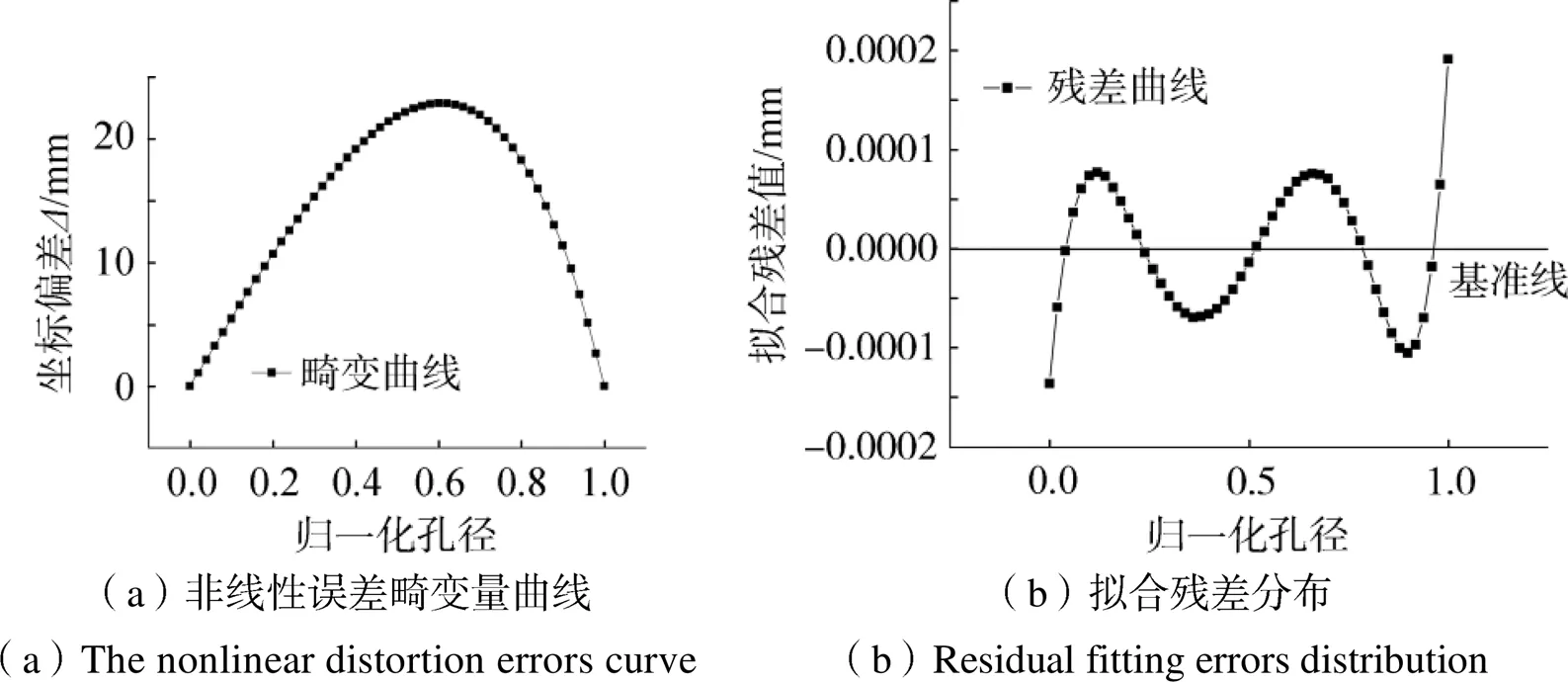
图7 非线性误差拟合
从图7可以看出,在非球面反射镜的中心原点及边缘处,不存在非线性误差。经计算,在约2/3环带附近,非线性误差最大,最大坐标偏差量数值约23.3mm。
3.2 实测结果
首先通过干涉条纹调整实体镜面上的标记处于镜面轴、轴上,事先量取标记之间的实际长度;然后在干涉图上分别测量标记间的像素数量N1N1和整个干涉图的像素数N2N2,如图8所示;最后通过式(5)和式(6)计算实际的有效通光口径。

图8 有效通光口径测试
经过多次测试,在未考虑非线性误差畸变时,反射镜外边缘通光口径平均值为1 250mm、中心孔通光口径为330mm;考虑到非线性误差畸变,进行实际的通光口径反算,可以得到反射镜外边缘有效通光口径平均值为1 248mm、中心孔通光口径为302mm。
3.3 对系统MTF的影响
将测试过程中未经处理的干涉图和经过非线性误差校正后的干涉图形分别代入到光学系统中进行仿真分析,得到光学系统的MTF曲线变化,如图9所示。
根据分析结果,直接将未经过处理的图形代入到光学系统中计算MTF,系统各视场的平均MTF从理论值0.350@71.5线对/mm降低到0.330@71.5线对/mm。而将经过非线性误差校正后的镜面图形及数据代入到系统中计算MTF,系统各视场的平均MTF从原始的0.350@71.5线对/mm降低到0.345@71.5线对/mm。

图9 系统MTF仿真分析
两种镜面数据输入所带来的误差为0.015,其中反射镜边缘口径的误差较小,对系统MTF判别的影响不大;中心孔有效通光口径的偏差较大,若直接沿用原干涉图形中所标志的通光口径数值,将会对实际的光学系统成像性能做出错误的评估。
3.4 测试误差分析
大口径反射镜有效通光口径测试误差主要受测试过程中所用的干涉仪分辨率影响,可以表示为
δ=[(+δ)×(+δ)]–=Aδ+Nδ+δδ(7)
式中为通光口径的测试误差;为选定干涉仪测试下的CCD平均分辨率;为平均分辨率的测试误差,经多次平均测试后,误差量级在0.005以内,可以忽略不计;为像素数的判读误差,取1~2。
通光口径的测试误差主要由Aδ来确定
=Aδ (8)
如对于口径1m的非球面反射镜来说,采用1 000像素×1 000像素分辨率的干涉仪测试,干涉图布满整个CCD视场时,分辨率近似为1mm/像元,则通光口径的最大测试误差为单边2mm。
4 结束语
1)空间相机主镜多采用补偿法进行面形检测,在过程检测中,利用文中所提方法对反射镜的有效通光口径进行检测,具有定量化、控制精度高的特点,且在反射镜多次迭代加工过程中,可以通过干涉图形直接计算出反射镜的有效通光口径数值,便于在工艺过程中对其进行实时有效监控。
2)在测试中,边缘通光口径的非线性畸变量为1mm,对系统MTF的影响不大;但中心孔口径的非线性畸变量达到了14mm,导致非线性误差畸变前后的系统MTF偏差达到了0.013,对正确评估光学系统的成像性能带来了很大的误差。
3)本方法的测试误差主要取决于干涉仪的分辨率限制。目前主流的商用干涉仪分辨率为1 000像素×1000像素和2 000像素×2 000像素两种,后续还有更高分辨率的干涉仪产品陆续上市,所以应用该方法可以满足米级及更大口径反射镜的通光口径精度控制需求。
4)该方法不仅适用于同轴非球面反射镜有效通光的测量,辅以必备的辅助工装及标定仪器,也可以满足离轴非球面反射镜有效通光口径的测量。
[1] 王小勇. 空间光学技术发展与展望[J]. 航天返回与遥感, 2018, 39(4): 79-86. WANG Xiaoyong. Development and Prospect of Space Optical Technology[J]. Spacecraft Recovery & Remote Sensing, 2018, 39(4): 79-86. (in Chinese)
[2] 张博文, 王小勇, 赵野, 等. 天基大口径反射镜支撑技术的发展[J]. 红外与激光工程, 2018, 47(11): 1113001(1)-1113001(9). ZHANG Bowen, WANG Xiaoyong, ZHAO Ye, et al. Progress of Support Technique of Space-based Large Aperture Mirror[J]. Infrared and Laser Engineering, 2018, 47(11): 1113001(1)-1113001(9). (in Chinese)
[3] 李果, 孔祥皓. 静止轨道高分辨率光学成像卫星发展概况[J]. 航天返回与遥感, 2018, 39(4): 55-63. LI Guo, KONG Xianghao. Overview and Development Trends of High-resolution Optical Imaging Satellite at Geostationary Orbit[J]. Spacecraft Recovery & Remote Sensing, 2018, 39(4): 55-63. (in Chinese)
[4] 阮宁娟, 庄绪霞, 李妥妥, 等. 空间光学遥感系统全链路仿真与分析[J]. 航天返回与遥感, 2013, 34(6): 34-43. RUAN Ningjuan, ZHUANG Xuxia, LI Tuouo, et al. End to End Simulation and Analysis of Space Optical Remote Sensing System[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(6): 34-43. (in Chinese)
[5] MCCOMAS B K. Toolkit for Remote-sensing Analysis, Design, Evaluation and Simulation[J]. SPIE, 2004, 5420: 75-84.
[6] SCHOTT J R, GERACE A D, BROWN S D, et al. Modeling the Imaging Performance of the Landsat Data Continuity Mission Sensors[J]. SPIE, 2011, 8153: 81530F-1-81530F-1.
[7] 杜航, 李圣怡, 宋辞. CCOS边缘效应的小研抛盘修形修正方法[J]. 国防科技大学学报, 2015, 37(6): 30-33. DU Hang, LI Shengyi, SONG Ci. Correct Method of the CCOS Edge Effect by Little Tool Figuring[J]. Journal of National University of Defense Technology[J]. 2015, 37(6): 30-33. (in Chinese)
[8] KIM D, WON P W, KIM S W, et al. Parametric Modeling of Edge Effects for Polishing Tool Influence Functions[J]. Optic Express, 2009, 17(7): 5656-5665.
[9] 邓伟杰, 张峰, 郑立功. 边缘效应的去除函数模型及实验[J]. 红外与激光工程, 2011, 40(9): 1743-1748. DENG Weijie, ZHANG Feng, ZHENG Ligong. Removal Function Model and Experiment of Edge Effect[J]. Infrared and Laser Engineering, 2011, 40(9): 1743-1748. (in Chinese)
[10] NOVAK M, ZHAO C, BURGE J H. Distortion Mapping Correction in Aspheric Null Testing[J]. SPIE, 2008, 7063(706313): 1-8.
[11] BURGE J H. Advanced Techniques for Measuring Primary Mirrors for Astronomical Telescopes[D]. Tucson: The University of Arizona, 1993.
[12] ZENG Xuefeng, ZHANG Xuejun, XUE Donglin, et al. Mapping Distortion Correction in Freeform Mirror Testing by Computer-generated Hologram[J]. Applied Optics, 2018, 57(34): 56-61.
[13] KIM T, BURGE J H, LEE Y, et al. Null Test for a Highly Paraboloidal Mirror[J]. Applied Optics, 2004, 43(18): 3614-3618.
[14] 曾雪峰, 闫锋, 薛栋林, 等. 计算全息图补偿检测离轴非球面中的投影畸变校正技术[J]. 中国激光, 2013, 40(11): 1109003(1)-1109003(5). ZENG Xuefeng, YAN Feng, XUE Donglin, et al. Distortion Correction in Testing of Off-axis Asphere with Computer-generated Hologram[J]. Chinese Journal of Lasers, 2013, 40(11): 1109003(1)-1109003(5). (in Chinese)
[15] 陈哲, 张星祥, 陈长征, 等. 大口径离轴非球面补偿检测的畸变校正[J]. 中国激光, 2015, 42(10): 1008001. CHEN Zhe, ZHANG Xingxiang, CHEN Changzheng, et al. Distortion Mapping Correction in Testing of Large Off-axis Aspherical Mirrors with Null Lens[J]. Chinese Journal of Lasers, 2015, 42(10): 1008001. (in Chinese)
[16] 兰海滨, 王平, 龙腾.图像拼接中相机镜头非线性畸变的校正[J]. 光学精密工程, 2009, 17(5): 1196-1202. LAN Haibin, WANG Ping, LONG Teng. Nonlinear Aberration Correction of Lens in Image Mosaic[J]. Optics and Precision Engineering, 2009, 17(5): 1196-1202. (in Chinese)
[17] 叶峰, 王敏, 陈剑东, 等. 共面点的摄像机非线性畸变校正[J]. 光学精密工程, 2015, 23(10): 2962-2970. YE Feng, WANG Min, CHEN Jiandong, et al. Camera Nonlinear Distortion Correction Based on Coplanar Points[J]. Optics and Precision Engineering, 2015, 23(10): 2962-2970. (in Chinese)
[18] MACGOVERN A J, WYANT J C. Computer Generated Holograms for Testing Optical Elements[J]. Applied Optics, 1971, 10(3): 619-624.
[19] 伍凡. 非球面零检验的Offner补偿器设计[J]. 应用光学, 1993, 14(3): 8-11. WU Fan. Design of Reflective Offner Compensator for Null Testing of Aspheric Surface[J]. Journal of Applied Optics, 1993, 14(3): 8-11. (in chinese)
[20] 李锐钢, 郑立功, 薛栋林, 等. 大口径高次、离轴非球面干涉测量中投影畸变的标定方法[J]. 光学精密工程, 2006, 14(4): 533-538. LI Ruigang, ZHENG Ligong, XUE Donglin, et al. Calibration Method for Projection Distortion in Interferometric Testing High Order and Off-axis Aspheric Surface with Big Aperture[J]. Optics and Precision Engineering, 2006, 14(4): 533-538. (in Chinese)
[21] ZHAO C, BURGE J H. Orthonormal Vector Polynomials in a Unit Circle, Part I: Basis Set Derived from Gradients of Zernike Polynomials[J]. Optics Express, 2007, 15(26): 18014-18024.
[22] 陈新东, 李锐钢. 非球面Null Lens补偿检测中采用激光跟踪仪测量几何参数方法研究[J]. 中国激光, 2015, 42(5): 0508007(1)-0508007(7). CHEN Xindong, LI Ruigang. Research on Geometric Parameter Measurement Method Using Laser Tracker in Null Lens Asphere Testing[J]. Chinese Journal of Lasers, 2015, 42(5): 0508007(1)-0508007(7). (in Chinese)
A Quantitative Testing Method for the Effective Clear Aperture of Aspheric Mirrors
MENG Xiaohui1,2ZHANG Jiyou1,2*WANG Yonggang1,2LI Ang1,2ZHOU Yuming1,2LI Wenqing1,2
(1 Beijing institute of space Mechanics & Electricity, Beijing 100094, China)(2 Optical Ultraprecise Processing Technology Innovation Center for Science and Technology Industry of National Defense, Beijing 100094, China)
The effective clear aperture is an important parameter of aspheric mirrors, but there were many problems existed such as the difficulty of quantitative testing and larger test errors. Then in the subsequent stage of ground installation and adjustment, it was often difficult to correctly assess the system imaging quality. In order to solve these problems, a testing method based on nonlinear correction was proposed. Firstly, different data were acquired in interferometer CCD and mirror coordination systems using the ray tracing method. Then the nonlinear relationship between the mirror under test and the surface map was established. Finally, the effective interference fringe pattern in the scale of the interferometer CCD coordinate system was used as the input to inversely calculate the actual effective aperture of the mirror under the mirror scale. A space camera primary mirror with diameter larger than one meter was tested using this method, which accuracy can reach 1 pixel corresponding mirror length, and the testing accuracy is mainly depended on the interferometer CCD average resolution. The optical system modulation transfer function was separately analyzed by taking the original and corrected maps, and the MTF value offset was 0.013@71.5lp/mm. The results show that it is useful to test the effective clear aperture timely in manufacture process, and can also appraise the optical system performance in optical alignment process rightly, which has very important meanings in advanced manufacturing field of space optical aspheric mirrors.
optical fabrication; optical test; aspheric mirror; effective clear aperture;nonlinear error correction; space optical camera
TH706
A
1009-8518(2020)05-0038-09
10.3969/j.issn.1009-8518.2020.05.005
2020-03-25
国防科技创新特区项目(19-163-18-ZT-013-023-01)
孟晓辉, 张继友, 王永刚, 等. 一种非球面反射镜有效通光口径的定量化检测方法[J]. 航天返回与遥感, 2020, 41(5): 38-46.
MENG Xiaohui, ZHANG Jiyou, WANG Yonggang, et al. A Quantitative Testing Method for the Effective Clear Aperture of Aspheric Mirrors[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(5): 38-46. (in Chinese)
孟晓辉,男,1985年生,2010年获中科院南京天文光学技术研究所天体物理专业硕士学位,高级工程师。研究方向为空间光学先进制造技术。E-mail:mrmeng_508@163.com。
张继友,男,1978年生,2006年获中科院成都光电技术研究所测试计量技术及仪器专业博士学位,研究员。研究方向为空间光学先进制造技术。E-mail:jyzhang0627@163.com。
(编辑:王丽霞)
