基于模糊预测的INS/视觉无人机自主着陆导航算法*
2020-01-02李亚贵李宇峰张舰栋
洪 亮,章 政,2,3*,李亚贵,李宇峰,张舰栋
(1.武汉科技大学信息科学与工程学院,武汉 430081;2.武汉科技大学机器人与智能系统研究院,武汉 430081;3.武汉科技大学冶金自动化与检测技术教育部工程研究中心,武汉 430081)
自主着陆是无人机自主飞行系统中的重要环节,通过机载导航设备获取实时、精确的位姿信息是实现无人机安全、有效着陆的前提和基础[1]。相比于GPS导航方式[2],基于视觉的无人机着陆导航方式可全覆盖、独立获取着陆点周围高精度的三维空间反馈信息,对环境要求较低,具有抗干扰能力强、精度高和功耗低等特点[3]。目前,惯性导航系统INS(Inertial Navigation System)与视觉传感器构成INS/视觉组合导航系统已成为无人机自主着陆导航系统设计的主要趋势[4-5]。
对于基于INS/视觉的无人机自主着陆导航系统,常采用卡尔曼滤波KF(Kalman Filter)实现INS与视觉传感器的数据融合。文献[6]由视觉位姿估计系统得出飞行器的位姿信息,通过卡尔曼滤波实现位置、姿态匹配;文献[7]构建了一种非线性滤波器实现了惯导误差估计,在提高算法效率的同时有效地避免了无迹卡尔曼滤波中由于矩阵开方运算导致的滤波失效问题;文献[8]提出了一种基于图像辅助惯导的扩展卡尔曼滤波方法,使得基于视觉辅助惯导的组合导航系统逐渐成为一种新的导航模式;文献[9]通过多估计中心的加权并将扩展卡尔曼滤波与单目视觉位姿估计相结合,提高了无人机的位姿估计精度。上述研究主要是利用视觉传感器的观测数据修正INS的估计误差,再结合卡尔曼滤波实现无人机的位姿估计,由此避免INS定位误差随时间累积的缺陷。
然而,在无人机实际着陆过程中,机载摄像头获取着陆点附近图像信息是一个动态测量过程,其视觉观测数据会随着时间和空间而变化且包含了飞行环境中的各种干扰信息。因此,通过透视投影模型解算出的视觉观测数据存在观测噪声与解算误差[10],直接融合INS和视觉的数据易导致系统额外误差[11]、位姿状态估计不收敛[12-13]等问题。此外,由于受到机载传感器低主频、无硬件浮点运算等限制,视觉观测数据的更新周期长,从而影响无人机位姿估计的实时性。
基于上述分析,考虑到模糊逻辑[14]可有效处理机载摄像头获取观测数据的时变性和不确定性,本文设计了一种基于模糊预测的INS/视觉无人机自主着陆导航算法。首先,采用模糊数描述机载摄像头解算所得的观测数据,在INS数据更新的同时,构造基于历史观测数据的模糊预测模型,由此预测机载摄像头当前时刻的观测数据;然后,设计基于状态量同步更新的卡尔曼滤波器,对INS产生的误差进行修正,得到无人机的位姿估计,从而避免直接融合INS与视觉数据导致系统额外误差的问题,提高了无人机的位姿估计精度;最后,通过基于四旋翼无人机平台的实测实验验证了本文算法的有效性和实时性。
1 基于INS/视觉的无人机自主着陆导航系统设计
1.1 自主着陆导航系统的坐标系定义
本文所设计的INS/视觉无人机自主着陆导航系统主要包括:四旋翼无人机、机载摄像头和着陆地标,其位姿关系如图1所示。
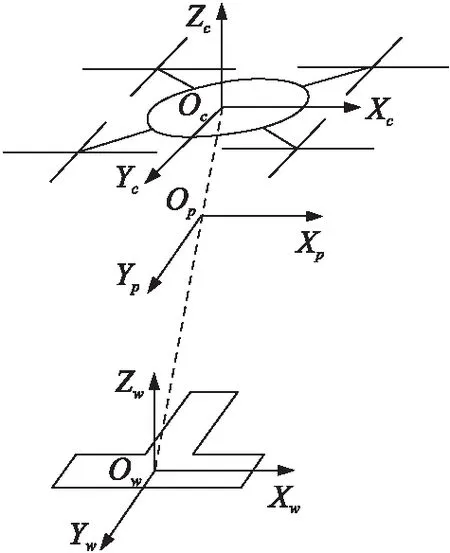
图1 坐标系对应关系
Oc-XcYcZc为四旋翼无人机和机载摄像头的坐标系,坐标系原点Oc为无人机的机体重心。X轴和Y轴位于无人机机体平面内,Y轴指向无人机前进方向,X轴指向无人机左侧方向,Z轴指向无人机上升方向。
Op-XpYp为图像坐标系,平行于无人机机体平面,Y轴指向无人机前进方向,X轴指向无人机左侧方向。
Ow-XwYwZw为着陆地标坐标系,坐标系原点Ow为着陆地标的几何中心。X轴和Y轴位于着陆地标平面内,Y轴指向地理正北方向,X轴指向地理正西方向,Z轴垂直于着陆地标平面向上。
1.2 基于INS/视觉的无人机自主着陆导航算法
针对INS/视觉的无人机自主着陆系统的特点,将模糊预测用于导航算法中,算法结构图如图2所示。

图2 基于INS/视觉的无人机自主着陆导航算法
首先,对图像中的着陆地标进行特征点提取,通过视觉解算得到无人机在地标坐标系下的位置观测数据。针对视觉观测数据存在不确定性问题,采用三角模糊处理视觉解算得到的观测数据。然后,针对无人机非线性、强耦合和静态不稳定的特性,考虑到机载计算机的处理能力有限,在惯导数据更新的同时,利用模糊预测的方法预测视觉传感器的位置观测数据。最后,在得到视觉观测数据的一步预测值后,通过卡尔曼滤波器修正惯导的加速度零偏、速度误差和位置累计误差,得到用于无人机位置反馈控制的最优估计值,达到无人机自主着陆中对位姿估计实时性的要求。
2 基于模糊预测的INS/视觉无人机位姿估计算法
2.1 视觉观测数据解算
对机载摄像头拍摄的图像进行Harris特征点检测,提取着陆地标的特征点。根据透视投影模型和刚体旋转平移的坐标变换原理,结合图1所示的坐标系对应关系,着陆坐标系中的特征点(xw,yw,zw)与其对应图像坐标中像素点(u,v)的关系如下:
(1)
式(1)中zc为特征点(xw,yw,zw)在相机坐标系的坐标,K为相机参数,R,T为无人机相对于地标的旋转矩阵和偏移矩阵,分别为:
R=
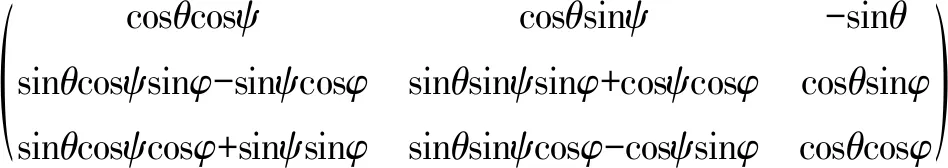
(2)
(3)
式(2)中,θ,φ,ψ分别为俯仰角、横滚角和偏航角,式(3)中,Tz为无人机相对于地标的高度,Tx和Ty为无人机相对地标的水平偏移量。
由于zc和摄像头参数K为已知量,因此根据若干组地标中特征点(xw,yw,zw)在图像中的像素(u,v),就可以求得旋转矩阵R和偏移矩阵T,获取无人机相对于地标的姿态和位置信息。

图3 观测量预测及状态同步更新
2.2 基于模糊预测的视觉观测数据分析及处理

以X轴位置的观测数据为例,考虑到二次函数可以表征大部分目标的运动轨迹,在短时间内摄像头的位置观测数据Tx(t)采用式(4)所示的模糊序列模型描述:
Tx(t)=r0+r1t+r2t2+ε
(4)
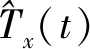
(5)
(6)
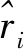
取k+1时刻以前的L个时刻的摄像头历史位置观测数据Tx1,Tx2,…,TxL,令mt=max{Txt-1,Txt,Txt+1},nt=min{Txt-1,Txt,Txt+1}(t=2,3,…,L-1),m1=max{Tx1,Tx2},n1=min{Tx1,Tx2},mL=max{TxL-1,TxL},nL=max{TxL-1,TxL}。将这L个数据进行模糊处理,构成如式(7)所示的一组三角模糊数st(x)。
(7)

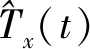
(8)
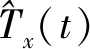
(9)
式(9)中,权重ω={ω0,ω1,ω2}由普通线性回归给出:
(10)
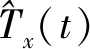
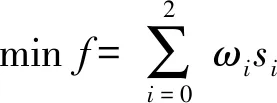
(11)
2.3 基于卡尔曼滤波器的状态量同步更新
以Ow-XwYwZw着陆地标坐标系为导航坐标系,在INS更新时,利用摄像头观测数据对无人机INS估计出的位置状态进行误差修正。
无人机在降落阶段需要获取OwXw、OwYw、OwZw方向上的3个位置与3个速度状态量,选取无人机的状态量为:
(12)

(13)
由匀加速直线运动方程,得到系统状态方程在k时刻离散化为:
X(k)=AX(k-1)+BU(k)+Γω
(14)
式(14)中系统状态转移矩阵A、驱动矩阵B、过程噪声分布矩阵为Γ为:
(15)
(16)
(17)
其中DT为摄像头观测数据的更新周期。
Zk=HXk+Vkν
(18)
式中的系统状态量为全观测,故状态观测矩阵H=I6×6。
系统过程噪声协方差矩阵Qk与静态观测噪声矩阵Rk需要根据实际使用来整定:
(19)
(20)
先验协方差矩阵与卡尔曼滤波增益更新的更新表达式为:
P(k+1|k)=AP(k|k)AT+ΓQΓT
(21)
K(k+1)=P(k+1|k)HT[HP(k+1|k)HT+R]-1
(22)

(23)
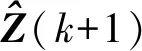
(24)
式(24)中,ΔT为当前INS的更新时刻k+1与最近一次观测传感器的更新时刻ko的时间间隔。ΔT和ko均来自计算机系统的测量时间。
后验协方差矩阵更新如下:
P(k+1|k+1)=[I6×6-K(k+1)H]P(k+1|k)
(25)
根据上述分析,本文设计的基于模糊预测的INS/视觉无人机位姿估计算法框图如图4所示。
在无人机INS/视觉组合导航降落系统中,针对摄像头观测传感器数据滞后特性引起的状态估计误差甚至发散问题,本文利用模糊预测的方法,同步预测滞后的观测传感器数据。考虑到低成本微处理器的实际处理能力有限,利用卡尔曼滤波对INS的累计误差进行修正,减小了计算量,保证了融合算法的实时性。
3 组合导航系统设计与实验
本文自主设计了无人机自主着陆导航实验平台并设计了三组实验,验证了本文算法的实时性、有效性和实用性。
3.1 实验配置介绍
无人机自主着陆导航实验平台包括四旋翼无人机和着陆地标,如图5所示。四旋翼无人机由飞行控制器、电子调速器、无刷电机、螺旋桨、机架、电池、低压报警器、遥控器和视觉模块等部分组成。四旋翼无人机的总重量0.865 kg,机体对角线轴距为33 cm,高12 cm。
四旋翼无人机的系统硬件结构如图6所示,飞行控制器采用32位微处理器STM32F103RCT6,主频为72 MHz。姿态传感器采用六轴陀螺仪加速度计传感器MPU6050,磁力计采用IST8310,气压计为SPL06-001。视觉模块由OV5647摄像头模组和“树莓派”微型计算机组成。微型计算机的CPU采用Broadcom BCM2837,内存1G,安装了Raspbian操作系统和OpenCV 3.4.1视觉开发库。

图6 飞控系统结构示意图
本文在每帧图像中选取8个特征点,求解无人机的偏移矩阵T,然后通过串口实时发送给飞行控制器。飞行控制器中INS更新频率为200 Hz,根据实际调试,选取过程噪声矩阵Qk与观测噪声矩阵Rk中参数a、b、c、d分别为2.0×10-6、0.015、0.075、2.5,贴近度h0取0.7。
3.2 实验及结果分析
①实时性对比实验
在实时性对比实验中,以高度方向位置融合为例,大约1 s左右将无人机快速拉至降落引导地标正上方约90 cm高度位置,得到同一实验条件下本文组合导航算法和常规卡尔曼算法的实验数据如图7所示,算法的收敛时间和均方根误差如表1所示。

表1 实时性对比实验的数据分析
从图7(a)和表1的实验数据可以看出,本文设计的无人机组合导航算法得到的高度位置估计值相比于常规卡尔曼滤波算法,能一次性快速地跟踪视觉传感器解算出的高度变化过程,并且迅速收敛。结合图7(b)的实验数据,在动态过程中,由于观测传感器更新周期长,短时间内原始观测高度更新不及时,而经模糊预测得到的观测数据能够较为准确地描述观测数据的变化。使得图7(a)中组合导航得到的高度估计值相位超前于视觉传感器观测的高度,提高了位置估计的实时性。

图7 实时性对比实验
②无人机实际飞行实验
在无人机实际飞行实验中,无人机初始状态为定点悬停状态,位于(10,-10,40),3 s后利用遥控器依次飞行至(10,10,40)、(-10,10,40)、(0,0,40)。悬停3 s后,控制遥控器油门动作位,让无人机在高度方向做快速机动动作,最后,悬停在(0,0,22)处。无人机实际飞行实验结果如图8所示,X、Y、Z三方向的均方根误差和误差最大值如表2所示。
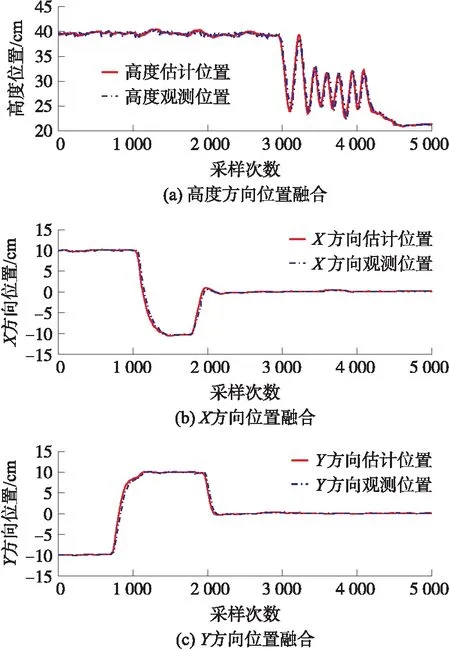
图8 实际飞行融合实验数据

方向误差最大值/cm常规算法本文算法均方根误差常规算法本文算法XYZ4.75.96.24.65.34.10.160.190.150.110.130.09
表2的数据表明本文组合导航算法相比于常规算法融合得到的位置估计精度更高,由图8的位置融合实验结果可知,静态时惯导估计状态和摄像头的观测状态基本吻合,经过融合得到的估计状态数据会更加平滑,受观测传感器自身噪声影响,融合得到的估计状态数据会有一定的波动,其波动范围远小于观测状态数据自身的波动。观察由静止到运动的过程,摄像头得到的观测状态存在一定的滞后现象,动态过程中融合得到的估计状态相位始终超前于摄像头的观测状态。观察动态到静止的运动过程可知,融合得到的位置估计会迅速收敛到位置观测量。本文设计的组合导航算法提高了位姿估计的实时性,同时位姿估计数据能保证长时间收敛。
③自主着陆实验
在自主降落实验中,降落地标安装在移动平台上,利用遥控器控制无人机飞行在平台上方1.5 m后,将自主降落对应通道打到高位,无人机自动完成着陆控制。经过多次实验,着陆后无人机与地标中心的平均偏移误差如表3所示。

表3 不同速度下降落误差对比
表3的实验数据表明了本文INS/视觉组合导航算法相比于常规算法能够为无人机的自主降落控制提供更为实时、准确的反馈数据,满足四旋翼无人机的自主着陆要求。
4 结束语
在INS/视觉导航无人机自主着陆导航系统中,由于视觉观测数据存在不确定性噪声、更新慢等问题,导致组合导航算法的精度和实时性受到限制。鉴于此,本文设计了一种基于模糊预测的INS/视觉无人机自主着陆导航算法。考虑到机载处理器的硬件限制,本文从卡尔曼滤波模型出发,采用三角模糊数处理视觉观测数据,减小了观测噪声和解算误差带来的滤波估计误差。在INS数据更新时,利用模糊预测的方法同步预测滞后的视觉观测传感器数据,相比于常规卡尔曼滤波算法,提高了无人机位姿估计的实时性。实测实验结果表明利用本文设计的组合导航算法能实时、准确地估计无人机相对于地标的位姿信息,满足无人机自主着陆所需数据的实时性与动态跟踪精度要求,为基于INS/视觉的无人机自主着陆系统提供了一种简单可靠的组合导航算法。
