EMAT环形线圈阻抗的解析建模与计算*
2020-01-02周进节崔世杰吴旭东
周进节,崔世杰,郑 阳,吴旭东
(1.中北大学机械工程学院,太原 030051;2.中国特种设备检测研究院,北京 100029)
铝合金构件在航空航天、交通及电力等领域得到了广泛的应用,因此对这些铝合金构件进行无损检测具有重要意义。电磁超声检测因其非接触、无需耦合剂等优点,非常适合对铝合金构件进行检测[1-3]。在对铝合金构件进行检测时,电磁超声换能器是基于洛伦兹力进行电-声能量转换的。线圈的阻抗直接影响功放传输给传感器的能量[4]。线圈阻抗与其形状、材料、尺寸参数等有关。因此,建立线圈理论模型并计算其阻抗,不仅便于理解线圈阻抗的物理意义及变化规律,还可为换能器的设计及提高电-声能量转换效率提供一定的理论指导。
在涡流传感器、电磁超声传感器等电磁类传感器阻抗计算方面,国内外学者进行了大量的研究。1968年,C.V.Dodd等人针对矩形截面线圈在双导体平面和双导体板中产生的矢量磁位进行了解析建模,并通过推导得到交变电流在试件中产生的涡流、磁场、力以及线圈阻抗等物理量的积分表达式[5]。1970年,Dodd C V对线圈位于多层介质的情况进行了建模与计算,求得了线圈的阻抗及在试块中产生的涡流。1984年,日本学者Kawashima应用Dodd C V电涡流模型与声场计算方法得到了单匝矩形截面线圈在铝板中产生的纵波和横波分布[6]。2003年,Theodoulidis T P针对Dodd C V电涡流模型中无穷积分计算时间长的问题,提出将无穷积分转化为无穷级数的方法。该方法不仅简化了模型的计算过程,而且提高了计算效率[7]。2007年,于亚婷等人采用TREE方法把电涡流传感器线圈的阻抗积分表达式转化为级数表达式,并进行了有限元仿真与计算[8]。2011年,郝宽胜、黄松岭等人对平面螺旋线圈EMAT进行建模,并分析计算了脉冲磁场和输入阻抗[9]。2013年,翟国富、康磊等人应用C.V.Dodd电涡流模型建立了单层螺旋线圈EMAT模型[10],并通过该模型计算了试件中的涡流、洛伦兹力及线圈阻抗。2016年,黄一民、吴德会等人提出了一种位于导体上方正交折线线圈的阻抗解析建模方法,并根据影响阻抗的各个变量绘制阻抗平面图[11]。2018年,吴德会等人提出一种包含误差补偿项的任意折线线圈阻抗解析新模型[12]。
但目前对电磁超声换能器解析建模研究的报道中,尚未详细研究不同求和次数和截断半径对于阻抗计算结果的影响。为此,本文对环形线圈电磁超声换能器进行建模,根据电磁场理论导出线圈阻抗积分表达式,然后采用TREE法将阻抗积分表达式转化为更加容易求解的级数表达式,着重研究了不同的求和次数和截断半径对阻抗计算的影响,并通过阻抗计算值和测量值的比较,说明了模型的适用性。

图1 模型图
1 理论建模
1.1 模型的建立及前提
根据电磁超声换能器的原理[5,8]建立理论模型,为了使得解析模型便于求解,对实际物理模型进行了简化。3维示意图如图1所示,假定空间中各个求解区域内的媒质均为线性、各向同性的且除线圈区域外,其他区域都当做真空处理;把双层的螺旋形线圈等效为双层的多个同心圆线圈的叠加;忽略线圈的集肤效应和邻近效应;忽略位移电流的作用[5,9-10]。
在圆柱坐标系下线圈的几何模型如下图2所示。求解空间沿z轴方向被分成7个求解区域,用s来表示。s=1、7为空气区域,s=2、4为线圈区域,s=5为基片区域,s=6的区域为试块区域。由于各个求解区域关于z轴对称,所以每个求解区域中的矢量磁位仅有周向分量[5,7,9-10,13]。图中r1N为线圈内径,r2N为线圈外径,N为线圈为线圈匝数。l1、l2、l3、l4为矩形线圈的上下边界。

图2 线圈阻抗求解模型
1.2 阻抗推导与计算
由于解析模型关于Z轴呈旋转对称,针对环形线圈电磁超声换能器阻抗求解模型,麦克斯韦方程组[13]在柱坐标系的所有场量均与周向坐标无关[14]。为求解线圈的阻抗,首先考虑位于被测试样上方的δ函数线圈在各个空间的矢量磁位(MVP)。δ函数线圈将空间区域分成4个求解区域,示意图如图2所示。
δ函数线圈在各个求解区域产生的矢量磁位满足的频域微分方程可表示为[5,7,9-10,14]:

(1)
式中:As(ω,r,z)为矢量磁位、i(ω)为激励电流密度、μs和σs分别为磁导率和电导率、s=1,2,3,4代表四个求解区域。

图3 δ函数线圈解析建模
相邻的求解区域应满足以下两类边界条件[5]:
由于这是一个轴对称问题,r与z无关。因此,可以采用分离变量法,把目标方程转化为一阶贝塞尔方程。
分离变量A(r,z)=R(r)Z(z),将其代入目标方程(1)中,化简得到:
(2)
又因Z只与导体的电导率、磁导率、信号频率有关,将上式中与Z相关的项写为常数:
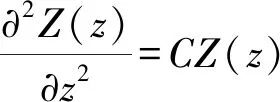


目标方程(2)化简为:
(3)
上式是一个含有参数t的一阶贝塞尔方程,根据一阶贝塞尔方程的通解及其边界条件可以最终得到各个求解区域的解依次为[5,9,14]:
e-tl-tz(e2tl+Q1)dt
(4)
e-tl(etl+Q1e-tz)dt
(5)

e-tl-tz(Q2eT3z+Q3e-T3z)dt
(6)

(7)
式中
在得到δ函数线圈在各个区域产生矢量磁位的基础上,对于双层螺旋线圈在各个求解区域产生的矢量磁位,可通过对δ函数线圈的矢量磁位进行面积积分及上下两层累加合并求得。最终得到求解区域2、区域4内的矢量磁位[9]。
区域2的MVP为
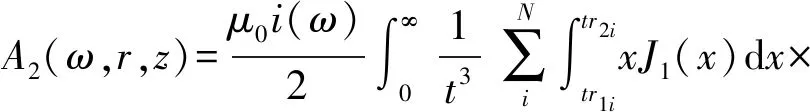
(8)
区域4的MVP为

(9)
在计算线圈的输入阻抗前,首先求解线圈的感应电动势,矩形截面线圈内的感应电动势为[5,10,14]:
(10)
式中:S为线圈横截面积。
双层线圈的感应电动势,可通过对单环矩形截面线圈感应电动势的累加得到,将式(8)、式(9)代入式(10)得:
Vd(ω)=
(11)
再根据欧姆定律,可得到线圈阻抗的积分表达式为[9]:

(12)

直流阻抗Z0为:
1.3 截断区域特征函数展开法
由于式(12)线圈阻抗积分表达式中含有贝塞尔函数的二重广义无穷积分[15-16],这使得阻抗求解的过程变得困难且耗费大量的时间成本。为了使计算变得高效,设置Dirichlet边界条件,即设置截断半径,在距线圈一定的距离R处强加磁场绝缘边界使得在该处的磁场强度为0,再根据偏微分方程理论,将线圈阻抗表达式的积分形式转化为级数表达,使计算变得高效。
转换后的级数表达形式可以表示为:
4[e-tm(l4-l3)-1]+Q1m(e-tml1-e-tml2+e-tml3-e-tml4)2}
(13)
式中
J1(tmR)=0,tmR是J1(x)的第m个根xm,则
tm=xm/R
1.4 阻抗计算
在阻抗级数表达式中含有第一类Bessel函数的零点ti的值且U的计算涉及到对Bessel函数的积分,为了使编程变得简单,这里采用Mathematic软件编程计算。
阻抗级数表达形式与阻抗积分表达形式比较,级数表达式求解速度更快,收敛更易控制。在通过级数表达式求解线圈阻抗时无穷级数限必须被截断,但最优截断点无法预知。
2 实验系统
线圈及被测铝板的参数如表1、表2所示。

表1 双层螺旋线圈的参数

表2 被测铝板试样的参数
为了对双层螺旋线圈的阻抗进行测量,采用了安捷伦公司型号为4195A的阻抗分析仪。在开始测量之前,为保证测量的准确性,需要对阻抗分析仪进行短路、开路、50 Ω负载的测试与校准,然后再对测量系统进行搭建。其中试块及线圈如图4所示,试块厚度为15 mm的铝块。连接实验系统如图5所示,其中包括阻抗分析仪、线圈、铝板,其中阻抗分析仪的型号为4195A。

图4 被测试块及线圈

图5 阻抗分析仪及测量系统
在测量过程中,为保证线圈和铝板之间的提离距离,确保测量的稳定性,在线圈的上方放置一块绝缘塑料薄片,使得线圈与被测试块之间的距离保持不变。
3 结果分析
3.1 计算参数选取
为了取得最优的计算参数,在频率100 kHz下,对不同的截断半径和求和次数进行计算与分析。其中R为线圈的半径,计算结果如图6所示。其中图6(a)展示了截断半径为10R、20R、40R、80R的理论计算结果实部随着求和次数变化的四条曲线,图6(b)展示了截断半径为10R、20R、40R、80R的理论计算结果虚部随着求和次数变化的四条曲线。
对图6进行分析可得,在频率100 kHz下,不同截断半径的阻抗计算结果都随着求和次数的增加趋近于一个固定的值,从而说明了阻抗级数表达式的收敛性。同时通过分析可以得到截断半径越小,收敛的速度越快,更快的趋于固定值。
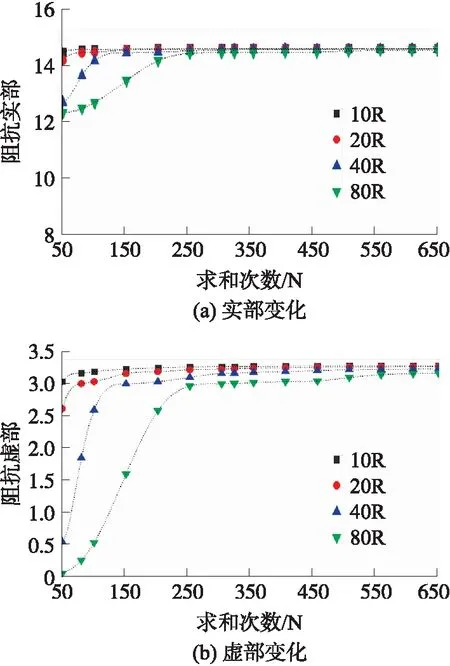
图6 频率为100 kHz时,不同求和次数、不同截断半径的阻抗计算值变化

图7 频率为2 MHz时,不同求和次数、不同截断半径的阻抗计算值变化
为了取得最优的计算参数,证明在不同频率下也存在类似的规律,又分别在频率2 MHz、5 MHz下,对不同的截断半径和求和次数进行计算与分析。理论计算结果如图7和图8所示。
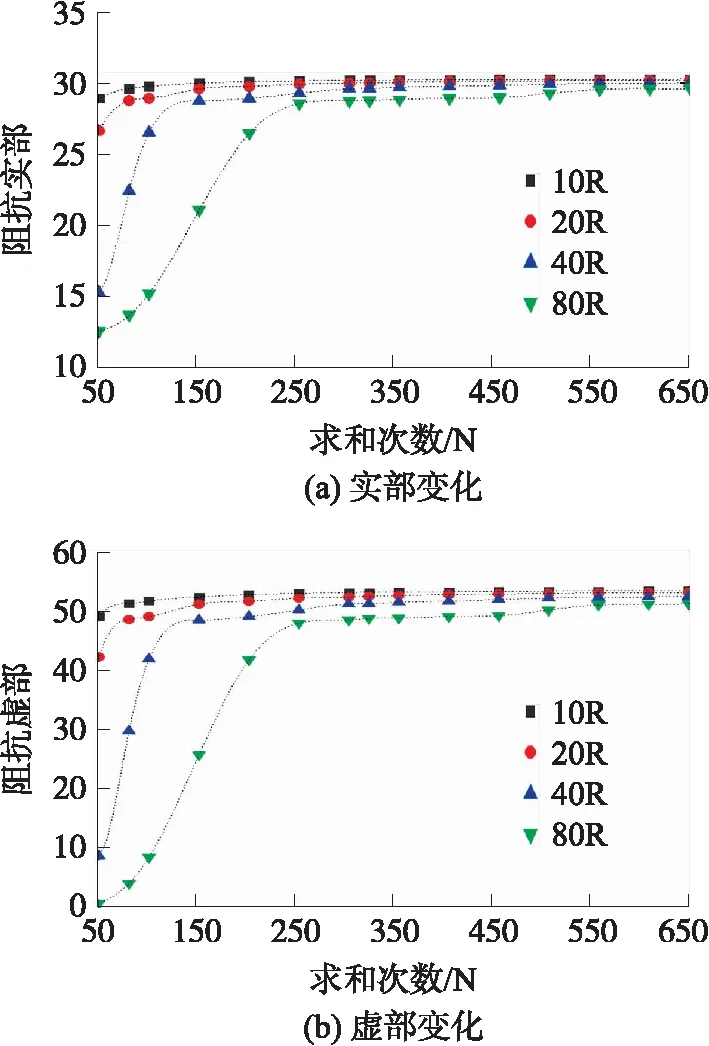
图8 频率为5 MHz时,不同求和次数、不同截断半径的阻抗计算值变化
从得到的计算结果可以看出,在频率为2 MHz、5 MHz下,也存在类似的规律。当截断半径一定时,随着求和次数的增加,其计算结果接近于某一固定值,从而说明这个级数是收敛的。同时通过分析可以得到截断半径越小,收敛的越快。但为了与实际的情况相对应,取截断半径为40R。在保证精度的前提下,为了使计算的效率较高取求和次数为320次。从计算结果可以看出,截断半径和求和次数,不能单独考虑,当截断半径较大时,只有取更大的求和次数,才会更加接近于积分计算的真实值。
3.2 计算与实验结果对比
为了证明计算结果及理论模型的正确性,使用阻抗分析仪对内径为2.25 mm的双层螺旋线圈的阻抗进行测量并对其进行阻抗计算。在0~5 MHz取15个频率点,分别进行测量和计算。结果如图9所示。其中横坐标为频率,纵坐标为阻抗。

图9 线圈内径2.25 mm,阻抗计算与测量结果
从图9可以看出,在频率0~5 MHz计算和测量的阻抗实部、虚部是吻合较好。阻抗实部的最大误差为9.2%,阻抗虚部的最大误差为11.7%。该实验验证了计算的正确性,测量的准确性。
为了验证模型的适用性。又分别对内径1.25 mm、4.25 mm的双层螺旋线圈的阻抗分别进行了计算和测量。结果如图10、图11。

图10 线圈内径1.25 mm,阻抗计算与测量结果

图11 线圈内径4.25 mm,阻抗计算与测量结果
从图10、图11可以看出不同内径的线圈阻抗测量值与计算值在频率5 MHz以下是相吻合的,线圈内径为1.25 mm时,阻抗实部的最大误差为 6.5%,阻抗虚部的最大误差为9%。线圈内径为4.25 mm时,阻抗实部的最大误差为7.8%,阻抗虚部的最大误差为13.4%。比较发现,在高频2 MHz~5 MHz,各个线圈阻抗实部的理论计算结果和测量结果的误差最大为5.3%,各个线圈阻抗虚部的理论计算结果和测量结果的误差最大为7.5%。从而说明了模型的适用性及计算和测量的准确性。
综上,从计算结果和测量结果的对比中可以看出,计算和测量在一定的误差范围内是相吻合的。这说明了计算和测量的准确性,以及模型的适用性。导致计算结果与测量结果之间存在的误差可能是由模型中忽略集肤效应和临近效应引起的。
4 结论
本文通过对双层线圈进行理论建模,推导了双层线圈阻抗计算的级数表达式,并得到了以下结论:
①为了使阻抗计算的精度和计算的效率更高,研究了不同的截断半径和求和次数对计算结果的影响。为了得到最佳参数,从100 kHz、2 MHz、5 MHz 三个频率对其进行计算和分析,得出了随着求和次数增加,计算结果接近于一个稳定的值,计算的精度越来越高。
②通过MathematicTM软件计算求得的线圈阻抗值与测量值的对比分析,证明了理论模型的适用性和编程计算的正确性。
