基于概率向量和机器学习的协作频谱感知*
2020-01-02马永涛王煜东
马永涛,王煜东
(天津大学微电子学院,天津 300072)
近年来,无线通信业务快速增长,造成无线电频谱资源相对匮乏。无线电波非视距传播的特性决定了无线设备适合使用3 GHz以下的频段,频谱固定分配机制虽然在一定历史时期保证了通信系统的稳定性能,同时也造成3 GHz以下的频段被分配殆尽[1]。美国通信联邦委员会(Federal Communications Commission)的研究表明,已授权频谱的频谱利用率只有15%~85%[2]。由于大量授权用户(Primary User,PU)对于授权频段的使用不是连续的,因此在许多时间段上存在大量频谱空穴[3],但是固定的频谱分配政策使未授权用户无法使用这些频谱空穴,造成了授权频段无线电资源的浪费与公共频段的拥挤不堪。认知无线电[4-5](Cognitive Radio,CR)是一种通过使SU利用频谱空穴提高频谱利用率的技术。
频谱感知是认知无线电的核心技术,通过频谱感知,SU能够检测频谱空穴并使用它们,同时也避免对PU产生干扰,是保证高效分配频谱资源的先决条件。初期频谱感知基于单节点[6-7]进行,但由于单节点容易受到阴影、衰落等影响导致感知效果急剧降低,协作频谱感知[7-10]被提出。
在频谱感知中,能量检测[11-14]方法由于复杂度低、检测速度快等优点而受到研究者的青睐。能量检测方法通过实时计算信号能量,与判决门限进行比较,判断PU是否占用通信信道。随着机器学习的兴起,研究者们把机器学习[15-19]应用于频谱感知。文献[15]中,研究者在协作频谱感知中采用了K-Mediods聚类算法,通过详细的数学推理与研究,证明了聚类算法在协作频谱感知中对于抵抗干扰数据的积极作用。文献[16]针对多个PU存在的CRN中的信号检测与识别,研究了基于纠错输出码的多类SVM算法,解决了包含多PU的CRN中频谱感知问题。文献[17]针对低信噪比下频谱感知存在的问题,以信号的协方差矩阵的最大特征值和最小特征值之间的差异作为特征值,采用RBF核函数的SVM算法,提高了频谱感知的性能。文献[18]针对规模较大的CRN,提出了一种基于SVM的协作频谱感知算法,通过对用户分组,有效降低了协作感知的成本。文献[19-20]针对频谱感知中噪声不确定引起感知效果下降的问题,研究了基于模糊支持向量机的协作频谱感知算法。

图1 频谱感知技术分类
本文提出一种适用于机器学习的二维概率向量,通过对能量向量进行数据处理,将其转化为主用户占用频段的概率,降低数据维数以提高在CRN中进行协作频谱感知的效果。本文研究了在K-Mediods与FSVM中分别使用能量向量与概率向量的性能表现。实验结果表明,采用该二维向量,有效降低了机器学习算法中的训练时间与分类延迟。
本文采用能量检测感知信号能量,首先对采样信号x(n)进行模平方得到|x(n)|2,通过求和运算得到信号能量值Y。能量检测流程如图2所示。

图2 能量检测流程图

图3 1个PU与多个SU组成的CRN
1 系统模型及概率向量
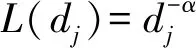
(1)

对于带宽为w的信号,采样频率为fs=2w,能量检测的持续时间为τ,能量检测采样的样本数量为W=fsτ。第j个SU检测到的原始信号能量Yj′(n)为:
(2)
对Yj′(n)进行处理,使:
(3)
式中:η=E[|wj(n)|2]=σ2。由于接收信号yj(n)具有高斯分布,Yj′(n)遵循卡方分布Yj(n)也遵循卡方分布。设在假设H0中Yj(n)的平均值为μYj|H0,则有:
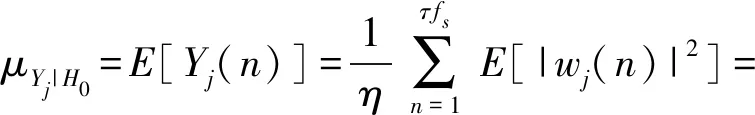
(4)
相应地,由于E[s(n)w(n)]=0,在假设H1中,Yj(n)的平均值为μYj|H1,有:
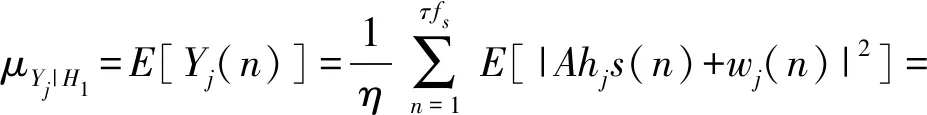
(5)
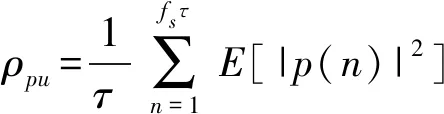

(6)

(7)
当样本数W足够大时,可以认为Yj(n)服从高斯分布。N维能量向量表示为Y=(Y1,…,YN)T,具有多元高斯分布,所以具有以下平均向量和协方差矩阵:
μY|Hi=[μY1|Hi,…,μYN|Hi]T,i=0,1
(8)
(9)


(10)
对于向量Y,在H0和H1假设下,分别有
PHi=φ(Y|μY|Hi,∑Y|Hi)i=0,1
(11)
由于PU不活跃时PH0大于的PH1,PU活跃时PH0小于的PH1,因此可以使用二维向量
P=[PH0,PH1]T
(12)
代替Y=(Y1,…,YN)T进行训练和判断。由于此时P数值很小,对于区分PH0和PH1带来不便不便,因此对其进行变换,有
P[-SlnPH0,-SlnPH1]T
(13)
式中:参数S以及对数函数用于缩放。
2 采用概率向量P的机器学习算法
2.1 K-Meadiods聚类
在“无监督学习”中,通过对无标记的训练样本的学习来获取数据的内在联系及性质,为进一步的数据分析奠定基础。在这种学习中应用最广泛的就是“聚类”。K-Means聚类方法由于其实现算法简洁、聚类效果良好而被广泛应用。K-Means聚类方法虽然实现简洁,在二分类中效果优良,但是由于其算法选择分类中心的机制所限,会显著受到异常数据的干扰,因此本文选择了其改进算法K-Meadiods,一定程度上降低噪声和孤立样本对于分类结果的干扰。

(14)
式中:|Hi|是簇Hi中元素的数量。将P分为两类,则问题转化为:
(15)
(16)
若fc(P)>λ,则认为P属于簇H0,否则属于簇H1,其中λ为算法过程中产生的阈值。
2.2 模糊支持向量机
支持向量机(Support Vector Machine,SVM)是一种建立在统计学理论和结构风险最小原理基础上的模式识别方法,在解决小样本、非线性及高维模式识别中表现出许多特有的优势。其核心思想是利用核函数将低维空间数据映射到高维空间,在高维空间中对数据进行统计分析。模糊支持向量机[20](Fuzzy Support Vector Machine,FSVM)作为SVM的改进,引入了隶属度函数,反映了某个数据对超平面的影响程度,可以降低噪声和孤立样本等异常数据对分类效果的影响。

(17)
式中:slξl是FSVM中带权重的松弛因子。式中C为常数,整体的求解过程和标准的SVM相似,通过构造拉格朗日函数,得到上式的对偶规划为:
yl≥0l=1,2,…,L
(18)
这是一个二次规划(QP)问题。该问题可以进一步优化为:
(19)
按照算法二进行运算,可得到分类函数
(20)
式中:K(x,P(l))=φ(x)·φ(P(l))表示核函数。因此,对于测试概率向量Ptest有:
(21)
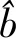


3 仿真与结果分析
3.1 仿真条件与场景
在本节中,对比了使用能量向量与概率向量在不同机器学习算法下的训练持续时间与分类延迟。分别考虑由一个PU和二个SU组成的CRN与由一个PU和16个SU组成的CRN。仿真参数设置如下:带宽w=5 MHz,采样频率fs=10 MHz,感知持续时间τ=100 μs,根据路径损失函数选择信道系数α=4,1≤j≤N,νj和ψj均为1。PU发射功率为100 mW。
3.1.1 由1个PU和2个SU组成的CRN
在这一CRN中,PU与SU的分布如图3所示。其中PU坐标为(1,1)km,2个SU坐标分别为(0.5,0.5)km、(2,2)km。在过去的诸多研究中,这种基本情况被广泛用以形象化地解释所提出的算法,本文同样首先以此CRN作为基础展开研究。
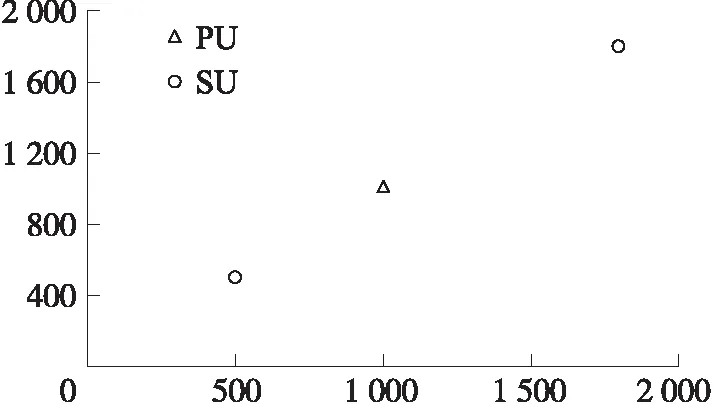
图4 1个PU与2个SU分布
表1列出了在具有1个PU和2个SU的CRN中,两种算法分别采用能量向量与概率向量的训练时间。可以看到,随着训练样本的增加,训练时间也合理地延长。对于同一种算法,采用能量向量与概率向量在这一CRN中的训练时间非常接近,没有明显差别,因为能量向量与概率向量都是二维向量。而对于不同算法,明显可以看到采用FSVM的时间比K-Mediods大为减少,表明连续聚类比求解凸优化问题耗费更多时间。

表1 训练持续时间(N=2) 单位:ms
表2列出了两种算法的分类延迟。根据式(16),K-Mediods分类时间主要取决于测试向量的维度,而不是样本数量,且质心的计算完成与训练阶段,也不会占用分类时间,因此其分类延迟不受样本数量的影响。显然,对于能量向量与概率向量,K-Mediods的分类延迟相同。根据式(20),FSVM的分类延迟不仅受到被分类向量维数的影响,还会受到支持向量数量的影响,而随着样本数量的增加,支持向量数量也会增加,因此分类延迟也增加。而对于能量向量和概率向量,与K-Mediods 类似,分类延迟非常接近,并无明显的差别。

表2 分类延迟(N=2) 单位:ms

图5 检测概率与SU个数/PU个数关系(虚警率Pf=0.1)
3.1.2 由1个PU和16个SU组成的CRN
由图5可以发现,当只有1个PU时,SU数量由9个增加到16个时,检测概率没有发生相当明显的变化,因此本文考虑由1个PU和16个SU的CRN,布局如图6所示,它们均位于2 km×2 km的正方形中。其中PU在(0.5,0.5)km处,SU均匀分布在正方形中,坐标如图6所示。
表3列出了在具有1个PU与16个SU的较大规模的CRN中,两种算法分别采用能量向量与概率向量的训练时间。与表1相同,随着训练样本的增加,训练时间也合理地延长。与表1不同的是,对于同一种算法,采用能量向量与概率向量的训练持续时间随着样本数量的增加幅度产生较大的差别。这是因为概率向量是2维向量,对于训练时间表现出稳定性。当然,在16维能量向量转换为2维概率向量的过程中不可避免牺牲了一定的时间,因此对于同一种算法,采用概率向量比表1中的时间略有增加。但是这种增加远低于采用能量向量所导致的训练时间的巨额提升。

图6 1个PU与16个SU分布
表4列出了两种算法分别采用能量向量与概率向量的分类延迟。基于式(15),采用16维能量向量时K-Mediods的分类延迟比表2中增加了许多,但是没有受到样本数目增加的影响。采用概率向量的分类延迟与表2中非常接近。类似地,对于FSVM,采用概率向量比采用能量向量有更低的分类延迟。

表4 分类延迟(N=16) 单位:ms
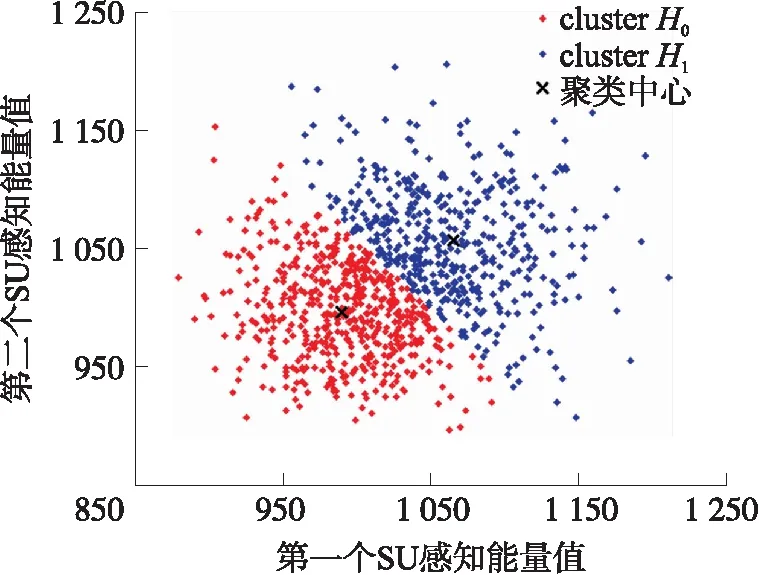
图7 基于能量向量的K-Mediods分类
3.2 仿真结果
仿真结果如图7~图12所示。

图11 不同算法基于能量向量和概率向量的ROC曲线(16SU,-12 dB)

图8 基于概率向量的K-Mediods分类

图9 基于能量向量的FSVM分类

图10 基于概率向量的FSVM分类
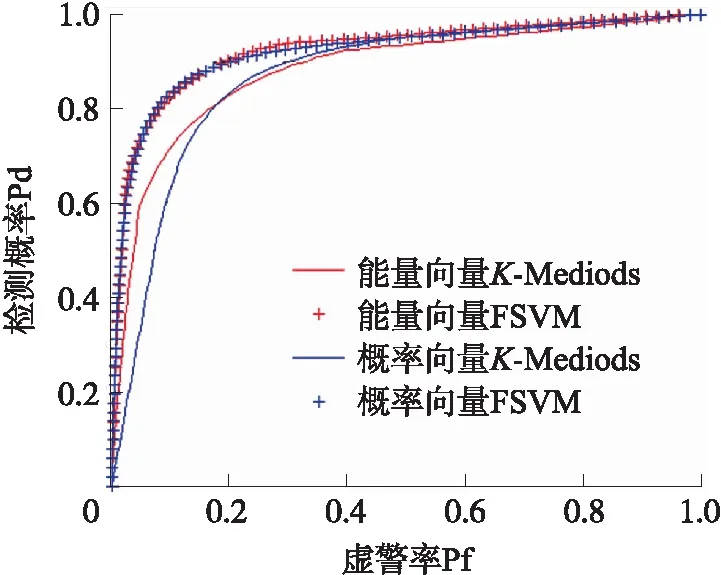
图12 不同算法基于能量向量和概率向量的ROC曲线(16SU,-8 dB)
3.3 仿真结果分析
图7~图10分别展示了在图4分布下观测到的能量值和相应的概率向量及分类。图7采用K-Mediods 聚类方法对能量向量进行了分类,分类中心如图中黑色X标记所示。水平坐标轴与竖直坐标轴分别代表一个SU感知得到的能量数值。明显看到,对于两条坐标轴数值都偏低的节点,分类器将其判断为H0,意味着这些节点中不存在PU用户;相反,对于两条坐标轴数值都偏高的节点,分类器将其判断为H1,这也符合我们的预期,即信道中存在PU信号时能量普遍大于只存在噪声的情况。图8,将概率向量应用于K-Mediods聚类,可以看到其数据形成了弧形,且在弧顶聚集了大量数据。同样地,黑色X标记代表了分类中心。此外,图7与图8的坐标数值也有着巨大的差异,这是由于在能量向量变换为概率向量的过程中进行了复杂的数学运算。虽然数值有了较大的改变,但是两图中数据对应的意义仍然一致。图9 与图10分别表示使采用能量向量与概率向量的FSVM算法。与图7不同,图9中分类的依据不是某一个中心点,而是由数量庞大的绿色支持向量作为分类的依据,其带来的影响之一就是分类精度的提高,但也会导致分类延迟随着样本数量的增加而增加,表2 和表4的数据都支持这一判断。对于图6中的场景分布,无法直观地画出能量向量的分布图,因此为了更好地对比两种算法,采用ROC曲线来比较两算法的性能。图11表示由1个PU与16个SU组成的CRN在-12 dB时的ROC曲线。显然,对于同一种算法,两种向量所对应的曲线性能极为接近,在虚警率较低时,采用概率向量所对应的检测概率比采用能量向量所对应的检测概率略低一些,而随着虚警率提升,两类曲线逐渐趋于吻合,ROC曲线的非常接近。图12表示由1个PU与16个SU组成的CRN在-8 dB时的ROC曲线。通过观察可以发现,对于FSVM算法,采用能量向量与概率向量的两条ROC曲线吻合度非常高,在虚警率小于0.2的范围内,两条曲线近似重合;对于K-Mediods算法,在虚警率小于0.2时采用能量向量时的检测概率比采用概率向量时的检测概率略高一些,但是当虚警率提升到0.2后,后者的检测概率反而比前者更高一些,显然,在这一情况下ROC曲线的性能有了略微的提高。
4 结语
本文提出的二维概率向量,适用于在SU较多的CRN中进行协作频谱感知,通过能量检测获取各个SU采集到的能量值,组成高维向量,对此向量进行数据处理,有效降低了数据维数。并且在采用机器学习算法进行验证后,发现其比能量向量在训练时间、分类延迟中都具有更加优良的性能表现,而通过ROC曲线可以发现其性能损失很小,甚至在某些情况下会展现出更好的性能表现。
