木星系探测中多层材料的辐射屏蔽优化设计方法

王建昭，马继楠，张庆祥，李衍存，贾晓宇，田 岱，朱安文，邱家稳

（北京空间飞行器总体设计部，北京100094）

0 引言

近年来，木星探测逐渐成为深空探测的焦点和热点之一。随着Galileo号和Juno号任务的成功实施，人类对木星这一巨行星的了解大大增加，包括动态大气、强引力场、内部结构、巨大磁层及木星卫星等。另外，NASA 和ESA 将分别于2021年和2022年发射Europa Clipper[1]和JUICE[2]探测器，用以研究木卫二和木卫三的宜居性。

与其他深空探测任务相比，木星探测的难点在于其恶劣的辐射环境[3]。木星磁场比地球磁场强20倍，因此可捕获大量高能带电粒子。一般而言，在木星系中，质子和电子的最高能量可达1 GeV。木卫二轨道的高能粒子通量比地球GEO的大1～2个数量级[4]。另外，与地球辐射带相比，木星辐射带中的高能粒子数量更多、能谱更硬[5]。其次，木星系中带电粒子通量的不确定性大，同一位置的粒子通量最高比最低时大4倍，且这种不确定性随着距木星中心距离的增大而增加[6]。

在木星辐射防护设计中，对高能粒子引起的电离总剂量效应的防护是主要难点[7-8]，也是木星任务设计中的重点。除常用的整星质量屏蔽，还需对辐射敏感器件进行额外的防护，将敏感器件安装在屏蔽盒内。在Galileo号的设计中，重点元器件利用厚度为1 cm 的钽盒进行防护[9]。在Juno号的设计中，采用了厚度为1 cm 的钛材料矩形屏蔽盒[10]，其重量达到180 kg。可见，木星探测中辐射防护的代价巨大，如果能对屏蔽结构进行优化，在较低的代价下获得相同的防护效果，将大大节省航天器重量资源，这对深空探测十分重要。

在不损失结构强度、导电性能等的前提下，同等面密度下多层屏蔽材料的防护性能优于单一铝材料[11]。因此，可采用多层屏蔽的设计方法，且将高原子序数（高Z）材料（钽、钨、钛等）和低原子序数（低Z）材料结合，达到屏蔽效果优化的目的。Cherng 等[12]的研究结果表明，当面密度大于10 g/cm2时，铝/钨多层屏蔽效果好于单层铝屏蔽。Fan 等[13]的研究结果表明，对于地球MEO 的电子辐射环境，相同面密度下，铝/钽/铝的多层结构比单层铝结构的屏蔽效果高60%。另外，外部辐射环境、多层结构中不同材料的含量[14]、不同屏蔽层的叠放顺序[15]、屏蔽层的数量[16]等众多因素都会对多层屏蔽效果产生影响，难以通过解析算法得到最优的多层屏蔽结构。

本文试图利用遗传算法，针对具体的木星任务，得到最优的多层屏蔽结构，为我国未来木星任务的辐射防护设计提供参考。

1 木星系辐射环境及防护特性

1.1 木星系辐射环境

本文利用JOSE 模型[17]计算木星辐射带中的高能粒子辐射。考虑到未来木星任务主要探测目标为伽利略卫星，选择的轨道需覆盖木卫二（9.5RJ，RJ=71 492 km 为木星半径）至木卫四（25RJ），因此选择近木点和远木点分别为10RJ和25RJ的赤道面轨道。该轨道平均微分能谱如图1所示。在木星系中，辐射环境以高能电子为主，电子通量比质子通量大1～2个数量级。

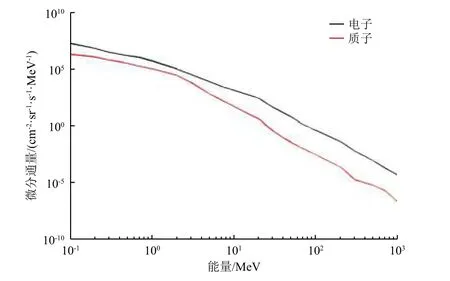
图1 木星探测轨道（10R J×25R J×0°）微分能谱Fig.1 The differential electron and proton spectra in Jovian orbit (10R J×25R J×0°)

1.2 质子与电子的辐射防护特性

高能粒子与物质相互作用，经过复杂的物理过程导致能量损失并产生次级粒子。对于质子，其产生的次级粒子可忽略，能量损失以非弹性散射为主。对于非弹性散射，质子能量损失过程中角度变化不大，因此其在物质中的传输路径基本符合前向近似。非弹性散射过程中物质的阻止本领与Z/A比值正相关，其中Z和A分别为物质的原子序数和质量数。除了氢元素，总体而言，随着Z的增加，不同元素的Z/A值逐步减低，因此低Z材料更有利于质子的辐射屏蔽防护。

对于高能电子，其与物质相互作用包括弹性散射、非弹性散射及轫致辐射。对于非弹性散射，与质子相似，低Z材料更有利于电子非弹性散射的屏蔽防护。对于弹性散射，电子能量损失不显著，但方向会发生显著偏离，因此在输运过程中电子的角度散射明显，不符合前向近似。弹性散射过程中物质的阻止本领与Z2/A比值正相关，因此高Z材料更有利于电子弹性散射的屏蔽防护。另外，当电子能量大于1 MeV 时，发生轫致辐射而产生光子的物理过程较为重要。轫致辐射的产生亦与屏蔽材料的Z2/A比值正相关，因此高Z材料产生的轫致辐射更多，不利于对电子轫致辐射的防护。而轫致辐射产生的光子又可以与物质继续作用，产生光电效应、康普顿散射、正负电子对等，这些物理过程中光子能量损失与屏蔽材料的Z值正相关，因此高Z材料有利于光子的屏蔽防护。总而言之，对于电子防护，高Z材料有利于弹性散射和光子的防护，而不利于非弹性散射和韧致辐射的防护。

综上，高Z和低Z材料对于电子和质子的防护影响制约条件很多且规律不同，仅利用物理规律对多层屏蔽材料的种类、厚度、叠放顺序等进行选择存在一定困难，需借助智能算法进行优化求解。

2 优化分析方法

航天器常用多层材料进行辐射防护，而防护效率依赖于多层的材料、厚度、叠放顺序等众多因素，因此多层屏蔽防护设计是典型的优化问题，可用遗传算法选择最优的屏蔽结构，并利用MULASSIS（Multi-Layered Shielding Simulation Software）程序[18]进行屏蔽效率评估。MULASSIS是基于Geant4开发的粒子输运一维仿真程序，其原理是利用Monte Carlo方法，模拟多个粒子在多层材料中的输运过程，记录粒子位置、能量损失、次级粒子等信息，从而达到分析屏蔽效果的目的。利用遗传算法进行优化时，具体可有多种优化目标，例如：在特定剂量指标下寻找最低质量的多层屏蔽方案；在给定质量限制后寻找最优屏蔽方案使屏蔽后的剂量最小等。

2.1 分析流程

遗传算法求解流程如图2所示。在第1代，随机生成由m个个体组成的族群，每个个体由1组二进制数组表示，代表一种可能的多层屏蔽方案，包含屏蔽材料、屏蔽层数、每层厚度、叠放顺序等信息；利用MULASSIS程序计算在木星环境下经每种方案设计屏蔽后的剂量，以目标函数为判据得到每个个体（屏蔽方案）的适应度；如果存在最优个体满足设计要求，则终止优化过程，否则继续创建下一代族群。在每一代中，父代通过杂交和变异产生m个新个体（后代），这些新个体和父代一起组成了下一代族群候选个体（共2m个），再通过目标函数选择最优的m个个体组成下一代族群。

图2 遗传算法求解流程Fig.2 Flowchart of genetic algorithm

2.2 编码方法

在遗传算法中，需将每个个体进行编码，即产生染色体。编码需包含材料类型、厚度、叠放顺序等信息。本文共设定8种可选材料，其属性如表1所示。

表1 不同屏蔽材料属性Table 1 The properties of different shielding materials

默认屏蔽层数为n层，用10n位的二进制编码表示每个个体的染色体，每10位二进制数表示1层的信息，即1个基因，编码的顺序则为各层的叠放顺序。在每一层中，前3位表示所选的材料类型，根据原子序数从小到大排列，如{0,0,0}代表镁层，{1,1,1}代表铅层；后7位表示每层厚度ti，mm。根据文献[19]，

式中：vk为对应基因上相应位的二进制值；N=7，则7位数可表示0.01 mm 至1 mm 的27个不同厚度值。例如：{1,0,1,0,1,0,1}表示的厚度为0.673 mm。

2.3 目标函数

本文讨论的优化目标为：在给定质量上限时，寻找最优屏蔽方案使屏蔽后的剂量最小。因此目标函数为

其中：f(x)为目标函数；x为族群中的个体；D为经MULASSIS程序仿真得到的经对应方案屏蔽后的剂量；S为决策空间。在仿真中，依次读取10n个二进制数，若读至第n1（n1＜n）层时前n1层的质量已超过设定的质量上限，则不再继续读取，仅取前n1-1层为屏蔽结构；另外，如果连续数个屏蔽层的材料相同，则认为是同一层，厚度为这几层的厚度之和。利用MULASSIS程序进行仿真时，每次仿真计算105个粒子入射屏蔽层后在0.1 mm 硅探测器上的能量沉积。

在MULASSIS 程序中，为模拟真实空间各向同性的粒子源，常采用平面粒子源且粒子通量呈cosθ型分布，θ为粒子方向与平面源法向的夹角。这是因为，对于面源，沿θ角度发射的粒子通量是沿法向发射的粒子通量的cosθ倍，而接收平面所接收的通量不随θ而变，可达到构建各向同性辐射环境的目的。仿真中，需设置归一化参数，使仿真的粒子数转化为真实空间中的通量。假设空间各向同性通量微分能谱为Φ(E)，则归一化参数为

2.4 杂交与变异

在当前族群中，所有个体随机组合形成m/2个父代对（用πi和πj表示），每对个体产生2个后代（用π’i和π’j表示）。每个个体包含10n个染色体，即n个基因，父代的每个基因按顺序随机分配到子代，对于相同位置的基因，2个子代个体分别随机继承于2个父代，如图3所示。

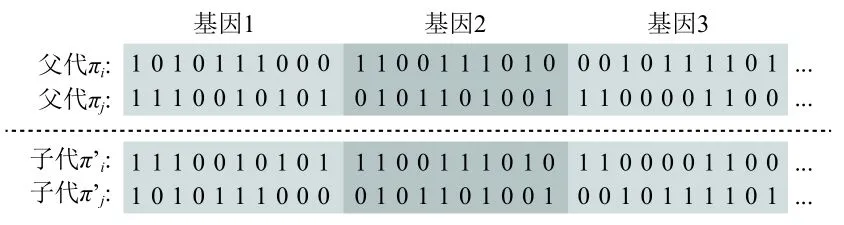
图3 遗传算法中的杂交过程Fig.3 The crossover processin genetic algorithm

在生成的个体中，每个个体都有一定概率发生变异。假设变异概率为r，则对于子代个体的染色体中的每位二进制数，都有r的概率由0变为1或由1变为0。

3 结果

3.1 防护最优的多层屏蔽结构

在本算例中，设屏蔽面密度阈值为1 g/cm2，单个族群包含20个个体，屏蔽结构最多包括10层，即n=10。设每个染色体编码位的变异概率r为0.1，将优化过程进行40代得到最优的屏蔽结构。优化过程中的每代最优个体的目标函数（即屏蔽后剂量）如图4所示。

图4 最优结构的屏蔽后剂量随算法代数的变化Fig.4 The dose after best shielding structure vs.generation number of genetic algorithm

对于随机产生的第1代族群，经每个个体对应的屏蔽结构防护后，辐射总剂量的平均数值为728.6 krad(Si)/a，其中最优个体对应的屏蔽层防护后总剂量为128.9 krad(Si)/a。随着代数的不断增加，每代中的最优个体（屏蔽结构）不断被优化，最终得到的最优结构采用0.829 mm 铅（Z最大）和0.158 mm 镁（Z最小）的组合，结合了高Z材料及低Z材料，总面密度为0.97 g/cm2。遗传算法收敛速度较快，在较小的计算代价下即可寻找到最优解。

利用MULASSIS程序进行仿真，该屏蔽方案可将图1所示的木星轨道辐射环境造成的辐射总剂 量 降 低 至120.3 krad(Si)/a。对 于 单 层 钽（如Galileo号）、钛（如Juno号）、铝3种材料，若要达到与其相同的屏蔽效果，所需的面密度分别为1.17 g/cm2、1.71 g/cm2、1.72 g/cm2。可见，相对于单层钽、钛、铝屏蔽，该屏蔽结构可节省的重量资源比例分别为17.1%、43.3%、43.6%，表明利用本优化算法得到的屏蔽结构设计方案，可大大节省未来木星探测器所需的屏蔽质量。

3.2 不同质量限制下的最优结构

计算不同面密度限制下的最优屏蔽结构，并仿真得到它们将图1所示的木星轨道辐射环境造成的辐射总剂量屏蔽后的结果，如表2所示。

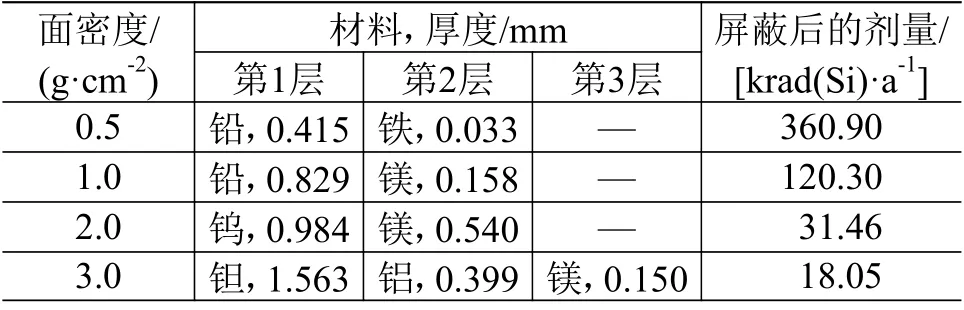
表2 不同面密度限制下的最优屏蔽结构Table 2 The best shielding structures under different areal density constrains

可以看出，对于不同的质量（面密度）限制，一般而言，利用遗传算法进行优化得到的最优屏蔽结构有3个特点：

1）将高Z材料与低Z材料相结合，更有利于木星辐射带的辐射防护。

2）多为2层或3层结构。这可能是由于存在剂量增强现象[20]。剂量增强是指，在高Z材料中高能电子与材料相互作用产生轫致辐射，轫致辐射产生的光子在高Z和低Z材料界面发生背散射并产生低能的二次电子，这些电子将贡献额外的剂量。一般而言，层数越多剂量增强现象越显著，故最佳屏蔽结构的层数不宜过多。

3）采用高Z材料在外、低Z材料在内的叠放顺序。这可能是因为相对于低Z材料，高Z材料背反射系数更大，可以将更多高能粒子反射回空间中。根据文献[7]，对于1 MeV 电子，垂直入射情况下铝（Z=13）材料的背散射系数为12%，钽（Z=73）材料的背散射系数为48%，将钽材料置于外侧更有利于辐射防护。

4 结束语

在木星系探测中，高能粒子的辐射防护是关系到任务成败的关键。在航天器设计中，常用多层金属材料屏蔽高能粒子辐射。本文结合MULASSIS多层屏蔽评估程序，提出了基于遗传算法的优化方法，在限制总屏蔽质量的前提下得到最优的多层屏蔽结构，高能粒子经过该结构的屏蔽后产生的电离总剂量最低。优化结果表明，对于10RJ×25RJ×0°的木星探测轨道，若屏蔽层的总面密度限制在1 g/cm2以下，最优的屏蔽方案是将铅和镁相结合，可将电离总剂量降低至120.3 krad(Si)/a，与传统铝屏蔽材料相比，相同屏蔽效果下可节省近43.6%的重量资源。另外，对于不同的面密度要求，一般而言，最优屏蔽结构都是将高Z材料与低Z材料相结合，且多为2层结构或3层结构，并把高Z材料放置在外侧。

利用遗传算法对多层屏蔽材料结构进行优化，存在显著优势。首先，该算法不对材料种类和层数进行先验选择，而是在众多可能的结构中自动进行优化得到最优结构，可实现潜在方案的全覆盖。另外，该优化方法可与轨道设计相结合，针对特定轨道进行精细化的屏蔽结构设计，并在任务全周期进行迭代设计。然而，该方法得到的最优结构仅是理论值，未考虑工程可实现性：一种多层结构要想用于航天器的设计，还需满足机械、热控、电子等分系统的其他要求，并对潜在的多层屏蔽设计方案进行多种试验验证。

另外，目前的优化算法只考虑了电离总剂量，最优的结构使屏蔽后的总剂量最小。可通过改变目标函数，增加其他优化要素，如：非电离能损、造价等因素，从而形成多目标的多层屏蔽优化设计方案。