爆炸地震波作用下埋地管道流固耦合动力响应研究
2020-01-01丁宇奇1戴子威1烨1明1强1李为卫马秋荣
丁宇奇1,戴子威1,芦 烨1,杨 明1,张 强1,李为卫,马秋荣
(1.东北石油大学 机械科学与工程学院,黑龙江大庆 163318;2.石油管材及装备材料服役行为与结构安全国家重点实验室,西安 710077)
0 引言
埋地管道作为一种高效的油气运输方式具有运量大、占地少等优点,在世界范围内得到广泛应用[1-3]。随着国内基础设施建设规模和地域的扩大,管网场地爆破施工变得更加频繁,由此引发的土体振动常常导致埋地管道的外爆破坏,因此,探讨埋地管道在外爆振动载荷作用下的结构响应问题,对预防和控制此类事故具有重要的意义[4-7]。
埋地管道在外爆振动载荷下的破坏,主要与爆炸所产生的振动,即爆炸地震波、管土相互作用和管内输送介质有关[8]。针对外爆载荷对空管的作用问题,都的箭等[9]通过试验方法得到了管道响应与爆心距的关系,同时验证了数值模拟方法能够很好地模拟炸药爆炸过程;张震等[10]通过试验和数值模拟相结合的方法,得到了管道拉应力峰值与振速峰值的关系;徐国富等[11]用试验研究了空中爆炸冲击对埋地管道的动力响应;谌贵宇等[12]利用数值模拟,解决了炸药库意外爆炸后的地震波影响下不同工况的管道振速及相应的安全距离。在管土相互作用问题上,纪冲等[13]用无拉力土弹簧描述管土间作用,并研究模型在外爆载荷下的动力响应;杨辉等[14]给出了管土相互作用的弹性解析解,并用数值模拟加以验证,得出了管土接触分析能够较好地模拟管土作用的结论。在管内介质问题上,徐英儒[15]通过数值模拟方法,对比分析了爆炸作用下输气管道和输液管道的应力、位移、速度和加速度响应时程;刘学通[16]将管内流体简化为内压,进行了管道响应数值模拟分析;赵广宇[17]考虑了含液管道在自然地震波作用下的动力响应问题。
综上所述,现有研究主要是将管内流体对管道的作用效果等效为内压载荷,而实际外爆振动对管道的破坏,与管道内流体流动状态密切相关。为此,本文通过建立土体-管道-管内流体的流固耦合动力学模型,对埋地管道在外爆地震波作用下的响应进行分析,通过分析管内流体不同输送压力与流体流速对管道振动的影响,探讨不同影响因素下埋地管道外爆振动响应。
1 埋地管道外爆流固耦合动力模型的建立
1.1 几何模型和有限元计算模型
埋地炸药爆炸之后气体向外膨胀冲击土体,在土体中传播冲击波并使爆心附近(一般认为10~15倍装药半径范围内)的土体压碎、破裂,同时其波速、压力、能量随着距离的增加而很快衰减,此时冲击波传播区域为“爆炸近区”;在离开爆心10~15倍装药半径后,岩体中冲击波的能量衰减到某一临界值时,冲击波开始转换为没有陡峭波阵面的应力波(弹塑性波),该区域称为“爆炸中区”(小于400倍装药半径);而后非弹性过程逐渐终止,显示出弹性效应,并以地震波的形式向外传播,此区域称为“爆炸远区”(400~500倍装药半径)[18-19]。本文选取TNT炸药为边长0.2 m的立方体,装药半径0.1 m,为使爆炸载荷主要以地震波形式作用于管道,设置管道外表面与TNT炸药中心距离为40 m,炸药起爆点设置在炸药中心。实际情况下埋地管道长度大,但由于爆心距较大,且爆炸载荷作用于管道的范围有限,为缩小模型尺寸,将埋地管道长度设为2 m;根据真实管道尺寸,取管外径813 mm,管壁厚度9.5 mm,管道埋深1 m;管道两侧处理为自由边界,以消除管道长度带来的边界效应,管道与土体之间为接触作用,整体几何模型如图1所示。

图1 埋地管道外爆几何模型示意
管道采用壳单元,土体、炸药、流体采用实体单元进行离散,管道与土体采用拉格朗日网格描述,炸药和流体采用欧拉网格描述;土体除上表面为自由边界外,其他面均施加无反射边界条件,其目的是为了消除爆炸波在边界处的反射;爆炸地震波传播方向指向管道,在管道中间截面取迎爆点A和背爆点B两点作为管道径向位移与应力响应的监测点,模型整体施加重力,有限元模型如图2所示。

图2 有限元模型示意
外爆炸药采用TNT高能炸药材料模型[20],并采用JWL状态方程来描述炸药爆炸过程,其状态方程表达式为:
(1)
式中P——TNT爆炸压力,Pa;
A1,B1,R1,R2,ω——TNT材料常数;
η——相对体积,量纲为1;
e——自然对数;
E0——TNT初始比内能,J/m3。
管道材料本构方程采用随动硬化双线性弹塑模型,遵循von Mises屈服准则,其表达式为:
(2)
式中σ——管道应力,Pa;
Es——管道弹性模量,Pa;
σy——管道屈服强度,Pa;
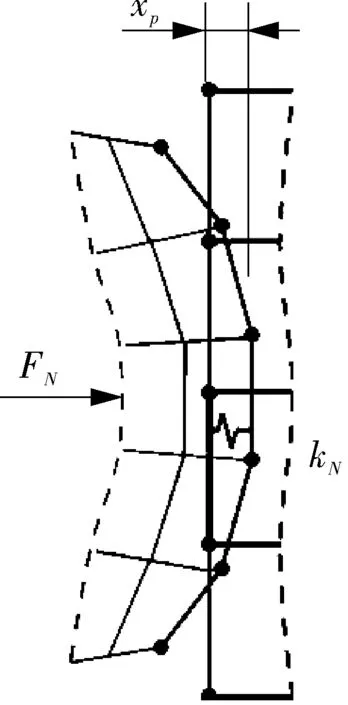
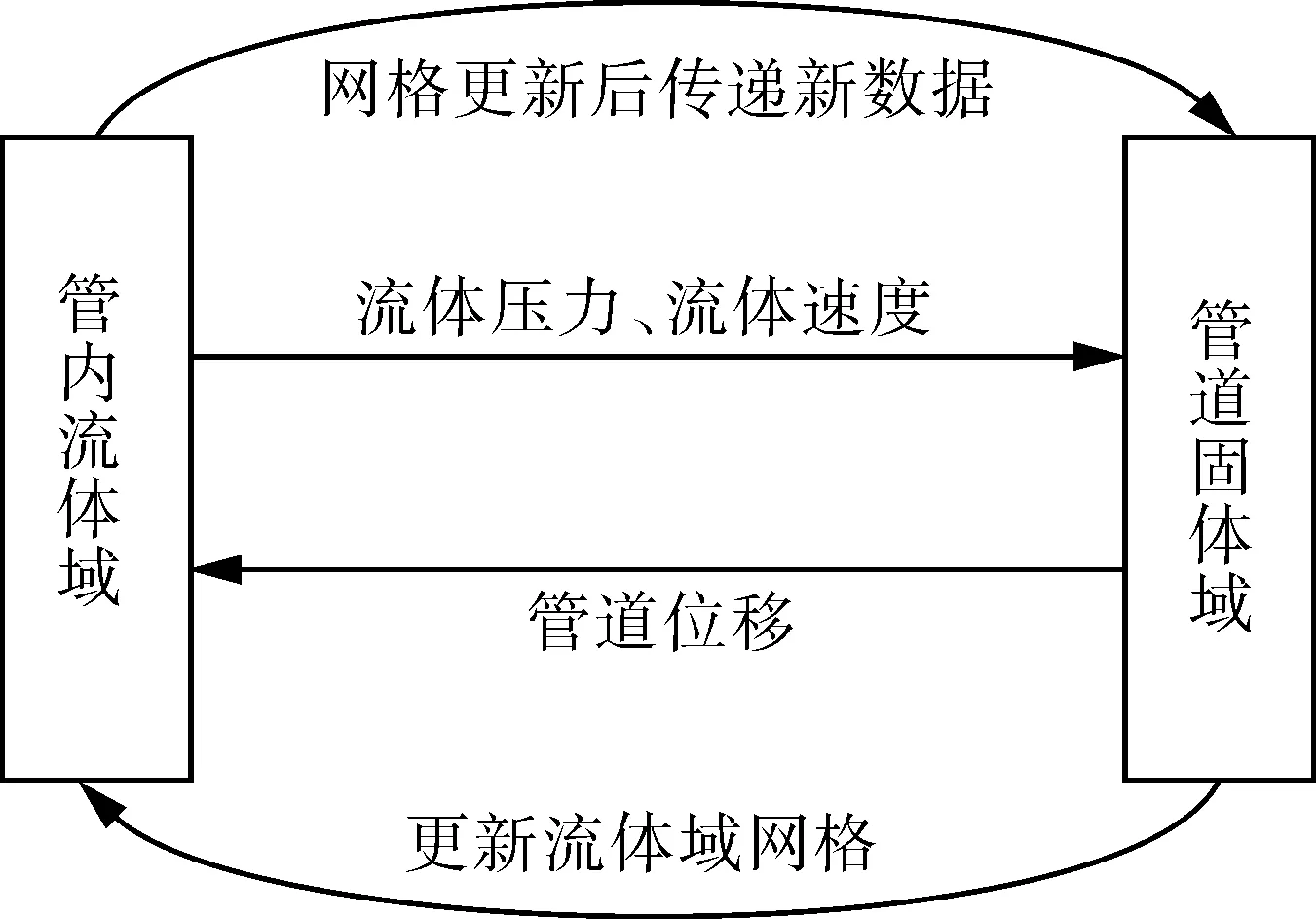
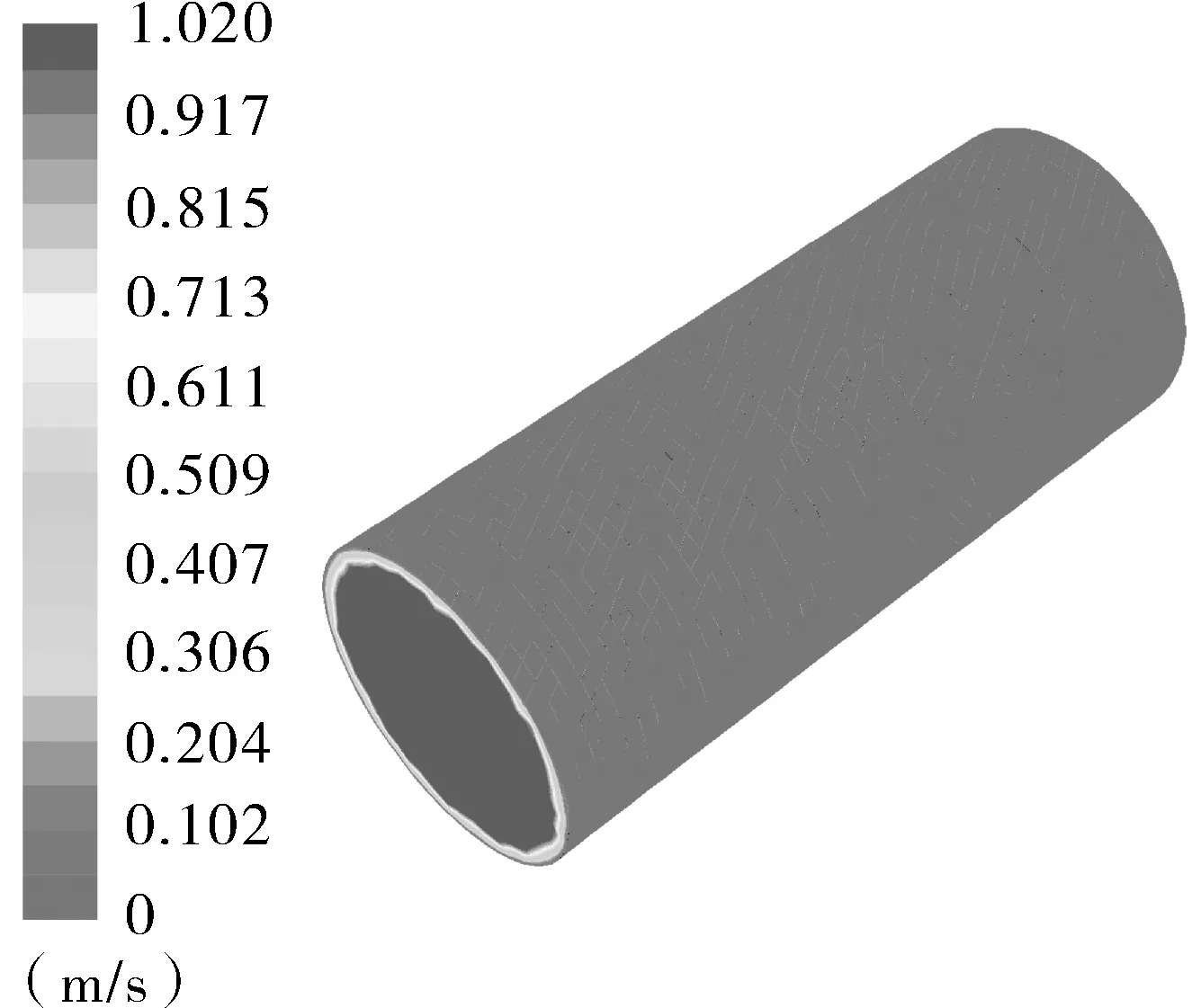
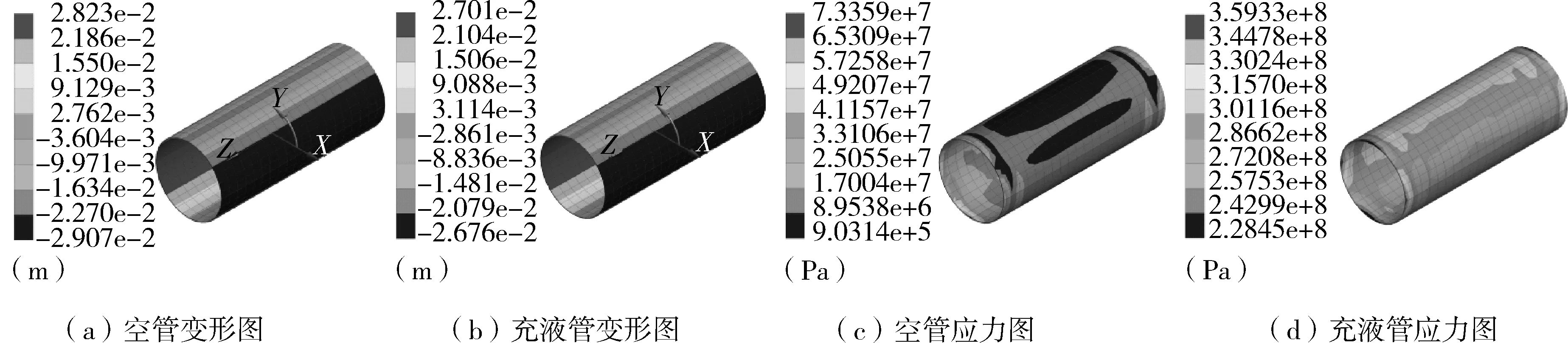
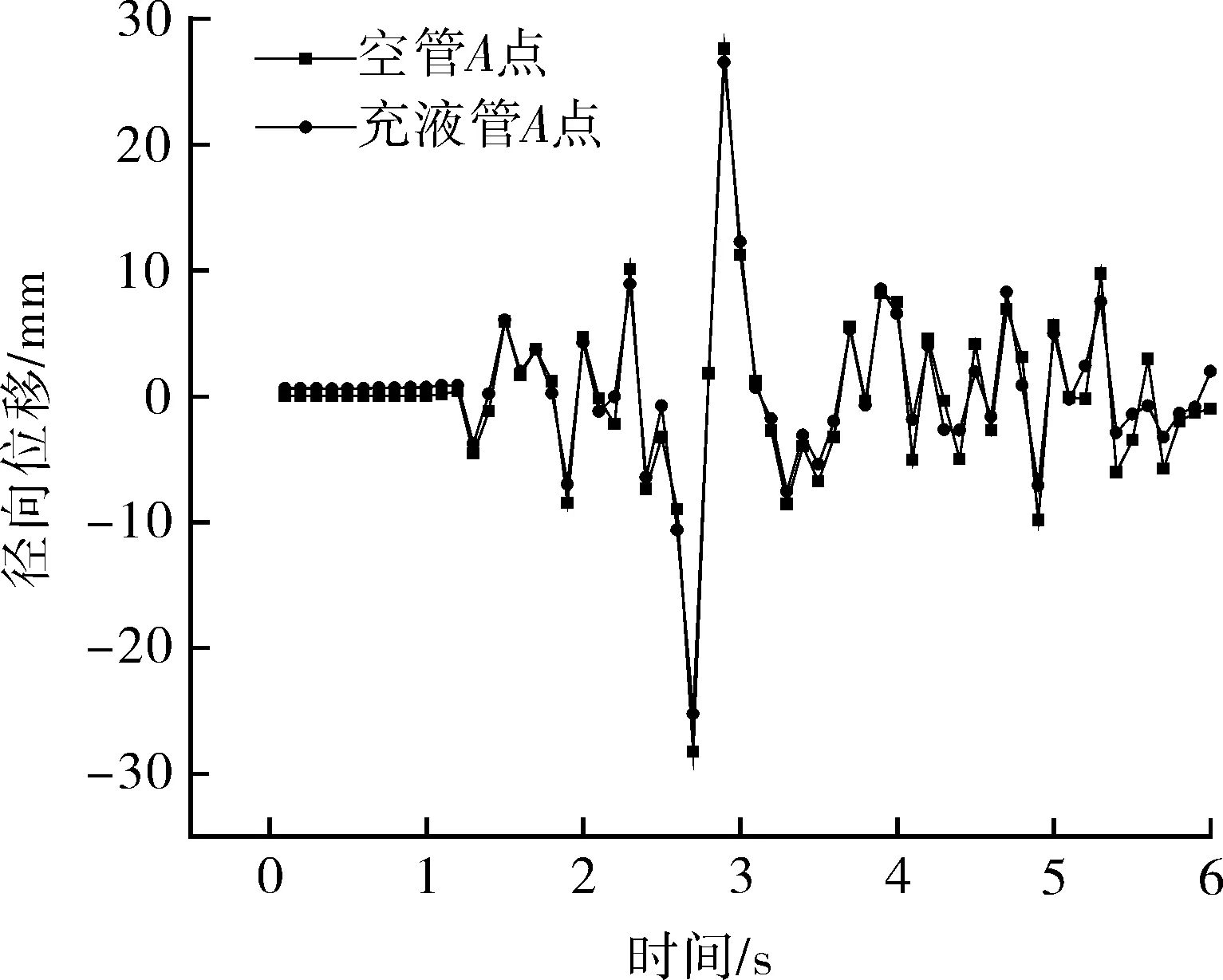
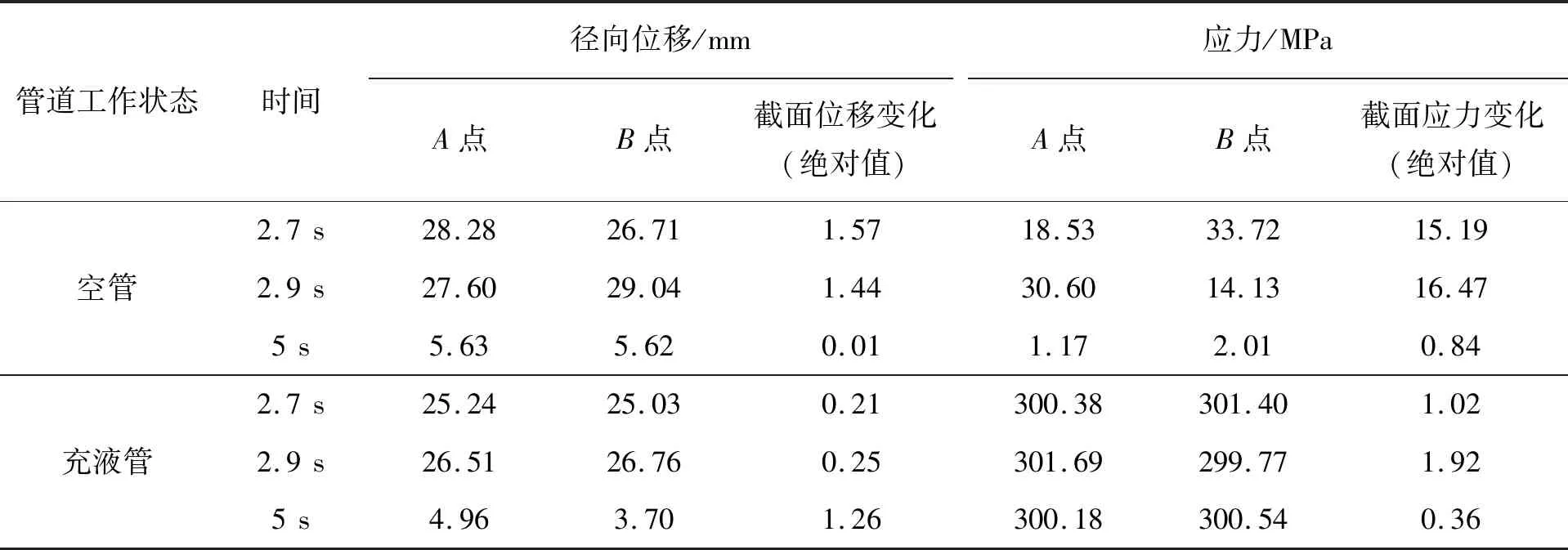
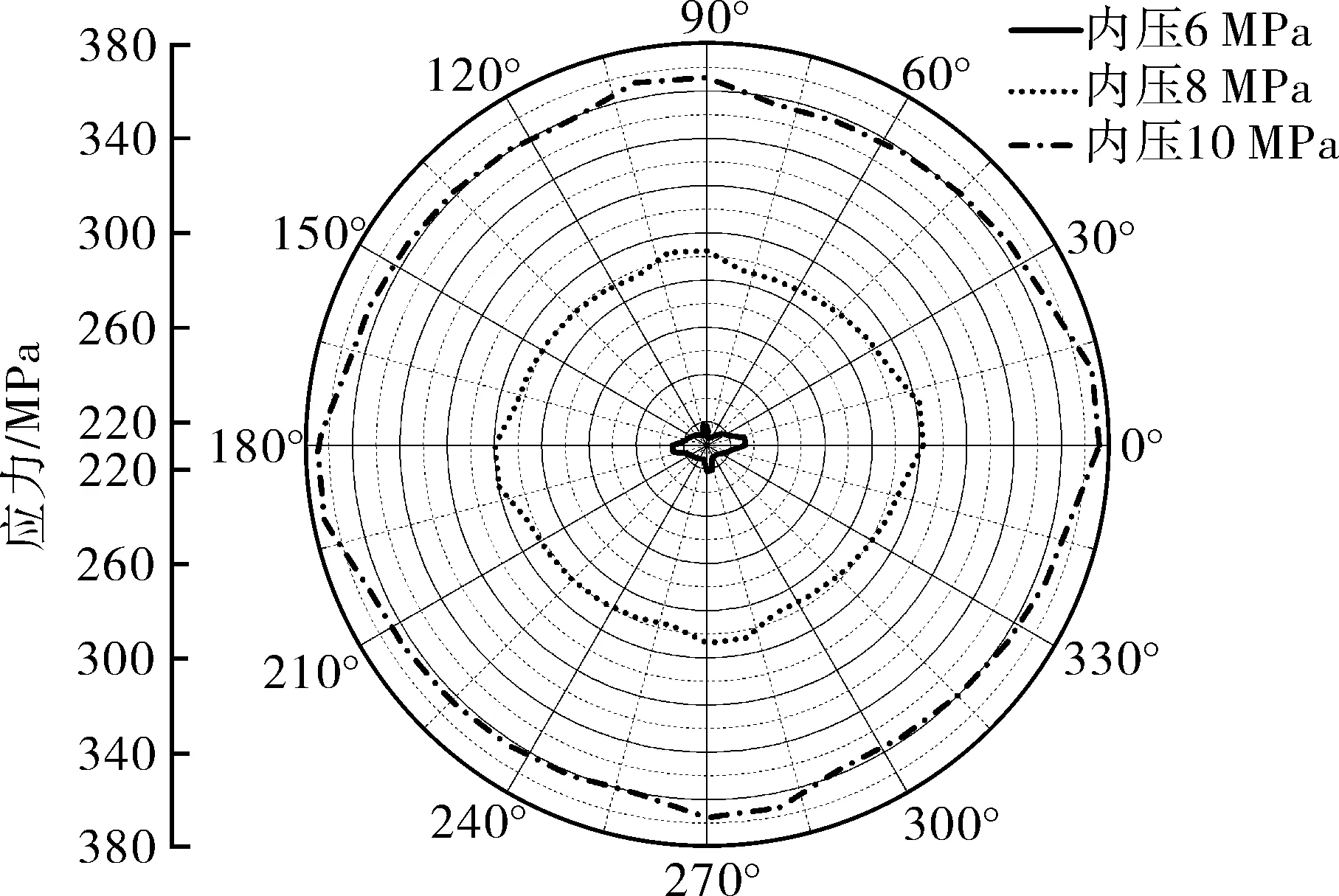
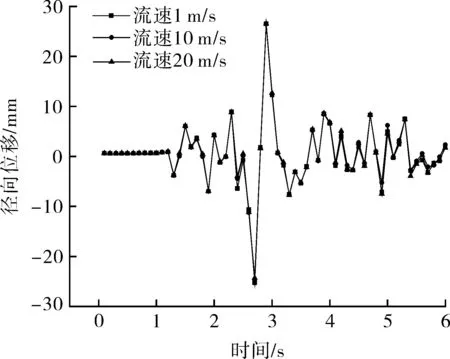
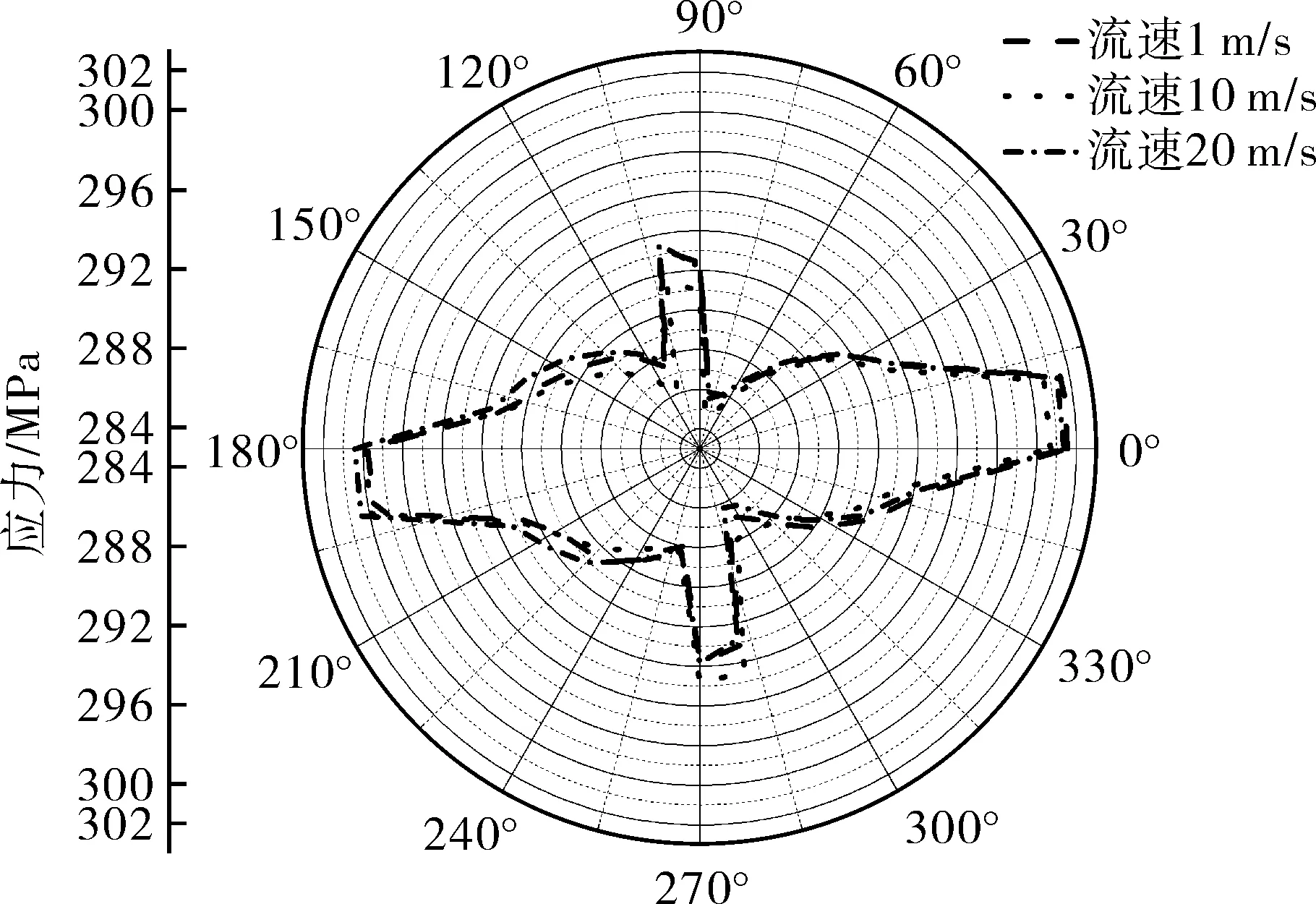
Et——管道切线模量,Pa,且0 εe——弹性极限应变。 管道材料选用X70钢的参数。土体材料采用Drucker-Prager材料模型,该模型可有效模拟土壤,它考虑了材料的剪切膨胀特性,允许材料各向同时硬化或软化,并可以描述土壤的长期塑性变形。表1列出土体材料参数。 表1 土体材料参数 管内流体采用多状态线性方程描述: P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ +C6μ2)E0 (3) 式中P——流体压力,Pa; C0~C6——状态参数; ρ,ρ0——流体当前密度和流体初始密度,kg/m3; E0——流体初始比内能,J/m3。 流体材料选用液态水。 管土之间采用接触描述,由于爆炸源距管道较远,爆炸地震波的传播方向可认为与管道轴向垂直。管土接触可认为是土体表面与管道外表面的法向接触,而忽略轴向的位移;因此,将管道与土体轴向摩擦系数视为无穷大,即土体表面与管道外表面之间没有切向滑动位移,同时管土界面法向接触采用罚函数的方式进行模拟,管土接触数据传递如图3所示。管内流体与管道内壁的相互作用采用流固耦合算法,耦合界面载荷传递如图4所示。 图3 管土接触数据传递示意 管道与土体作用过程中,管道接触面穿透土体目标面时产生一段穿透距离xp,而罚函数算法会在接触面与目标面节点之间加上一个弹簧,该弹簧具有罚刚度kN,此时接触力FN可以表示为: FN=kNxp (4) 图4 管道与流体之间数据传递示意 当弹簧罚刚度kN很大时,穿透距离xp很小,以至于xp接近为零,此时接触力为准确值,管道与土体之间则通过这种方式传递接触力。 管内壁与流体之间的耦合界面上需要满足运动学条件: Df=Ds (5) 式中Df——流体位移,m; Ds——管道位移,m。 流体的力通过下式传递到管道结构上: τf=Hfsτs (6) 式中τf——管道内流体压力,Pa; Hfs——管道内流体域到管道结构域的传递矩阵; τs——管道结构的应力,Pa。 管道结构接收到流体的力会产生变形,并通过下式反馈给流体: df=Hsfds (7) 式中df——当前耦合步的管道结构的位移,m; Hsf——管道结构域到管道内流体域的传递矩阵; ds——管道结构域变形后流体在网格更新后界面处的位移,m。 与自然地震波不同,爆炸地震波持续时间短、衰减快、幅值大;自然地震波持续时间长而且不会在短时间内衰减,因此不能将两种载荷等同对待[21]。但两种地震场的强度描述方法在形式上接近,都可以用加速度时程曲线进行描述。通过对第1.1节埋地炸药的爆炸计算,得到了不同时刻下爆炸冲击波在土体中的传播情况。图5示出以起爆时刻为第0 s开始计算,爆炸波在土壤中的传播过程和该时刻的加速度分布。 (a)50 μs (b)2 200 μs (c)5 000 μs (d)8 100 μs 图5 爆炸波在土壤中的传播过程及该时刻的加速度分布 由图5可以看出,炸药爆炸使土体瞬间受到挤压,在爆心处形成一个空腔,左侧土体向外形成鼓包;爆炸波向外扩散,由于左侧和下侧土体边界设定为无反射条件,图5(d)中爆炸波直接向外扩散而没有反射回来,而上侧土体为自由边界,所以出现了波反射的现象。整个过程中爆炸波加速度随时间的推移而减小,从50 μs开始时的1.9158×107m/s2,在第8 100 μs时衰减到44 608 m/s2,说明爆炸波强度在土壤中的衰减速度很快。由于模型长度所限,炸药距管道很远,爆炸波传播至管道的时间很长,所以在管道表面附近土体某点截取部分加速度时程曲线(如图6所示),并以0时刻开始计时。 图6 耦合界面处加速度-时间历程曲线 由图6可以看出,爆炸地震波在管道附近持续了6 s左右,最大加速度在第2.9 s出现,其值为96 m/s2,符合爆炸地震波幅值大的特点;持续时间比自然地震波(普遍十几秒)的持续时间短,符合爆炸地震波频率集中、持续时间短的特点。因此,该爆炸载荷可作为管道响应的载荷。 管道模型建模所根据的真实输油管道的设计压力为8 MPa,因此为了研究流动流体对管道的影响,设定管内流体的入口压力为8 MPa、流速为1 m/s。由于加速度载荷在第2.9 s时达到峰值,则取此时刻管内流体的压力和流速分布如图7所示。 (a)流体压力分布 (b)流体流速分布 从图7可以看出,流体壁面压力为8 MPa,壁面流速由于不滑移条件的存在而显示为0,内部流速为1 m/s,所以可以认为流体传递给管道壁面的压力为8 MPa。 图8示出第2.9 s时空管和充液管道的变形和应力分布。从图8(a),(b)可以看出,管道各任意截面的径向变形分布一致,说明管道在爆炸地震波作用下各个截面变形基本一致;从图8(c),(d)可以看出,管道应力分布并不均匀,这是由于管道在爆炸地震波作用下受到土体不规则的挤压力所致,而图8(d)所示应力值大于图8(c)的应力值,是由于管道受到管内流体的压力、使管道整体应力升高所致。为了进一步对比分析空管与充液管道在爆炸地震波作用时间历程中,管道迎爆面变形与应力变化情况,提取迎爆面A点的径向位移与应力随时间变化曲线如图9所示。 图8 第2.9 s时空管与充液管道的径向变形和应力分布 (a)径向位移曲线 (b)应力曲线 图9 空管与充液管道A点的径向位移和应力随时间变化曲线 从图9(a)可以看出,整个时间历程中充液管的径向位移要小于空管,这是由于内部流体压力作用于管内壁使管道向外膨胀,抵消了一部分由爆炸地震波引起的位移;同时,由于流体难以压缩,抵抗了土体对管道的挤压力。管道径向位移在第2.7 s时发生较大改变,第2.9 s时径向位移达到最大值,5 s左右径向位移值趋于平稳,这与加速度载荷随时间的变化规律相同。图9(b)所示空管应力曲线同样在第2.7 s产生一次较大应力,第2.9 s达到曲线峰值,5 s左右应力值变化趋于平稳。由于这3个时刻在曲线时间历程中具有代表性,故提取A,B两点在3个时刻的径向变形与应力汇总于表2。 表2 A,B两点的径向位移和应力汇总 从表2中的数据可以看出,在爆炸地震波传播过程的峰值第2.7 s和第2.9 s时,空管截面径向位移高于充液管,而应力远远小于充液管,说明在加速度峰值时刻管内压力抵消了部分土体对管道外壁的挤压力,造成径向位移的减小。 从管道截面位移变化看,第2.9 s和第5 s时空管的截面位移变化值变小而充液管的截面位移变化值变大。由图6可以看出,从2.9 s开始加速度载荷逐渐变小,土体对管道的挤压力变小而内压没变,所以截面位移变化值反因内压作用而变大。从应力角度看,第2.7 s时充液管截面应力变化值比空管截面应力变化值降低了93.3%,第2.9 s时降低了88.3%,第5 s时降低了57.1%;整个时间历程中,空管截面应力最大值与最小值的差为16.47 MPa,充液管为1.92 MPa,应力变化范围缩小了88%。这说明由爆炸地震波振动引起的截面应力变化由于流体的存在而变小了。 为了进一步研究管内流体运动状态对管道响应的影响,现分别就不同流体输送压力、不同流速的外爆地震波作用下的管道响应情况进行计算。 为了对比实际压力等于设计压力、小于设计压力和大于设计压力时的3种内压工况,以8 MPa为基准,选用了6,8,10 MPa三种内压。取管道中间截面和此截面上点A为研究对象,图10示出A点的径向位移和应力曲线,图11示出第2.9 s时管道中间截面各节点的径向位移和应力分布(其中180°为迎爆面)。不同输送压力下管道截面的位移和应力如表3所示。 (a)径向位移 (b)应力 图10 不同流体输送压力下A点的径向变形和应力随时间变化曲线 (a)截面径向位移 (b)截面应力 图11 不同流体输送压力下管道截面的径向位移和应力分布(第2.9 s时) 表3 不同流体输送压力作用下管道截面位移与应力汇总 图10(a)、图11(a)和表3中的径向位移值表明,在相同的爆炸地震波作用下,管道的位移响应趋势相同,基本与爆炸地震波载荷同步。由于0°,180°位置正对爆炸中心,直接受土体挤压力,此处为截面径向位移最大值发生处。图10(b)、图11(b)和表3中的应力值表明,内压越大,管道应力越大,截面应力曲线近似呈圆形分布。 随着流体压力的升高,截面最大位移增大,但最大位移与最小位移的差值变小,即截面径向位移变化范围变小了。8 MPa压力下的截面位移差值比6 MPa压力下的截面位移差值减小了1.9%;10 MPa压力下的截面位移差值比8 MPa压力下的截面位移差值减小了1.6%,说明流体输送压力越大、管道在爆炸地震波作用下越难以变形。从应力角度看,8 MPa压力下的截面应力差值比6 MPa压力下的截面应力差值减小了18.7%;10 MPa压力下的截面应力差值比8 MPa压力下的截面应力差值减小了13.1%,这说明管内流体对管道的减震作用随管内流体输送压力的增大而增大。 通过改变管道内流体输送压力可以发现,流体输送压力越大,管道越不容易发生振动,爆炸地震波对管道的振动作用越小;但随着压力的增加,管道由于自身膨胀会引起高应力,所以要保证管内流体的压力不宜过大,否则会导致管道达到屈服应力甚至强度极限而破坏。 分别设定流体流速为1,10,20 m/s,同样取管道中间截面和此截面上的点A为研究对象,图12示出A点的径向位移和应力曲线,图13示出第2.9 s时中间截面各节点的径向位移和应力(其中180°为迎爆面)。表4汇总了不同流速下截面的位移和应力。 (a)径向位移 (b)应力 图12 不同流速下A点的径向变形和应力随时间变化曲线 图12(a)、图13(a)和表4表现出的不同流速管道位移响应趋势规律与不同输送压力工况相同,基本与爆炸地震波载荷同步。图13(a)三条曲线基本重合,0°,180°位置为截面径向位移最大值发生处。图12(b)、图13(b)和表4中的应力值表明,流体压力总体上决定了截面应力值的大小,不同流速下的应力值会在此基础上波动。 (a)截面径向位移 (b)截面应力 图13 不同流速下第2.9 s时截面的径向位移和应力 表4 不同流体流速作用下管道截面位移与应力汇总 随着流体流速的升高,10 m/s流速下的截面位移差值比1 m/s流速下截面位移差值增大了0.3%;20 m/s流速下的截面位移差值比10 m/s流速下截面位移差值增大了1%,这说明流速越大,截面位移变化越大。从应力角度看,10 m/s流速下的截面应力差值比1 m/s流速下的截面应力差值增大了2.0%;20 m/s流速下的截面应力差值比10 m/s流速下的截面应力差值增大了2.6%,这说明管内流速越大,爆炸地震波对管道的作用越大,管道振动越明显。同时可以看出,A点到达最大位移的时刻与到达最大应力的时刻不一致,且A点的应力随时间变化曲线呈现出了一种震荡效果。爆炸地震波载荷在第2.9 s为峰值,但不同流速下管道截面应力峰值并不与地震加速度传播规律相同步,说明在管道内部流体流速变高后,管道响应变得更加复杂,高流速导致管道在爆炸地震波作用下出现复杂的振动效应。 表4中,随着流速的升高,截面峰值应力减小,这是因为管道内壁与流体之间存在摩阻力,流体流动一段距离会造成压降,管道越长,压降越大;由于管内的压力降低,抵抗外界载荷的能力变弱,外部压力对管道的作用效果就会越来越大,因此截面应力的响应范围随流速的升高而增大。整个时间历程中,流体流速越高,管道截面的峰值应力越小,这与第4.1节不同流体压力分析的结论相反,充分说明流固耦合作用对管道的影响不可忽略。 本文建立了埋地管道外爆流固耦合计算模型,得到了临近管道处的爆炸地震波载荷,分析空管和充液管在爆炸地震波作用下的响应情况,得出以下结论。 (1)利用有限元方法模拟埋地炸药爆炸并得到了管道附近的爆炸载荷,并将此爆炸波用加速度时程描述,视为爆炸地震波。通过建立管土接触方式、管内流体与管道内壁的流固耦合方法,实现了土体-管道-管内流体的流固耦合数据传递。 (2)通过对比空管和充液管在相同爆炸地震波作用下的响应情况,发现管内流体可降低管道在爆炸地震波作用下的应力响应范围,整个时间历程中充液管应力范围比空管的应力变化范围缩小了88%。说明由爆炸地震波振动引起的管道截面应力变化由于流体的存在而变小。 (3)随着流体输送压力的升高,管道截面峰值应力逐渐增加,但应力变化范围逐渐降低,截面应力差值从18.7 MPa降到13.2 MPa,这说明管内流体输送压力越大,爆炸地震波作用于管道的振动效果越小。 (4)随着流速的升高,管道截面峰值应力逐渐下降,但应力变化范围逐渐增大,截面应力差值从15.2 MPa升到15.9 MPa,这说明管内流速越大,爆炸地震波对管道的作用越大,管道振动越明显。

1.2 耦合界面数据传递方法
2 爆炸地震波的计算





3 爆炸地震波作用下运动流体对管道响应的影响分析


4 不同流体参数对管道响应的影响分析
4.1 不同流体输送压力对管道响应的影响




4.2 不同流体流速对管道响应的影响



5 结论
