多尺度空间下的隧道裂缝与渗水区域检测
2020-01-01贾东峰张伟平刘燕萍
贾东峰, 张伟平, 刘燕萍
(1.同济大学 土木工程学院, 上海 200092; 2.同济大学浙江学院, 浙江 嘉兴 314051)
在隧道结构的安全检测中,裂缝检测是十分重要的检测项目.隧道裂缝检测的传统方法以人工判读与记录为主,少量以动态检测车辅助,通过各工区相互配合,在线路无运营任务时对隧道管壁进行人工筛查.这种方法工作效率低,人工成本高且容易受人工主观判断力的影响造成漏测、误测.随着地下结构检测技术的发展,一些自动化的裂缝检测技术得到了有效地发展.这些隧道裂缝自动化检测技术可以分为三类:第一类是基于隧道自身形变的固定式检测方法.通过测量隧道形变或者布设形变传感器获取隧道局部的形变及裂缝信息,并对形变和裂缝进行分析和评价,获取局部区域的安全状况;第二类是通过光学成像技术,获取隧道内部的影像数据,并通过数字图像处理的相关技术,获取隧道内部的裂缝信息;第三类是通过雷达探伤技术获取隧道内部管壁的裂缝形状及其深度信息.近年来,一些成熟的隧道裂缝检测系统,如德国的GPR5000隧道检测车[1]、日本基于电荷耦合器件(charge couple device,CCD)线阵列的隧道裂缝检测系统[2]等,在隧道内部的裂缝检测中可以发挥重要的作用,但是其设备成本高,不易于维护,同时由于这些国家的技术屏蔽,阻碍了这些系统的推广和发展.
三维激光扫描技术不仅可以获取隧道内部的点云数据,而且可以获取其高分辨率的全景影像信息,这些影像数据包含了隧道内部的裂缝、渗水信息,可以有效地应用到隧道的裂缝检测中.对于基于图像的隧道裂缝检测方法,由于其成本低,易于开展和处理,近年得到了广泛的研究,学者们提出了许多成熟的算法.Siriphan[3]提出了基于中值滤波的裂缝检测算法,首先采用中值滤波对影像进行平滑处理,滤除环境噪声的影响,起到图像增强的效果,成为目前广泛使用的一种裂缝影像预处理方法.Muduli等[4]根据数字图像处理理论提出了一种快速裂缝提取算法,通过对Canny算子进行改进,提高了裂缝图像的峰值信噪比和裂缝的提取精度.Sunil等[5]根据裂缝的特点,提出多尺度的裂缝提取算法,根据不同尺度的裂缝形态特点,采用不同的边缘提取算法对其进行识别,实现不同尺度裂缝的检测与提取.Hatada等[6]针对一般算法无法保持裂缝边缘连续性的特点,提出了一种具有方向跟踪的定向滤波算法,该算法根据裂缝的形态特征进行边缘提取,可以有效保证裂缝边缘的完整性.Kovesi[7]采用相位一致法有效去除了图像中的高频噪声,提高了裂缝提取的精度.王平让等[8]提出了一种基于十字模板的裂缝提取算法,通过种子点进行生长,可以有效避免裂缝的重复标记,该算法可以有效应用于隧道图像渗水区域的提取.沈瑜[9]提出了一种优化的隧道裂缝检测算法,可以有效提高高频子带的稳定性,同时采用Canny算法对低频子带进行边缘提取,提高了裂缝边缘的完整性.文献[10-13]分别基于数学变换、灰度阈值分割、神经网络和纹理特征等方法,实现了裂缝的提取.但是由于裂缝自身特性的差异,上述方法对裂缝图像进行提取过程中未从裂缝的物理特性进行分析,容易受到伪裂缝信息的干扰,很难取得稳定的效果.
针对隧道内部裂缝的特点,本文基于点云影像提出了不同尺度空间下的裂缝渗水区域识别与检测算法.针对不同尺度的隧道裂缝,通过定义尺度空间,提出了一种融合型图像检测算子,实现不同尺度和形态裂缝渗水区域检测.
1 隧道裂缝的物理特点
隧道内部的特殊环境使得目前对其裂缝的检测依赖于人工交互式普查.隧道内部的裂缝不同于道路、桥梁结构中的裂缝,其宽度狭窄,噪声多,容易受到管线、管壁接缝等伪裂缝形态的影响.同时由于隧道内部缺少光照,在人工光照下获得的图像容易发生曝光过度或量化不足,因此传统的图像处理算法并不适用隧道裂缝的提取,需要根据隧道裂缝的物理特点,提出新的裂缝检测算法.
隧道裂缝具有以下物理特点:① 宽度狭小,多数隧道裂缝宽度低于0.75 mm;② 在图像中占有的像素比例较小,且没有明显的双峰特性;③ 隧道裂缝具有不同的形状和尺度特征;④ 边缘比较粗糙,且空间走势呈自由曲线.
2 本文裂缝提取算法
隧道裂缝在物理形态上具有多样性,容易受到伪裂缝信息的干扰.在空间特点上也具有尺度多样性,需根据其尺度特征,设计合适的检测算子,实现不同尺度和形态的裂缝检测.
(1) 尺度空间构建
尺度空间构建是为了模拟图像数据的多尺度特征.对于预处理过的隧道内部图像,其裂缝在图像上具有多尺度特征.通过建立尺度空间,可以实现不同尺度下裂缝特征的提取.根据高斯核函数构建的尺度空间如式(1)所示.
L(x,y,σ)=G(x,y,σ)*I(x,y)
(1)
式中:σ为高斯核函数的尺度因子;L(x,y,σ)为尺度空间函数;G(x,y,σ)为高斯核函数;I(x,y)为输入图像,尺度空间是不同尺度高斯核函数和图像的卷积.
(2)
通过改变σ的大小可以控制图像被平滑的程度,值越大图像被平滑得越厉害.通过选择不同大小的尺度因子σ来突出图像在不同尺度上的特征,这样就保证了同一特征在不同尺度上时都可以被提取出来,从而使检测出的特征具有尺度不变性.
(2) 裂缝检测算子定义
可以根据图像的概率统计特性,对图像中裂缝进行提取.文献[14]和文献[15]分别针对图像的统计特性,深入论述了基于图像统计特性的特征像素提取算法,并提出了相应的检测算子.通过对文献[14]算子进行改进,定义比率检测算子D1表示相邻区间像素均值的比率(rij,rji),对于图像中的任意两个相邻区间i和j,对检测算子D1的响应可表示为
rij∶rji=1-min(μi/μj,μj/μi)
(3)
式中:μ为采样均值,对于三个相邻区间k,i和j,则检测算子D1的响应可表示为
D1=min(rik,rij)
(4)
可以发现,检测算子D1是关于像素(x,y)的邻域大小m×n和夹角θ的分布函数,其中θ的定义如图1所示.
检测算子D1对图像统计特性中的均值比较成分具有较好的表现,但是对于算子窗口中心不在裂缝边缘的情况下,其检测效果较差.因此定义检测算子D2,其意义为用概率分布函数模型表示裂缝强度函数,数学模型为
(5)
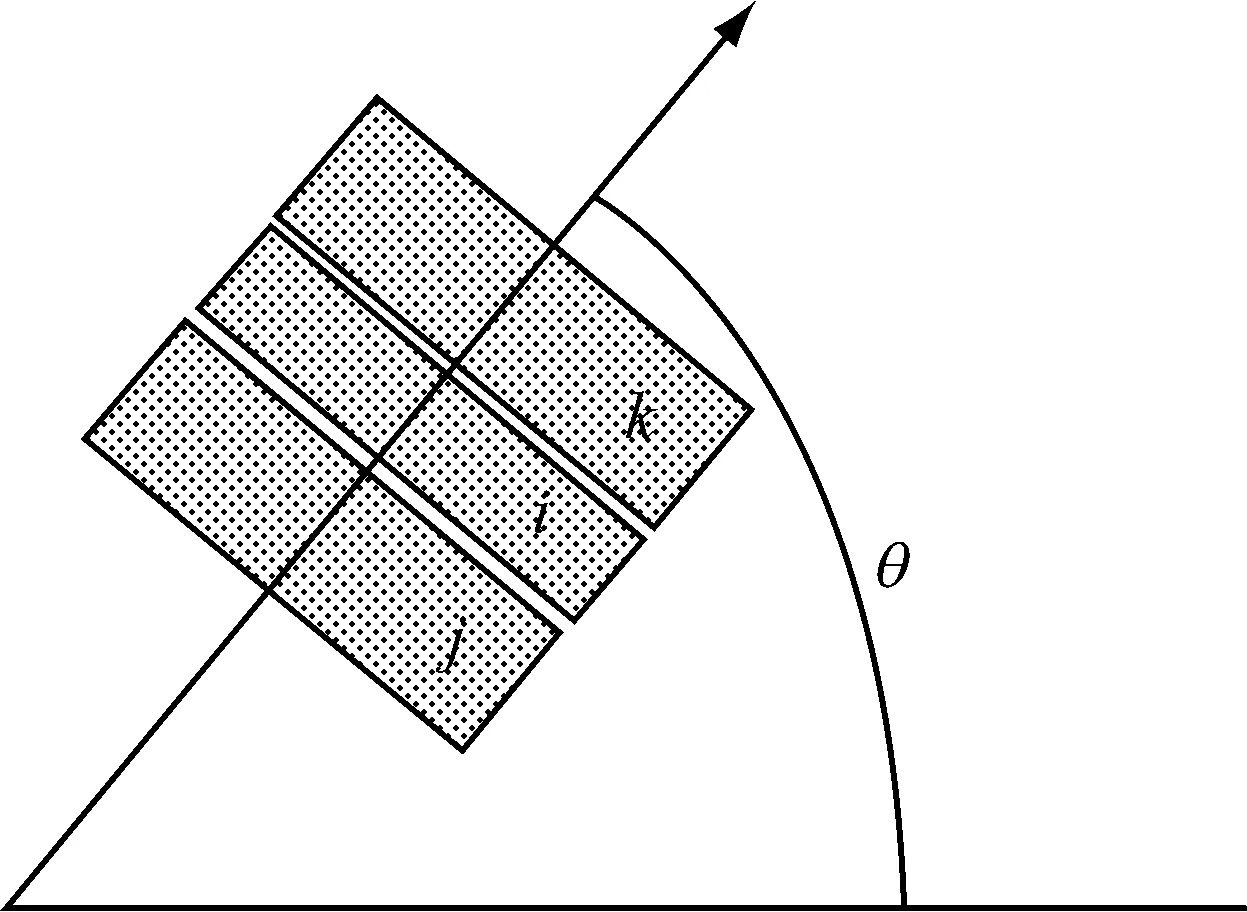
图1 θ角的定义
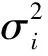
(6)
该算子既可以保持对带状裂缝检测的稳定性,同时对于灰度值较高的小裂缝,可以恢复其对高灰度值的敏感特性,得到较多的响应边缘像素值,即可获取边缘特征点的尺度和位置.为了更精确地定位所有边缘特征点,对提取的极值点做二次函数拟合,再按泰勒级数展开,如式(7)所示.
(7)
式中:X=(x,y,σ)T.D(X)对X求导数,当导数值为零时,则:
(8)
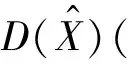
(9)
通过式(7)~(9)运算和操作,可以实现不同尺度裂缝的提取.由于隧道图像中含有凹槽和管线,在边缘点计算中会被当作裂缝边缘进行提取,因此需要设计阈值进行过滤,本文通过计算裂缝的宽度对其进行过滤.凹槽在图像上呈正方形,其宽度一般为8 cm,管线的宽度一般为1 cm,而在隧道中裂缝大于0.75 mm时已经达到报警级别,鲜有裂缝宽度大于1 cm,且不同于管线,裂缝的宽度不均匀,对于裂缝宽度大于1 cm的情况,可通过最大宽度和最小宽度的差值进行伪裂缝的排除.
3 实例分析
3.1 裂缝提取精度分析
选取三维激光扫描仪获取的隧道内部全景点云图像,根据高斯投影模型进行转换,然后按照300×300像素图幅对图像进行分割,并通过本文提出的裂缝提取算法进行处理.图2所示为图像裂缝提取过程,其中图2a~图2d是图像预处理过程,分别采用对比度拉伸增强裂缝图像的对比度,并根据滤波算法过滤背景中的噪声,然后生成二值图像.图2e为采用本文提取算法得到的裂缝边缘,从图中可以看出算法对于裂缝边缘的识别度较高,但是一些伪裂缝边缘也得到了提取,通过设置宽度阈值为1 cm,即裂缝宽度大于1 cm为伪裂缝,小于1 cm为真实裂缝,图2f为阈值过滤后的结果,图中裂缝边缘用虚线显示.通过过滤实现了裂缝的准确识别和定位.
为了进一步分析判断本文算法的准确率,通过三组不同尺寸的裂缝图像进行分析,三组图像中的裂缝已经提前进行人工标定,其长度已知,图3为对第一组图像进行裂缝提取的结果.对于人工标定宽度大于0.75 mm的裂缝定义为大裂缝,宽度大于0.5 mm而小于0.75 mm的裂缝定义为中等裂缝,宽度小于0.5mm的裂缝定义为小裂缝.图中的裂缝分别符合对不同尺度裂缝的定义.如图3b、3d和3f所示,通过本文算法、提取和阈值过滤,能够准确找到图中裂缝的位置.并且对大裂缝的边缘提取较为完整(图3b),对中等裂缝的提取过程产生了较为明显的断裂(图3d),对小裂缝的边缘提取则精度较差(图3f).
对三组图像分别进行提取同时和人工标定值进行比较,表1所示为本文算法和人工标定值的对比分析.从表1中可知,本算法对于大裂缝的提取很准确,其长度和人工标定值比较相差(0.8 cm,0.96 cm,0.99 cm),正确率达到了90%;对于中等裂缝,由于存在断裂,所以其提取精度有所退化,与人工标定值比较,其长度相差(3.6 cm,4.1 cm,3.81 cm),

a 原始图像

b 对比度增强

c 滤波处理

d 图像二值化

e 边缘提取
f 阈值过滤

a 大裂缝图像

b 提取结果

c 中等裂缝图像
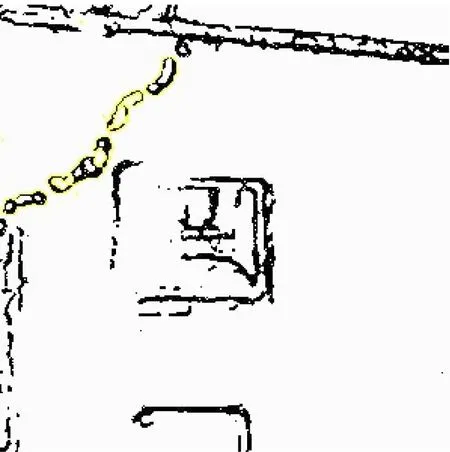
d 提取结果

e 小裂缝图像

f 提取结果

表1 本文算法与人工标定裂缝长度对比
正确率达到了70%;对于小裂缝的提取精度较差,从图3e、3f可以看出,部分裂缝由于存在误判,并未得到有效提取.同时对于已经提取部分的断裂较大,与人工标定值比较,其长度相差(10.2 cm,11.95 cm,5.95 cm),正确率为25%.因此,有待提高对断裂部位的连接,同时降低可能引入的随机噪声.
同时,为了进一步分析本文算法的精度,分别采用Muduli算法和Kovesi算法对三组图像进行处理和提取,对其结果进行对比分析.表2所示为不同算法的提取结果.从表2中可知,对于图中大裂缝,三种方法均可到达较高的提取精度,与标定值对比,Kovesi算法对大裂缝的提取更加精确,其提取正确率达到了95%;对于图中中等裂缝的提取,本文算法的精度优于Muduli算法和Kovesi算法,提取正确率为80%;对于小裂缝的提取,从表中可以看出,Kovesi算法对小裂缝的提取效果较差,几乎不能识别和提取微小裂缝.同时由于噪声干扰,Muduli算法对小裂缝的提取精度也较差,其正确率为14%.

表2 不同算法的裂缝长度分析对比
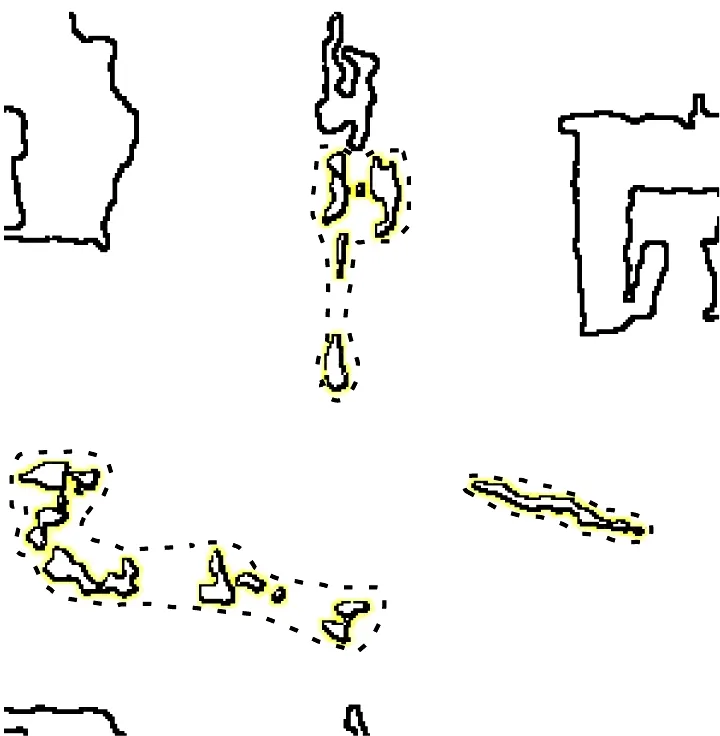
3.2 渗水区域检测
与裂缝图像相比,渗水区域的面积较大.对于一幅含有渗水区域的图像,与图像背景灰度值相比,渗水区域的灰度值较低,背景部分的灰度值较高.可通过对比度拉伸,提高图像中明、暗部分的灰度差异,进一步提高渗水区域的识别度.图4a是含有渗水区域的隧道图像.图4b是图像对应的直方图.
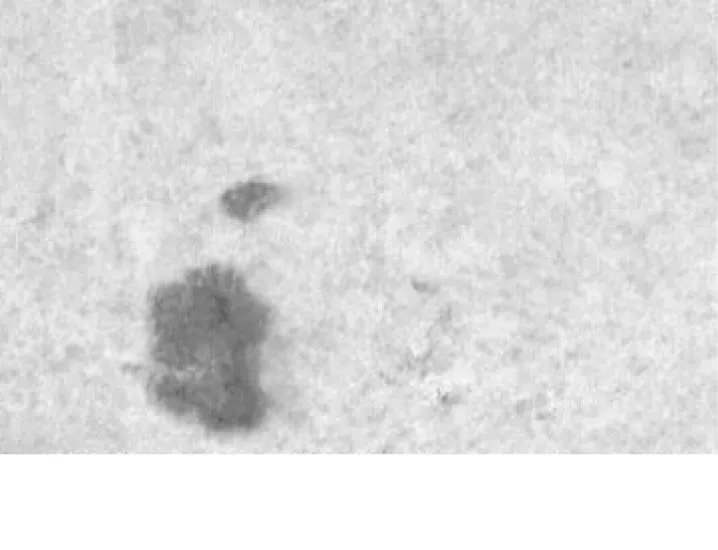
a 渗水区域图像
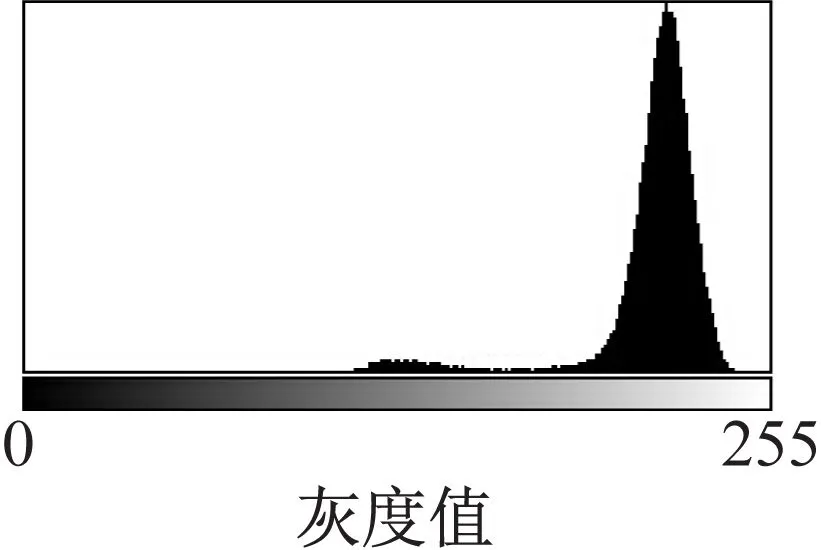
b 图像直方图
采用分段线性拉伸的方法,进一步降低暗色部分的灰度值,提高明亮部分的灰度值,通过对比度拉伸后的图像如图5所示.
采用本文提出的边缘检测算法对其进行边缘提取,设置偏移量阈值为0.08,所得结果如图6c所示.6a是采用Canny算子获取的渗水区域边缘,从图中可以看出,Canny算子提取的边缘较为完整,边缘线性的连接程度也较高,但是Canny算子受噪声的影响较大,由于图像中含有一些噪声,采用Canny算子很难进行噪声的过滤.图6b为采用Sobel算子获取的渗水区域边缘,从图中可以看出Sobel算子也可以获取渗水区域的有效边缘,对噪声也有一定的抑制能力,但是不能完全排除检测结果中出现的虚假边缘,虽然Sobel算子的定位精度较高,但是检测的边缘容易出现多像素宽度.从图6c中可以看出,本文算法可以获得较好的渗水区域边缘,并且和Canny算子、Sobel算子相比,在对比度较高的情况下,本文算法的抗噪性较好,可以较好地过滤背景部分的椒盐噪声,同时获得完整连贯的边缘.
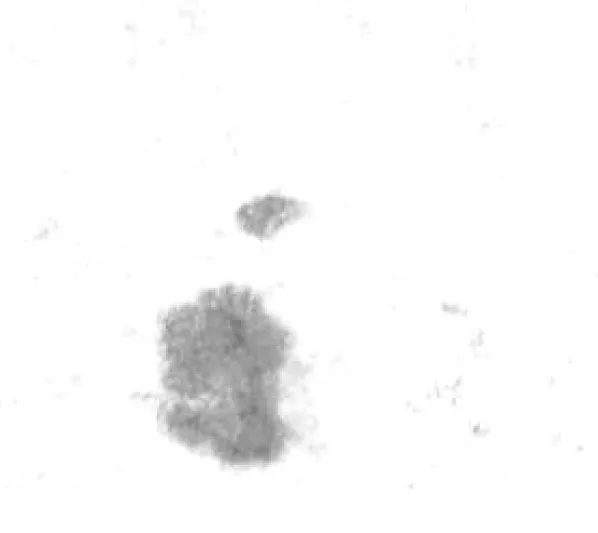
a 灰度拉伸后图像

b 图像直方图

a Canny算子

b Sobel算子

c 本文算法
4 结语
点云影像包含了隧道内部裂缝和渗水区域的信息,可以有效地应用到隧道裂缝和渗水检测中.根据隧道内部裂缝的物理特点,提出了一种不同尺度空间下的隧道裂缝提取算法.该算法不仅可以保持对带状裂缝检测的稳定性,同时对于灰度值较高的小裂缝,可以恢复其对高灰度值的敏感特性,得到较多的响应边缘像素.通过对实际的隧道图像进行测试分析,本文算法可以有效排除伪裂缝信息的干扰,对不同尺度的裂缝进行准确识别和定位.同时对于宽度大于0.5 mm的裂缝提取精度较高,对于宽度小于0.5 mm的裂缝提取精度略差.采用本文算法对渗水区域的识别提取精度较高,同Canny算子和Sobel算子相比,本文算法的抗噪性较好,可以较好地过滤背景部分的椒盐噪声,同时获得完整连贯的边缘.
