城市乔木树种多样性遥感反演方法研究
2019-12-31靖传宝周伟奇钱雨果
靖传宝,周伟奇,*,钱雨果
1 中国科学院生态环境研究中心城市与区域生态国家重点实验室,北京 100085 2 中国科学院大学,北京 100049
城市乔木树种多样性会影响其提供生态系统服务的能力,对改善城市环境、维持城市可持续发展有着重要的意义。研究表明,城市乔木树种多样性会在不同程度上影响城市树木在降雨截留[1]、气温调节[2]、污染物削减[3]、鸟类[4]和昆虫多样性维护[5]、情绪调节[6]等方面的生态系统服务。量化城市乔木树种多样性是定量研究其生态系统功能和服务的前提。随着全球城市化的快速推进,外来树种被大量引入城市,导致城市内树种多样性水平变化剧烈[7],迫切需要快速、准确量化城市乔木树种多样性水平的方法。传统的量化方法主要基于地面调查,效率低、成本高,难以满足及时掌握城市乔木树种多样性信息的需求。因此,发展基于遥感技术,能够准确高效地量化城市乔木树种多样性的方法具有重要的意义。
光谱变异性假说(Spectral Variation Hypothesis,SVH)和生产力假说(Productivity Hypothesis)是基于遥感技术反演乔木树种多样性的理论基础。其中,前者认为光谱异质性(光谱异质性水平可采用分析单元内部的光谱标准差表示[8])越高,乔木树种的多样性也越高[9];后者认为乔木树种丰富度与生产力存在相关关系[10]。可采用衡量生产力的归一化植被指数(Normalized Difference Vegetation Index,NDVI),常用于反映乔木树种的多样性水平[11-12]。
上述假设在自然生态系统中得到了验证,并应用于乔木树种多样性的遥感反演。许多学者研究发现遥感影像各波段及NDVI的标准差与乔木树种多样性之间的关系满足光谱变异性假说和生产力假说,并进一步应用多元回归、神经网络等方法构建了光谱变异性与乔木树种多样性之间的关系模型,用于快速、准确地反演了乔木树种的多样性水平。但是,鲜有学者探讨上述两种假说在城市中的适用性及其应用。其可能原因是:自然生态系统中的遥感反演方法无法直接应用于城市生态系统中。自然生态系统具有景观相对均质、乔木树种多样性水平低等特点,采用中、低空间分辨率影像能够较准确地刻画其乔木树种多样性水平[13-14]。而城市生态系统中的景观异质性高、乔木斑块面积小、单位面积的树种多样性水平高,中、低空间分辨率遥感影像通常为乔木斑块和非乔木斑块的混合像元,难以精确刻画城市内的乔木树种多样性水平。因此,有必要在城市区域探讨光谱变异性假说和生产力假说的适用性,并基于上述两种理论探索城市乔木树种多样性遥感反演方法。
本文将通过探究高空间分辨率遥感数据的各波段光谱异质性、NDVI指数的异质性与乔木树种多样性水平之间的相关关系,发展基于高空间分辨率遥感数据的城市乔木树种多样性的快速反演方法。试图回答以下科学问题:光谱变异性假说和生产力假说是否适用于城市乔木树种多样性的反演研究?
1 数据与方法
1.1 研究区
北京是中国首都及中国四个特大城市之一,是快速发展的典型城市[15]。1978—2016年,城市常住人口快速增长,从1987年的871.5万增加到2016年的2172.9万,年均增加34.2万,年均增长2.4%[16]。北京属于半湿润大陆性季风气候,夏季高温多雨,冬季寒冷干燥,本地乔木树种以暖温带阔叶林为主,同时有大量外来引进乔木树种。
研究区选取北京五环内区域(39°28′—41°25′N,115°25′—117°30′E),占地面积667.81 km2。该区域是北京的主要建成区,截止2009年,其植被覆盖度为32.8%[17]。区域内乔木丰富度为92种,常见种为龙爪槐(Sophorajaponica)、圆柏(Sabinachinensis)、银杏(Ginkgobiloba)和毛白杨(Populustomentosa),4种树种数量占区域乔木总数量的35%。其中,龙爪槐(S.japonica)数量最多,占区域总乔木数的12.6%。同时,乔木丰富度表现出空间异质性,居民区、社区公园、文教区内的丰富度明显高于其他景观类型[18]。由于快速地城市化,研究区内的外来物种比例持续增长,当前已增加至50%左右[19]。因此,北京五环内区域可作为在快速城市化背景下探究城市乔木树种多样性遥感反演方法的理想研究区。
1.2 数据
1.2.1乔木树种多样性数据
居民区分布广泛、易于调查,有利于发展乔木树种多样性反演方法,因而本研究针对居民区开展乔木斑块多样性地面调查。研究首先基于高分影像以均匀取样为原则初步勾画乔木样地斑块,并于2014年6月 至8月期间开展地面调查和边界优化工作,共收集了395个有效的乔木斑块(图1),斑块面积分布如图2。乔木斑块内物种数最大为20,最小为1,平均值为3.8(图3)。
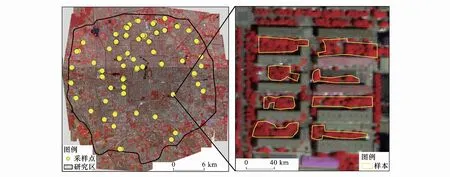
图1 研究区及采样点研究区内样地分布乔木斑块Fig.1 The study area and the sampling points Distribution of samples Tree patches

图2 样地的面积Fig.2 Area of sample plot

图3 样地的物种数Fig.3 The tree species of sample plot
参考已有研究[20],选择香浓维纳指数和辛普森指数表征斑块的乔木树种多样性,两个指数越大则多样性水平越高,但各有偏重。香浓维纳指数同时考虑物种数和物种比例,而辛普森指数侧重对普通物种的度量,两者常配合使用。具体公式如下:
(1)
(2)
式中,H′为香浓维纳指数,D为辛普森指数,S为物种数目,Ni为种i的个体数,N为群落中全部物种的 个体数。
1.2.2光谱异质性数据
1)样地的光谱异质性。光谱异质性以乔木斑块的各波段或指数的光谱标准差来表征。本研究选用高空间分辨率的GeoEye-1遥感影像,在乔木斑块尺度上提取光谱异质性特征。该影像包括四景数据,获取时间均为2009年6月,具有全色波段(Pan:0.45—0.90 nm)、蓝波段(Blue:0.45—0.51 nm)、绿波段(Green:0.51—0.58 nm)、红波段(Red:0.655—0.690 nm)和近红外波段(NIR:0.78—0.92 nm)五个波段,全色波段空间分辨率为0.5 m,其他波段空间分辨率为1.65 m,整个研究区内无云。对该影像处理工作主要包括几何校正,波段合成和影像镶嵌。几何校正以Google影像为基准。研究共量化了6种光谱异质性,包括NDVI标准差(NDVISD)、蓝波段标准差(BlueSD)、绿波段标准差(GreenSD)、红波段标准差(RedSD)、近红外波段标准差(NIRSD)和全色波段标准差(PanSD)。
乔木斑块多样性地面调查2014年6月至8月,而因高空间分辨率遥感数据获取的限制,遥感影像获取时间为2009年6月,但本研究通过选择居民区内样地的方式,能够使两种数据在时间上达到匹配。居民区建成后,其内部绿地极少重新规划,乔木树种多样性水平将基本不变,即使研究区是快速发展的典型城市,其居民区仍可认为是树种多样性的稳定的区域。同时,选择居民区时,本研究仅选择2009年6月至2014年8月期间一直存在的居民区。
2)研究区范围的光谱异质性。本研究选择已有的研究区土地利用分类结果(图4),并以分类结果中林地斑块作为乔木斑块,在乔木斑块尺度上量化整个五环范围内乔木斑块的光谱标准差。该分类结果以上述GeoEye遥感影像为数据源,采用面向对象的图像处理技术和非监督分类方法并结合手动修改获得。其中,分类器选择支持向量机,具体参数设置[21]:Kernel为rbf神经网络,C=100000,gamma=0.0001。土地利用类型包括林地、草地、耕地、湿地、建设用地、裸地和其他用地。总体精度和Kappa系数分别为95.50%和0.89,其中林地的用户精度和制图精度分别为96.02%和93.56%。

图4 土地利用分类图Fig.4 Land use classification map
1.3 方法
参照自然生态系统的乔木树种多样性反演方法,构建本研究的思路(图5)如下:1)基于偏相关分析方法,探究乔木树种多样性与光谱异质性之间的相关关系,检验光谱变异性假说和生产力假说是否适用于城市区域;2)构建反演模型,探究高空间分辨率遥感影像对城市乔木树种多样性水平的反演能力。

图5 本研究技术路线Fig.5 Flowchart of the analysis
1.3.1相关性分析
偏相关分析中,将面积作为控制变量,并分两部分展开:1)分析光谱异质性数据(NDVISD、GreenSD、RedSD、PanSD、BlueSD和NIRSD)之间的相关性,用于探讨自变量之间是否具有多重共线性,为多元线性回归模型和BP神经网络模型反演模型的选择和构建提供重要依据;2)分析光谱异质性与乔木树种多样性指数(香浓维纳指数和辛普森指数)之间的相关性,据此选择与乔木树种多样性数据显著相关的光谱异质性变量构建多元线性回归模型和BP神经网络模型。
1.3.2反演模型构建
自然生态系统中,常基于多元线性逐步回归模型和神经网络模型反演乔木树种多样性水平。本研究试图从线性和非线性两个维度刻画乔木树种多样性与光谱异质性之间的关系,因而同时选择了多元线性逐步回归模型和神经网络模型反演。为使得分析结果具有可比性,两模型均选用了相同的自变量、因变量、训练样本集和模型精度验证样本集。参考已有研究[22],随机选择的365个乔木斑块样本构成训练样本集,剩余的30个样本组成模型精度验证样本集。
多元线性逐步回归模型用于构建乔木树种多样性与光谱异质性之间的线性关系,其构建包括以下几个步骤:1)基于光谱异质性数据与乔木树种多样性数据之间的相关性分析结果,分别筛选出与香浓维纳指数和辛普森指数显著相关的影像因子作为自变量;2)对上述自变量分别与两种多样性指数进行多元线性逐步回归分析,得到香浓维纳指数和辛普森指数的多元线性回归模型;3)应用该模型对测试样本集进行反演。
BP神经网络模型[23]具有强大的非线性映射能力,理论上可以逼近任意函数,用于构建乔木树种多样性与光谱异质性之间的非线性关系。该模型由输入层、隐含层和输出3层结构构成。其中,输入层由输入变量组成,即光谱异质性数据;输出层由输出数据组成,即乔木树种多样性水平。参照已有研究,模型参数设置如下:选择与香浓维纳指数和辛普森指数显著相关的光谱异质性数据作为模型输入,分别以斑块香浓维纳指数和辛普森指数作为模型输出,网络的拓扑结构均为(5,7,1)和(6,7,1),隐含层传递函数采用S型函数(transig),输出层传递函数采用线性函数(purelin),网络训练的最大训练次数为1000次,训练函数为tranlm。
1.4 模型精度评价
模型精度评价以乔木树种多样性反演结果与实际多样性水平之间的差异为依据。采用决定系数(R2),均方根值误差(root mean square error,RMSE)和平均偏差(mean normalized bias,MNB)[24]三个指标评估多元线性模型和BP神经网络模型模型的反演精度。其中,R2能够反映回归方程对因变量y总变异的解释比例,R2越大则反演模型精度越高。RMSE可以评估反演值与真实值之间的误差,RMSE越小则反演模型精度越高。其公式为:
(3)
MNB用以评估系统误差,MNB越小则反演模型精度越高。其表达式为:
MNB=100mean(xi-x)
(4)
2 结果
2.1 偏相关分析结果
1)各光谱异质性特征之间普遍存在正相关关系(表1)。其中,BlueSD、GreenSD以及RedSD两两之间的线性相关性最强(R=0.925-0.960,P<0.01);PanSD与BlueSD、GreenSD以及RedSD之间的线性相关强度次之(R=0.748-0.815,P<0.01);NIRSD与PanSD相关性相对较低(R=0.413,P<0.01),与GreenSD、RedSD、BlueSD以及NDVISD之间相关性不显著。
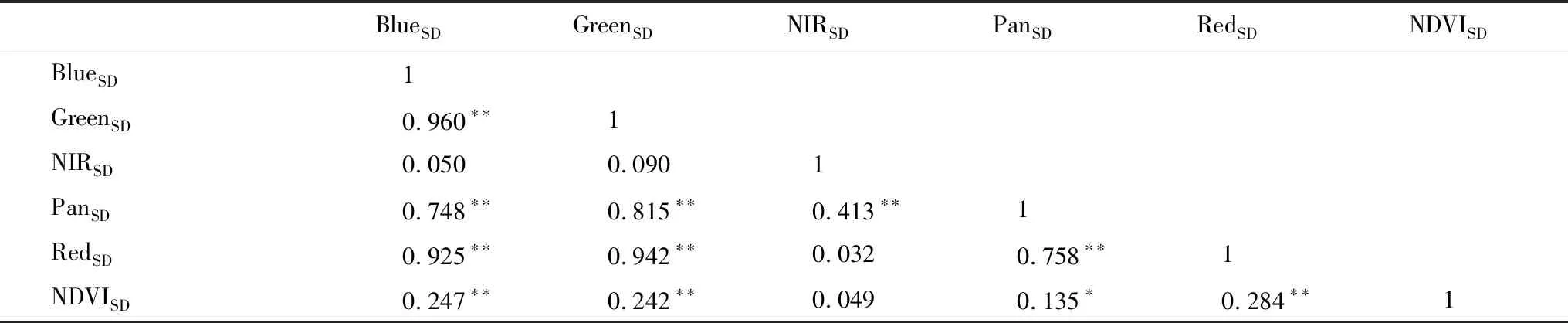
表1 光谱异质性数据相关性Table 1 Correlation analysis of spectral heterogeneity′s data
显著性水平:**P<0.01,*P<0.05;控制变量:样地面积;NDVI标准差(NDVISD)、蓝波段标准差(BlueSD)、绿波段标准差(GreenSD)、红波段标准差(RedSD)、近红外波段标准差(NIRSD)和全色波段标准差(PanSD)
2)乔木树种多样性与光谱异质性特征之间存在普遍正相关性。由表2可知:香浓维纳指数和辛普森指数均与NIRSD线性相关性不显著(P>0.05),与GreenSD、RedSD、BlueSD、PanSD和NDVISD呈现显著正相关(P<0.05)。但相关程度存在差异,与香浓维纳指数的相关强度由高到低分别为GreenSD、RedSD、BlueSD、PanSD和NDVISD,其皮尔森系数分别为0.229、0.214、0.204、0.197和0.168;与辛普森指数的相关强度由高到低分别为PanSD、NDVISD、GreenSD、RedSD和BlueSD,其皮尔森系数分别为0.202、0.189、0.174、0.144和0.136。

表2 光谱异质性数据与乔木树种多样性数据相关性Table 2 Correlation analysis between species diversity and spectral heterogeneity′s data
显著性水平:**P<0.01,*P<0.05;控制变量:样地面积;NDVI标准差(NDVISD)、蓝波段标准差(BlueSD)、绿波段标准差(GreenSD)、红波段标准差(RedSD)、近红外波段标准差(NIRSD)和全色波段标准差(PanSD)
2.2 模型选择及应用
1)多元线性逐步回归模型。利用训练样本集分别拟合获得香浓维纳指数和辛普森指数的多元线性逐步回归模型。在多元线性逐次回归分析中,剔除了PanSD和RedSD,得到香浓维纳指数的线性回归模型:
Y1=0.029X2+0.002X6-0.026X1+0.410(R2=0.094,P=0.00)
(5)
其中,Y1为香浓维纳指数、X1为BlueSD、X2为GreenSD、X6为NDVISD;
剔除了GreenSD、RedSD和BlueSD,得到辛普森指数的线性回归模型:
Y2=-0.005X5+0.001X6+0.280(R2=0.080,P=0.00)
(6)
其中,Y2为辛普森指数,X5为PanSD、X6为NDVISD。
2)模型精度分析。应用以上多元线性回归模型,以及相同训练样本得到的非线性的BP神经网模型,分别估计香浓维纳指数和辛普森指数。结果显示,BP神经网模型香浓维纳指数和辛普森指数的预测能力均显著高于多元线性回归模型。在多元逐步回归预测模型中(图6),香浓维纳指数模型的决定系数(R2)、均方根值误差(RMSE)和平均偏差(MNB)分别为0.167、36.27%和52.28%;辛普森指数模型的决定系数(R2)、均方根值误差(RMSE)和平均偏差(MNB)分别为0.25、10.69%和19.95%。在BP神经网络模型中(图7),香浓维纳指数模型的决定系数(R2)、均方根值误差(RMSE)和平均偏差(MNB)分别为0.57、24.04%和42.16%;辛普森指数模型的决定系数(R2)、均方根值误差(RMSE)和平均偏差(MNB)分别为0.72、4.44%和15.95%。

图6 香浓维纳指数反演值与实际值之间的关系Fig.6 The relationship between Shannon-Wiener′s calculated values and actual values

图7 辛普森指数反演值与实际值之间的关系Fig.7 The relationship between Simpson′s calculated values and the actual values
3)基于上述模拟结果,选择BP神经网络对北京市的乔木树种多样性水平进行反演。以研究区的土地利用分类结果中提取的乔木斑块为分析单元,应用BP神经网络模型开展了研究区乔木树种多样性预测,并基于归一化后的预测值(相对预测值)绘制研究区乔木树种多样性空间地图(图8、图9)。
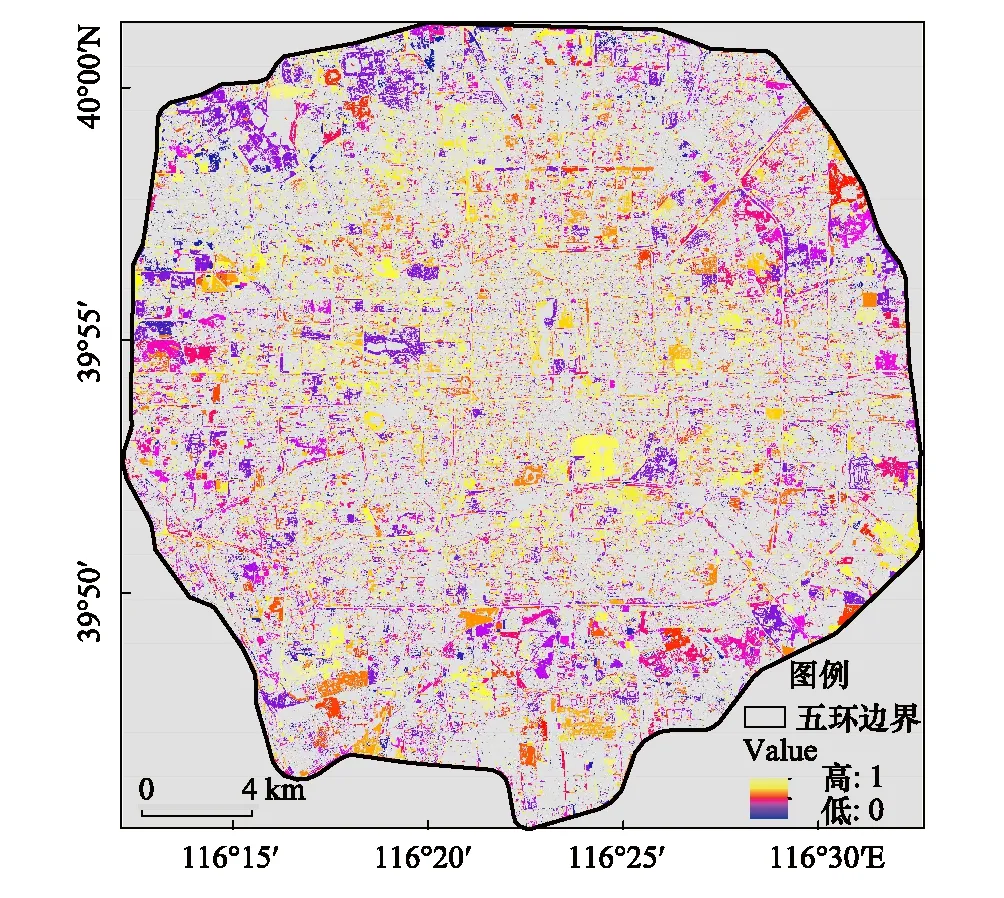
图8 香浓维纳指数空间分布图Fig.8 The spatial distribution of Shannon-Wiener index

图9 辛普森指数空间分布图Fig.9 The spatial distribution of Simpson index
4 讨论与结论
在城市中,光谱变异性假说和生产力假说得到了更好地诠释。研究发现,与自然生态系统相比,城市生态系统中的乔木树种多样性与遥感影像光谱异质性之间不仅存在类似的正相关关系[25],甚至该关系显著性和相关性水平更高[8]。可能的原因是:1)样本中像元数量的差异。在自然生态系统中,一个样本仅有少量像元,如9个像元;而本研究以斑块为分析单元,单个样本点包含的像元数是前述样本的几十倍甚至几百倍;2)遥感影像分辨率的差异。一株乔木冠幅等于一个像元的大小是探究乔木树种多样性水平与遥感影像光谱异质性关系的最理想情况。而实际研究中,由于不同乔木具有不同的冠幅,难以找到完全与冠幅相匹配的遥感数据。针对同一样本,与最理想情况的光谱异质性水平相比,中等分辨率遥感影像的光谱异质性水平常偏低,高空间分辨率遥感影像的光谱异质性水平常偏高;3)乔木树种多样性数据分布特征的差异。与自然生态系统相比,城市生态系统中乔木树种多样性的最低水平相似,而由于城市中大量地进外来物种[7],其内部乔木树种多样性水平具有更最高的水平,进而导致其极差更大。城市中乔木斑块小、异质性强,如应用中等空间分辨率的遥感影像,样地内包含的像元数较少、像元过大,难以刻画其乔木树种多样性水平,因此,本研究建议采用高空间分辨率遥感影像探究城市乔木树种多样性水平。
神经网络模型在刻画非线性关系时具有明显的优势[26],更适合城市乔木树种多样性的反演。结果显示,基于BP神经网络构建非线性回归反演能力明显优于多元线性回归模型(图6、7)。这说明非线性模型能够更好地刻画城市乔木树种多样性与遥感影像光谱异质性之间的关系。然而,本研究仅采用最简单的神经网络模型对城市乔木树种多样性与遥感影像光谱异质性之间的关系开展初步地探索。未来建议采用非线性映射能力更强的神经网络,进一步提高遥感反演乔木树种多样性的能力。
基于光谱变异性假说和生产力假说,本研究提出了一种基于遥感技术的城市乔木树种多样性反演方法,能够定量表征城市乔木树种多样性的空间格局,可为城市乔木树种多样性地面调查和城市树种的生态系统服务时空动态的研究提供新的思路和技术手段。城市乔木树种多样性地面调查结果的可信度和调查效率分别受到样本的代表性和抽样方法的直接影响。本研究构建的方法可量化城市乔木树种多样性水平的空间分布,可为地面调查提供分层抽样的依据,有助于提高城市乔木树种多样性地面调查结果的可信度和调查效率。城市乔木树种多样性水平的时空动态是研究其生态系统服务动态的重要基础,该方法可快速量化多期城市乔木树种多样性水平,为城市树种的生态系统服务动态研究提供了必要的技术手段。
