一种基于频率估计的自适应主动控制方法

杨理华， 孙俊忠， 张海鹏， 刘树勇， 杨庆超

(1.海军潜艇学院 动力系，山东 青岛 266199； 2.海军工程大学 动力工程学院，武汉 430033)

隔振是降低水下航行器振动所致辐射噪声的有效手段，主要包括被动隔振和主动控制。前者因安装方便且不消耗外界能量，已在中高频段振动控制方面获得广泛应用，但因参数固定无法适应激励及系统变化，低频控制效果仍不够理想。而主动控制引入次级振源，通过信号叠加能有效控制低频振动，并已应用于精密仪器制造、土木工程抗震、船舶机械等领域[1-2]。

美国新型“海狼”级核潜艇已配备主动控制系统，具有良好的声隐身性能[3]。英国扫雷艇应用浮筏主动吸振技术，也有较好的降噪效果。法国Paulstra Vibrachoc公司研发了一种用于柴油机等大型设备的有源隔振系统。Winberg等[4]还开展了舰船及Collins级潜艇有源隔振项目研究。此外，声与振动研究所、Adelaide大学、海军工程大学、上海交通大学、哈尔滨工程大学等国内外单位均取得了诸多研究成果[5-6]。

主动控制包括作动器技术和控制策略，后者作为该领域热点和难点问题，获得较为广泛的研究。鲁棒控制、最优控制等[7-9]常规策略，对参数稳定系统有较好控制效果。针对时变、时滞等不确定性系统，则可应用具有“预测”功能的自适应控制策略。在振动控制领域，基于最小均方理论的滤波自适应算法(FxLMS)应用较为广泛[10]。Carra等[11-14]基于FxLMS算法、FuLMS算法，开展了矩形铝板结构、压电悬臂梁结构振动、齿轮传动系统有源控制研究，并分析了算法收敛性与控制通道之间关系。Das等[15]提出了一种高效运算的频域FxLMS控制算法。Huang等[16-18]还提出单相关FxLMS、FuLMS等改进算法，并在计算量、执行效率及控制效果等方面进行了详细分析。

然而，上述算法多依赖较为精确的参考信号，一般通过拾取设备基脚振动来反映激励信息，对旋转机械还可通过转速传感器直接获取激励特征。受水下航行器设备安装空间狭窄、封闭等条件限制，安装传感器有时较为困难，加之设备间复杂耦合激励作用，这些方法工程实现较为困难或难以有效拾取激励信息，致使控制效果不够理想。实际上，针对旋转或往复设备所致振动激励，其频谱往往具有孤立线谱特征，这种信号可通过频率估计、数字合成来获取，但估计精度将对系统稳定性和控制效果有直接影响。Hyeon等[19-21]分析了有频率偏差的线谱控制系统稳定性，结果表明1%频率偏差就会严重影响系统控制效果。因此，在参考信号难以有效获取、耦合激励条件下，就必须研究一种能够准确在线识别复杂激励频率信息的方法。目前，对线谱信号频率识别有多种途径[22-24]，张志谊等[25]基于子空间原理设计了频率估计器，并通过带通滤波器构造了参考信号。陈红兵等[26]以锁相环频率自适应陷波理论为基础，开展单频信号幅值、相位及频率在线估计研究。研究表明，基于FFT(Fast Fourier Transformation)变换理论的频率识别及信号合成方法高效准确且适合工程实现，在信号分析、处理等领域已有诸多应用，适合参考信号难以有效获取条件下主动控制策略的设计与研究[27-29]。

为此，本文以传统滤波自适应算法为基础，结合FFT频率估计、数字合成方法设计一种可在线准确识别复杂激励信号频率特征，并合成参考信号的自适应控制算法，并由多体动力学软件建立含有旋转机械设备的隔振系统虚拟样机模型，以隔振系统残差信号为控制目标，通过联合仿真及实验对所提算法的控制效果进行分析和验证。

1 滤波自适应算法

20世纪60年代，Diniz等提出最小均方算法(Least Mean Square,LMS)，并在噪声消除、系统辨识等领域获得广泛应用[30-31]。考虑隔振系统功放、作动器等次级通道影响，需对LMS算法修正才可用于振动控制，单输入单输出(Single-Input-Single-Output ,SISO)隔振系统自适应算法结构，如图1所示。

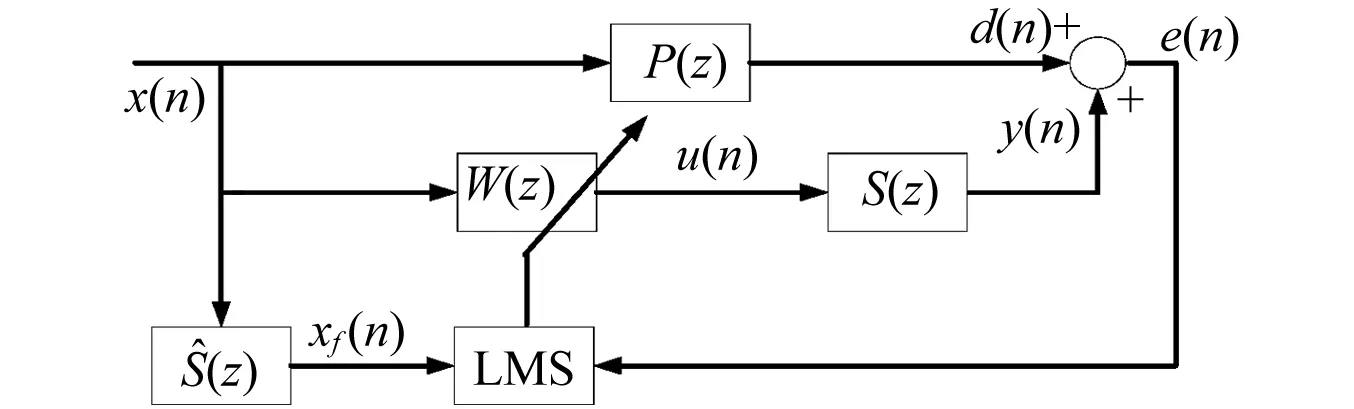
图1 滤波自适应算法结构Fig.1 Filtered-x adaptive algorithm structure

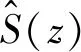
e(n)=d(n)+y(n)

(1)

W(z)为N阶FIR滤波器，u(n)用卷积表示为

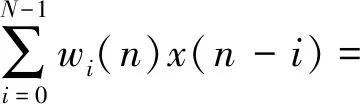
WT(n)X(n)=XT(n)W(n)

(2)

式中：X(n),W(n)分别为滤波器在n时刻参考延时采样序列和滤波器权值矢量

X(n)=[x(n)x(n-1)…x(n-(N-1))]T

(3)

W(n)=[w0(n)w1(n)…wN-1(n)]T

(4)

当S(z)由M阶FIR滤波器代替时，其系数为

S(n)=[s0(n)s1(n)…sM-1(n)]T

(5)

式中：si(n)为n时刻S(z)第i个脉冲响应系数。那么，S(z)输出y(n)可表示为

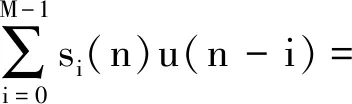
S(n)TU(n)=U(n)TS(n)

(6)

式中：U(n)为W(n)输出u(n)所组成的M×1阶矢量序列

U(n)=[u(n)u(n-1)…u(n-M+1)]T

(7)

联立式(2)，可得S(z)输出y(n)为

y(n)=[XT(n)W(n)]TS(n)=WT(n)X(n)S(n)=

(8)

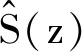
Xf(n)=[xf(n)xf(n-2)…xf(n-N+1)]T

(9)

(10)

以振动残差e(n)为控制目标，定义代价函数为

J(n)=E[e2(n)]

(11)

实际计算中，可用瞬时误差平方e2(n)代替期望值E(e2(n))，式(11)可表示为

(12)

那么，J(n)瞬时梯度可表示为

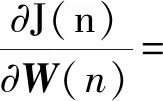
(13)

假设迭代步长较小，滤波器权值系数在较小时间段内更新相对缓慢，则有

(14)

因此，式(13)可改写为

那么，权值迭代系数更新可表示为

W(n+1)=w(n)-μe(n)Xf(n)

(16)

式中：μ为步长系数，对算法收敛速度和控制效果有较大影响，上述滤波自适应算法步骤为：

步骤1拾取初始参考信号x(n)及误差信号e(n)；

步骤2依据式(2)计算控制滤波器输出u(n)；

步骤3依据式(6)计算次级通道响应y(n)；

步骤4依据式(1)、式(10)计算残差e(n)和滤波信号xf(n)；

步骤5依据式(16)更新控制滤波器W(n)。

2 频率估计自适应算法

滤波自适应算法对参考信号x(n)有较高要求，若x(n)难以有效获取时，这种策略的应用及其控制效果就会受到限制。针对旋转或往复机械所致周期性激励，本文将通过频率估计及数字合成的方法来获取估计参考信号，提出一种不需参考信号的自适应控制算法。

2.1 线谱信号频率估计

FFT具有效率高、实时性好、易于硬件实现等优点，在信号分析及处理方面有诸多应用。假设f0(t)是外界连续激励信号，且设初始时刻前有f0(0-)=f0(0)=0，则FFT可表示为

(17)

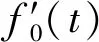
(18)

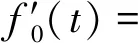
(19)

单位冲击函数δ(t-nT)仅在t=nT时为1，由式(17)和式(19)可得

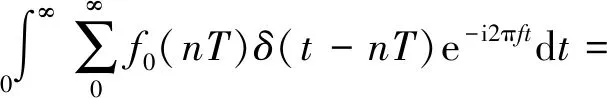
(20)

因δ(t-nT)|t=nT=1,f0(nT)为激励离散值，可用f0(n)表示，则式(20)可以改写为

(21)

式(21)右端为离散信号f0(n)FFT变换，其角频率w与激励频率f、采样频率fs关系为

(22)

式(22)中，该变换将时域f0(n)转化为随w连续变化的频域信号F(eiw)，可反映信号频域分布及变化情况。F(eiw)为响应幅度谱，与激励频率f成线性映射，这就为频率估计提供了必要的条件。若激励为初始相位为零的周期性连续信号，FFT后所识别线谱特征估计幅值为F(eiw)，所对应频率即为估计频率f。然后通过估计幅值、频率即可合成数字信号。若激励为多频信号，还可按幅度谱强度排列幅值及其频率，然后再合成数字信号。实际上，激励信号初相位并非都为零，故合成信号与原始激励往往有所差别，此时还需对相位进行同步估计。但本节所研究频率估计自适应算法仅需准确识别出激励频率信息即可，幅值、相位均可由自适应滤波器自动调整。

2.2 单频估计自适应算法

图2为窄带信号频率估计自适应算法，若已知参考信号频率为ω，则可通过合成信号x0(n),x1(n)及滤波器W(z)输出获得控制信号u(n)，如式(23)、式(24)所示

(23)

u(n)=Bsin(ωt+φ)

(24)

对滤波器响应u(n)进行分解可得

u(n)=B(sinωtcosφ+cosωtsinφ)

(25)

令w0(n)=(B/A)cosφ、w1(n)=(B/A)sinφ，则u(n)可表示为

u(n)=w0(n)x0(n)+w1(n)x1(n)

(26)

图2 单频频率估计的自适应算法Fig.2 Adaptive algorithm of single frequency estimation

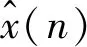
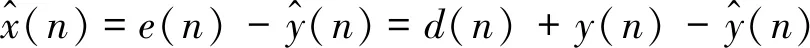
(27)

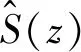
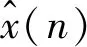
步骤3由式(26)计算滤波器W(z)响应u(n)；

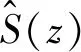
(28)

(29)

步骤5由LMS更新滤波器W(z)权值系数

(30)

因此，频率估计自适应算法重点为频率信息实时准确估计及滤波器W(z)动态更新。图2所示结构仅可控制单根窄带线谱振动，本文将其称为线谱控制器。

2.3 多频估计自适应算法

上述控制算法仅适合单频激励振动主动控制，实际设备振动往往是复杂的多频激励信号。此时，可由多个线谱控制器构造出适合多频激励的频率估计自适应控制算法，具体结构如图3所示。

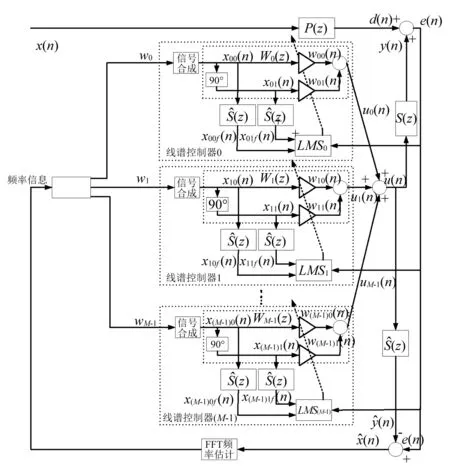
图3 多频估计自适应算法Fig.3 Adaptive algorithm of multi-frequency estimation

(31)

式中：Am,ωm为第m个谐波幅值及频率信息。那么，合成参考可表示为

(32)

式中：M为估计参考信号主要线谱频率成分个数，单个线谱控制器输出为

ui(n)=wi0(n)xi0(n)+wi1(n)xi1(n),i=0,1,…，M-1(33)

式中：wi0，wi1,xi0,xi1分别为第i个线谱控制器权值系数及其正、余弦合成信号。那么，控制器总输出信号u(n)可表示为M个线谱控制器输出叠加

(34)

多频率估计自适应算法步骤与“2.2”节所述相似。

3 联合仿真模型

为验证上述控制算法，以图4、图5所示旋转设备双层隔振平台为研究对象，以残差信号和主动控制力作为评价指标，在忽略扭转、横摇仅考虑垂向运动条件下，通过Adams和Matlab/Simulink联合仿真，对控制效果进行仿真分析。设备转速为1 450±50 r/min，则基频为23.3～25.0 Hz(以24.1 Hz为例)，假设激励由基频及二次、三次谐波组成，相关参数如表1所示。

图4 水泵振动平台虚拟样机Fig.4 Vibration platform virtual prototype of a pump

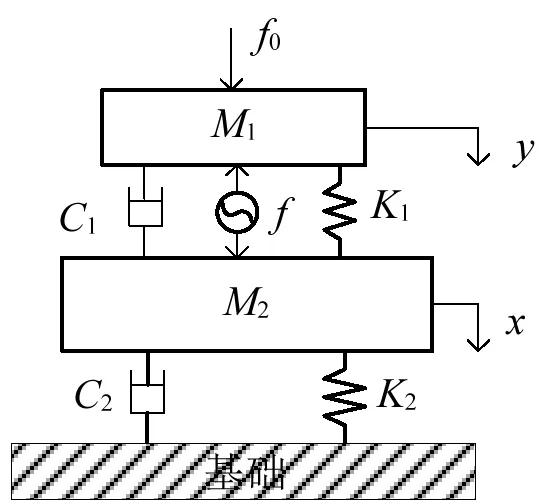
图5 虚拟样机简化模型Fig.5 A simplified model of virtual prototype

表1 双层振动平台参数Tab.1 Double isolation platform parameters

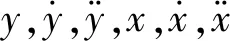
(35)

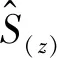
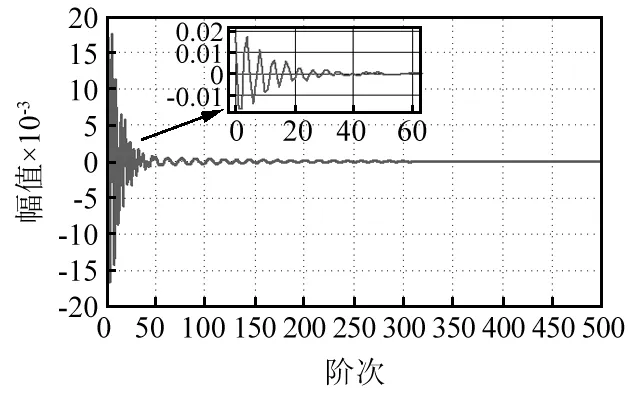
图6 次级通道脉冲响应Fig.6 Secondary path impulse response

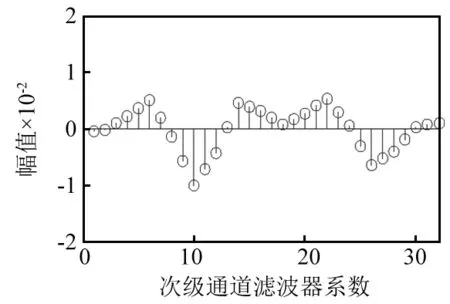
图7 次级通道权值系数Fig.7 Secondary path weighting coefficient

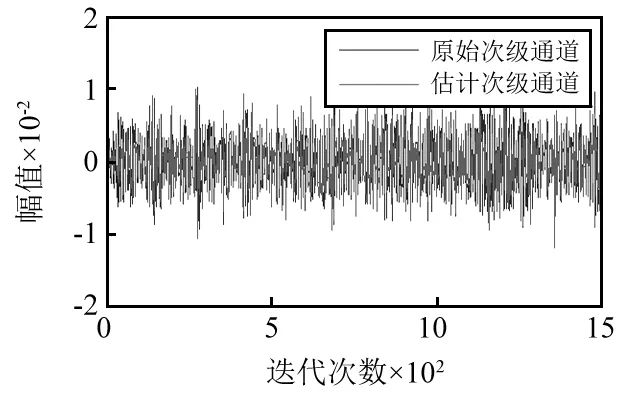
图8 次级通道辨识效果Fig.8 Secondary path identification result

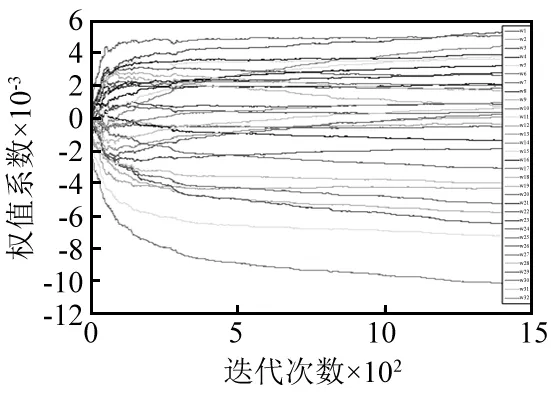
图9 次级通道权值系数Fig.9 Secondary path weighting coefficient

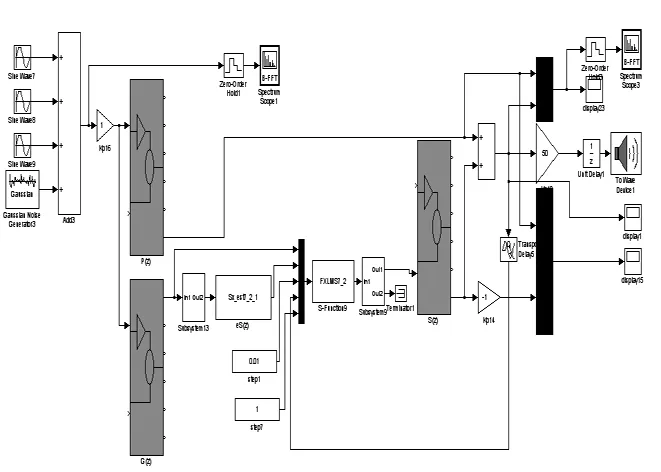
图10 滤波自适应联合仿真Fig.10 Filtered-x adaptive co-simulation

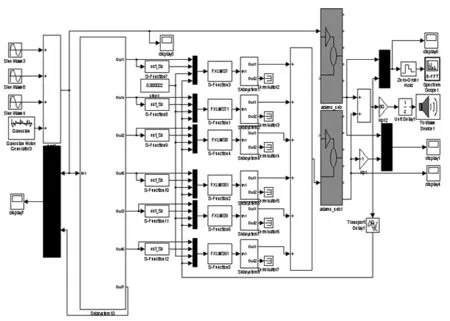
图11频率估计自适应联合仿真Fig.11 Frequency estimation adaptive co-simulation

4 仿真算例

两种算法联合仿真控制效果，如图12～图17所示。其中，图12为FFT频率在线估计效果，图13为原始信号和数字合成信号，图14～图18为多频激励控制效果。

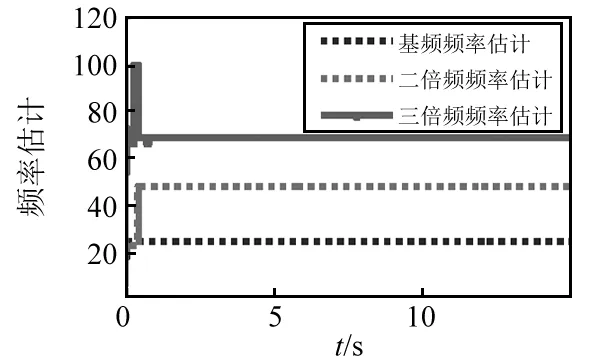
图12 频率估计值Fig.12 Frequency estimation

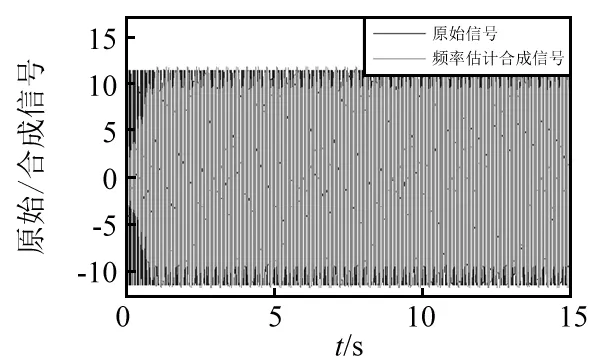
图13 原始及数字合成信号Fig.13 Original and synthesized signal

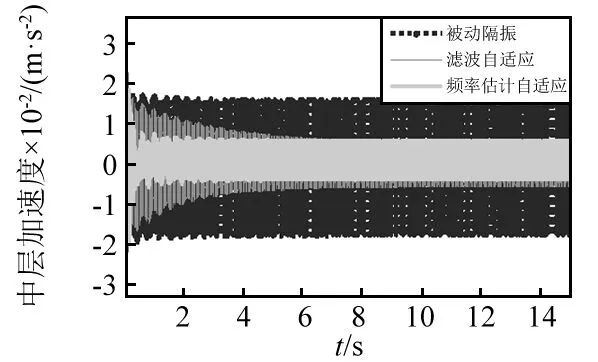
图14 中层加速度Fig.14 Middle acceleration time course

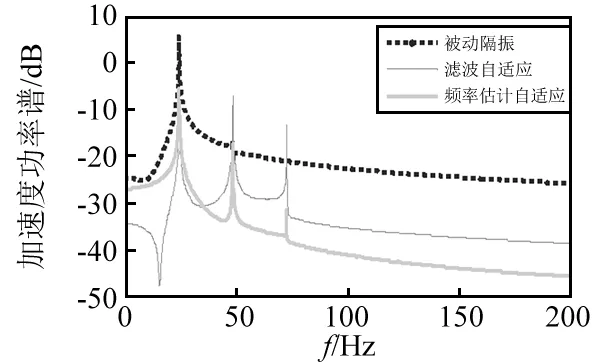
图15 中层加速度功率谱Fig.15 Middle acceleration power spectrum

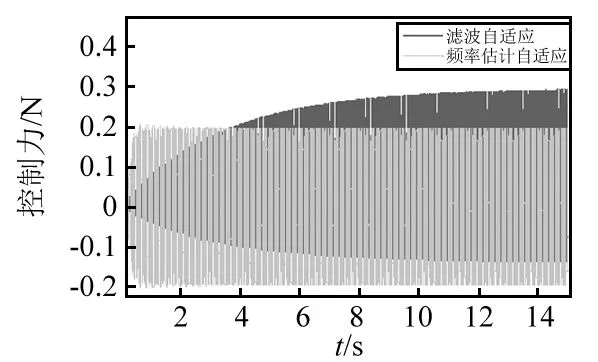
图16 主动控制力Fig.16 Active control time course

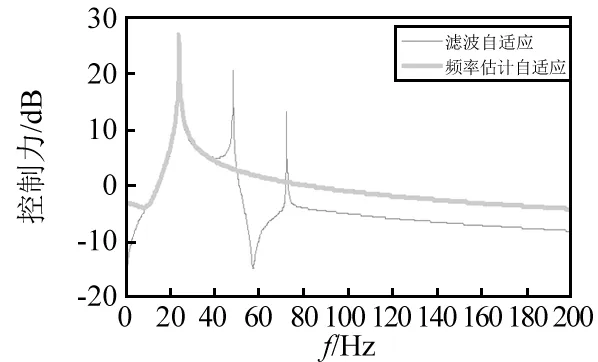
图17 主动控制力功率谱Fig.17 Active control power spectrum

由图12～图17及表2可知，频率估计方法获得频率信息收敛速度较快且准确有效，数字合成信号能获得稳定的估计参考信号。主动控制后两种算法的残差信号和主动控制力收敛速度、控制效果依次增强，都较之被动隔振有明显的控制效果。两种算法窄带线谱分别降低了14.99 dB，-9.66 dB，-7.53 dB及11.1 dB，0.34 dB，10.32 dB，滤波自适应对基频控制效果较好，不足之处是其倍频控制效果较差，而频率估计自适应算法可完全控制基频及谐波，具有多根线谱控制能力。对于基频，本文所提算法主动控制力略有增加；对于倍频，所设计算法仅需较小主动控制力。但两种算法控制力稳态幅值基本相当，这也说明无论哪种方式要抵消同样外界激励，均需要消耗等量的次级振源能量。

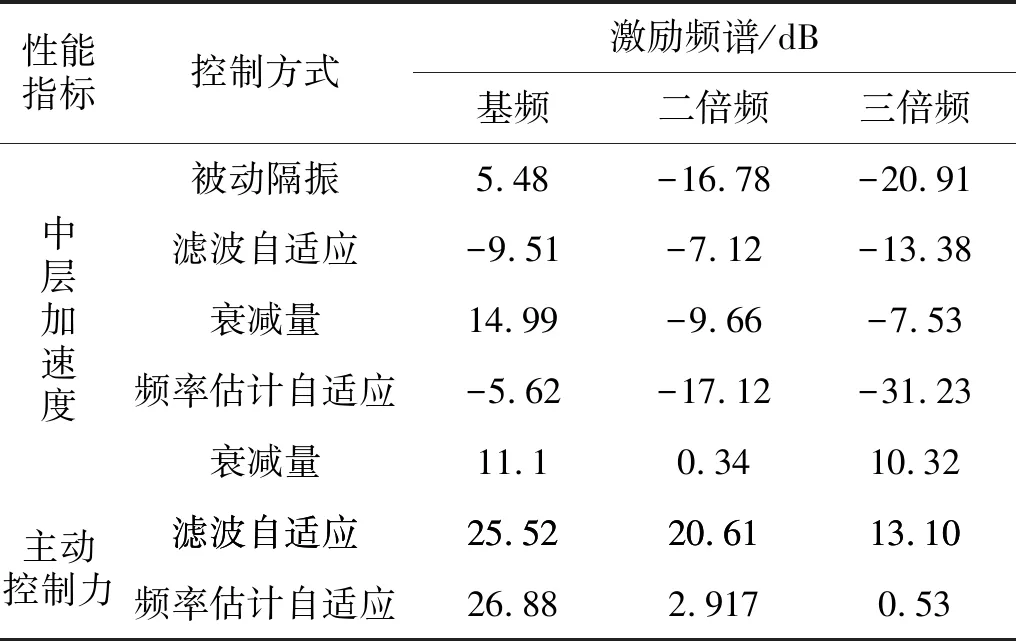
表2 两种控制算法对比Tab.2 Control effect with two algorithms

5 实验研究

试验系统由激振器、双层隔振平台、信号发生器、作动器、NI数据采集仪、DSP控制器、南航FN15150功放、NI上位机监测软件等组成，主动控制实验原理及试验平台如图18、图19所示。

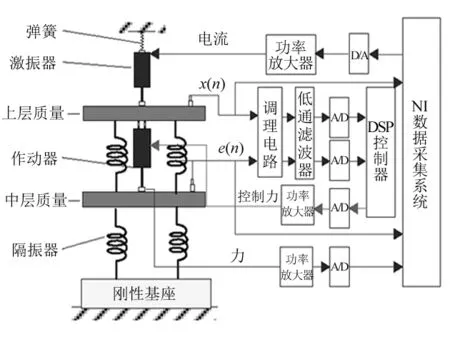
图18 主动控制系统原理Fig.18 The principle of active control system

图19 主动控制试验系统Fig.19 Active control experiments system

考虑水下航行器辅机转速约为1 500～3 000 r/min，则其线谱为25～50 Hz。考虑多振源耦合影响可取单频20 Hz，40 Hz、多频32 Hz+64 Hz+96 Hz作为低频激励信号。采样频率为4.096 kHz，实验中采用巴特沃思低通滤波器对采集信号进行滤波处理。以中层加速度为评价指标，所述算法控制效果如图20～图23及表3所示。

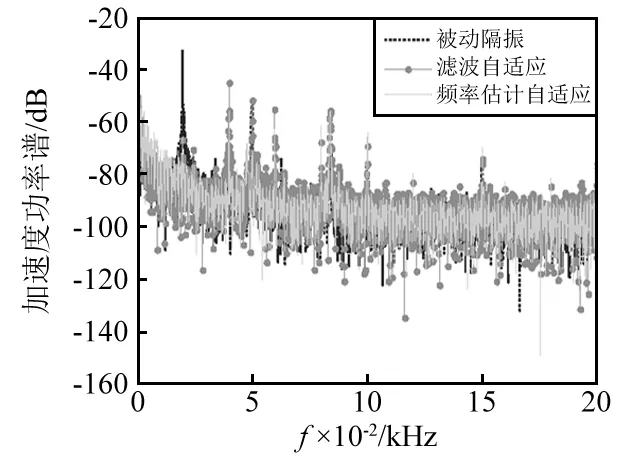
图20 20 Hz激励加速度功率谱Fig.20 Acceleration power spectrum with 20 Hz excitation

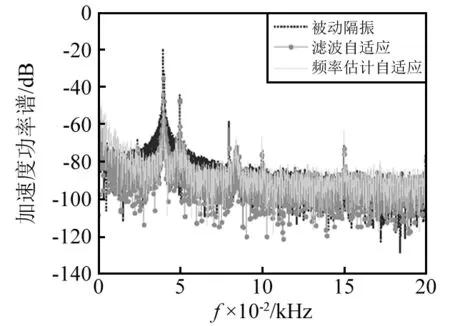
图21 40Hz激励加速度功率谱Fig.21 Acceleration power spectrum with 40 Hz excitation

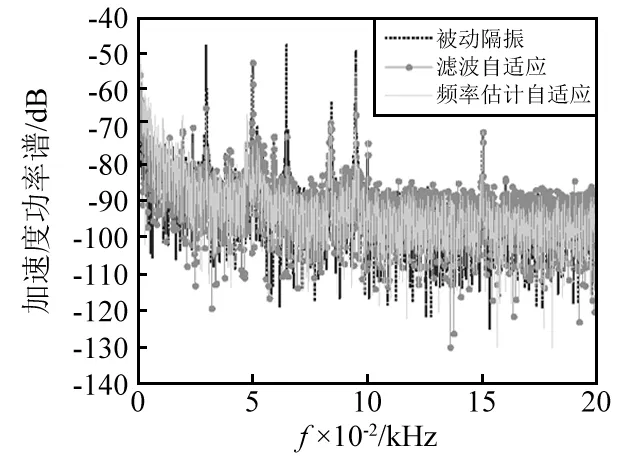
图22 多频激励加速度功率谱Fig.22 Acceleration power spectrum with multi-frequency excitation

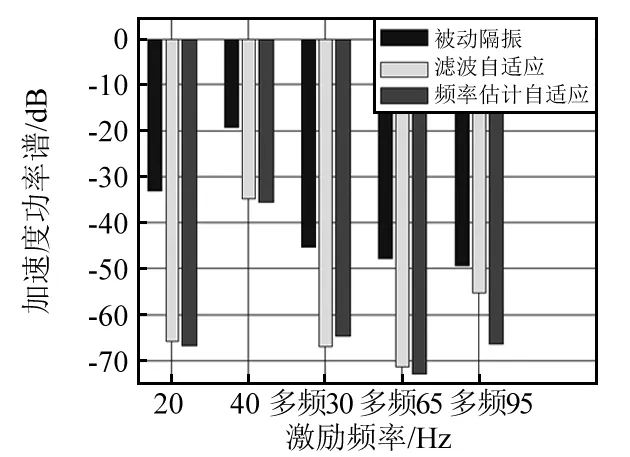
图23 两种算法控制效果Fig.23 Control effect with two algorithms

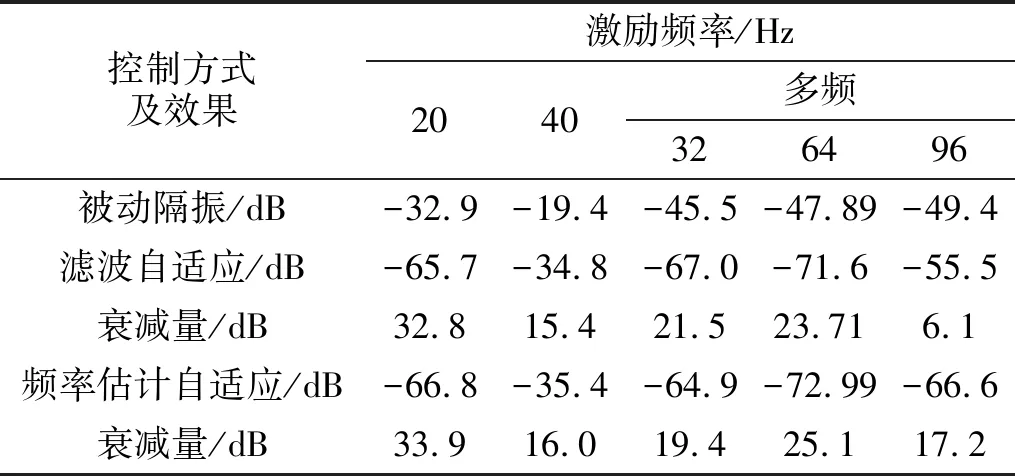
表3 两种算法控制效果对比Tab.3 Control effect with two algorithms

由图22～图25及表3可知，对于20 Hz，40 Hz单频激励，两种方式均有较好效果，分别获得32.8 dB，15.4 dB和33.9 dB，16.0 dB隔振效果，故主动控制较被动隔振有明显的优越性，而且后者还提高了1.1 dB，0.6 dB，这说本文所提算法能够通过频率估计和数字合成为系统控制提供有效的参考信号，而且效果优于滤波自适应算法。对于多频激励，两种算法在各频点降低21.5 dB，23.71 dB，6.1 dB和19.4 dB，25.1 dB，17.2 dB，这说明对于稳态系统两种算法均能有效控制多频激励，后者还提高了-2.1 dB，1.39 dB和11.1 dB，故改进算法谐波线谱具有更好的控制效果。此外，由于次级通道离线辨识模型包含频段有限，虽可有效控制激励线谱却激发出其它线谱信号，但后者相对较弱。但从宽频段来看主动控制后总振级及线谱振动获得明显抑制，且本文所提控制算法效果优于滤波自适应算法。

6 结 论

受水下航行器空间结构及复杂激励影响，往往难以有效获取高信噪比激励信息，致使依赖参考信号的滤波自适应算法工程应用受到限制。对此，本文针对旋转机械所致周期振动，提出一种通过频率估计、数字合成在线获取估计参考信号的自适应控制方法，并以某型旋转设备隔振平台为研究对象，通过联合仿真及实验对所述算法的控制效果进行验证和分析。结果表明：

(1)两种方式主动控制效果明显，且本文所提算法能够通过频率估计和数字合成为系统控制提供准确、有效的参考信号，控制效果也优于滤波自适应算法，该方法可应用于水下航行器辅机设备复杂安装环境下的振动主动控制。

(2)滤波自适应算法对基频控制效果较好，而本文所提算法多根谐波线谱控制能力更强，且其激发它线谱能力相对较弱，从宽频段来看后者具有更好的控制效果。两种算法主动控制力稳态幅值基本相当，这说明无论那种控制方式要抵消相同外界激励，均需要消耗等量次级振源能量。

(3)此外，通过虚拟样机和控制算法开展软件交互式联合仿真，也为控制算法前期仿真分析提供了一种可靠的技术手段。