磨介球对小麦麸皮振动冲击破碎性能的影响

程 敏， 刘保国， 刘彦旭

(1. 河南工业大学 小麦和玉米深加工国家工程实验室，郑州 450001； 2. 河南工业大学 机电工程学院，郑州 450001)

小麦麸皮富含蛋白质、膳食纤维、维生素、淀粉酶系、矿物质等营养成分，在医疗保健、食品加工、生物化工等方面具有良好的应用前景[1]。利用超微粉碎技术对小麦麸皮进行细胞级粉碎已成为其深度开发利用的重要途径[2]。但由于小麦麸皮各结构层纤维含量较高，物理特性表现出韧性大、脆性小的特点，常规粮食粉碎设备很难对其进行超微粉碎加工。鉴于振动磨机在效率上比普通磨机高10～20倍，在速度上比常规球磨机快很多，在能耗上比普通球磨机低数倍，在粒度上能够保证10～25 μm以下，同时由于磨机的冲击、剪切、摩擦等粉碎机理比较适合高纤维物料的加工等优点[3-4]，可以认为振动磨机是小麦麸皮超微粉碎较为理想的设备。黄晟等[5]、Luo等[6]利用振动磨机对小麦麸皮进行了超微粉碎，分别研究了超微粉碎对麸皮理化特性以及制品的影响。

利用振动磨机对物料进行粉碎作业主要涉及振动磨机的振动特性、能耗规律以及物料的破碎性能等三个基本科学问题。其中，破碎性能直接制约振动磨机的工作效率和产品质量，是人们最为关注的问题[7]。从20世纪40年代开始，国内外学者围绕影响振动磨机破碎性能的因素进行了大量的理论与实验研究[8]。研究结果表明在振动特性优化的前提下，磨筒内磨介的运动特性是影响振动磨机破碎性能的关键因素。20世纪80年代中后期以来，德国学者Kurrer等[9]、国内学者王树林[10]、苏乾益等[11]、尹忠俊等[12]、唐果宁等[13]分别采用高速摄像技术观测了不同型号的振动磨机磨介的运动情况，研究发现磨介在磨筒内产生抛射运动、整体回转和本身自转等三种运动形式。这三种运动形式使得磨介之间产生冲击、剪切、挤压、摩擦等多种破碎形式。然而，利用高速摄像技术无法捕捉磨介之间因相互碰撞而产生的接触力以接触变形情况，不能直接评价磨介对物料破碎性能的影响，一般采用宏观粉碎实验从间接方面进行研究和评价。

随着计算机技术的快速发展，利用有限元数值模拟方法探索物料的破碎规律成为一种可能。由于物料的破碎过程具有典型的大变形、瞬态性、突变性等非线性特征，利用非线性有限元数值模拟软件具有显著优势。其中，LS-DYNA是目前公认的最优秀的一款以显式为主、隐式为辅的非线性有限元数值模拟软件，已在众多领域的物料破碎性能数值模拟方面得到应用，如谷物[14]、煤炭[15]、建材[16]等领域。目前，利用LS-DYNA模拟物料的冲击破碎性能，一般采用二维或三维的两构件单边冲击计算模型，将其中一个构件考虑成靶体，另外一个考虑成弹体。但这种计算模型不能模拟磨介对物料的剪切、挤压、摩擦等双边共同作用的破碎形式，进而不能完整描述振动磨机的物料破碎机理。

本文主要探索振动磨机球形磨介对小麦麸皮冲击破碎性能的影响规律。根据磨介球在振动磨筒内的运动形态提出了一种类型三明治的“磨介-小麦麸皮-磨介”的双边冲击计算模型，克服了常见的单边冲击模型无法模拟冲击剪切的不足。选取磨介球与麸皮间的接触力(也即冲击力)以及麸皮接触变形为观测指标，利用LS-DYNA模拟分析磨介球的运动特性(冲击速度、冲击角等参数)、质量特性(密度、直径等参数)以及破碎形式(偏心距)对麸皮破碎性能的影响。研究结果表明磨介球对麸皮破碎性能的影响是显著的，在进行超微粉碎时应科学选择磨介球的运动特性参数和质量特性参数，合理调节小麦麸皮和磨介球的填充量谋划适合麸皮的破碎形式。

1 计算模型及参数设置

1.1 计算模型

在建立小麦麸皮的仿真计算模型时特做如下假设：①将单颗磨介球考虑成刚体，将磨介球质量集中在球心；②将磨介球与麸皮看成是充分均匀混合的，也即磨介球之间均匀填充麸皮；③将单颗磨介球的抛射运动和自转看成径向运动，将单颗磨介球绕公转轨道的公转和自转看成周向运动，忽略磨介球间抛射运动和公转的相互耦合作用，认为二者之间是相互独立的。通过上述假设，选取两颗磨介球、一片麸皮，根据相似原理可得类似三明治的“磨介-小麦麸皮-磨介”的三构件双边冲击计算模型，如图1所示。其中，v1，α，ω1分别为磨介球1的冲击速度、冲击角和自转角速度；v2，β，ω2分别为磨介球2的冲击速度、冲击角和自转角速度；e为磨介球1、2的偏心距；s1，s2为麸皮到磨介球1、2的距离；R1，R2为磨介球1、2的半径，同一级配时R1=R2。以磨介球1的几何中心O1为原点建立直角坐标系XO1Y。限于LS-DYNA的局限性，数值模拟时可根据运动相对性原理将磨介球2进行固定，只给定磨介球1的运动参数。显然，利用该模型仍可以模拟冲击、挤压、剪切、摩擦等破碎形式。

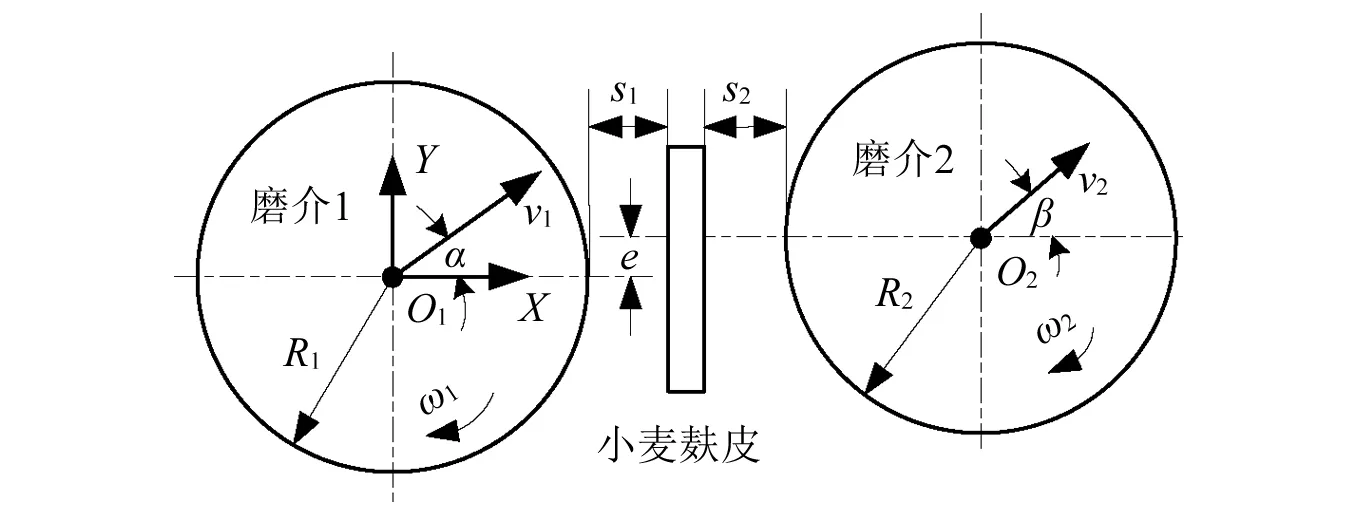
图1 小麦麸皮冲击破碎的仿真计算模型Fig.1 Simulation model of impact crushing for wheat bran

本文主要讨论磨介球运动特性、质量特性、破碎形式对麸皮冲击破碎性能的影响，暂不讨论摩擦效应对麸皮破碎性能的影响，故令ω1=0。建立有限元模型时，考虑到麸皮冲击实验常见的破而不碎现象(有些纤维未完全断裂)，选择板壳单元shell163，长度选择3 mm、宽度选择2 mm、厚度选择80 μm(游标卡尺测量结果)；麸皮的应力-应变过程分为弹性形变和塑性形变两个阶段，材料模型选择双线性Bkin模型。磨介球采用实体单元solid164，半径选择2 mm(分析直径影响特性除外)；由于磨介球的杨氏模量远远大于麸皮的杨氏模量，材料模型选择Rigid刚体模型。s1,s2均取0.5 mm；磨介球之间无偏心(分析破碎形式的影响除外)。麸皮采用四边形映射网格、磨介球采用六面体映射网格进行离散，有限元模型如图2所示。麸皮单元数为3 600，磨介球的单元数为16 384。

图2 小麦麸皮冲击破碎的有限元模型Fig.2 Finite element model of impact crushing for wheat bran

1.2 材料参数

小麦麸皮力学特性与水分含量、温度的关系密切。

陈中伟[17]、Antoine等[18]、Hemery等[19]、Greffeuille等[20]国内外学者分别利用动态热机械分析仪(DMA)测出了小麦麸皮在水分含量13%、温度25 ℃时的应力-应变特性曲线。本文选择Hemery的实验结果作为计算数据，其弹性应变、弹性应力、杨氏模量、极限应变、极限应力等数据如表1第2行所示。Bkin模型需要输入的参数包括：弹性模量、密度、泊松比、屈服应力、切线模量。其中，屈服应力σs约等于弹性应力σela，即σs≈1.26×107N/m2，泊松比取0.3，切线模量Ep=(σmax-σela)/(εmax-εela) =1.96×108N/m2。小麦麸皮的真密度采用基于气体法的实验测量方法及装置进行确定，将另撰文报道。经过多次测量并取均值，麸皮密度ρ≈1 270 kg/m3。磨介球刚体模型需要输入的参数包括：密度、杨氏模量、泊松比。为了讨论磨介球质量特性对麸皮破碎性能的影响，选取氧化锆球、中性玻璃球、耐磨钢球作为磨介，材料参数如表1第3～5列所示。根据表1所示磨介球和麸皮的杨氏模量可知，将磨介球考虑成刚体模型是合理的。

表1 小麦麸皮与磨介球的材料特性参数Tab.1 Material characteristic parameters of wheat bran and grinding ball

1.3 求解设置

求解时，限制磨介球2的移动、转动等全部自由度。磨介球1的冲击速度及冲击角可以通过定义X，Y方向速度分量的方法进行设置。麸皮与磨介球的接触类型采用自动面-面接触。动、静摩擦因数分别取0.3(与氧化锆球、玻璃球接触)、0.4(与耐磨钢球接触)[21]。小麦麸皮边界条件设置为中心结点沿X方向运动，四周无固定，与实际情况相似。由于小麦麸皮在冲击破碎过程中将会产生大变形、甚至出现网格畸变，采用沙漏控制(0.1)和自适应网格控制。为保证计算精度和收敛速度，小麦麸皮积分点选择5个。

2 计算结果与讨论

2.1 磨介球运动特性对破碎性能的影响

2.1.1冲击速度大小的影响

根据文献[22]，选取直径为4 mm的氧化锆磨介球，暂不考虑偏心距和冲击角的影响(令e=0 mm，α=0°)，分别考察冲击速度为0.5 m/s，1.5 m/s，3 m/s，5 m/s时对小麦麸皮破碎性能的影响。选取麸皮与磨介球之间的接触力和接触变形作为考察指标。如果选择麸皮中心单元的Von Mises应力和有效塑性应变作为考察指标，发现当冲击速度增大到一定程度时(如5 m/s)，这两个指标值却发生下降，主要原因可能是麸皮接触区域已经发生破碎，不便于比较分析。图3给出了麸皮在冲击过程中冲击速度对接触力以及接触时间的影响，图4给出了冲击速度对麸皮接触区域及变形的影响。

图3 冲击速度对接触力和接触时间的影响Fig.3 Influence of impact velocity on contact force and contact time

根据图3可知，随着磨介球冲击速度的增大，麸皮与磨介球之间的最大接触力随之增大，从开始接触到最终脱离接触所经历的接触时间却随之下降，与实际情况相符，且与李艳焕等研究中所述的接触时间变化规律一致。说明本文建立的计算模型是可靠的。根据Hertz接触理论可知，磨介球与麸皮之间的接触区域呈圆形，且接触区域的半径近似为[23]

(1)

注：括号内t是指磨介球与麸皮发生冲击后开始脱离接触的时刻，下同图4 冲击速度对麸皮接触变形的影响Fig.4 Influence of impact velocity on contact deformation of wheat bran

根据图4可知，随着冲击速度的增大，麸皮接触区域亦随之增大，与Hertz接触理论相符。在磨介球的冲击作用下，麸皮首先发生弹性变形，然后发生弹塑性变形，当变形超过应变极限时出现破碎，最后麸皮与磨介球脱离接触时发生弹性恢复。当速度为0.5 m/s时接触区域中心部位网格出现滑移收缩现象；当速度为1.5 m/s时接触区域中心部位网格出现扭曲重叠现象，但未出现破碎；当速度为3 m/s时接触区域中心部位开始出现大变形，网格发生畸变，麸皮发生破碎；当速度为5 m/s时接触区域进一步增大，压碎由中心向四周扩散，破碎面积增大。由此可知在1.5～3 m/s存在一个临界破碎速度，经计算该临界速度约为2.5 m/s，此时临界接触力约为10 N左右，大约在图1所示两条曲线的交点处。为了提高麸皮的破碎性能，应在振动磨机外部动力条件许可的情况下提高磨介球的冲击速度，增大接触力，这与杨小兰等研究中所得结论一致。

2.1.2冲击角的影响

仍选择直径为4 mm的耐磨钢球，不考虑偏心距的影响(令e=0 mm)，冲击速度为3 m/s，分析冲击角α分别为0°，15°，30°，45°时对麸皮破碎性能的影响。图5、图6分别给出了冲击角对麸皮接触力、接触时间和接触变形的影响情况。

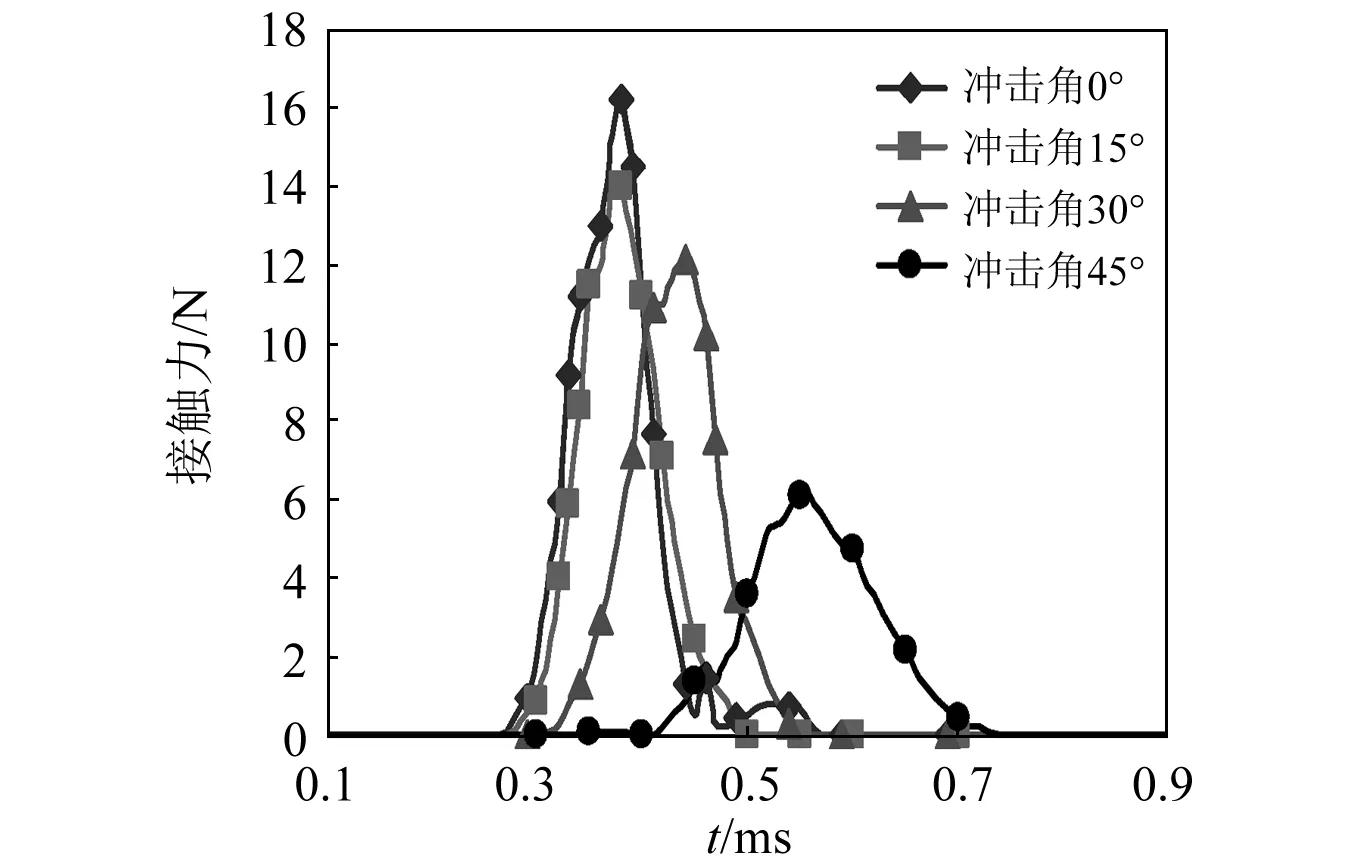
图5 冲击角对麸皮接触力的影响Fig.5 Influence of impact angle on contact force of wheat bran

图6 冲击角对麸皮接触变形的影响Fig.6 Influence of impact angle on contact deformation of wheat bran

根据图5可知，随着冲击角的增大，磨介球与麸皮之间的接触力逐渐减小，接触开始的时间向后推移，整体接触时间逐渐增长，说明冲击角的存在对麸皮破碎性能的影响是不利的。当α=45°时，接触力小于10 N，麸皮未出现破碎，如图6(d)所示。主要原因在于冲击速度在X方向的分量减小，正向冲击动量减小，影响麸皮与磨介球之间的接触力。至于接触时间的变化，主要与麸皮Y方向速度分量有关系。冲击角越大，Y方向速度分量越大，接触开始的时间越晚，达到最大接触力的时间越长，接触结束的时间也越晚，导致有效接触时间增长，这与实际情况也相符。

根据图6可知，随着冲击角的增大，麸皮接触区域逐渐变小，直至消失。由于接触力随着冲击角的增大而减小，麸皮破碎情况由严重变形(压碎)到一般变形(滑移收缩)。冲击角越大，出现滑移收缩现象的麸皮网格越多，如图6(d)所示；冲击角越小，基本未出现滑移收缩变形就已发生压碎，如图6(a)所示。总之，冲击角的存在不利于麸皮的破碎，一般可通过增大磨介球与麸皮的填充量来减小冲击角。

2.2 磨介球质量特性对破碎性能的影响

2.2.1 磨介球密度的影响

分别选择直径为4 mm的中性玻璃球、氧化锆球、耐磨钢球，讨论磨介球密度对麸皮破碎性能的影响，具体密度参数见表1，冲击速度设置为3 m/s。图7给出了三种不同密度的磨介球与麸皮之间的接触力。图8给出了磨介球密度对麸皮接触变形的影响。

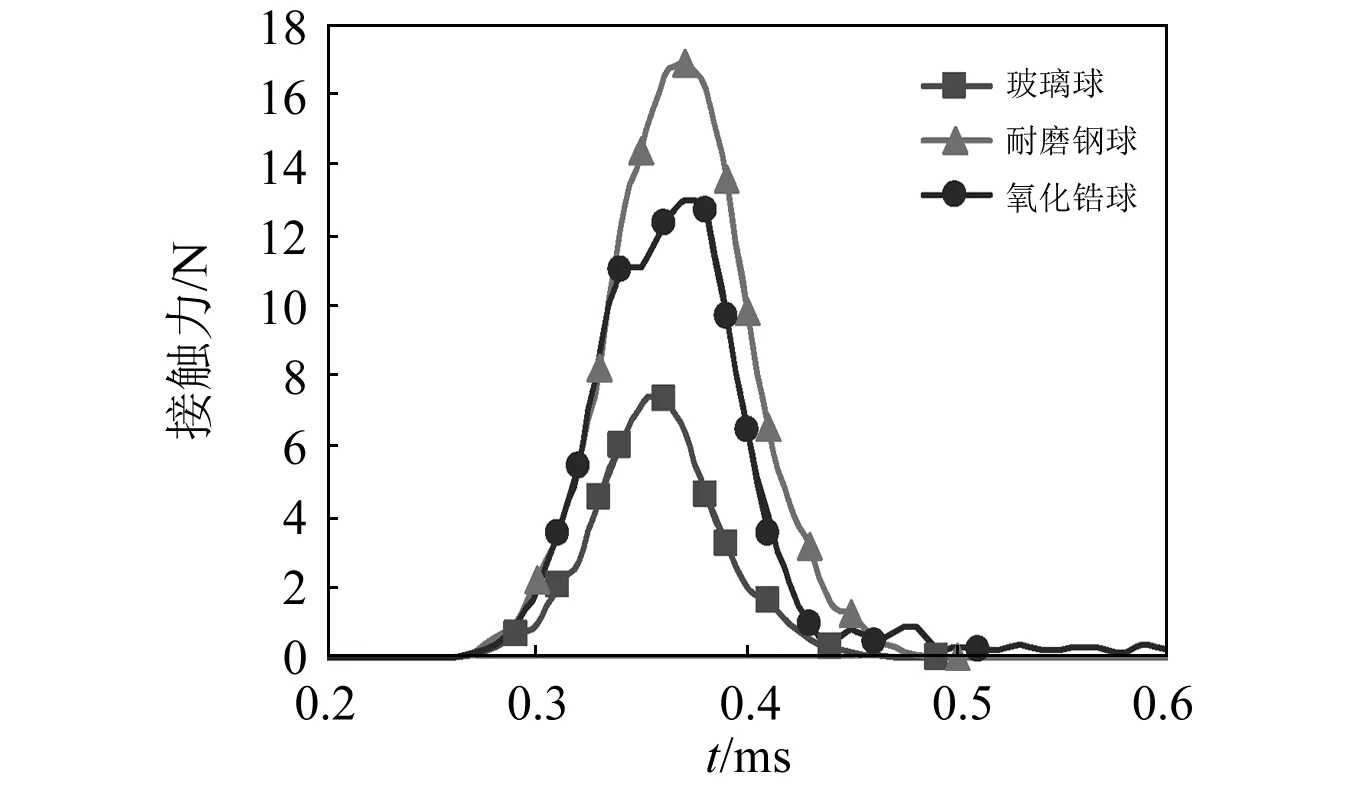
图7 磨介球密度对麸皮接触力的影响Fig.7 Influence of grinding ball density on the contact force of wheat bran

图8 磨介球密度对麸皮接触变形的影响(t=0.5 ms)Fig.8 Influence of grinding ball density on the contact deformation of wheat bran(t=0.5 ms)

图7表明随着磨介球密度的增大，麸皮与磨介球之间的接触力逐渐增大，接触时间基本相同。根据图7可得玻璃球、氧化锆球、耐磨钢球的冲量之比约为0.43∶0.81∶1，动量变化之比约为0.33∶0.73∶1(假设塑性碰撞)，近似满足动量定理。由于玻璃球密度较小，接触力小于10 N，麸皮未发生破碎，如图8所示，而由于氧化锆和耐磨钢球的接触力均大于10 N，麸皮均发生了破碎。图8表明在相同运动条件下高密度磨介球接触变形区域更大，更有利于麸皮的破碎，主要原因在于磨介球的密度越大，质量越大，动能越大，致使麸皮与磨介球之间的破碎能也越大，因此耐磨钢球的破碎效果优于氧化锆球和玻璃球。以上分析表明，在麸皮粉碎过程中应向粉碎腔内添加高密度的磨介球。

2.2.2 磨介球直径的影响

根据杨小兰等的研究，选择直径为4 mm，6 mm，8 mm，10 mm的耐磨钢球，冲击速度设置为3 m/s，探讨磨介球直径对麸皮破碎性能的影响。图9、图10分别给出磨介球的直径对接触力和麸皮接触变形的影响。

图9 磨介球直径对接触力的影响Fig.9 Influence of grinding ball diameter on contact force

图10 磨介球直径对麸皮接触变形的影响Fig.10 Influence of grinding ball diameter on contact deformation of wheat bran

根据图9可知，磨介球的直径越大，麸皮与磨介球之间的接触力越大，但接触时间也越长，而不是随着接触力的增大而变短，不利于麸皮的冲击性破碎，主要原因在于过大的冲击力导致麸皮与磨介球之间产生粘着现象，同时随着磨介球直径的增大，磨介球与麸皮之间的接触面积增大，二者界面间的毛细力也逐渐增大，增长了麸皮的弹性恢复时间。以上原因导致图9所示的接触力波峰出现削平现象，导致接触时间增长，从而降低磨介球与麸皮之间的碰撞频率。根据图9可知，四种直径磨介球的冲量之比约为0.077∶0.239∶0.462∶1，动量之比约为0.064∶0.216∶0.512∶1，也近似满足动量定理。图10表明随着磨介球直径的增大，接触变形区域随之增大。经计算可知，四种直径磨介球接触变形区域占比分别为5.97%，23.85%，42.42%，66.27%。根据式(1)可知，这与接触力和磨介球直径都有关系。在相同接触深度下，直径越大，接触面积越大。随着磨介球直径的增大会造成磨筒内磨介球数量的减小，也会降低麸皮与磨介球之间的接触概率。因此，单纯依靠增大磨介球直径来提高麸皮的破碎性能并不经济，这会造成磨介球因过大接触力而产生变形，加剧磨损。一般先采用大直径磨介球对大尺寸麸皮进行破碎，使麸皮表面产生大量裂纹，如图10(c)、图10(d)所示，然后再利用小直径磨介球进行冲击，使麸皮表面裂纹扩展，发生断裂，也即应采取合适的磨介级配制度，提高振动磨机的破碎性能。

2.3 磨介球破碎形式对破碎性能的影响

根据图1可知，当α=0°，e=0 mm时，磨介球1、2之间产生对心碰撞，使麸皮具有冲击挤压效应；当α=0°，e≠0 mm时，磨介球1、2之间产生偏心碰撞，使麸皮具有冲击剪切效应。为了分析因偏心距而引起的冲击挤压、冲击剪切破碎形式对麸皮破碎性能的影响，选取直径为4 mm的氧化锆球进行冲击计算，冲击速度设置为3 m/s，偏心距分别选取0 mm，0.2 mm，0.4 mm，0.6 mm。图11给出了不同偏心距时麸皮与磨介球之间的接触力以及接触时间的变化情况。图12给出了偏心距对麸皮接触变形情况的影响。

图11 偏心距对麸皮接触力的影响Fig.11 Influence of eccentricity on contact force of wheat bran

根据图11可知，随着偏心距的增大，麸皮与磨介球之间的接触力基本保持不变，接触时间也基本相同。经计算可知，不同偏心距时的冲击剪切接触力比冲击挤压力分别高7.46%，5.07%，3.66%。单从接触力来看，冲击剪切比冲击挤压更有利于麸皮的破碎。但表现在接触变形方面的影响可忽略不计，如图12所示。接触圆的大小基本相同，破碎变形也基本相同。如果选取麸皮中心单元应变作为考察指标，可以作出麸皮中心单元有效塑性应变与偏心距之间的关系，如图13所示。

图12 偏心距对麸皮接触变形的影响Fig.12 Influence of eccentricity on contact deformation of wheat bran

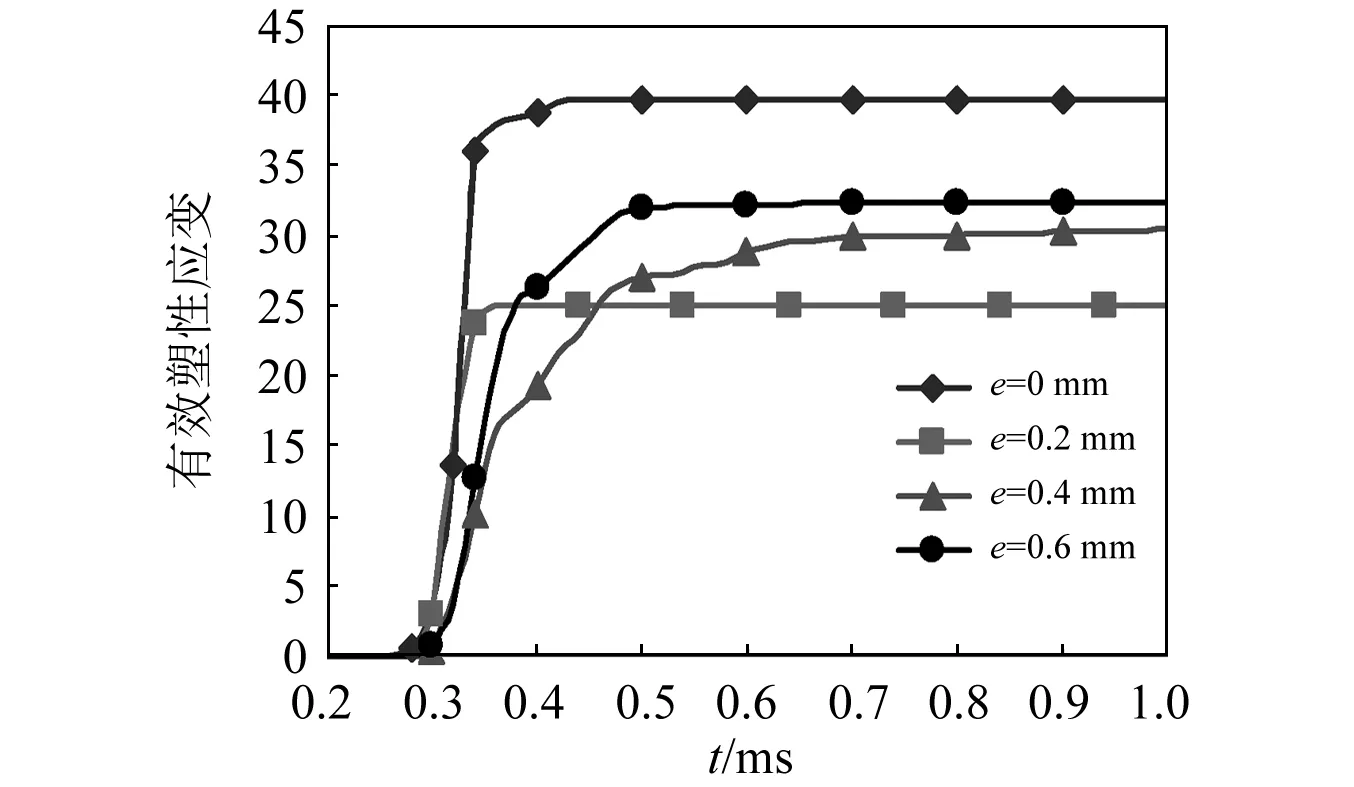
图13 偏心距对麸皮中心单元应变的影响Fig.13 Influence of eccentricity on strain of wheat bran center unit

根据图13可知，当偏心距为零时，麸皮几何中心处单元的有效塑性应变最大，此时冲击挤压破坏占据优势。随着偏心距的增大，麸皮中心附近的单元有效塑性应变逐渐增大，说明冲击剪切破坏起主导作用。但总体来说，冲击挤压应变大于冲击剪切应变。这与文献[24]所得结论一致。这是因为随着偏心距的增大，承担接触力的单元增多，导致麸皮单元最大有效塑性应变值降低。这就是脆性物料选择冲击粉碎的原因。因此，对于大尺寸麸皮应以冲击挤压为主，增大破碎变形程度；对于小尺寸麸皮应以冲击剪切为主，增大接触力，剪断麸皮中的纤维。因此，在粉碎大尺寸麸皮时，应增大麸皮与磨介球的填充量，增大冲击挤压的发生概率。当麸皮尺寸较小时，可以降低麸皮与磨介球的填充量，增大冲击剪切的发生概率。

3 结 论

本文基于“磨介-小麦麸皮-磨介”双边冲击计算模型，利用LS-DYNA软件数值模拟分析了磨介球对麸皮振动冲击破碎性能的影响，得到如下结论：

(1)与单边冲击计算模型相比，“磨介-小麦麸皮-磨介”双边冲击计算模型不仅可以模拟冲击挤压，还可以模拟冲击剪切，且数值模拟结果与单边冲击计算模型以及其他方法的研究结论一致，说明双边冲击计算模型是正确的、可靠的。

(2)磨介球对小麦麸皮破碎性能的影响是显著的。冲击速度越大，破碎性能越好；冲击角越大，破碎性能越差。密度参数越大，破碎性能越好；直径越大，接触力越大，接触变形也越大，但接触次数降低。偏心距对冲击挤压和冲击剪切的接触力、接触区域的影响较小，冲击挤压产生的有效塑性应变大于冲击剪切的有效塑性应变，对于大尺寸麸皮应以冲击挤压为主，对于小尺寸麸皮应以冲击剪切为主。

(3)本文的研究思路和方法也为研究小麦麸皮的自身状态、物理特性以及粉碎环境对其破碎性能的影响提供一条新的途径，将另撰文阐述。