轴心轨迹测量中圆弧形导致的偏差及其修正方法
2019-12-31马会防
马会防, 万 召
(中国航发商用航空发动机有限责任公司,上海 200241)
通过两个相互垂直的位移传感器,可以对转子进行轴心轨迹的测量。轴心轨迹的分析,在水泵[1-2]、发电机[3-5]、机床[6]等多种旋转设备均有应用,基于对轴心轨迹分析所得到的特征,可判断设备的运行状态;特别是在故障诊断方面,关于轴心轨迹的研究成果非常丰富,例如,基于轴心轨迹的转子升速过程故障特征提取[7],基于轴心轨迹形态的转子裂纹故障分析[8],基于轴心轨迹自动辨识高速主轴系统的故障等等,这些研究表明轴心轨迹在旋转设备中已有广泛而重要的应用。
近些年来来,随着我国大力发展航空发动机,轴心轨迹在航空发动领域中的应用也日益深入与广泛。文献[9-14]在系统动特性、载荷下的响应、系统稳定性等方面应用到轴心轨迹,文献[15-16]将轴心轨迹引入到指尖封严与泄漏特性的研究中,文献[17]结合航空发动机转子对轴心轨迹的提纯进行了研究,文献[18]在分析静偏心对挤压油膜阻尼器减振特性的影响时,从轴心轨迹方面进行了研究,文献[19-20]在进行发动机旋转叶片-机匣碰摩、轴承座松动等研究时,也进行了轴心轨迹的分析,文献[21]则基于叶尖间隙测量系统的轴心轨迹测量技术进行了探讨。
航空发动相关的轴心轨迹测量,需要结合结构具体特点进行研究,例如,研究挤压油膜厚度的动态变化时,可在挤压油膜阻尼器中进行轴心轨迹测量,由于油膜半径间隙一般在0.1~0.25 mm,即径向上位移范围为±0.25 mm,范围较小,因此对轴心轨迹的测量精度较高,需要尽可能地减少测量误差;再如,研究叶片断裂飞脱的试验中,径向上位移范围较大,这在种情况下,如何测得较为精确的轴心轨迹,值得深入研究,已有文献中对该方面的研究较少,文献[22]仅涉及到轴心轨迹的提纯,而非对轴心轨迹直接提高测量精确度的研究。
为满足越来越高的测试要求,进一步提高轴心轨迹的测量精度,本文分析了测试截面上转子圆弧形对测试结果的影响,探讨了测量截面上的转子半径R以及径向位移对测量精度的影响,研究表明,测量截面上的转子半径越小、径向位移越大,则测量值与实际值偏差就越大。在对测量偏差进行分析的基础上,提出了一种测量偏差的修正方法,给出了修正计算公式,该方法需要输入测试截面的转子半径,然后基于测得的位移可计算实际的轴心位移,可以消除圆弧导致的测量偏差,在一定程度上提高测量精度。
该方法简单,实用性强,即可用于实时测量系统,也可用于测量后的数据处理中,具有重要的实际工程应用价值,对于提高振动测量精度等方面具有重要的参考价值。
1 偏差分析
1.1 偏差产生的原因
轴心轨迹的测量,一般选取转子某个截面,在截面上布置两个相互垂直的位移传感器,开始采集后,每一个数据采集时刻都可以从两个传感器分别获取一个位移值,将该组位移值绘制在平面上,形成轴心轨迹的一个点,下一个采集时刻,形成轴心轨迹的下一个点。
假设某个时刻,转子轴心只在一个方向上产生了位移,如图1所示,转子轴心由O点水平移动到O’点,在X方向(水平方向)的位移为|OO’|=x,测量值与实际位移值一致;转子轴心在Y方向上未发生位移,但是,Y方向上的位移传感器会测得一个位移值y,显然,y属于测量偏差。同样,如果仅在Y方向上产生轴心位移时,则在X方向上会产生一个位移测量偏差值。

图1 测量偏差示意图Fig.1 Sketch for measurement deviation
由图1可知,产生测量偏差的原因在于被测截面是个圆弧形,由于测点位置是固定的,当转子轴心在一个方向上移动时,必然在另一个方向上引起测量偏差。
图1只是轴心位置的一个特例,当轴心位置不在图示的坐标轴上时,轴心位移测量值并不等于轴心的实际位移值,两个传感器的测量值都含有一定的偏差量,测量值是真实位移值与偏差值的叠加值,下面将采用MATLAB仿真计算对旋转过程中产生的偏差进行更为详细的说明与描述。
MATLAB对转子进动时轴心轨迹的仿真计算模型,如图2所示,转子以偏心半径e进行圆形进动,转子截面半径R,设位移传感器布置在坐标轴的正半轴上,两传感器测得的位移值分别为x,y,显然x,y是圆心坐标(x0,y0)的函数,其关系式为
(1)
式中:x0=ecos(θ);y0=esin(θ)。
由式(1)可根据圆心坐标(x0,y0)得到测量值x,y。

图2 MATLAB仿真模型示意图Fig.2 Sketch for MATLAB simulation model
x,y构成的轴心轨迹中包含有测量偏差的轴心轨迹。根据该MATLAB仿真模型进行计算,可以模拟出测量得到的轴心轨迹,例如,偏心距e=1 mm、转子截面半径R=3 mm时,x,y的仿真结果如图3所示。

图3 MATLAB模拟的轴心轨迹测量结果Fig.3 Results of measurement on axis orbit from MATLAB simulation
由图3可知:(1)当一个通道的测量值达到最大时,该通道此时的测量偏差最小;(2)当一个通道的测量值达到最大时,另一个通道此时的测量偏差最大。
将上述的x,y,绘制成轴心轨迹,如图4所示。

图4 x与y构成的轴心轨迹Fig.4 Axis orbit of x and y
由图4可知,轴心轨迹在第一、第三象限的测量偏差较大,当然,这与传感器的布置位置有关系,如果传感器不是布置在0°,90°,而是布置在90°,180°,则测量偏差将在第二、第四象限较大。
1.2 偏差大小的量化分析
由“1.1”节可知轴心轨迹产生测量偏差的原因,但未知这种偏差对测量结果的影响具体有多大,本节将尝试量化分析偏差的大小。
图1所示情形——在X方向的位移测量值不含有测量偏差量,而在Y方向上的测量值恰恰全部为偏差量,非常适合于进行偏差的量化分析与研究。
结合图1,图中所示偏差量y可以表示为y=|AB|=|AO|-|BO|,图中测试截面上的圆半径为R,即|BO’|=|AO|=R,可得
(2)
式中:y为偏差量的绝对值,为考察偏差量的相对大小,以y/x的百分比表示偏差量的相对值。
根据工程中常见的转子位移幅值范围,取X方向上的位移x具体范围值为0.05~2 mm,取常见的转子半径R为10~200 mm,根据式(1)可计算(x,y),x∈(0.05,2),y∈(0.05,2),R∈(10,200)范围内y/x的百分比,如图5所示。

图5 y/x百分比曲面Fig.5 Surface of y/x percentage
由图5可知:(1)X方向位移值的大小,位移值x越大,Y方向测量的偏差相对值就越大,近似于一种线性增加;(2)测量截面圆半径的大小,圆半径R越小,测量偏差相对值就越大,非线性增加,圆半径R较小时,增加很快;(3)位移值与测量截面圆半径的联合影响,当圆半径R较小,且位移值较大时,测量偏差相对值很大(可达10%量级);当圆半径R较大,且位移值较小时,测量偏差相对值较小。
根据上述分析,在工程应用中,我们可以:
(1)采用式(1)对测量偏差的大小进行评估;
(2)为减少测量偏差,在径向跳动都满足测量精度要求的各转子截面中,尽可能地将测量截面选择在转子截面半径较大处;
(3)对测量精度要求高的情况下,有必要对测量值进行修正。
2 偏差的修正
2.1 修正方法
由“1.2”节可知在一定情况下,轴心轨迹的测量偏差较大,需要进行修正,以消除修这种圆弧形导致的测量偏差。
修正方法与原理(见图6),当转子轴心由O点运动到O’点时,在X方向上的测量值为x,其实际位移值为x0,同样,在Y方向的测量值为y,其实际位移为y0。如果求出x0与y0,则求出了转子轴心的实际位移。
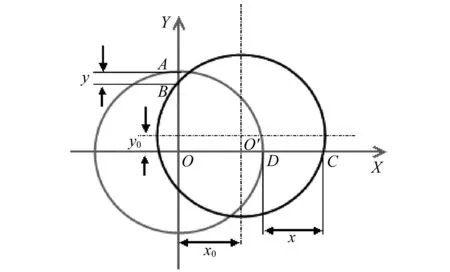
图6 修正方法解释用图Fig.6 Explanation for modification method
在坐标系XYO中,圆O’的中心坐标为(x0,y0),它与坐标轴交于B点和C点,两点坐标分别为(0,R+y)、(R+x,0),则将两点坐标代入圆O’的方程,可得方程组
(3)
解方程组可得,解一
(4)
解二
(5)
从数学上讲,式(3)方程组的确存在两组解,解不唯一,如图7所示,圆O’与圆O’’均是方程组的解,两圆都通过点B、点C,且半径均为R。
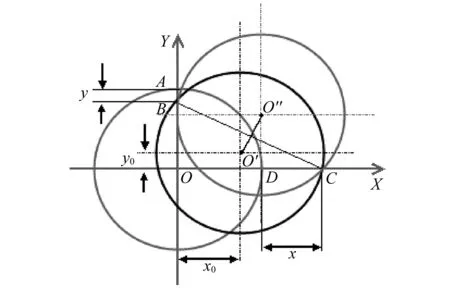
图7 式(3)方程组的两个解Fig.7 Two solutions for equation group(3)
分析解二的表达式可知,x0,y0分别由两项相加而得,若忽略带有根号的第二项,则x0,y0分别为(R+x)/2,(R+y)/2,x0,y0的值可达到R的量级,而一般情况下的位移值较小,即测试截面半径R远大于位移测量值x,y以及修正后的位移值x0,y0,因此可以排除解二的可能;但在位移值与R量级接近的特殊情况下,需要谨慎考虑解二的可能性。
由公式可知,在轴心轨迹测量的ti时刻,根据ti时刻测得的X方向、Y方向的测量值xi,yi,及时计算出实际轴心位移值x0i,y0i,所以,轴心轨迹的修正方法可在实时测量系统中对轴心轨迹进行实时修正。当然也可以先采集、存储数据,获得数据后再进行后处理以修正数据。
2.2 修正方法的验证
由于“2.1”节中采用理论推导的方法得到修正公式,这种情况下很难再采用理论方法证明公式的正确性,但可以采用实例计算进行一次验证。
前面“1.1”节中的轴心轨迹数据含有圆弧形导致的偏差,可用“2.1”节中的数据修正方法进行修正。以X轴为起始点,逆时针方向为顺序,对轴心轨迹上的各点依次利用“2.1”节解一中的式(4),进行数据的修正。修正前后的轴心轨迹对比如图8所示。

图8 修正前后轴心轨迹对比Fig.8 Axis orbits before and after being modified
由图8可知修正后的数据圆度明显得到改善。
前面“1.1”节中的轴心轨迹理论上是半径为1 mm的一个圆,修正后的轴心轨迹上各点的x,y与其对应的理论值相减,可得到x,y在各处的偏差量,如图9所示。
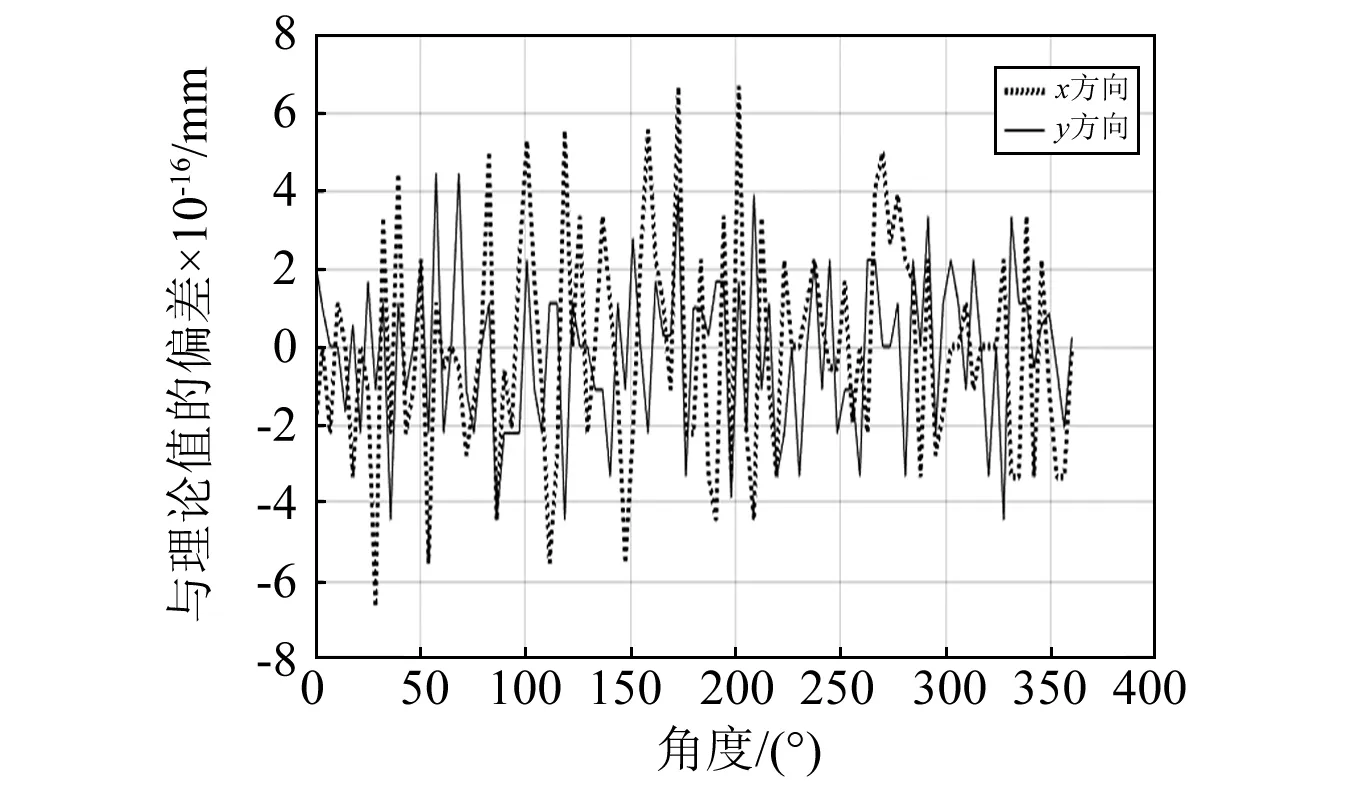
图9 修正值与理论值的偏差量Fig.9 Deviation between modified data and theoretical data
修正后的数据与理论值偏差在10-15mm以内,偏差非常小,修正方法可以消除圆弧形导致的测量偏差。
2.3 工程应用
某转子轴心轨迹测量截面上的圆半径R为20 mm,该测试对测试结果精度要求较高,需要对测得的轴心轨迹进行修正,以消除圆弧形测量截面引起的偏差。
运用“2.1”节解一中的式(4),对X,Y方向上各时刻的位移测量数据依次、逐点进行修正,修正前后的时域数据对比如图10所示。
由修改前后的X,Y方向的时域数据图可知,在各峰值处测量偏差变小,这与图1中所示的情形是相应的,图10中的峰值对应于图1所示的轴心轨迹在坐标轴上的情景,此时,测量值接近实际位移值。
修正前后的轴心轨迹如图11所示。

图10 修正前后XY方向的时域数据Fig.10 Time field data in X and Y direction before and after being modified

图11 修正前后的轴心轨迹Fig.11 Axis orbits before and after being modified
轴心轨迹在第一、第三象限得到较大量的修正。
3 结 论
首先,本文分析了转子轴心轨迹测量中圆弧形导致的测量偏差,以及偏差的大小与截面半径、径向位移的关系;其次,提出了偏差的修正方法,该方法计算公式简单,容易理解,便于应用,可用于实时测量系统,也可用于后处理程序中,最后,提供了一个轴心轨迹修正的实例。
本文解决了轴心轨迹测量中圆弧面导致的偏差问题,有利于提高测量结果精度,具有很强的工程实际应用价值。
