随机车辆荷载下大跨钢桥伸缩缝纵向位移响应及病害控制研究

韩大章， 郭 彤， 黄灵宇， 刘中祥

(1. 中设设计集团股份有限公司，南京 210005； 2. 东南大学 土木工程学院，南京 210096)

桥梁伸缩缝是设置在梁端与桥台或梁段间的伸缩装置，主要用于调节车辆荷载、温度等引起的梁体纵向运动和变形以及防止地震中的梁体碰撞等[1- 2]。作为桥梁上部结构的连接部件，伸缩缝的性能不仅直接影响着行车的安全与舒适性，还关系着桥梁整体结构的动力响应。然而，在车辆荷载等反复作用下，伸缩缝往往会因发生过早的损伤而需频繁的维护更换[3]。例如，主跨1 385 m的江阴大桥在1999年建成通车时两端各安装了一个转轴式伸缩缝(最大位移范围为±1 000 mm)，仅4年后纵梁与承载箱连接处就出现了上下滑动支座脱落及纵梁滑板损坏等病害，且经过多次维修后仍不能满足使用要求，故于2007年进行了整体更换[4]。近年来频现的损伤案例表明：伸缩缝是桥梁结构中的易损部件之一，而大跨钢桥由于柔性大，对振动较为敏感，其伸缩缝病害更为突出，故对其在运营状态下的真实性能还有待更深入的研究。此外，桥梁伸缩缝病害的维护不仅昂贵(往往会花费20%以上的维护费用[5])，而且会造成交通中断、结构功能退化等间接影响。因此，桥梁伸缩缝的病害问题引起了国内外广大学者的关注。

正常运营状态下，桥梁伸缩缝受到车辆荷载的竖向冲击和水平作用。对于伸缩缝的车致竖向冲击振动响应及病害，目前国内外学者已进行了深入地研究[6-9]，分析了伸缩缝的抗冲击性能、伸缩缝致跳车对结构的影响、伸缩缝的疲劳寿命以及车辆经过时伸缩缝噪声的产生机理和传递特征等，同时在有关伸缩缝设计和试验的规范中给出了设计、制作及安装的指南[10- 11]。然而，以往有关桥梁伸缩缝纵向运动的研究多侧重于超限位移损伤的机理、极端荷载下纵向响应分析等方面，忽视了纵向位移的累积效应，并不能有效揭示反复车辆荷载作用下桥梁伸缩缝纵向运动所致病害的机理，且鲜有涉及此类病害控制的分析。此外，大跨桥梁中大型伸缩缝的滑动支承往往采用PTFE材料，其滑动失效寿命往往只有20 km。因此，累积位移的研究以及控制变得尤为重要。

为控制大跨钢桥的伸缩缝病害，本文以润扬悬索桥为工程背景，结合随机车辆荷载模型和桥梁有限元分析，建立了一种随机车流下伸缩缝位移响应的分析方法，分析了车速、车致振动频率、车流量和重型车对伸缩缝纵向位移的影响，并研究了所提出的车流限速和增设梁端阻尼器的措施控制伸缩缝病害的效果。

1 桥梁概况及伸缩缝病害

1.1 桥梁概况

润扬悬索桥[12]是主跨为1 490 m的双塔双索面悬索桥。主梁为单箱单室扁平流线型全焊钢箱梁(Q345D级钢)，其截面最高为3m，双向六车道的桥面全宽36.3 m(见图1)。该桥两端的引桥和桥塔之间分别并行安装了两个当时世界最大行程(2 160 mm)的模数式伸缩缝[13]。其结构主要包括革命文物两根Z型边钢梁、26根I型中钢梁、纵向支撑梁、位移控制弹簧、滑动支撑、压紧支撑、锚箱等(见图2)。其中边钢梁由锚固件与伸缩缝两侧的桥面板相连，边/中钢梁上翼缘间设置鸟型防水密封胶条(构成伸缩体)；支承梁(多根)穿过中钢梁的吊架嵌入到两侧桥体内的锚固箱中，并与一侧锚固箱相连；吊架与支承梁通过滑动支承和压紧支撑相连，以保证中钢梁能够在支承梁上自由滑动。此外，中钢梁下翼缘间无吊架处间隔设置了位移控制弹簧(橡胶柱)。当车辆通过伸缩缝时，荷载通过中钢梁、滑动支承、位移控制弹簧传递到支承梁上，再通过锚固箱内滑动支承和压紧支承传递至两侧桥体上。与此同时，位移控制弹簧发生剪切变形，将车辆所致纵向位移分配至各单独移动的中钢梁间隙中。

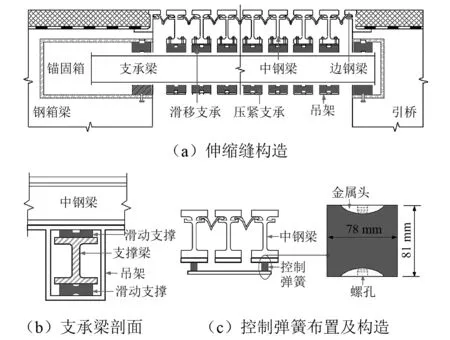
图2 模数式伸缩缝的构造Fig.2 Configuration of modular expansion joint

1.2 伸缩缝病害

润扬悬索桥于2005年建成，然而通车后不久就观测到其伸缩缝有较大的位移。现场调查发现部分滑动支撑和压紧支撑存在严重的磨损、位移控制弹簧出现开裂或顶部螺帽脱落、吊架发生变形等病害(见图3)。2007年对伸缩缝进行了较大的修复，在轴承部位加入了高性能滑动材料并安装了限位带(允许吊架之间的最大相对运动为80 mm)[14]，目前每年仍需要大量维修。2016年的现场调查发现仍存在严重的位移控制弹簧开裂及螺帽脱落等问题，其中与主跨钢箱梁连接处的位移控制弹簧病害尤为严重。此外，靠近引桥的吊架发生了变形，一些限位带也被损坏。

图3 润扬悬索桥伸缩缝典型病害Fig.3 Typical damage of expansion joints in the RSB

2 随机车流下伸缩缝位移响应分析方法

2.1 有限元建模及校对

润扬大桥悬索桥的三维有限元模型如图4所示。其中桥塔采用三维等参梁单元(Beam4单元)模拟；吊索和主缆使用只承拉不受压的三维线弹性杆单元(LINK10单元)模拟，其初始应变由平衡状态下实测索受力计算确定；钢箱梁由Beam4单元组成的脊骨梁模型来模拟，主梁(脊骨)通过垂直于梁的无质量刚性梁与吊索连接。材料特性和实常数(即横截面积，惯性矩等)按设计参数计算获得并分配给相应的单元。为获得较为精确的桥梁纵向位移，采用具有弹簧和阻尼器特性的Combin37单元模拟力-速度非线性特性[15]，如式(1)所示。

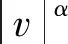
(1)

式中：c为阻尼系数，取值为3 750 kN·(m·s)-α；α为常数指数，α=0.4；ν为阻尼器两端的相对位移速度；sgn(ν)为符号函数，显示阻尼力方向。

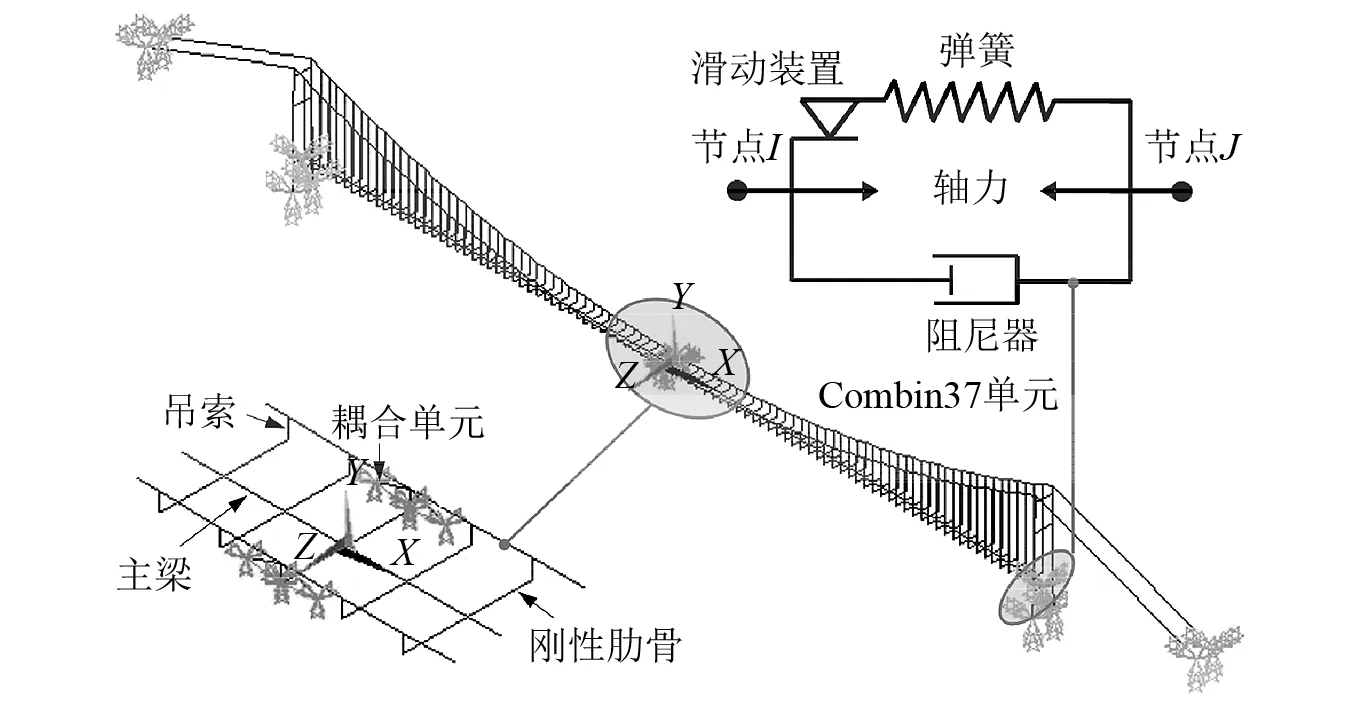
图4 润扬大桥悬索桥有限元模型Fig.4 Finite element model of the RSB

为验证模型的有效性，以模态频率和两个竣工验收工况的实测数据进行了有限元模型校验分析。实测中桥梁的一阶侧弯、一阶竖弯和一阶扭转模态所对应的频率分别为0.058 6 Hz，0.122 1 Hz和0.239 8 Hz。由模态分析可知，这三个主要振型的计算频率分别为0.051 2 Hz，0.126 0 Hz和0.212 1 Hz，与测试值吻合较好。竣工验收时车队静载布置于桥面上引起桥端位移的实测数据如表1所示(扣除温度作用)。该竣工验收工况中车辆荷载均为单车重300 kN的52辆自卸货车。加载车辆均重300 kN，前轴重60 kN，中轴和后轴轴重均为120 kN；车辆的中前轴轴距为3.5 m，中后车轴轴距为1.3 m，前轮距为1.7 m，中后轮距均为2.0 m。这些车辆分成4行13列分布在内车道和中车道，相邻行的中车轴间距16.1 m。其中工况1和工况2中第7列车辆的中车轴到跨中的距离分别为273.7 m和0 m。由表1的分析结果可知，两工况下主梁两端纵向相对位移的计算值也均与测试值吻合较好。这表明所建立的有限元模型能够表征伸缩缝的纵向位移。

2.2 随机车辆模型

为了模拟实际车流，基于高速公路称重收费系统调取的车辆荷载数据和车流监控录像的图像识别技术，建立了随机车辆模型[16]，包括车数、车型、轴数、轴重、车速等分布信息。其中多数轴重分布符合正态或对数正态分布规律[17]，可直接用这两种概率密度函数加以描述；部分轴重分布呈现两峰或多峰的特征，可采用两个或三个正态概率密度函数的加权组合加以表示[18]，如式(2)所示。

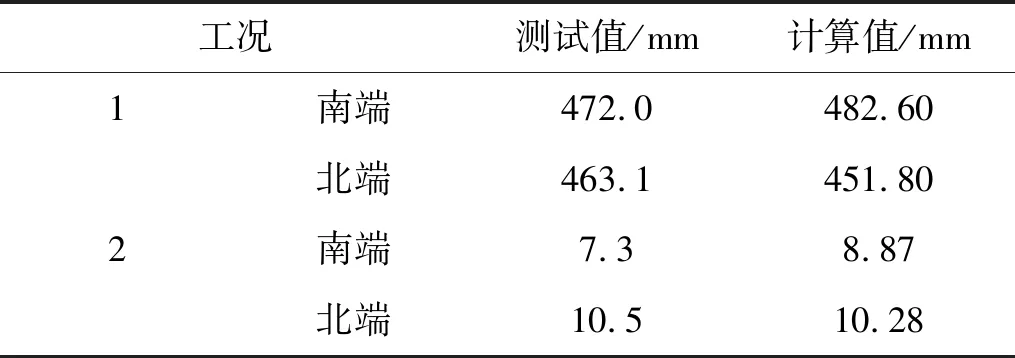
表1 主梁两端顺桥向位移

(2)

式中:f(y|c,w,θ)为混合概率密度函数；fi(y|θi) 为第i个单峰概率密度函数；wi和θi分别为第i个概率密度函数的权重系数和参数。

2.3 随机车流位移响应分析方法

为了定量分析实际车流下伸缩缝的位移响应，本文结合桥梁有限元模型和随机车辆模型提出了一种伸缩缝位移响应分析方法。该方法可结合有限元分析模拟实际车辆荷载下大跨桥梁伸缩缝的位移响应，其具体流程如下：

步骤1基于车辆信息建立随机车辆模型；

步骤2在Matlab中根据随机车辆荷载模型抽样生成的车辆样本集，包括抽样轴重、轴距、车速以及行驶方向等信息；

步骤3通过均匀抽样为每个车辆样本配置上桥时间点，其中时间样本范围为3 600 s(1 h)；

步骤4根据样本上桥时间点、车速、轴距以及荷载步数计算获得每个荷载步下桥梁各节点的加载数据(即车流数据)，当车轴位置没有节点时，将轴重按车轴位置到对应单元两端节点的距离反比例分配到两端节点上；

步骤5将各荷载步的加载数据依次调入有限元模型并进行瞬态动力学分析，提取伸缩缝纵向位移时程并进行后续研究。

3 有限元分析

3.1 车速对伸缩缝的影响

在2011年7月28日—2011年8月31日的35天内，桥梁上通过车辆共计371 167辆，则平均每小时通过润扬桥的车辆数为442辆，平均每侧221辆。以该期间过桥的辆车为样本，结合大桥的车辆收费分类方式以及车辆的轴数特征，将样本车辆分为六种车型，统计分析建立随机车辆模型。该模型六种车型的车辆关键信息如图5所示。由于样本统计时间较长，通过该模型抽样生成的车流量较好地反映了实际交通荷载状况。

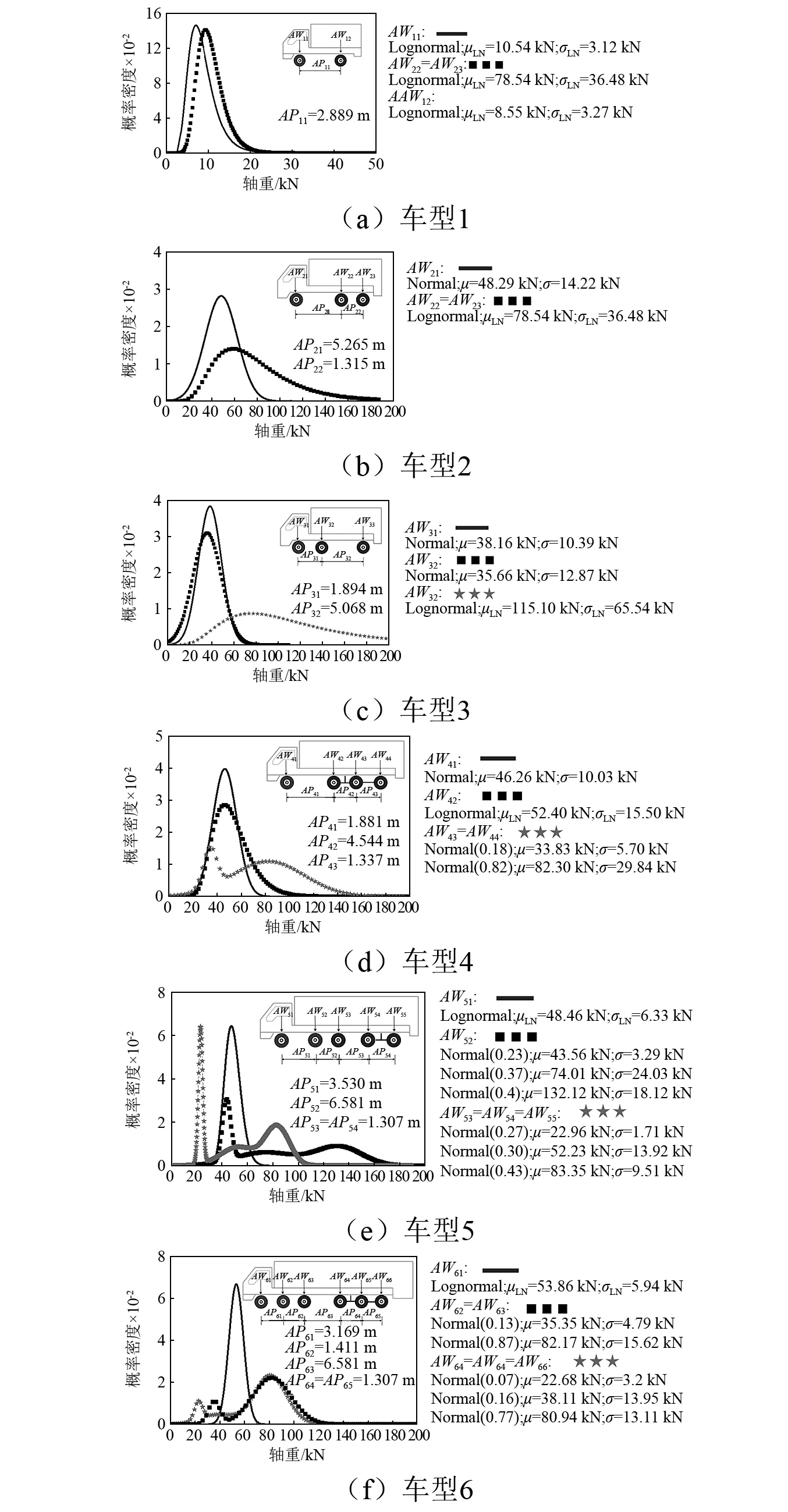
图5 车辆信息模型Fig.5 Vehicle information model

采用该随机车辆模型抽样生成车速分别为100～110 km/h(高速)、70～80 km/h(中速)和30～40 km/h(低速)三个样本集，并分别进行随机车流下伸缩缝位移响应分析。图6(a)给出了高速、中速和低速三种情况下，车流通过润扬大桥时伸缩缝的纵桥向位移时程曲线。对比各位移时程曲线可知，不同车流速度下伸缩缝的纵桥向位移差别较大，高速行驶的车流比低速行驶的车流能够引起伸缩缝产生更多振幅较大的高频振动。因此，高速行驶的车流会导致伸缩缝的累计位移迅速增加。

图6(b)进一步给出了这三种车速下伸缩缝的位移频谱图。总体而言，在低速车流通过时伸缩缝的低频位移量较多，高频位移量较少；在高速车流通过时其高频位移量较多，低频位移量较少。由此可见，高速行驶的车辆会给桥梁带来非常可观的高频振动，使伸缩缝的纵向运动更为显著。此外，三种车速下伸缩缝的位移频谱均在0.045～0.05 Hz，0.08～0.09 Hz和0.115～0.125 Hz这三个频段出现峰值，说明桥梁在这些频段内比较容易发生共振，需要加以避免。

表2所示为由伸缩缝位移时程计算得到的不同车速范围下车流过桥所引起的伸缩缝累计位移。由表2可知，累计位移与伸缩缝高频位移量成正比，高频位移量越多，累计位移越大。当车流由中速提升到高速行驶通过桥梁时，伸缩缝的小时累计位移由2.39 m提升到6.60 m，增长量超过2.7倍。考虑到伸缩缝滑动支承(PTFE材料)的滑动失效寿命的测验值只有20 km，那么中速和高速车流下伸缩缝的有效工作时间将分别约为9.6 年和3.5 年；而滑动支承受损后滑动摩擦因数会急剧增大，导致伸缩缝滑动受阻而无法正常工作，故其寿命可能会更低。由此建议桥梁维护单位应控制车辆过桥的速度，限速范围为70～80 km/h左右，并应限制超速行为。

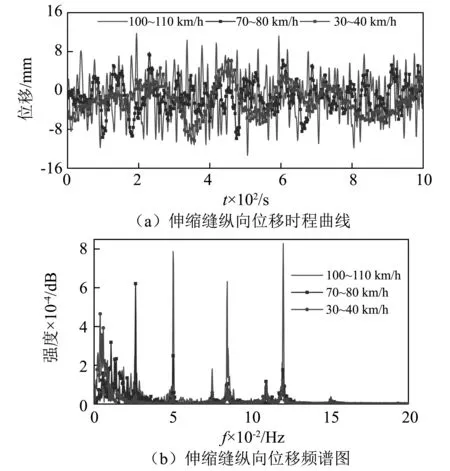
图6 车流以不同车速过桥时伸缩缝纵向位移Fig.6 Longitudinal displacement of expansion joints when vehicle flow crossing bridges at different vehicle speeds

表2 车流以不同车速过桥时伸缩缝纵向累计位移

3.2 极端工况下伸缩缝位移分析

在“3.1”节的有限元模拟中，每小时过桥车辆总数是通过车流量的月平均值计算确定的，故分析所得的结果符合正常运营时的情况(平均水平)。然而，实际状况中往往会出现车流量剧增和车流中重型车比例较大两类极端不利情况。例如，节假日的车流量突增和夜晚小型车较少、重型车较多的情况。图7所示为2011年8月16日各时段车流量的平均值和各车型车辆数占比情况。总体而言，中午时段内过桥的车辆较多，而夜晚时段内过桥的车辆显著减少。对比图7中各车型所占比例可知，白天车辆数较多，但以小车(车型1)为主；晚上车辆数减少，但是主要为重型车(车型5和车型6)。其中1型车在日间8 ∶ 00—20 ∶ 00占比较高，5型和6型车在夜间20 ∶ 00—次日8 ∶ 00占比较高。

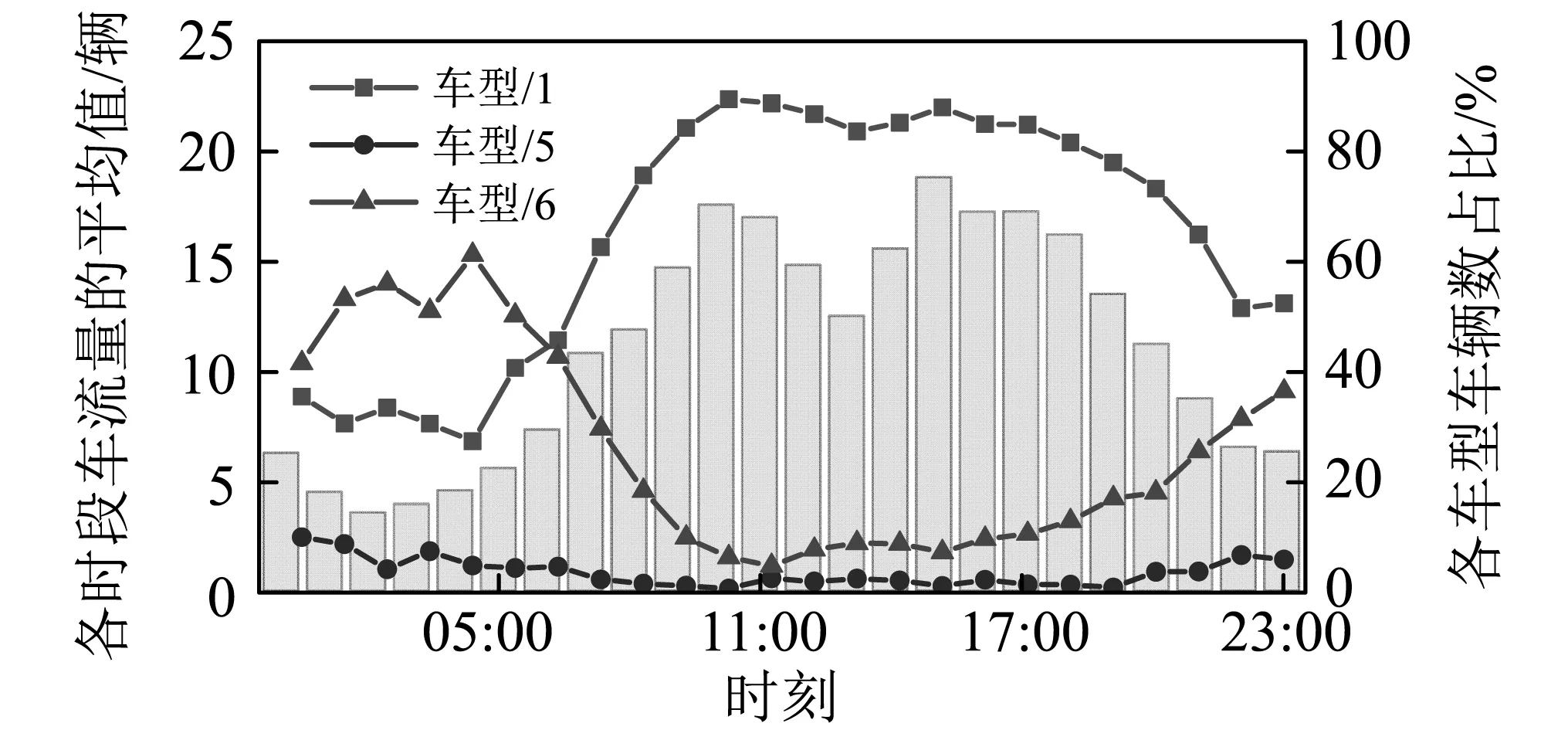
图7 车流情况(2011年8月16日)Fig.7 Information of traffic flow (August 16, 2011)

分别以14 ∶ 00—15 ∶ 00(车流量大)和4 ∶ 00—5 ∶ 00(重型车比例高)的车辆数据为样本，生成随机车流。表3给出了这两个时段的车流量的时平均值和各车型车辆数占比抽样情况。当车辆样本集的车速范围为70～80 km/h时，在上述两种交通状况下伸缩缝的纵向累计位移如表3所示。表3同时展示了“3.1”节平均水平交通状况下的数据，以作为参照。

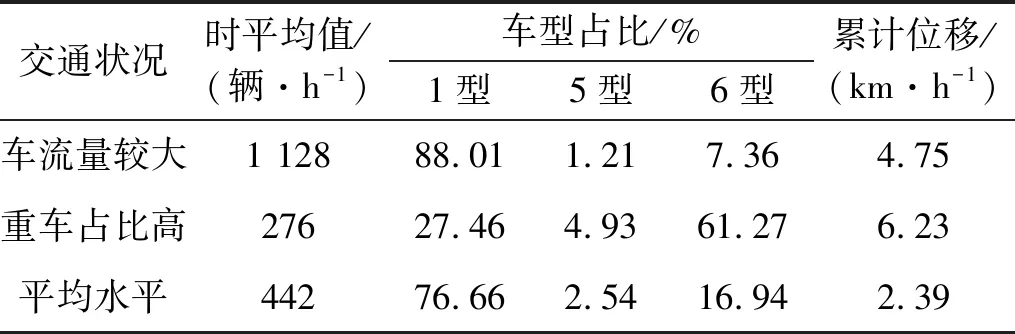
表3 三种交通状况下抽样样本情况及伸缩缝纵向累计位移

可以看出，在车流量较大和重型车比例高这两种较为极端的交通状况下，伸缩缝累计位移都会显著增加。在车流量较大的交通状况下，车辆总数为平均水平的2.5倍，伸缩缝累计位移增加到平时交通状况下的2倍左右。这说明尽管小型车辆重量不大，但由于其数量众多，对桥梁伸缩缝的累计位移量也存在显著影响。此外，在重型车较多的工况中，即使在车辆总数仅为平均水平的一半左右，其伸缩缝累计位移甚至超过了平时情况下的2.5倍。由此可知，重型车(车型5、车型6)的增加会显著增加伸缩缝的累计位移，加剧伸缩缝的病害。因此，在桥梁后期保养中需要重点关注车流量较大和重型车比例高这两种交通状况，优先控制重型车辆的比例、轴重大小及车速，其次在车流高峰期可适当采取限流措施。

此外，图8给出了平均水平和两种极端交通状况下伸缩缝位移频谱。由该图8可知，两种极端交通状况时的伸缩缝位移的强度在大多数频段上都高于其在平均水平交通状况时的强度。对比平均水平交通状况下0.025～0.03 Hz、0.08～0.09 Hz以及0.115～0.125 Hz这三个主要频段的强度发现：这三个频段上的强度在车流量较大的交通状况下均有所增加；而低频段上的强度在重型车比例高的交通状况中却有所下降。这说明车辆数的增加会导致高频位移量的增加，而重型车则容易在后两个高频段内引起桥梁的共振。

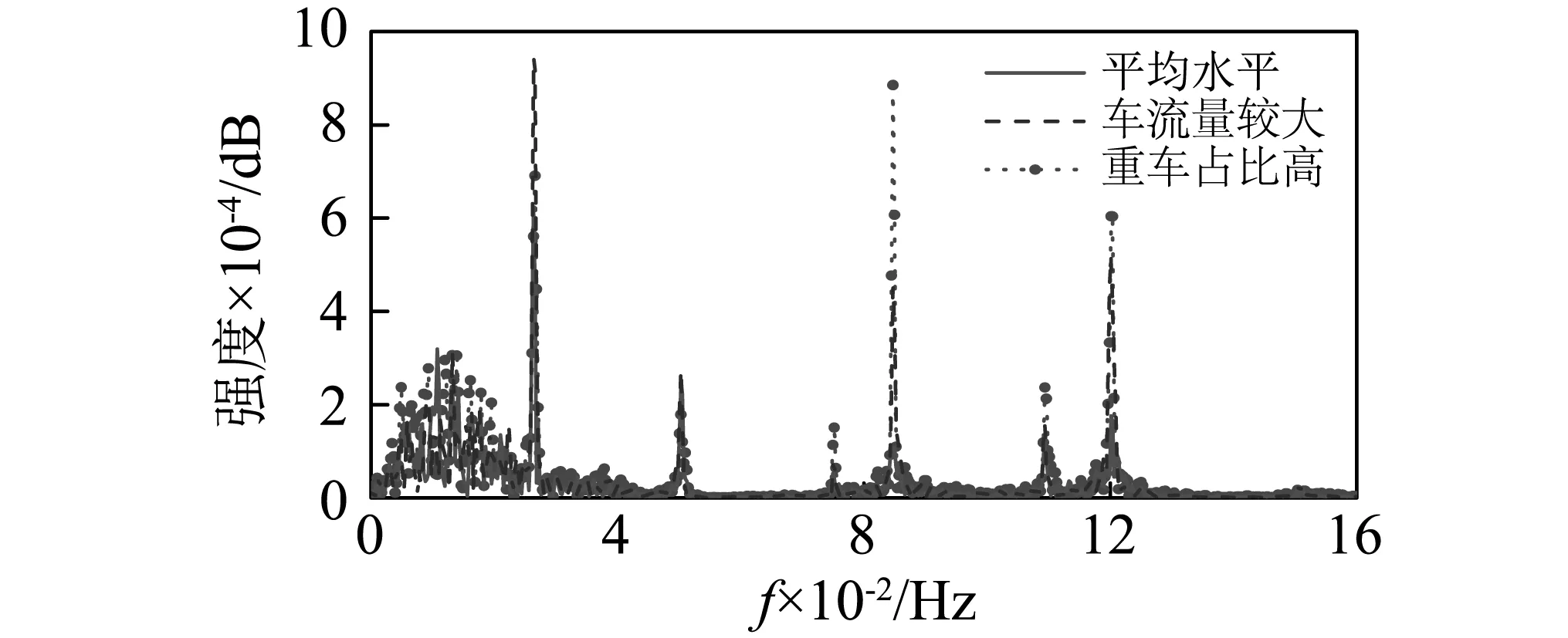
图8 三种交通状况下伸缩缝的纵向位移频谱Fig.8 Displacement spectrum of expansion joint under three traffic conditions

3.3 两种限速措施对伸缩缝位移的影响

大跨钢桥伸缩缝纵向位移响应与车辆荷载特性之间存在着较高的相关性[19]，其中车流速度的提高会导致伸缩缝纵向高频位移量的增加，从而造成累计位移的增长。此外，经过桥梁的小型车虽数量多但自重较轻，故其对梁端位移响应产生的影响较为有限；而大型车辆，特别是载重货车，虽然数量较少，但其经过桥梁时会引起梁端承受更多幅度较大的高频位移。因此，车速较大的重型车辆是引发伸缩缝病害关键因素。基于以上分析，本文提出两种限速措施：①分车型限速措施，小型车按照高速公路设计时速限速(100 km/h[20])，大型载重货车按照设计时速的70%～80%限速；②分时段限速,8 ∶ 00—20 ∶ 00按高速公路设计时速限速，20 ∶ 00—次日8 ∶ 00按设计时速的70%～80%限速。由于夜间重型车所占比例较高，故分时段限速措施从本质上也是限制对载重车辆的车速。

以2011年8月16日的车流量数据为例，根据所提的两种限速措施进行车辆抽样生成随机车流，分析伸缩缝位移响应。与桥梁原100 km/h限速措施的结果(日累计位移量为122.29 m)相比发现，限速措施①可以将累计位移降低16.88%，限速措施②可以将累计位移降低7.98%。因此，两种方法对伸缩缝纵向位移的控制具有一定的效果，可用于缓解伸缩缝病害。

3.4 塔梁阻尼器对伸缩缝位移的影响

为研究塔梁阻尼器对伸缩缝位移的控制作用，在主梁两端增设两只黏滞阻尼器，以COMBIN37单元进行模拟。其中黏滞阻尼器的常数指数α=0.5，阻尼系数c=6 000 kN·(m·s)-α。由“3.1”节的随机车辆模型抽样生成样本集，考虑塔梁阻尼器进行随机车流下伸缩缝位移响应分析并与未考虑塔梁阻尼器的伸缩缝纵向位移响进行对比。图9所示为车速范围为70～80 km/h时有无塔梁阻尼器下伸缩缝位移时程由图可知，阻尼器限制了较为高频的位移，在一定程度上降低了高频位移的幅值。

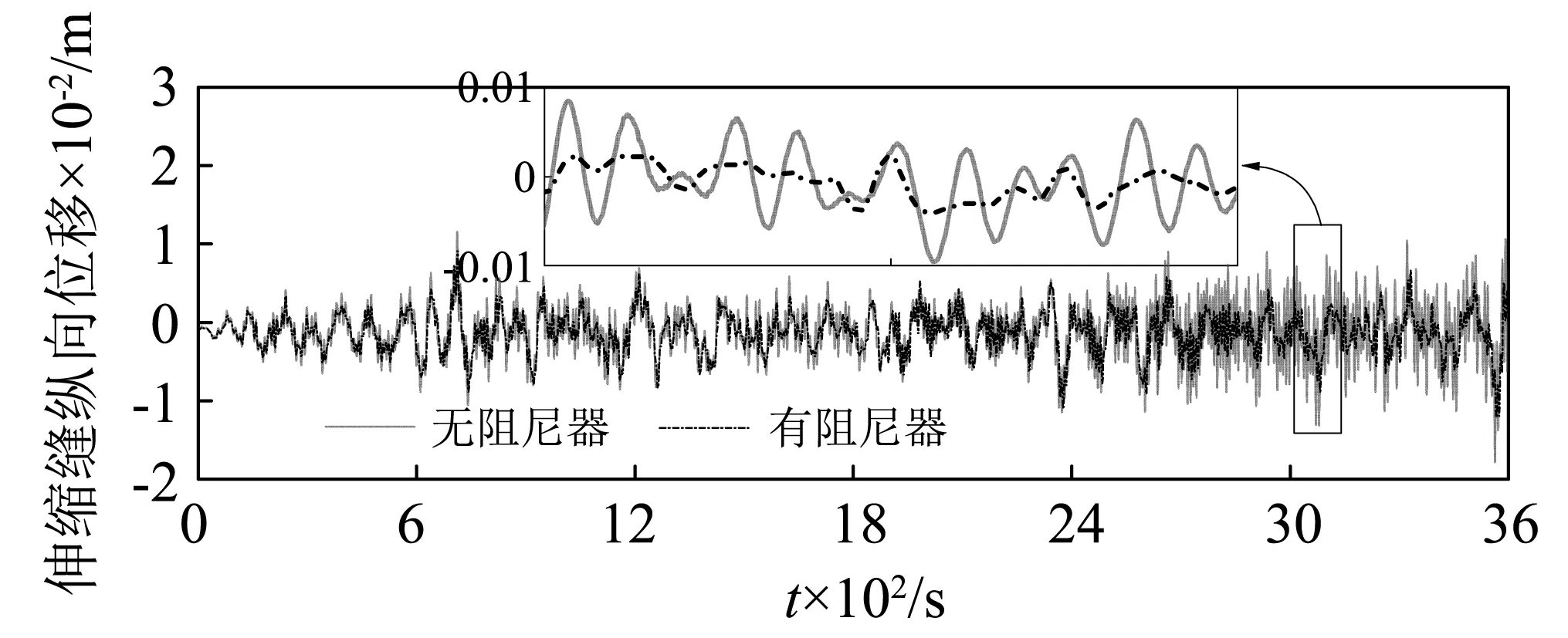
图9 有无桥塔阻尼器下伸缩缝纵向位移相应Fig.9 Displacement response of expansion joint with or without tower damper

图10进一步给出了有无塔梁阻尼器下伸缩缝纵向位移时程(见图9)的频谱图。结果显示：在0～0.05 Hz的频段上，阻尼器的影响并不是很明显，但增设桥塔阻尼器会使较高频段上的强度大幅降低。例如，在0.08 Hz左右的频段上，峰值位移从8.2 dB下降到2.12 dB；在0.12 Hz左右的频段上，峰值位移从11 dB下降到2.82 dB，阻尼器的作用使其分别减少了74.14%和74.36%。此外增设塔梁阻尼器后，伸缩缝的累计位移从4.28 m/h降至2.03 m/h，下降了52.6%左右。故高频位移及幅值的减小可以大幅降低梁端的累计位移，实现病害控制，从而延长伸缩缝的使用寿命。

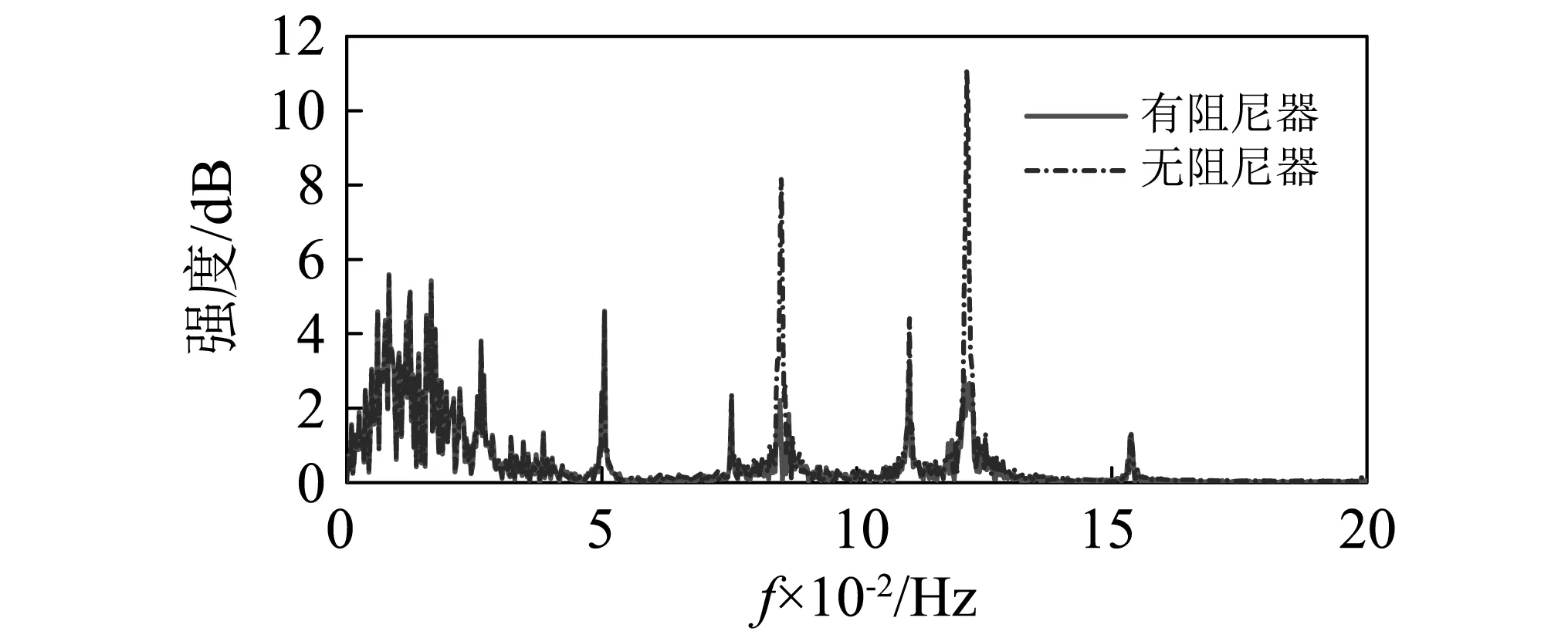
图10 有无桥塔阻尼器下的伸缩缝纵向位移频谱Fig.10 Displacement spectrum of expansion joint with or without tower damper

为了确定阻尼器参数的影响，进行了阻尼系数c和常数指数α对伸缩缝纵向累计位移的敏感性分析，如图11所示。当常数指数α分别为0.3，0.5，0.7和0.9时，阻尼系数c由1 000 kN·(m·s)-α增至30 000 kN·(m·s)-α，伸缩缝累计位移分别下降了69%～96%，42%～79%，20%～59%和7%～36%；当阻尼系数c取不同值时，常数指数由0.9降到0.3，伸缩缝累计位移分别减小了7%～69%，11%～77%，14%～82%，18%～86%，24%～90%和36%～96%。由此可见，通过合理选择常数指数和阻尼系数，可以明显降低伸缩缝纵向累计位移。

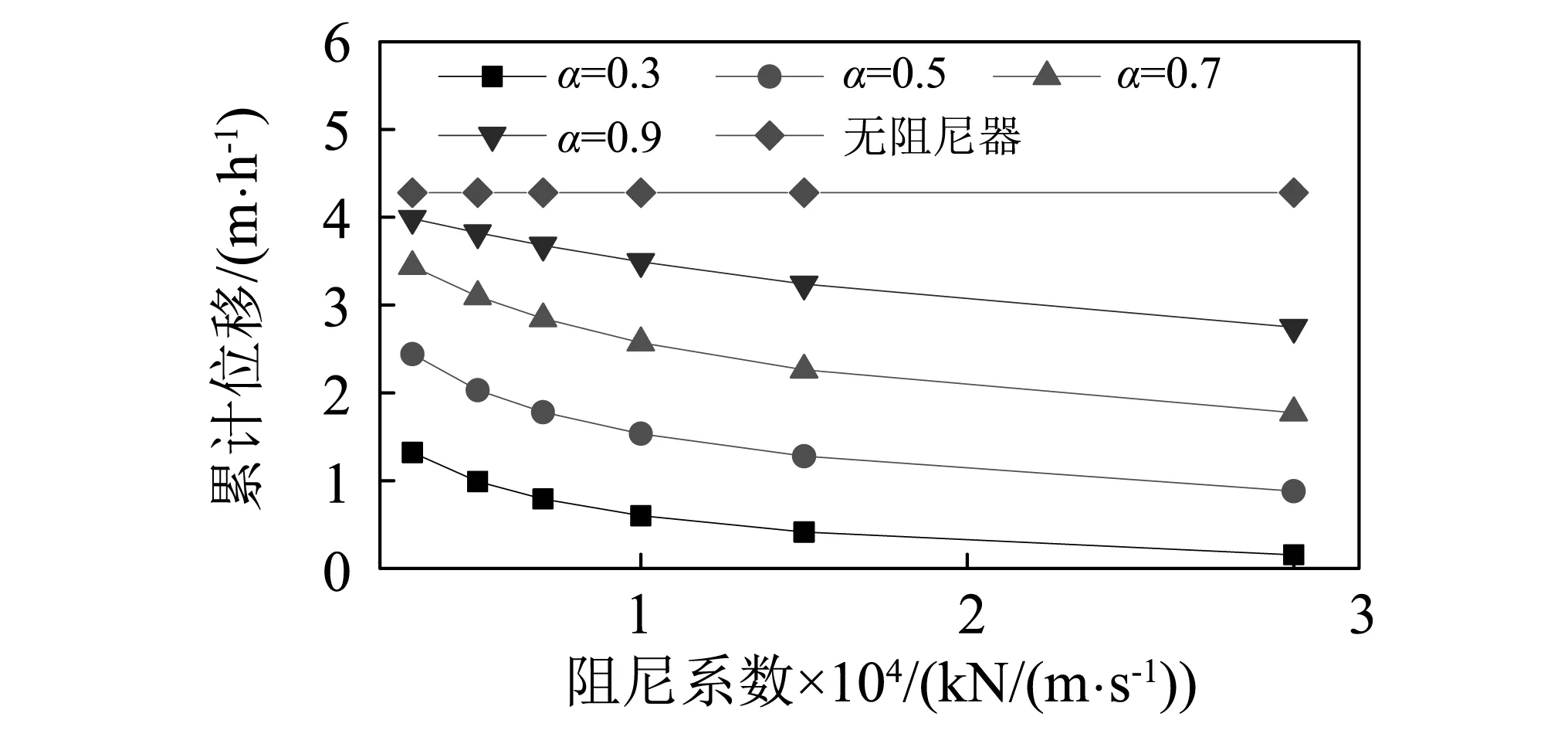
图11 阻尼器参数对累计位移的敏感性分析Fig.11 Sensitivity analysis of damper parameters to longitudinal cumulative displacement

4 结 论

本文结合随机车辆荷载模型和有限元分析，建立了一种随机车流下伸缩缝位移响应的分析方法。研究了车速、车致振动频率、车流量和重型车对伸缩缝纵向位移的影响，并定量分析了分车型限速和分时段限速以及增设桥塔阻尼器对控制伸缩缝病害的效果。根据本文的研究，可以得出以下结论：

(1)由车辆荷载引起的桥梁纵向位移是伸缩缝累计位移的重要成因之一，其中车速和车致振动的频率对累计位移的影响很大。较大的车速和较高的振动频率能够引起伸缩缝产生更多振幅较大的高频振动，从而导致累计位移迅速增加。车流由中速提高到高速时，累计位移会急剧增加，显著地降低伸缩缝的使用寿命，故宜控制上桥车辆的车速。

(2)车流量较大和重型车比例高这两种较为极端的交通状况会显著地增加伸缩缝的累计位移，而重型车的影响更为显著。车辆数的增加会导致高频位移量的增加，而重型车的作用容易在后两个高频段内引起桥梁的共振。因此，在桥梁后期保养中需要重点关注这两种交通状况，优先控制重型车辆的比例，其次在车流高峰期可适当采取限流措施。

(3)所提出分车型限速和分时段限速方案均能显著降低伸缩缝纵向位移累计位移，可用于缓解伸缩缝病害，其中分车型限速方案效果更为明显。此外，增设桥塔阻尼器可显著降低伸缩缝位移幅值、累计位移和高频位移，减小常数指数和增大阻尼系数均能明显降低累计位移。因此，可以通过限制重型车限速和增设桥塔阻尼器的措施控制梁端纵向位移，以减轻缩缝病害。