基于广义有限差分法的输流直管振动响应特性研究

张 挺， 林震寰， 郭晓梅， 张 恒， 范佳铭

(1. 福州大学 土木工程学院， 福州 350116； 2. 台湾海洋大学 河海工程系，台湾 基隆 20224)

管道在输流过程中，因内部流体流动会在管道边壁上施加力的作用，造成振动，并最终导致管道的长期疲劳失效，如输流直管的轴向耦合振动[1]。而对于管道偏离中心轴线造成的横向振动，不同支撑条件对其振动特性也有较大的影响。因此，对不同支撑条件下输流管道动态响应的研究显得尤为重要。

目前，输流管道研究模型主要有梁模型和壳模型两种，在管道内径远小于管道长度时，采用梁模型来研究是简单而有效的。不同学者针对该模型下的输流管道都有着广泛研究，Paidoussis[2]基于梁模型，采用牛顿法对管道单元和流体单元进行受力分析，得到较为完整的描述输流直管横向振动微分方程，并研究了不同支撑条件下输流直管的稳定性问题；随后，又有众多学者对该方程进行不断改进和不同角度的研究。

由于输流直管横向振动微分方程中具有对空间和时间物理量的高阶偏导项，因此其精确解的获取较为困难，目前对输流管道振动响应特性研究采用的数值分析方法主要有伽辽金法(Galerkin Method)[3-5]、微分变换法(Differential Transformation Method，DTM)[6-7]、微分求积法(Differential Quadrature Method，DQM)[8-9]、精细积分法(Precise Integration Method，PIM)[10-11]、广义积分变换法(Generalized Integral Transform Technique，GITT)[12-13]等，这些都可以有效地模拟此类问题。

随着计算机技术和数值方法的不断发展，无网格法(Meshless Method)在近几年有了快速的发展，其中广义有限差分法(Generalized Finite Differential Method，GFDM)属于区域型的无网格法，采用泰勒级数展开搭配移动最小二乘法，将每个点位上的微分量以邻近点的物理量线性累加表示。Benito等[14]提出GFDM法的离散公式，针对其中的一些参数与特性进行一系列的研究，之后将这一方法改良后与其它无网格方法作比较[15]，并使用该方法求解不同类型的偏微分方程，如对流扩散方程[16]、抛物线型方程[17]。同时，Fan等[18]利用此方法求解Burgers方程式，Li等[19]用于求解浅水波方程，均得到了良好的结果。Zhang等[20]采用此方法运用到工程实际问题中，例如数值波浪水槽中非线性波浪的传播、非线性自由液面的液体晃动问题[21]、缓坡方程的求解[22]；Gu等[23]将GFDM方法成功应用于三维热传导的逆时变源问题的精确求解。从这些数值案例模拟的比对结果可以看出，GFDM法在求解高阶偏微分方程问题上具有很大的潜力。

本文针对空间含有四阶偏导项和时间含有二阶偏导项的两端支撑输流直管横向运动微分方程，采用GFDM法和Houblot方法分别对微分方程的空间项和时间项进行离散，建立一种新的高阶精度数值模式，通过与前人的数值结果对比，验证本研究所提出的数值模型的准确性和可行性，在此基础上，分析不同支撑条件对输流直管模型横向振动响应特性的影响。

1 控制方程及边界条件

如图1所示，考虑两端支撑输流直管，管道长度为L，管道轴线为x轴，管道横向为y轴。忽略重力、内部阻尼和流体压力的影响，则其横向运动微分方程可表述为

(1)

式中：Y为管道的横向位移；E为管道的弹性模量；I为管道的横截面惯性矩；mf和mp分别为单位长度管内流体的质量和管道的质量；U为流体流速。

引入无量纲变量

代入式(1)，整理可得两端支撑输流直管的无量纲横向运动微分方程

(2)

针对不同的管道支撑条件，其无量纲化的边界条件可表述为:

(a)两端固支(见图1(a))

(3)

(b)一端固支一端简支(如图1(b))

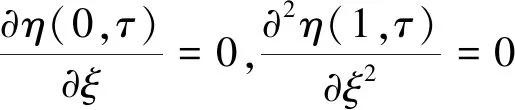
(4)

(c)两端简支(见图1(c))

(5)

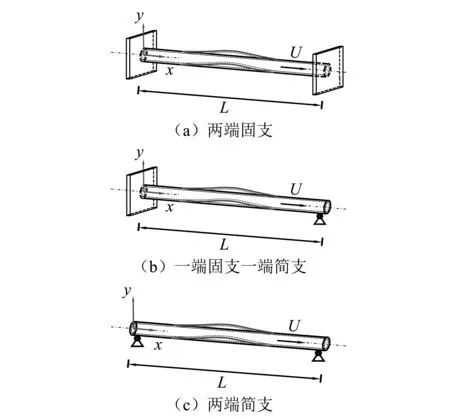
图1 两端支撑输流直管模型Fig.1 Schematic diagram of fluid-conveying pipe

2 数值方法

2.1 广义有限差分法

输流直管横向运动微分方程式(2)，在空间坐标上最高具有四阶偏导项，本文采用广义有限差分法进行离散，其方法是基于移动最小二乘法与泰勒级数四阶展开。首先在整个计算区域内布N个点，再将每个点位上的偏微分项转换成由子区域内各点物理量与权重系数乘积的线性累加。对于区域内的第i点而言，选择ns个最邻近点，形成一个子区域，如图2所示。

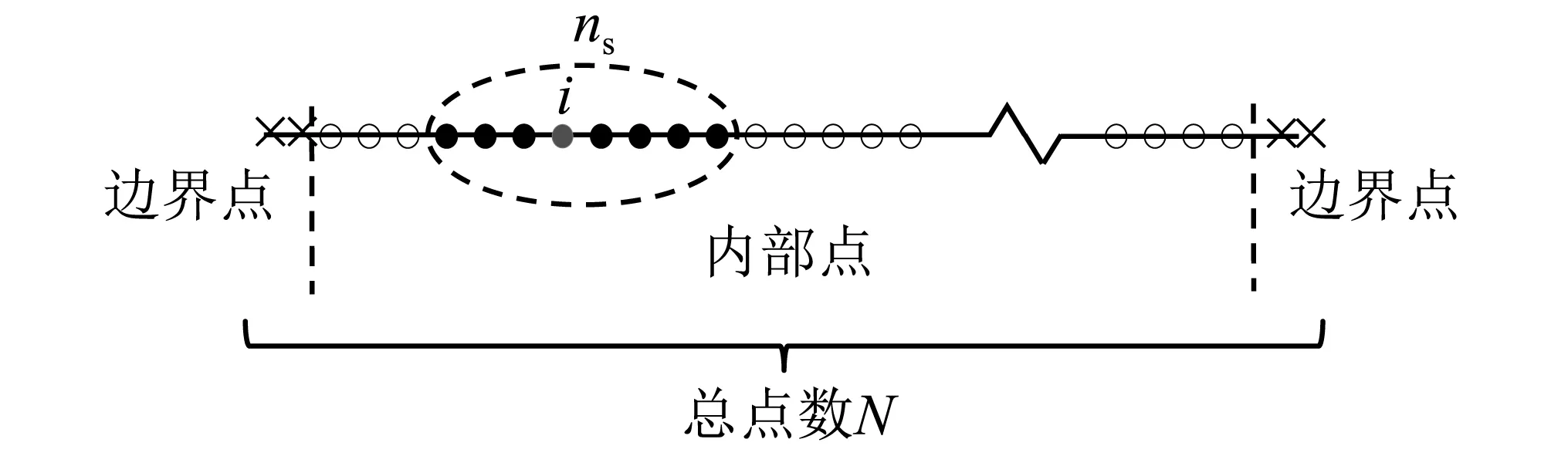
图2 子区域中选择临近点示意图Fig.2 Schematic diagram of nodes in local region

当第i点的子区域形成后，在该子区域内以第i点为中心进行泰勒级数展开，因式(2)对空间项的微分最高阶数为四阶，从而略去四阶以上各项，并定义一个函数B(η)

(6)

式中：j为子区域内的节点编号；δij=ξi-ξi,j为沿着布点方向上第i点与第j点的距离；ξi和ξi,j分别为第i点和第j点的坐标值；ηi,j为第i个子区域中的第j个点的物理量；w(δij)为权重函数

(7)

式中：dmi为第i点与子区域内最远点的距离。

根据移动最小二乘法的思想，将函数B(η)分别对∂η/∂ξ，∂2η/∂ξ2，∂3η/∂ξ3和∂4η/∂ξ4求极小值，可得

A·Dη=b

(8)

其中，

从式(8)可知，系数矩阵A是一个对称矩阵，是由第i点与其子区域内ns个点的物理量计算得到，而矩阵b是由子区域内各节点物理量和空间坐标构成，因此可将矩阵b分解为

b=BQ

(9)

式中：Q=[ηi,ηi,1,ηi,2,ηi,3,…,ηi,ns]T为子区域内第i点和与其相邻ns点的物理量。从而，每一点位上的前四阶偏微分项Dη可表示为

(10)

因输流直管横向运动微分方程式(2)中只含有对空间物理量的一阶、二阶和四阶偏导数，故提取式(10)中每一个点位i上未知物理量(位移)的一阶、二阶和四阶偏微分量的表达式，即

(11)

(12)

(13)

2.2 Houbolt法

由于两端支撑输流直管横向运动微分方程式(2)，在时间坐标上最高具有二阶偏导项，本文采用Houbolt法对时间项进行离散。该法属于四点格式的隐式时间积分法，具有二阶精度且无条件稳定，即通过对n-2，n-1，n和n+1四个时刻的位移η进行三次插值来近似表示其一阶时间导数∂η/∂τ和二阶时间导数∂2η/∂τ2，其表达式为[24]

(14)

(15)

因Houbolt法在求解未知时间层物理量ηn+1时，需已知前两个时间层的物理量ηn-1和ηn-2，从而需要起步条件，本文采用Euler法进行起步，即

(16a)

(16b)

2.3 方程离散

首先，使所有内部点满足控制方程式，采用GFDM对控制方程式中的空间变量偏微分进行离散，即将式(11)～式(13)代入式(2)中，可得

(17)

其次，使所有边界点满足对应的边界条件，采用GFDM法对边界条件进行离散可得：

(1)两端固支

(18)

(2)一端固支一端简支

(19)

(3)两端简支

(20)

式(17)结合边界条件式(18)～式(20)中的一种，可定义一种支撑条件下输流直管的动力学方程组，即：

(21)

式中：M，C，K分别为离散系统的质量矩阵、阻尼矩阵和刚度矩阵；η为待求物理量未知矩阵。

对式(21)可进行模态分析，设方程式的特解为

η=φeλτ

(22)

式中：φ为N阶位移幅值列阵。

将式(22)代入式(21)中，可得两端支撑输流管道的广义特征值问题

(λ2M+λC+K)φ=0

(23)

其特征方程可表述为

|λ2M+λC+K|=0

(24)

上式是关于λ的2N次实系数代数方程，设无重根，通过求解可得2N个共轭对形式的互异特征值λ，其值通常为复数，虚部即表示输流管道振动频率。

同时，采用Houbolt法对式(21)中的时间项一阶和二阶微分进行离散，可得每一内部点位i上的两端支撑输流直管横向振动微分方程的离散形式，即

(i=3,4,…,N-2)

(25)

式(25)结合边界条件式(18)～式(20)中的一种，可定义一种支撑条件下输流直管的线性代数方程组为

[C]N×N·{η}N×1={f}N×1

(26)

式中：C为稀疏矩阵；f为控制方程式与边界条件离散后的非齐次项；η为待求未知矩阵。结合不同案例的初始条件，通过式(26)即可求得不同支撑条件下输流直管在不同时刻，每一点位上的物理量。

3 数值模型验证

为了验证本文所提出的数值模式的准确性和鲁棒性，本节对两端支撑轴向运动梁模型和两端固支输流直管模型进行数值模拟，并与前人所做研究结果进行对比，其中当流体流速u用管道横向运动速度代替，式(2)即转化为两端支撑的梁模型。

3.1 两端支撑梁模型

当管道运动速度u=0时，两端支撑梁模型退化为简单的直梁模型，其前N阶固有频率具有精确解，采用总点数N=604，时间步长Δt=0.001，表1给出了GFDM法计算得到的不同支撑条件下直梁模型前四阶固有频率，与DTM、DQM以及Thomson的精确解[25]研究成果进行对比，吻合良好，说明该数值模式具有相当高的精度。为了进一步说明其计算效率，本文也将三种不同数值方法的计算时间列于表1，虽然GFDM的总布点数N达604，但所用计算时间均在0.85 s左右，低于DTM(N=17)，部分高于DQM(N=60)，这是由于应用GFDM法对控制方程进行离散后，所得到的代数方程组的系数矩阵为稀疏矩阵，因此可提高计算效率。

当管道运动速度u=0.5时，给定初始条件为

(27)

以管道两端固支为例，计算得到管道中点处振幅η的时间历程，如图3所示。可见，应用GFDM法得到的结果与An等研究中采用GITT法得到的结果吻合良好。图3中分别采用了不同总点数N(见图3(a))、不同时间步长Δt(见图3(b))和不同选点数ns(见图3(c))进行数值模拟，结果表明，随着总点数N和选点数ns的增加或时间步长Δt的减小，GFDM的计算结果与An等研究中的数值结果越接近，说明本文提出的数值模式具有良好的稳定性。

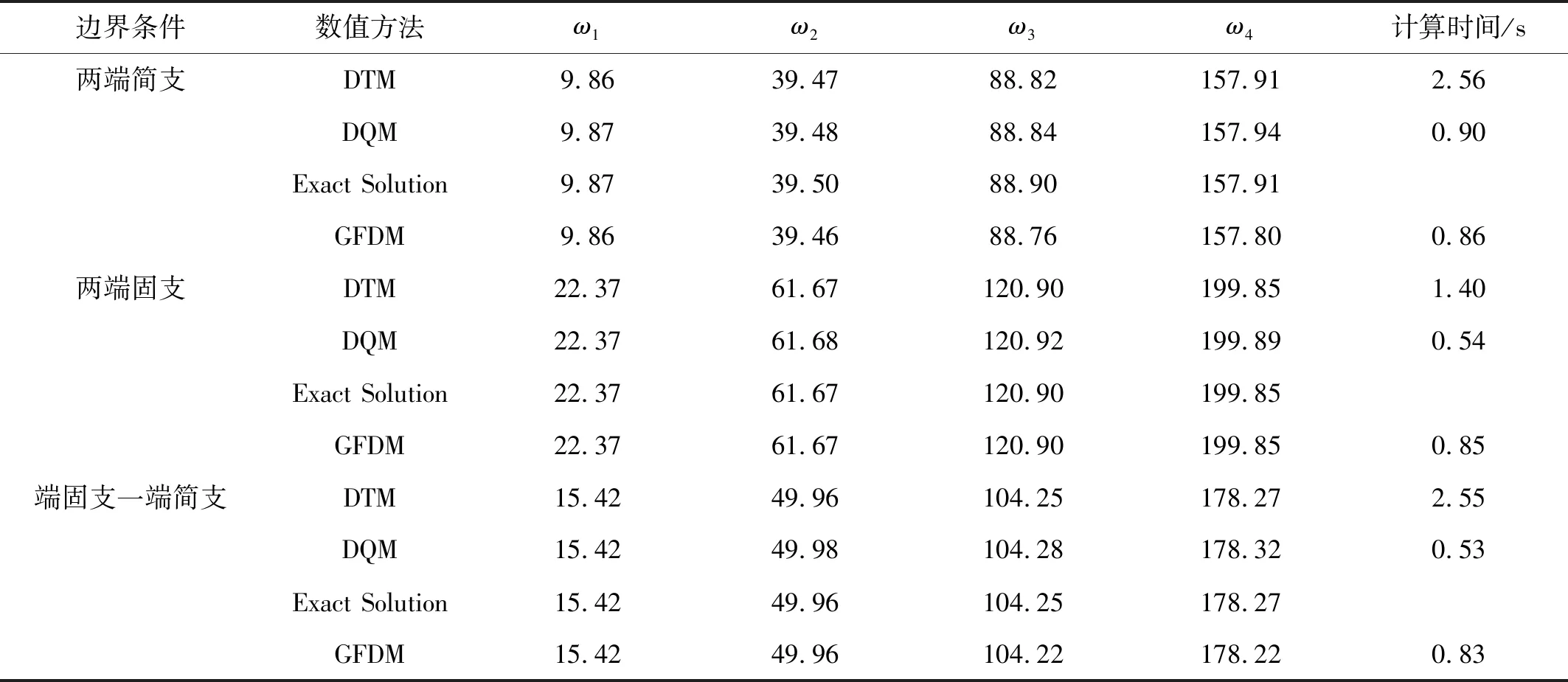
表1 两端支撑梁固有频率(u=0)

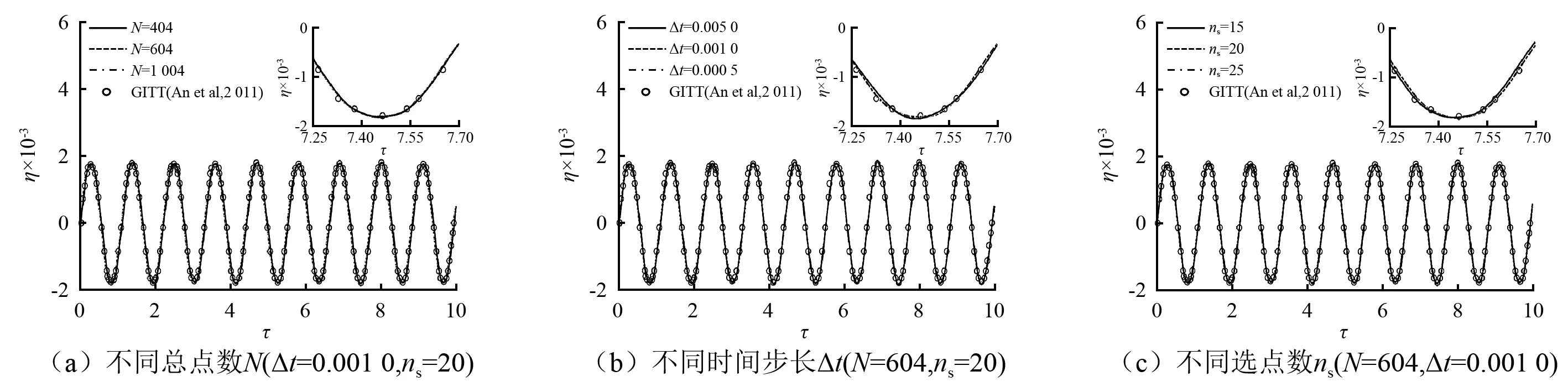
图3 两端固支梁受迫振动中点处振幅比较(u=0.5)Fig.3 Comparison of amplitudes at midpoint of forced vibration of clamped beam at u=0.5

3.2 两端固支输流直管模型

同样以两端固支输流直管模型为例，在流体流速u的作用下，输流直管将出现受迫振动，本节数值模型参数分别取N=604，ns=20，Δt=0.001 0，同时给定初始条件为

(28)

图4为不同流体流速u和不同质量比β输流直管中点处位移的时间历程。将数值结果与Gu等的研究成果进行对比，结果也是非常吻合,进一步说明了本文所提出的数值模型具有较高的精确度。从图4可知，在相同流速u情况下，随着质量比β的增加，两端固支输流直管中点处的振动速率加快，而振幅无明显变化，见图4(a)和图4(b)所示。在相同质量比β情况下，随着流体流速u的减小，两端固支输流直管中点处振动幅值减小，但振动速率加快，见图4(a)和图4(c)所示。

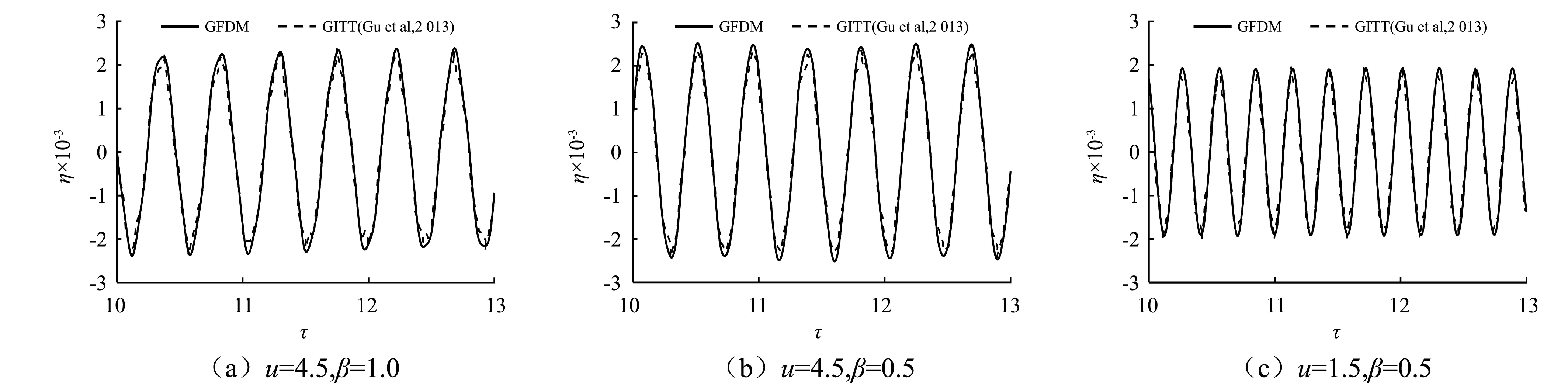
图4 不同流体流速u和质量比β两端固支输流直管中点振幅比较Fig.4 Comparison of amplitudes at midpoint of differential fluid velocity and mass ratio of clamped-clamped pipe conveying fluid

4 不同支撑条件下输流直管振动响应

当管道在输流过程中，由于端部约束限制条件不同，其振动响应特性也将不同。为了进一步研究支撑条件对输流直管横向振动响应特性的影响，本节针对三种不同支撑条件(两端固支、两端简支和一端固支一端简支)下输流直管进行模拟。数值模型参数仍取总点数N=604，时间步长Δt=0.001，子区域选点数ns=20，流体流速u=1.5，质量比β=0.5。

图5(a)给出了三种不同支撑条件的输流直管中点振动幅值时程，从图5(a)可知，输流直管均作周期性有规律的振动，当两端简支时输流直管中点处的振幅最大，一端固支一端简支时次之，而两端固支时输流直管中点处的振幅最小，为两端简支时的一半；为了进一步了解三种不同支撑情况下管道中点处的频域响应，通过傅里叶变换得到了三种不同支撑条件下输流直管中点处的频谱图，如图5(b)所示。不同支撑条件下输流直管均只出现一阶主频，两端简支(f=1.34)时振动频率最小，两端固支(f=3.42)时振动频率最大，而一端固支一端简支(f=2.32)时介于二者之间。

图5 不同支撑输流直管中点处振幅比较Fig.5 Comparison of amplitudes at midpoint of pipe conveying fluid for different boundary conditions

图6为输流直管在τ=13时刻全管振动幅值曲线。可见，在忽略重力、内部阻尼和流体压力影响的条件下，两端简支和两端固支其振动响应最大值出现在输流直管中点处，对于一端固支一端简支支撑条件，因两端支撑条件不对称且简支端约束限制较低，致使管道振幅最大值出现位置向右偏移。

图6 τ=13时不同支撑输流直管振幅比较Fig.6 Comparison of amplitudes of pipe conveying fluid for different boundary conditions at τ=13

5 结 论

本文针对空间上最高具有四阶偏导项和时间上最高具有二阶偏导项的两端支撑输流管道横向运动微分方程，采用区域型无网格法分析了两端支撑轴向运动梁模型和两端固支输流直管模型的横向振动问题，对于该问题在空间和时间上分别采用GFDM法和Houblot法进行离散，建立高阶精度的无网格法数值模式。

(1)通过与前人研究成果进行比较以及方法本身影响因素(总点数N、时间步长△t和子区域选点数ns)测试对比，结果吻合良好，表明所提出的数值模型在求解输流直管振动响应问题上具有良好的准确性和鲁棒性。

(2)对比分析了三种不同支撑(两端固支、两端简支和一端固支一端简支)下输流直管振动响应特性，结果表明，输流直管均以一阶主频作周期性有规律的振动，在对称支撑(两端简支和两端固支)情况下，振幅与振动频率成反比，即振幅越大，频率越小；在非对称支撑(一端固支一端简支)时，振动幅值和频率介于两种对称支撑之间，且振幅最大值出现位置向右偏移。

本文仅针对在忽略重力、内部阻尼和流体压力影响的条件下两端支撑的水平输流直管进行研究，从本文研究测试的结果可以看出，由于GFDM法可将每个点位上高阶微分项进行快速转换为线性代数方程组，因此具有较大的潜力，下一步可将其运用到输流管道非线性振动和弯曲输流管道的研究中。