转子支承系统临界转速概率分析的随机响应面法

左彦飞， 江志农， 冯 坤， 王建军

(1. 北京化工大学 机电工程学院，北京 100029； 2. 北京航空航天大学 能源与动力工程学院，北京 100191)

工程中的转子支承系统存在许多非确定性因素，主要包括：部件在公差范围内的加工误差，材料的不均匀，部件间装配的随机性，长期工作导致的磨损，热致几何变形等[1]。这些不确定因素可致使设计相同的转子系统临界转速产生大幅变化。例如，某型发动机不同台次临界转速相差可达10%[2]，即使同一台发动机，重新拆装一次，其临界转速和振动特性也可能发生很大变化，这给发动机结构可靠性设计及振动控制带来一系列问题。研究转子系统临界转速在不确定因素影响下的概率分布规律，在设计上可尽量避免转子系统工作在临界转速附近，提高系统可靠性；在振动控制上可通过控制加工或装配过程中的敏感参数，减小振动故障发生的可能性，因而具有重要意义。

目前较为成熟的概率分析方法主要面向叶片、轮盘等核心部件优化设计[3-4]，而与转子动力学结合的转子系统级别的不确定性分析方法近几年刚受到关注，主要使用的方法有蒙特卡洛法、区间分析法和随机多项式展开法(Polynomial Chaos Expansion)。其中，蒙特卡洛法直接对不确定因素进行抽样计算，计算量巨大，特别是使用三维实体有限元转子模型时，消耗的计算资源和时间往往无法承受。区间分析法是在统计信息不足以描述非确定参数的概率分布或隶属函数时使用的方法，用以获得响应的区间范围[5-6]。随机多项式展开在转子不确定性稳态响应分析中应用较多[7-10]，不过，该方法直接对动力学方程进行随机多项式展开，主要适用于可以直接由动力学方程求解的问题。而对于不能直接由系统方程求解的问题，特别是由Campbell图求系统临界转速时，随机多项式展开法适用性较差。

为此，本文直接从临界转速与转子系统力学不确定参数的隐式函数关系入手，将可靠性分析使用的随机响应面法引入转子支承系统的临界转速概率分析中，提出基于随机响应面的转子支承系统临界转速概率分析方法。

1 非确定因素在转子动力学方程中的表达

转子系统中非确定因素主要包括转子材料属性的不确定性、部件几何加工的不确定性、连接结构刚度的不确定性等。由于三维实体有限元转子模型能准确模拟系统的主要结构和力学特征，易于考虑离心力和陀螺效应的影响，应用越来越广泛[11-14]，因此，本文采用三维实体有限元格式建立具有非确定因素的转子动力学方程。

1.1 部件材料属性的不确定性

材料属性的不确定性来源于部件材料本身的不均匀甚至缺陷或在加工处理过程中产生的特性变化。设系统中存在l种独立材料属性，随机变量ξi是某种符合材料密度分布规律的随机变量，如标准正态分布，则第i个部件材料的密度可以表示为

ρi=ρ0i+ξiρσi, (i=1,2,…,l)

(1)

式中：ρ0i为密度的均值；ρσi为密度的标准差。类似的设ξl+i为符合材料弹性模量分布规律的随机变量，则材料的弹性模量可以表示为

Ei=E0i+ξl+iEσi, (i=1,2,…,l)

(2)

式中：ξ0i为弹性模量的均值；Eσi为弹性模量的标准差。将式(1)代入参考文献[15]中基于三维实体有限元的转子系统动能表达式，将式(2)代入势能表达式，进而得到质量矩阵，陀螺矩阵及刚度矩阵非确定形式

(3)

1.2 部件几何加工的不确定性

在部件的加工过程中，不可避免存在尺寸公差和形位公差，这些公差使得实际部件与理想部件在几何形状上存在差异。如图1所示。

图1 理想结构的几何形状与实际结构的几何形状Fig.1 Ideal structure geometry and actual structure geometry

而在工程实际中，图1(b)所示几何加工误差通常是在公差范围内的误差，对几何形状的影响非常小。因此，本文仅将几何加工误差的不确定性简化为不平衡量的不确定性。

将上述转子结构的几何加工不确定性和“1.1”节中密度不确定性统一简化为转子上某些特定位置(动平衡修正面或转子各个盘上)的外加不平衡量。假设有m个不平衡量(不平衡质量与偏心量的积)施加位置，则设ξ2l+1～ξ2l+m是符合不平衡量大小分布特性的随机变量，ξ2l+m+1～ξ2l+2m是符合各个不平衡量相位分布的随机变量，则各个位置上的不平衡量激励可以表示为

Ω2fi(ξ2l+i)exp(jΩt+α(ξ2l+m+i)),
(i=1,2,…,m)

(4)

式中：fi(ξ2l+i)为i位置的随机不平衡量的大小；α(ξ2l+m+i)为该不平衡量相对于零相位的相位角。

1.3 连接部位刚度不确定性

转子支承系统中的连接关系主要包括螺栓连接、轴承等。这些连接结构刚度的不确定性主要来源于安装状态的随机性，转子系统运转过程连接界面的变化，轴承游隙的不确定性等[16]。假设转子系统有n处主要的不确定性连接关系，设随机变量ξ2l+2m+1～ξ2l+2m+n是符合连接刚度大小分布规律的随机变量，则第i处连接刚度的不确定性表示为

Ki(ξ2l+2m+i)=K0i+ξ2l+2m+iKσi, (i=1,2,…,n)

(5)

式中：K0i为连接结构刚度矩阵的平均值；Kσi为连接结构刚度矩阵的标准差。

此外，连接界面的变化一般也会对转子系统的不平衡量造成影响，本文将这种影响一并纳入式(4)中予以考虑。

1.4 考虑不确定性的转子动力学方程的一般形式

将上述所有随机变量用向量的形式表示，即令

ξ={ξ1ξ2…ξN}T, (N=2l+2m+n)

(6)

则考虑不确定因素的转子动力学方程的一般形式为

(7)

在双转子系统中，忽略式(7)中的阻尼项，得到对应的无阻尼双转子支承系统的动力学方程的一般形式为

(8)

式中：M(ξ)为系统质量矩阵；f(ξ)为系统激励向量；Ω1，Ω2分别为转子1、转子2的转速；G1，G2分别为转子1、转子2旋转产生的陀螺效应矩阵；K1(ξ)，K2分别为与转子1、转子2转速相关的刚度矩阵，可简称为旋转刚度矩阵；K0(ξ)为与转速无关的系统刚度矩阵。此外，还存在其他不确定性因素，例如热致几何变形等，所有这些因素，在转子系统动力学方程中最终表现为两大类。

第一类是造成转子系统本身变化的不确定性因素。例如，材料的不确定性对转子动力学方程中的质量矩阵，陀螺矩阵，刚度矩阵都有影响。这些因素导致转子系统的固有特性(包括临界转速)存在不确定性。

第二类是造成转子系统所受激励变化的不确定性因素。例如，几何加工的不确定性(简化处理)，密度的不均匀，装配的随机性等，都对转子不平衡量的大小、相位产生不确定性影响，但简化处理后并不影响转子系统的固有特性。

2 基于随机响应面的临界转速分析方法

2.1 具有不确定性的双转子系统临界转速

以无阻尼双转子系统临界转速不确定分析为例，阐述临界转速概率分析方法。式(8)的齐次形式为

(9)

该方程需要变换到状态向量空间进行求解。设转子系统的自由度为n， 引入2n维状态向量

(10)

将式(9)改写为状态方程

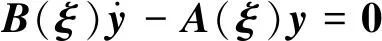
(11)

其中，

设其解的形式为

y=ψeλt

(12)

将式(12)代入式(11)得

A(ξ)ψ=λB(ξ)ψ

(13)

求解式(13)可得n对共轭复特征值和n对共轭复特征向量

(14)

式中：σi为特征值的实部，表征衰减系数；ωi为特征值虚部，表征系统的固有频率； j为虚数单位；φ为原方程即式(13)的模态振型。在具有不确定性的双转子支承系统中，由于旋转的影响，λi，ψi的实部和虚部都是转子转速Ω1，Ω2及随机变量ξ的函数。

若已知Ω1与Ω2的函数关系

Ω2=f(Ω1)

(15)

可将式(14)双转子系统的固有频率表示为函数向量的形式

ω(Ω1,f(Ω1),ξ)={ω1ω2…ωn}T
(ω1≤ω2≤…≤ωn)

(16)

实际中，基于数值计算并不能得到ω中各固有频率函数的解析表达。在确定性分析中，一般根据需要，选择在关心的转速范围内求解若干组(Ω1,f(Ω1))(或(f-1(Ω2),Ω2))对应的ω中各固有频率的函数值，将不同转速下的特定振型所对应的固有频率值平滑连线，近似得到各固有频率的函数曲线。Campbell图方法就是以Ω1(或Ω2) 为横坐标，以固有频率(正频率)值为纵坐标，将各个固有频率函数随Ω1的变化曲线画出，做激励线

ω=Ω1或ω=Ω2

(17)

交点即为临界转速。然而，由于式(16)中固有频率函数同时受不确定因素ξ影响，通过直接求交点的方式获取临界转速概率分布规律的计算量和分析难度都很大。

2.2 转子系统临界转速的随机响应面

为了提高临界转速概率特性分析效率，本文引入了可靠性分析中的随机响应面分析方法。由临界转速求解过程及式(16)、式(17)可知，临界转速与随机变量ξ存在隐式函数关系。数学上可以证明[17]，某一阶临界转速可以表示为

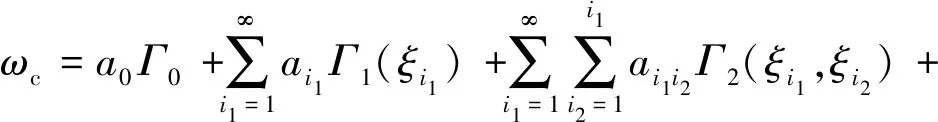
(18)

式中：ai1…ir为随机多项式系数；Γp(·)为括号内变量的p阶随机多项式。式(18)中，当p趋于∞时，等式两边相等。为了便于表达，对于N维随机变量，可以改写为

(19)

(20)

式中：M为保留的项数，可由

(21)

2.3 随机响应面系数的拟合

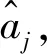
对于随机响应面法，通常采用线性无关概率配点法选取输入样本，该方法所需的配点数目只需要等于待定系数数目即可得到满意的结果[18]。此外，中心复合抽样(Central Composite Design，CCD)，Box-Behnken Matrix Sampling(BBM)，也可用于随机响应面法的系数拟合，不过其基本要求是样本数量大于未知系数数目。关于随机响应面法的系数拟合及抽样方法，相关研究已经比较充分，可以通过通用有限元程序或MATLAB方便实现。

3 典型双转子支承系统临界转速概率分析实例

本节以典型双转子支承系统临界转速概率分析为例，验证随机响应面法在实际应用中的精确性和高效性。

3.1 转子系统临界转速的随机响应面

某典型双转子支承系统的模型如图2所示。在该转子支承系统中，轴承位置的刚度，套齿连轴器等的连接刚度都存在非确定性。根据工程分析需要，假设1号轴承位置的水平支承刚度K1y(ξ1)， 2号轴承位置竖直支承刚度K2z(ξ2)， 刚性套齿连轴器的弯曲刚度K65(ξ3)存在非确定性， 且ξ1,ξ2,ξ3均符合标准正态分布，K1y(ξ1)，K2z(ξ2)的标准差为均值的5%，K65(ξ3)的标准差为均值的10%。

图2 典型双转子支承系统Fig.2 Typical dual rotor support system

3.2 临界转速概率分析随机响应面法准确性验证

利用随机响应面法依据式(20)低压转子激励(ω=Ω1)的某阶临界转速可以表示为

(22)

本文采用中心复合抽样法拟合上述未知系数，在示例中，不确定参数个数为3，随机多项式阶次为2，共10个未知系数，依据参考文献[19]以及ANSYS中概率分析样本选取方法，共需要15个样本点，因此，只需对双转子支承系统进行15次确定性分析，利用“2.1”节中介绍的Campbell图法得到15个样本点对应的该阶临界转速值，然后进行非线性拟合，得到ac0～ac9的值，最后利用式(22)进行蒙特卡洛抽样，对该阶临界转述进行概率特性分析。为了验证随机响应面法计算结果的准确性，同时使用基于蒙特卡洛法对低压转子激励的第1阶正进动和第2阶正进动临界转速的不确定性进行分析。图3所示为低压转子激励第1阶正进动临界转速(1stF)频数分布直方图，其中图3(a)为由蒙特卡洛方法(Monte Carlo Simulation，MCS)1000次抽样得到的计算结果，图3(b)为5 000次随机响应面(Stochastic Response Surface Method，SRSM)抽样计算结果。由于蒙特卡洛法耗费计算时间太长，在抽样1 000次后所得临界转速平均值和方差均已收敛，所以此处并未进行5 000次抽样计算。图中红色曲线为拟合得到的标准正态分布曲线，两种方法计算得到的第1阶临界转速的分布规律都符合正态分布。图4所示为低压转子激励第2阶正进动临界转速(2ndF)频数分布直方图，第2阶正进动临界转速也符合正态分布。不过，第2阶正进动临界转速的变化范围较大，也就是标准差较大。表1所示为蒙特卡洛法与随机响应面法计算得到的临界转速的均值和标准差的比较。

图3 第1阶正进动临界转速(1st F)频次分布直方图Fig.3 1st order positive precession critical speed (1st F) frequency distribution histogram

图4 第2阶正进动临界转速(2nd F)频次分布直方图Fig.4 2nd order positive precession critical speed (2nd F) frequency distribution histogram

从表1可知，利用随机响应面法得到的临界转速均值与方差与蒙特卡洛法得到的计算结果一致。在所假设的随机变量的影响下，第1阶正进动临界转速变化较小，标准差约为1 r/min，根据正态分布的概率分布密度函数可知，低压转子激励第1阶正进动临界转速在(2 269±3) r/min的概率约为99.73%，变化范围非常小。而对于第2阶正进动临界转速，其标准差约为50 r/min，转子第2阶临界转速在(5 513±150) r/min的概率约为99.73%。

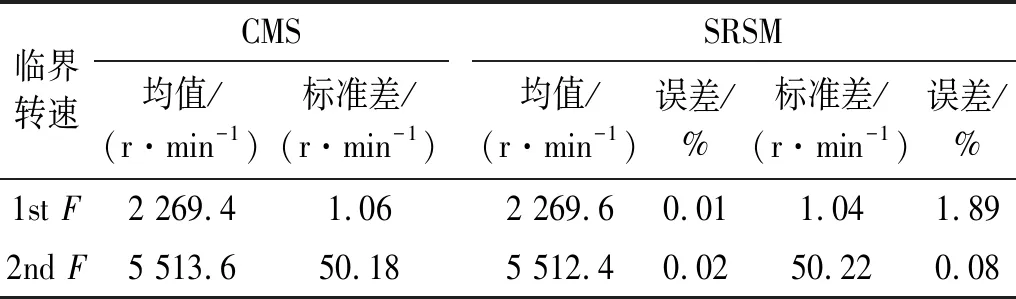
表1 蒙特卡洛法与随机响应面法计算临界转速结果比较

3.3 临界转速概率分析随机响应面法的高效性

上述概率振动特性分析实例，已经充分验证了随机响应面法应用于转子系统临界转速分析的准确性，下面比较随机响应面法与蒙特卡洛法的计算效率。表2所示为使用有限元模型，依据参考文献[20]获得的减缩模型及随机响应面法进行1 000次蒙特卡洛抽样计算所占用的计算机内存及消耗的计算时间。直接用原模型进行1 000次蒙特卡洛抽样计算临界转速，稳态不平衡响应，所消耗的时间预计为136.9万 s(15.8 d)，使用减缩模型后，时间缩短到1.78万 s(4.9 h)，而利用减缩模型加随机响应面法分别只需要267 s(4.5 min)。而上述计算使用的是同一台计算机，可见，随机响应面法可以大幅提高分析效率。

表2 随机响应面法与蒙特卡洛法计算效率比较

4 结 论

针对工程中具有不确定性转子系统临界转速概率分析的需要，本文提出了一种基于随机响应面的转子系统临界转速概率分析方法。并应用该方法对典型双转子支承系统临界转速的概率分布规律进行了分析，验证了方法的准确性和高效性。相关结论主要有以下几点：

(1) 转子系统部件材料的不确定性影响转子系统的质量矩阵、陀螺矩阵和刚度矩阵，几何加工的不确定性经过简化后，可以近似为对转子系统不平衡量的影响，连接关系的不确定性主要表现为对系统刚度矩阵的影响，同时材料不均匀及连接关系的变化也会对不平衡量的大小和分布产生影响。最终，依据作用效果，可将所有不确定因素分为系统不确定性和激励不确定性两类。

(2) 基于随机响应面法的转子临界转速概率特性分析利用随机响应面直接拟合转子系统中不确定性输入参数与临界转速的隐式函数关系，利用所得到的函数关系表达式替代系统的有限元模型进行蒙特卡洛分析。对典型双转子支承系统临界转速的概率分布计算结果表明，该方法与利用蒙特卡洛方法分析得到结果一致。

(3) 该方法只需要利用有限元模型进行少量样本计算，相比于利用有限元模型进行的蒙特卡洛分析，随机响应面法的分析效率得到大幅提升。

不过，随机响应面法收敛性得以保证的前提是所有随机变量都必须符合某种特定的分布，才可能找到与这种分布对应的正交多项式作为随机多项式的基。例如与高斯分布对应的是Hermite多项式，与Gamma分布对应的是Laguerre多项式。而在实际转子支承系统中的随机变量不一定都符合同一种分布规律，因此该方法在复杂转子支承系统中的应用可能会受限制。另外，本文分析过程中假设不确定因素不会对转子的轴对称性造成影响，该假设对于大多数轴对称转子系统适用，但对于非对称转子系统如裂纹转子、异形转子等并不适用，由于这类转子系统一般都具有时变特性，需要使用时变系统动力特性分析方法进行分析，不存在确切的“临界转速”定义，故本文未予研究。