高速运动的轨道图像去模糊

2019-12-31鄢化彪黄绿娥

铁道学报 2019年12期

鄢化彪，黄绿娥，王鹏

(1.江西理工大学理学院,江西赣州 341000；2.江西理工大学应用科学学院,江西赣州 341000；3.中国铁道科学研究院机车车辆研究所,北京 100044)

中国铁路的发展处于跨域式进步阶段,高速铁路、地铁和轻轨等各种轨道交通正在大规模建设。根据《铁路“十三五”发展规划》[1],到2020年,全国铁路营业里程将达到15万km,其中高速铁路3万km。如何确保这么长的轨道运行于安全状态,目前大多是基于费工耗时的人工检测,基于机器视觉的轨道缺陷检测系统将取代人工检测成为趋势[2-3]。采用机器视觉来检测轨道状态及其周边运行环境,或将图像检测设备直接安装在运行机车上,监测轨道及周围环境的安全运行状态。

但由于各种复杂因素的影响,如运动、失焦、噪声等，将导致采集的轨道图像质量退化,甚至严重模糊而使图像无法进行下一步的图像识别。因此，如何提高图像质量对进一步的模式识别很重要。由于车载相机中焦距固定,本文主要考虑高速运动相机导致的模糊,即在曝光时间内的相机运动导致采集的图像产生的模糊。

几乎所有的去模糊方法都认为模糊图像是由原始清晰图像与未知模糊核卷积而成[4-6]。去模糊则是反卷积的过程,这个反问题是病态的。一般用正则化的方法最小化估计图像和清晰图像的差,从而缩小解空间范围使其良态化,但会出现一些过度平滑[7]。文献[8]认为自然图像梯度服从长尾分布,模糊核亮度直方图是稀疏的,采用变分的方法来估计核函数,然后反卷积去模糊。文献[9]认为自然图像梯度服从拉普拉斯分布,并建立最大后验概率MAP模型来估计核函数,最后用期望最大化EM算法进行优化。文献[10]结合图像噪声、图像梯度和核函数这些先验知识来减少振铃效应。文献[11]认为相机的抖动是非统一化的模糊,并建立广义运动模糊的概念。文献[12]考虑相机的前向及后向运动,但在估计模糊核时需要手动选择。文献[13]提出快速去运动模糊算法,通过引入一个新的预测步骤以及在图像梯度方面的操作,减少图像去模糊步骤和提高模糊核估计的速度。在预测步骤,该算法从复原出的清晰图像中提取强边缘,然后仅用这些边缘估计模糊核。

如上所述,图像运动去模糊的研究针对不同的应用场合及适用范围在处理时间和效果上有很多不同的方法,目前这些引用量较高的算法大多数没有考虑图像反卷积后的复原质量,也就是没有进一步客观评价图像复原后的质量,有些算法也只是通过有参考图像的评价指标,如峰值信噪比(Peak Signal to Noise Ratio，PSNR), 均方误差(Mean Square Error，MSE)和结构相似度(Structural Similarity，SSIM)等进行去模糊质量评价,而实际很多图像的处理是没有原始清晰图像的[14]。本文所提算法改进现有的去模糊过程,引入无参图像质量评价,增加反卷积后图像质量评价和优化过程,使得单幅模糊图像在没有清晰参考图像的情况下复原出最优图像质量。

本文方法主要解决高速运动图像的去模糊,并实时应用在轨道缺陷检测系统中[15],为此提出一种基于自然场景统计融合质量评价的方法，对图像反卷积后的图像进行质量评价并再优化。具体算法过程见图1。

图1 运动去模糊算法设计

1 运动图像退化模型及空间变换

在获取数字图像过程中由于各种复杂原因使得图像质量下降(退化),这些退化包括由光学系统、大气湍流效应、运动等造成的图像模糊、畸变、失真以及源自电路和光学因素的噪声。本文主要针对目前在线监测的视频及图像中产生的模糊,如车载相机安装在固定的平台,模糊主要由相机运动与场景的相对运动产生。

模糊图像是由原始清晰图像与模糊核卷积而成[4-6],在车载相机中,图像通过安装在车辆底部的相机来采集获取。如图像获取是通过安装在轨道缺陷检测系统中的相机,由于机车运动时,相机在曝光时间内产生位移,因此采集的图像汇集了采集点邻域内的图像信息。

( 1 )

式中：g(·)为目标场景的像素值；(x,y)为图像像素空间位置；n(x,y)为(x,y)处的噪声；D(·)为t时刻(x,y)位置的某一邻域；(u,w)为D(·)中的一点。

以运动方向为坐标轴x,当主光轴垂直于运动方向,机车以速度v运行时,假设噪声n(x,y)=0,则相机所获得的模糊图像为

( 2 )

由此，式( 2 )的离散形式为

( 3 )

对于整幅图像来说,令

则式( 3 )可写成

A·G=B

( 4 )

分析矩阵A可知,该矩阵的秩为n,变量个数为n+l-1,方程组有l-1个自由基,有无穷多个解,该问题是一个不定解问题。

我们讨论增加l-1个方程组,将矩阵A扩展为

( 5 )

从式( 5 )可以看出,模糊图像反卷积不定解的问题转变为以S为自变量的非奇异线性方程组的求解问题,且该方程组只有唯一解。

分析式( 5 ),S取值为G的前项累积和,因此可以通过线性预测和梯度加权法预测其初值,即

( 6 )

式中：β为线性插值和梯度预测的权值。

2 图像直接反卷积及图像自然统计分布规律

2.1 图像直接反卷积问题

一般认为,图像的模糊过程为原图像与未知的模糊核卷积的过程,而图像去模糊则为反卷积过程,但这个反过程是病态的[4-5],复原图像会出现一些杂痕。文献[10]认为这种杂痕是由不准确的模糊核及噪声等引起的。本文研究的高速运动模糊形成过程中,模糊图像边界是由图像边缘和超边缘信息复合形成,即实际采集的图像边界都是有未知信息的,所以直接进行卷积就会出现大面积条纹状的杂痕，见图2。

图2 模糊图像直接反卷积结果

针对该问题，本文通过式( 6 )预测边界块初始信息的方法再进行反卷积,以补充图像在模糊卷积过程中消失的边界块。将未知信息单元作为未知变量,根据图像自然统计特性的算法进行去模糊处理,得到统计特性最佳的边界及其清晰图片。

2.2 图像自然统计特性

在图像复原问题中,一个最为广泛的图像先验知识就是自然图像在梯度空间中具有的规律分布。自然图像中梯度的分布在0处相当于长尾分布,这与标准的高斯分布有较大偏差。即对于一幅自然图像而言,其梯度值接近于0的像素点相对于拥有其他梯度值的像素点在图像中所占据的比例相对较大,保证了相邻图像灰度的一致性。文献[16]认为自然图像的梯度分布不完全符合拉普拉斯分布,而是符合一种超拉普拉斯。通过大量的研究和实验表明[8-9，16],图像的自然统计特性可表示为

( 7 )

其对数统计分布为

( 8 )

ζ值不同表示不同的模型,若ζ为1,表示拉普拉斯模型；若ζ为2,表示高斯模型；若ξ为0.66,则表示超拉普拉斯模型。其统计规律见图3。

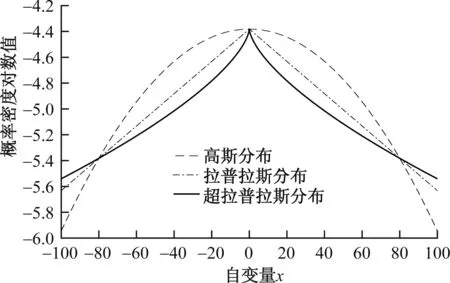
图3 图像自然统计分布规律

本文提出的基于图像列灰度一致性的方法也源于对自然图像统计的特性,不同于大多数方法采用梯度作为衡量标准,本文通过图像列灰度差作为图像去模糊优化评价指标,减少图像矩阵计算量。

3 图像反卷积后优化建模及算法设计

基于上述的自然图像特性分析,统计了上万幅自然图像的相邻列差分布,其规律大致一致,见图4中图像相邻列像素灰度差异统计,自然清晰图像的相邻列灰度相差较小,而模糊图像的相邻列灰度相差较大。这同文献[8-9]所述的自然图像梯度服从长尾分布具有相似的性质,而失真变形的图像则不同于此分布。

图4 图像相邻列灰度差统计

图4分别用3个段来表示相邻列差值分布,即列差为0,1～10以及大于10的分布情况。图4中蓝色点代表自然清晰图像相邻列灰度差绝对值分布情况,其分布集中在较小值范围内。其绝对差值在0的主要分布区间为45%～65%,范围在1～10的主要分布区间为30%～45%,大于10的主要分布区间为0%～10%。图4中红色的点则表示模糊的图像分布情况,从图像中可以看出,图像相邻列灰度差出现两极分化现象,大部分向0靠拢,绝对差在0的比例超过90%；同时会出现一些列差较大的情况,有90%以上列灰度差超过10,这就是图像上得到的条纹分界线。我们主要关注列差在0～10范围内的点,由此构建列灰度α置信一致性指标cgpc。

( 9 )

式中：Nα为去除最大的α%像素点后剩下的点集；Ci(x)和Ci+1(x)分别为前后两列的灰度值；α为单边置信均值；k为误差允许值。整幅图像的灰度α置信一致性指标为

(10)

从图5可以看出,当反模糊过程中灰度值由0变化到255时,整幅图像的CGPC值有两种状态:保持不变和单下凸。即当该变量值处于排除的α范围内时,CGPC保持不变；当处于排除范围外时,CGPC值在图像最清晰时最小。

图5 任一自变量与CGPC的关系

现有的许多图像复原优化算法都没有加入图像质量评价环节,而是用PSNR、RMS及SSIM等这些有参的图像评价指标验证算法的有效性,但实际上很多模糊图像并没有原始清晰图像[19]。本文采用无参的图像质量评价指标BRISQUE应用在图像反卷积的优化算法中。从图6可知BRISQUE在像素点灰度变化范围内具有整体最优特性,并且该方法对处理大尺寸图像具有实时的效果。

图6 任一自变量与BRISQUE的关系

观察图7(图5和图6中第一个统计图的局部放大图)可得,BRISQUE特征在局部细节中存在非单调性,即统计特征曲线存在波动,而本文的CGPC统计特征曲线单峰光滑。

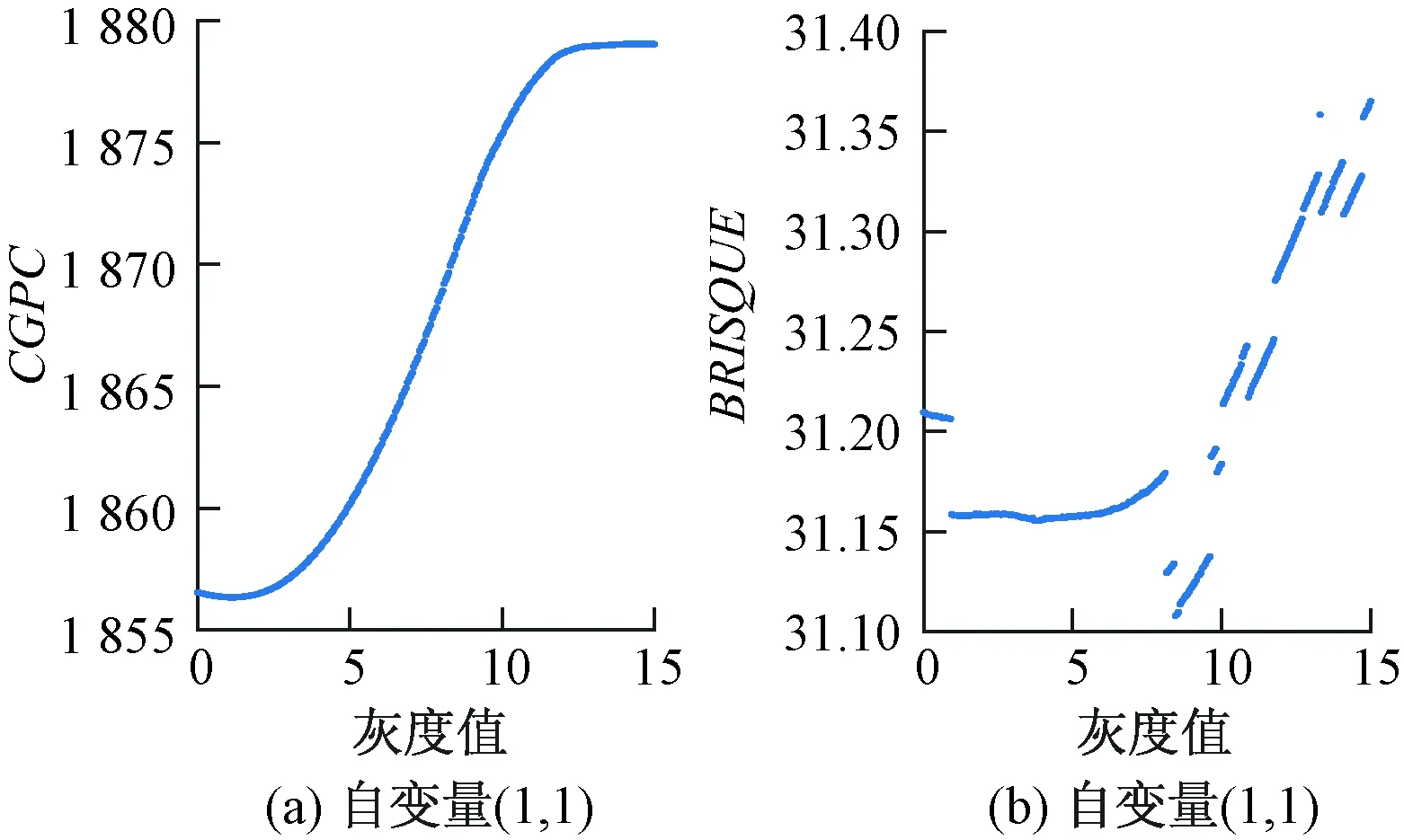
图7 评价指标CGPC和BRISQUE局部放大图

为确保去模糊图像最优化方法的单调性,将该问题分两步求解:

Stelp1粗优化,以BRISQUE的图像质量评价指标最小为目标,采用遍历方法得到最优解的大致范围。

Stelp2精优化,根据CGPC对估计范围进一步优化,提高遍历步长,从而求得全局最优值。

4 实验结果

本文主要解决由于高速运动的轨道图像导致的运动模糊问题,为了比较和验证算法的适用性,选用标准图像和实际轨道模糊图像两种类型的图像进行测试,见图8。选用应用广泛的Lena图像,其像素为1 024×1 024作为标准图像测试,图8中第1行的图像模糊长度较短，即l=5,通过与其他算法比较可知,对于模糊较轻的图像各种算法都能取得较好的效果。但对于模糊长度较严重的情况下，即l=25时(图8第2行),其他3种算法都出现不同程度的振铃效应,采用主观的质量评价方法,基于列统计并对图像复原后的质量再进行评价和优化的方法取得的视觉效果明显更优。图8第3行为实际采集的轨道模糊图像,通过本文方法计算得到模糊长度为31像素,本文算法处理后能够得到更清晰的轨道图像。

针对解决高速运动的轨道图像导致的模糊问题,本文在合作方实验轨道上进行系统测试,对轨道缺陷检测系统采集的图像先进行去模糊处理,并从中选取有缺陷的图像的去模糊效果图像,见图9,图9(a)这8幅图分别为在拍摄时存在的不同程度的模糊图,图9(b)为图9(a)中分别相对应的去模糊图。采用本文方法对图9(b)中8幅图估计的模糊长度分别为12、15、8、16、5、3、20、13像素,去模糊后效果如图9(b)所示,从主观上观测，图像明显清晰化。

图8 与现有的方法进行人工及实际模糊图像复原效果对比

图9 采集的轨道缺陷图像去模糊

通过比较分析及图像处理实时性的要求,选用基于BRISQUE的方法来进行图像质量评价及优化,即BRISQUE评价指标值越低图像复原质量越高。通过系统采集的其中50幅轨道模糊图像进行实验,见图10。其BRISQUE指标相对较高即图像质量不高,通过与现有实验效果较好的文献[8]比较,大多数情况下本文算法的BRISQUE值比文献[8]的方法要低,即去模糊效果更好。而有部分图像的评价值两者相同,说明本文方法和文献[8]方法取得的去模糊效果一致。进一步比对实际图像发现,取得效果一致的图像的模糊程度较轻,而本文方法针对前向运动导致的严重模糊效果更好。