弯度对风力机翼型气动噪声特性的影响

孙振业 陈昕乐 刘宇新

摘要：指出了陆上风电装机向着低风速区和分散式发展，风力机距离居民区越来越近，风力机的噪声问题日趋严重，需要在风力机的设计阶段对气动噪声进行研究与控制。翼型是风力机叶片的基本元素，是风力机功率及噪声性能的基石。弯度对翼型的气动性能有显著影响，因而也必然影响气动噪声源。选取NA-CA系列翼型作为研究对象，翼型的最大厚度及最大厚度的弦向位置、最大弯度的弦向位置相同，而最大弯度不同。采用经典的翼型分析软件XFOIL计算了上述翼型的升阻力系数、半经验模型计算气动噪声源水平，以研究最大相对弯度对气动和噪声性能的影响。结果表明：在小攻角范围内，翼型的升力系数、升阻比随着最大相对弯度的增加而增加，大攻角时升阻比随着最大弯度的增大而减小。翼型最大弯度增加会使得压力面尾缘噪声在低频段内减小;在整个频率段内，边界层分离噪声随着最大弯度的增加向低频区移动。

关键词：风力机;气动噪声;翼型;弯度

中图分类号：TK89 文献标识码：A 文章编号：1674-9944（2019）22-0135-03

1 引言

风能已经成为我国及世界可再生能源的重要组成部分。我国风能发展起步晚，但是发展迅速，中国已经成为风电大国。但是风能领域的基础科研起步晚、投入小，导致中国还不是风电强国。快速的风电发展及装机，也产生一些附带问题。随着风力机的广泛运用以及大型化，分散式装机及风电场距离居民区越来越近，风力机的气动噪声对附近的居民及生物产生了困扰。风力机的气动及噪声性能的基石是翼型[1]。进行钝尾缘改型和增大相对弯度是两种提升翼型气动性能的有效措施。钝尾缘改型在结构上使叶片能承担更大的压力载荷，在气动特性方面提高了升力系数[2]。而适当增大相对弯度同样也可以提高翼型升力和风能利用系数。对翼型进行气动外形优化，得到的高升阻比翼型往往具有较大的相对弯度。因而，提高风力机性能的重要途径是采用弯度较大的翼型[3]。同时相对弯度对风力机的气动噪声都也起着不可忽视的影响。风力机的噪声主要由两部分构成：机械噪声和气动噪声[4]。前者是由于机械设备的振动等引起。后者是现代商用风力机噪声的主要部分，包含低频噪声、湍流入流噪声、翼型自噪声[4]。低频噪声是旋转叶片与塔架或风剪切相互作用产生，由于人耳对其不太敏感，所以在A加权噪声频谱图上，此类噪声对A加权声功率级贡献较少。湍流入流噪声是叶片与入流湍流涡相互作用产生。翼型自噪声主要包括：叶尖涡噪声和尾缘钝厚度导致涡脱落产生的噪声等5种[5]。上述3种翼型气动噪声中，翼型自噪声通常占主导地位，而最大相对弯度对冀型气动性能的影响比较大，因此需要研究最大相对弯度对翼型噪声的影响。关于风力机气动噪声的研究主要通过实验及数值模拟实现。朱卫军[6]将可压缩NS方程分离成不可压缩流动方程和无粘声学方程两个部分，使得计算噪声仿真计算效率得以提高。李仁年等[7]数值研究了弯度对风力机翼型原型气动特性的影响，结果显示在一定范围内大弯度翼型有更高的升、阻力系数和升阻比。申振华等[8]通过压力面的“涡轮化”改造增加了翼型弯度，并进行了风洞对比实验，研究表明翼型“涡轮化”可以显著提高风力机的风能利用系数。

2 预测模型

美国可再生能源实验室的Brooks，Pope和Marco-lini提出了BPM半经验翼型噪聲预测模型，此模型是根据一组弦长不同的NACA0012翼型的大量气动和声学实验数据而得，给出了5种翼型自噪声的半经验模型。采用BPM模型可以快速地完成噪声预测，比采用数值仿真或实验方法节省大量时间，可被用于翼型的优化设计。BPM模型在附着或者小分离流动状态下的精度可以达到实际工程要求，被广泛使用。但风力机叶片上的翼型形状、弦长、入流状态等与BPM模型建立时的实验状态不同，因而采用BPM模型中同一种半经验公式来模拟不同的翼型边界层参数，会使降低对风力机翼型噪声的仿真精度。因此，需要对经典BPM模型进行修正，使其适用于不同的翼型、不同的工况。基于BPM半经验模型，Lowson研究了模型中边界层厚度参数的影响。Zhu等[9]基于翼型噪声预测半经验模型，引用叶素动量理论，并采用了一种新的叶尖修正技术，从而提高了该模型的准确性。模型对湍流边界层尾缘噪声、分离流噪声、层流边界层涡脱落噪声、钝尾缘噪声、叶尖涡噪声都进行计算，详细介绍可参考文献[9，10]。

3 翼型最大相对弯度的影响

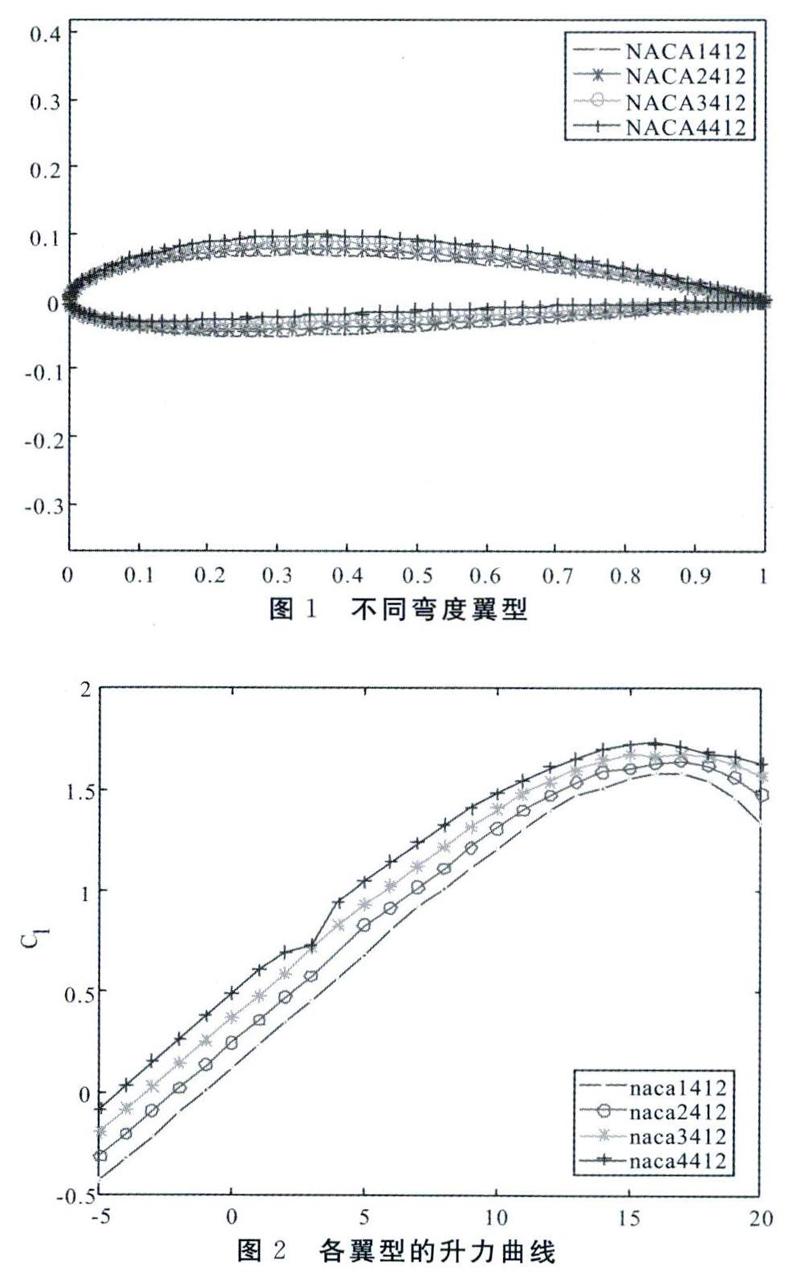
以NACA4数字系列翼型为研究对象，选取N A-CA1412，NACA2412，NACA3412，NACA4412四种不同翼型。翼型的最大相对厚度、最大厚度所在位置、最大弯度所在位置基本相同，最大相对弯度不同。翼型的气动性能采用XFOIL软件计算，该软件求解速度快，耦合性良好[19]。默认雷诺数为，马赫数为0.15，攻角在一5°～20°范围内。在计算翼型噪声时，采用扬州大学开发的风力机翼型噪声源仿真软件。各参数均为默认值：来流风速80m/s，接收距离1m，接收角度90°，翼型展长为1m，翼型弦长C=1m，入流攻角5”，翼型表面光滑，锯齿角度-2.5°，锯齿的长和宽分别为0.15m和0.25m，声速为340m/s，粘性系数为0.000015Pa·S。

3.1 各其型气动性能对比

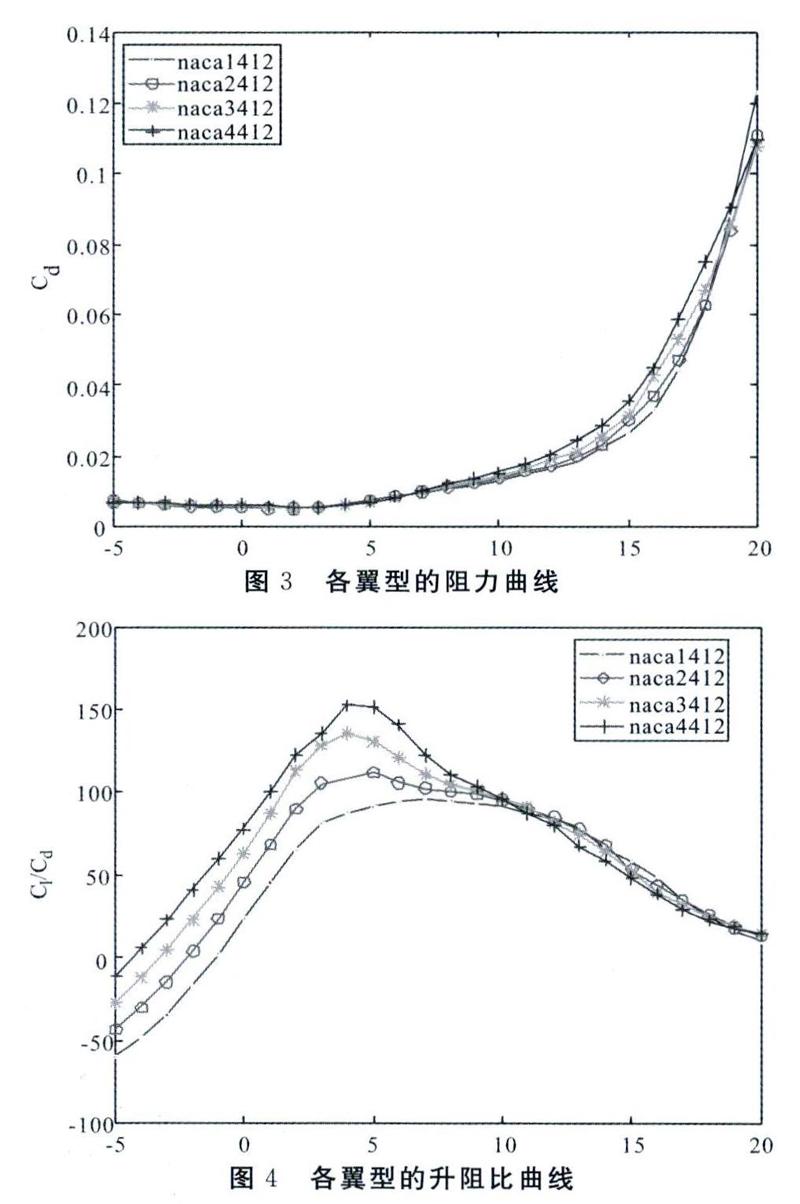
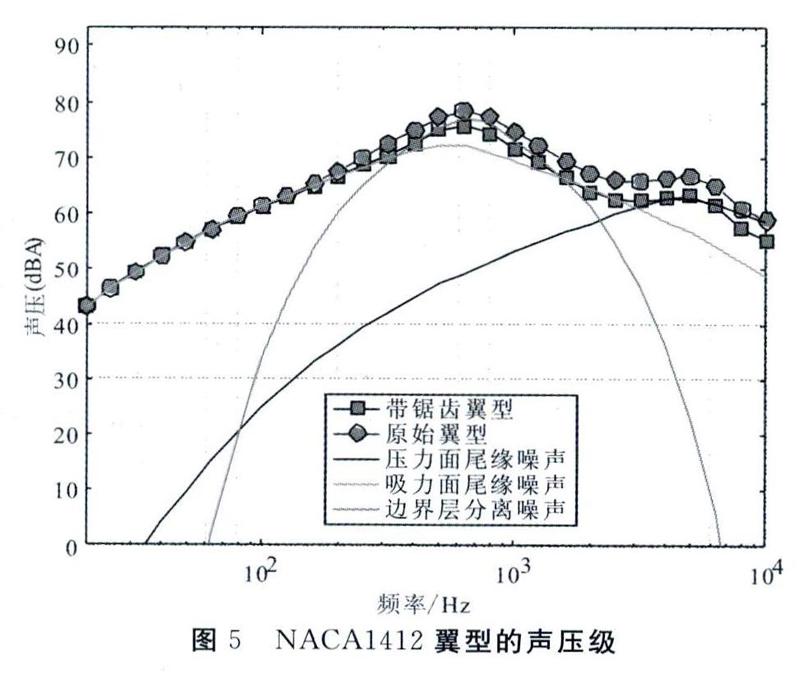
不同弯度翼型的外形对比如图1所示。在自由转捩工况下，计算攻角范围为-5°～20°时各翼型的升力、阻力系数和升阻比，结果对比分别如图2一图4所示。由于人耳对不同频率的敏感性不同，为了反映人耳实际感受到的声音大小，引入了A加权法。A加权声级的测量单位为dB。以下的声压级图谱中都做了A加权算法。

由图2可知，在-50°～20°攻角范围内，翼型的升力系数随着最大相对弯度的增加而增加，且增加的趋势基本相同。由图3可知，攻角小于7°时，不同弯度的翼型在相同攻角下的阻力系数基本相同;攻角大于7°时，翼型的阻力系数随着弯度的增加而增加。由图4可知，攻角小于10°时，翼型的升阻比随着弯度的增加而增加，趋势较为明显;当攻角大于10°时，翼型的升阻比随着攻角的增大而减小，且对于不同弯度的翼型，各升阻比相差不大。