基于企业环保目标和消费者环保意识的闭环供应链网络决策研究

刘阳 张桂涛

摘要

随着生态文明与可持续发展理念的日益普及，企业在其运营过程中不仅要追求经济利益目标，而且应兼顾环境保护目标。在此背景下，本文针对多原材料供应商、多制造商、多零售商、多回收商与多个需求市场组成的闭环供应链网络，构建各类企业成员利润最大化与碳排放量最小化双重决策目标下的优化问题，然后运用变分不等式和对偶理论给出各层达到均衡的条件，并获得整个闭环供应链网络均衡模型。采用修正投影收缩算法设计模型求解程序，最后结合数值算例对环保目标权重系数和消费者低碳环保意识等重要参数进行了比较静态分析，获得了一些有益的管理学启示。结果表明：当某类企业的环保目标权重增加时，将给该类企业带来经济利益和环保绩效的双重改善;当所有企业的环保目标权重同时增加时，环保绩效明显改善，而企业经济效益的变化存在不一致现象，且其利润协调较为复杂;尽管消费者低碳偏好意识的提升能够改善环保绩效，但却使各网络成员与闭环供应链网络的整体利润降低。以上所得结论对闭环供应链研究与政府低碳环保政策的设计具有一定的借鉴意义。

关键词闭环供应链网络;环境保护目标;Nash均衡;多目标决策;消费者环保意识

中图分类号F252

文献标识码A文章编号1002-2104（2019）11-0071-11DOI：10.12062/cpre.20190707

十九大报告指出：坚持实行可持续发展战略，坚持走绿色发展道路，制定并执行严格的环保法;人与自然是协调共存的，绿水青山就是金山银山，我们要爱护环境、呵护自然，过低碳绿色生活。自然环境是人类生存的依托和载体，但人类的个体活动目标和环保目标通常存在不一致。自从人类进入工业化社会以后，科技与经济飞速发展的同时也使得废弃物和污染物数量急速上升，目前已对环境产生不可逆转的影响，突出表现为恶劣天气频繁出现、海平面上升、病虫害增加等方面，而这些现象也威胁到了人类自身的生存。因此，在可持续发展理念指导下，如何通过有效的产品回收再利用并减少碳排放，以期同时实现企业的经济目标与环保目标是各国政府、企业决策者和研究人员关注的重要议题。

本文以多供应商、多制造商、多零售商、多回收商和多需求市场组成的闭环供应链为研究对象，同类成员间进行Nash博弈，各类企业均同时考虑碳排放量最小化与利润最大化的双重目標，运用变分不等式等理论建立闭环供应链网络均衡决策模型，针对环保目标权重与消费者低碳偏好意识等重要参数进行算例分析，所得结论对企业的现实决策和政府低碳环保政策的设计具有一定的借鉴意义。

1文献综述

我国东部经济发达地区饱受雾霾等环境灾难的困扰[1]，对经济发展和人们生活造成很大影响。在此背景下，迫切需要企业及相关领域改变传统发展方式，企业实现经济目标必须满足生态环保目标的约束。要实现生态环境保护的目标，一方面需提高旧产品的回收再制造率，以减少其中的有害物质对环境的负面影响，同时促进资源的循环利用与可持续发展;另一方面则需降低供应链运营过程中各企业节点的碳排放量。

企业的回收再制造活动与其传统正向供应链相结合而形成闭环供应链系统[2]。闭环供应链中不仅包含传统供应链中的供应商、制造商、零售商以及消费者，而且还可能包括第三方回收企业。此外，在当前市场竞争日趋激烈的背景下，同类成员之间的竞争不可避免，如制造商间的竞争或零售商间的竞争等;异类成员间的交叉合作现象也日益普遍化，如同一供应商可向多个相互竞争的制造商提供原材料，同一制造商也可通过多个相互竞争的零售商分销其产品等。故在现实中闭环供应链通常是以具有复杂竞合关系的网络形式而存在。本文正是以第三方回收模式下的闭环供应链网络为研究对象，考虑其中的网络成员同时追求经济利益最大化与碳排放量最小化的双重目标，在此基础上分析网络成员的均衡行为与利润分配问题。与本文相关的研究主要在低碳环境下再制造闭环供应链的定价与生产/再制造决策、闭环供应链网络均衡以及消费者环保意识三个方面。

近二十年来，再制造闭环供应链是物流与供应链领域的研究热点之一，目前在学界已取得丰硕的研究成果，读者可参阅三篇较有影响力的综述文献[3-5]。此处主要给出与企业低碳环保决策直接相关的闭环供应链领域成果。Chang等[6]研究了碳交易机制下垄断制造商的生产/再制造策略。Yenipazarli等[7]建立Stackelberg主从博弈模型探讨了监管机构的碳税政策对企业新产品与再制造产品差异定价与生产策略的影响，并将模型拓展至碳交易情形中。Bazan等[8]针对由两级闭环供应链，研究了经典库存模型与供应商管理库存（VMI）两种模式下的系统碳排放量与能源消耗问题。He等[9]针对包含产品制造商、实体零售商与在线零售商的双渠道闭环供应链，探讨了消费者的搭便车行为对系统碳排放量的影响。聂佳佳等[10]针对零售商回收模式下的闭环供应链系统，比较了有无碳排放约束下的旧产品回收率、渠道成员利润以及碳排放量，着重考察政府的碳排放奖惩力度对均衡决策与碳排放量的影响。李辉等[11]分别在制造商主导、零售商主导、Nash均衡及集中式决策四种权力结构下构建了闭环供应链博弈（优化）模型，比较了不同结构下的产品定价、低碳宣传努力程度、回收率、碳减排水平与渠道成员利润。李进等[12]建立机会约束多目标模糊规划模型研究了以最小化总运营成本与碳排放量为双目标的闭环供应链网络设计问题，并提出了求解模型的交互式约束算法。其他相关研究还包括文献[13-15]等。以上文献在企业的碳减排行为与碳排放量核算方面对本文具有重要的借鉴意义，但其均围绕简单的线型闭环供应链开展研究，而如前所述，现实中的闭环供应链系统是一个复杂的供应链网络。

闭环供应链网络Nash均衡问题拓展于Nagurney等[16]最早对传统正向供应链网络均衡问题的研究，如围绕不同的闭环供应链回收模式、再制造产品特性与销售渠道等方面进行建模分析。Hammond等[17]和Yang等[18]分别针对制造商回收的二级供应链网络与第三方回收的五级供应链网络构建了闭环供应链网络均衡模型。Qiang[19]将产品设计阶段的可再制造水平作为决策变量，探讨了闭环供应链网络中两相互竞争的制造商对新产品与再制造产品的差异定价、可再制造水平与生产/再制造批量联合决策。张桂涛等[20]研究了考虑消费者对实体销售渠道与电子直销渠道具不同偏好情形下的有限多周期闭环供应链网络均衡问题。但文献[16-20]未涉及环境保护因素，即所有网络成员均以经济利润最大化作为决策目标。将环保因素与碳排放约束引入至（闭环）供应链网络均衡的研究相对较少。Nagurney[21]将企业的经济目标与环保目标相结合，构建了决策者具有双重目标的供应链网络均衡模型。马秋卓等[22]研究了三级供应链网络中的产品最优定价与产量决策问题，其中不同网络成员各自的碳交易中心组成一个碳交易市场。Zhang等[23]针对政府的两种强制性碳减排机制（周期性碳减排约束与全局性碳减排约束），在多周期背景下构建了第三方回收模式的闭环供应链网络均衡模型。杨玉香等[24]研究了具有环境指标的多准则闭环供应链网络均衡问题，但其假定零售商从事产品回收，且未考虑消费者环保意识对网络均衡决策与成员利润的影响。

fMm=fMm（q2）：制造商m使用原材料时的生产成本函数，与q2有关;

fum=fum（qu）：制造商m使用废旧品时的再制造成本函数，与qu有关;

csm=csm（qsm）：供应商s与制造商m间的交易成本函数;

cmn=cmn（qmn）：制造商m与零售商n间的交易成本函数;

cnk=cnk（qnk）： 零售商n与需求市场k间的交易成本函数;

cKnk=cKnk（qnk）： 需求市场k与零售商n间的交易成本函数;

cuim=cuim（quim）：回收商i与制造商m间的交易成本函数;

cuki=cuki（quki）：回收商i从需求市场k回收废旧品的交易成本函数;

cm（qum）：制造商m处理废旧品成本函数;

cn（Q2）：零售商n从事销售活动的成本函数;

dk（ρ;θ，β）：需求市场k处的产品需求函数，其受本市场和其他市场中消费者支付价格（价格向量ρ）的影响，同时受消费者低碳环保（低碳环保因子θ∈[0，1]）和产品生产、交易过程中的碳排放量（碳排放向量β）的影响，其中涉及参数β0为行业标准水平，易知当碳排放量高于该标准时，其市场需求低于仅存在价格竞争时的水平，反之则高于仅存在价格竞争时的水平。ε1、ε2和ε3分别为对应因素的影响因子。

（4）内生价格变量如下：

ρrsm：供应商s与制造商m间原材料交易价格;

ρmn：制造商m与零售商n间交易价格;

ρuki：需求市场k与回收商i间废旧产品交易价格;

ρnk：零售商n与需求市场k间交易价格;

ρuim：回收商i与制造商m间废旧产品交易价格。

3模型建立

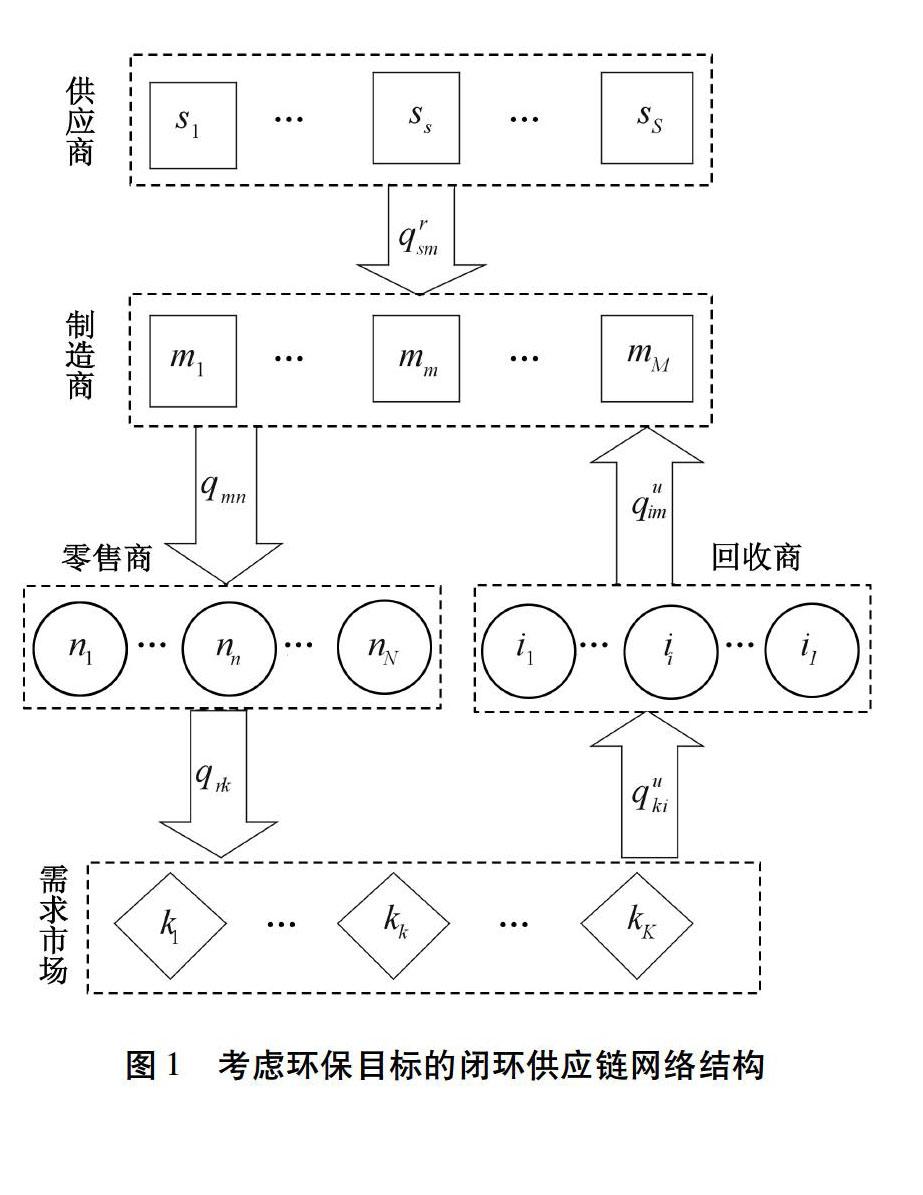
供应商层向制造商层供应原材料，在产品生产和交易过程中产生二氧化碳。新产品生产过程中产生二氧化碳，制造商与零售商的交易活动、零售商与需求市场的交易活动中也产生二氧化碳。需求市场的消费者根据价格等因素决定是否购买，其需求量受产品价格等因素高低的影响。下文中变量上标“*”表示对应变量的均衡解。

3.1供应商层的最优行为及均衡条件

各供应商生产一定数量的原材料，以满足各制造商的需要。在供应商生产和交易过程中，均排放二氧化碳。各供应商以自身利润最大化为决策目标，供应商之间开展非合作Nash博弈。供应商s利润最大化目标可表示为：

maxπs=∑Mm=1ρrsmqrsm-fSs（q1）-∑Mm=1csm（1）

s.t.qrs≥∑Mm=1qrsm（2）

同时，供应商s还考虑碳排放量最小化目标，根据前述符号，该目标可表示为：

mines=β1sqrs+β2sm∑Mm=1qrsm（3）

为了处理方便，把两个目标决策问题转化为单目标决策问题。为此，类似于Nagurney等[21]的研究，需引入权重因子，来衡量两个决策目标之间的相对重要程度。为简单起见，假设利润目标权重为1，碳排放量目标权重为α1，且一般有α1∈R+。由此，供应商s的总目标函数可表示为：

maxhs=∑Mm=1ρrsmqrsm-fSs（q1）-∑Mm=1csm-α1tc（β1sqrs+β2sm∑Mm=1qrsm）（4）

同时供应商的决策应满足约束（2）。令其对应的Lagrange乘子为μs，则μ=[μs]S×1∈RS+。根据上述交易函数和生产函数均为连续可微凸函数的假设，优化问题（4）可以转换为变分不等式，即确定（q1*，Q1*，μ*）∈ΩS，满足：

∑Mm=1[fSs（q1）qrs-μ*s+α1tcβ1s]×[qrs-qr*s]+∑Ss=1∑Mm=1[c*smqrsm+μ*s-ρr*sm+α1tcβ2sm]×[qrsm-qr*sm]+∑Ss=1[qr*s-∑Mm=1qr*sm]×[μs-μ*s]≥0（5）

（q1，Q1，μ）∈ΩS，其中ΩS=RS+SM+S+。

根据式（5）第一项，当qr*s>0，即在均衡状态下，根据变分不等式和互补的等价关系，μ*s=fSs（q1）qrs+α1tcβ1s，表明μ*s等于供应商的原材料生产成本与α1tcβ1s的和;根据第二項，当qr*sm>0时，即存在交易的情况下，ρr*sm=c*smqrsm+μ*s+α1tcβ2sm=c*smqrsm+fSs（q1）qrs+α1tcβ1s+α1tcβ2sm，交易价格等于边际交易成本、边际生产成本和生产与交易环节碳排放因子、惩罚与权重的乘积之和。也就是说，通过交易关系，供应商把成本转移到下游的制造商。

3.2制造商层的最优行为及均衡条件

制造商从供应商处采购原材料，从回收商处购买废旧品，同时开展新产品生产和再制造品生产，对于消费者而言，两种产品无差别。对于生产的产成品，通过各零售商销售给需求市场。制造商m的利润最大化目标函数可表示为：

max πm=∑Nn=1ρmnqmn-fm（qrm）-fMm-fum-∑Nn=1cmn-cm（qum）-∑Ii=1ρuimquim-∑Ss=1ρrsmqrsm（6）

s.t. βrqrm+βuqum≥∑Nn=1qmn（7）

qum≤∑Ii=1quim（8）

qrm≤∑Ss=1qrsm（9）

约束（7）的含义是：制造商m与所有零售商的产品交易总量不能高于通过原材料制造的新产品和通过废旧品生产的再制造品数量之和。约束（8）的含义是：制造商m再制造利用的废旧品数量不高于从各回收商购买的废旧品数量。约束（9）的含义是：制造商m新产品生产过程利用的原材料数量不高于从供应商层购买的原材料数量。

制造商在新产品的生产过程和与零售商的交易过程中，产生二氧化碳。制造商除了利润最大化目标外，还考虑二氧化碳排放量最小化目标，该目标可表示如下：

min em=β3mqrm+β4mn∑Mm=1qmn（10）

与供应商层的转换方式相类似，把制造商的利润权重设定为1，引入一个因子α2，且有α2∈R+，表示制造商环境保护目标的权重，制造商m的决策问题转化为单目标问题表示如下：

max hm=∑Nn=1ρmnqmn-fm（qrm）-fMm-fum-∑Nn=1cmn-cm（qum）-∑Ii=1ρuimquim-∑Ss=1ρrsmqrsm-α2tc（β3mqrm+β4mn∑Mm=1qmn）（11）

同时制造商m满足约束（7）、约束（8）和约束（9），假设约束（7）、约束（8）和约束（9）对应的Lagrange乘子分别为η1m、η2m和η3m，且η1=[η1m]M×1、η2=[η2m]M×1、η3=[η3m]M×1。

根据交易函数和生产函数均为连续可微凸函数的假设，优化问题（11）可转换为变分不等式，即确定（qr*，qu*，Q2*，Q4*，η*1，η*2，η*3）∈ΩM，满足：

∑Mm=1[fMmfm（qr*）qrm+qrm-βrη*1m+η*3m+α2tcβ3m]×[qrm-qr*m]+∑Ss=1∑Mm=1[ρr*sm-η*3m]×[qrsm-qr*sm]+∑Mm=1[fumqum+cm（qu*m）qum-βuη*1m+η*2m]×[qum-qu*m]+∑Mm=1∑Nn=1[c*mnqmn+η*1m-ρ*mn+α2tcβ4mn]×[qmn-q*mn]+∑Ii=1∑Mm=1[cu*imquim-η*2m+ρu*im]×[quim-qu*im]+∑Mm=1[βrqr*m+βuqu*m-∑Kk=1q*mn]×[η1m-η*1m]+∑Mm=1[∑Ii=1qu*im-qu*m]×[η2m-η*2m]+∑Mm=1[∑Ms=1qrsm-qrm]×[η3m-η*3m]≥0（12）

（qr，qu，Q2，Q4，η1，η2，η3）∈ΩM，其中ΩM=RM+M+MN+IM+M+M+M+。

由式（12）的第1項可知，当qr*m>0时，即在均衡状态下，根据变分不等式和互补的等价关系，η*1m=1βrfMmqrm+fm（qr*）qrm+η*3m-α2tcβ3m，即η*1m等于制造商购买原材料和生产新产品的边际成本减去权重因子与生产单位产品的碳排放量、惩罚之积后，再除以βr;由式（12）的第3项可知，当q*mn>0时，ρ*mn=c*mnqmn+η*1m+α2tcβ4mn=c*mnqmn+1βrfMmqrm+fm（qr*）qrm+η*3m-α2tcβ3m+α2tcβ4mm。与前文对供应商的分析相类似，通过交易，制造商把有关的生产成本、交易成本和政府惩罚引起的成本等方面转移至零售商。另外，通过式（12）的第2项和第4项可知，回收的废旧品价格通过η*2m影响η*1m，进而影响了交易价格ρ*mn，因此交易价格中实际上还包含回收价格。

3.3零售商层的最优行为及均衡条件

制造商将产品批发给零售商，零售商经过自己的渠道让顾客购买产品。各零售商之间进行非合作Nash博弈，则零售商n的利润最大化目标函数可表示为：

max πn=∑Kk=1ρnkqnk-∑Kk=1cnk-cn（Q2）-∑Mm=1ρmnqmn（13）

s.t. ∑Mm=1qmn≥∑Kk=1qnk（14）

约束（14）的含义是：零售商销售给各需求市场的产品总量不能高于从各制造商购买的产品数量。

同时，考虑环境保护目标，各零售商以交易过程中的碳排放量最小为另一决策目标，根据前述符号，该目标可表示为：

min en=β5n∑Kk=1qnk（15）

与供应商层和制造商层的转换方式相类似，把零售商的利润权重设定为1，引入一个因子α3表示零售商环境保护目标的权重，且有α3∈R+，零售商n的决策问题转化为如下单目标问题：

max hn=∑Kk=1ρnkqnk-∑Kk=1cnk-cn（Q2）-∑Mm=1ρmnqmn-α3tcβ5nk∑Kk=1qnk（16）

同时需满足约束（14）。假设约束（14）对应的Lagrange乘子为δn，且δ=[δn]N×1。则优化问题（16）可转换为变分不等式，即确定（Q2*，Q3*，δ*）∈ΩN，满足：

∑Mm=1∑Nn=1[cn（Q2*）qmn-δ*n+ρ*mn]×[qmn-q*mn]+

∑Nn=1∑Kk=1[c*nkqnk+δ*n-ρ*nk+α3tcβ5nk]×[qnk-q*nk]+

∑Nn=1[∑Mm=1q*mn-∑Kk=1q*nk]×[δn-δ*n]≥0（17）

（Q2，Q3，δ）∈ΩN，其中ΩN=RMN+NK+N+。

根据变分不等式和互补的等价关系，由式（17）第1项知当q*mn>0时，δ*n=cn（Q2*）qmn+ρ*mn;由式（17）第2项知，当q*nk>0时，ρ*nk=c*nkqnk+δ*n+α3tcβ5nk=cn（Q2*）qmn+ρ*mn+c*nkqnk+α3tcβ5nk。也就是说，制造商与零售商间的交易价格通过零售商与需求市场间的交易，对需求市场也产生影响，如果制造商与零售商间的交易价格增加，则零售商与需求市场间的交易价格也增加。

3.4需求市场层的最优行为及均衡条件

在多个消费市场内，顾客会通过考虑零售商收取的价格决定是否购买产品;产品经过使用，部分失去使用价值而形成废旧品，废旧品可以通过回收环节到制造商处进行再制造。回收过程中，回收商先给出废旧品回收价格，消费者据此决定是否把废旧品卖给回收商。根据文献[16]，对于零售商提供的产品，消费者愿意支付的价格与零售商收取的价格之间满足互补关系：

ρ*nk+cK*nk=ρ*k，q*nk>0≥ρ*k，q*nk=0（18）

同时，需求市场中产品的需求量与供给量之间的关系满足：

dk（ρ*;θ，β）=∑Nn=1q*nk，ρ*k>0≤∑Nn=1q*nk，ρ*k=0（19）

在回收过程中，引入回收厌恶函数用以表示消费者在废旧品回收过程中产生的负效用。实际中，回收商回收的废旧品数量越多，给消费者带来的价值损失越多，消费者的负效用就越大，因此消费者希望获得的回收价格就越高。回收厌恶函數为回收量的单调增函数，假设其形式为αuk（Q5）。类似于文献[17，18]，有：

αuk（Q5*）=ρu*ki，qu*ki>0≥ρu*ki，qu*ki=0（20）

且需求市场中的回收量有如下约束：

∑Ii=1qu*ki≤rk∑Nn=1q*nk（21）

约束（21）表明，回收的废旧品数量不能超过需求市场中可回收废旧品数量之和;而需求市场消费者购买的产品中，既包含新产品，也包含再制造品，再制造品每经过一次再制造后，可回收数量一直按比例降低，这个过程体现了产品可无限次再制造特征。

假设约束（21）对应的Lagrange乘子分别为k，且=[k]K×1。所有需求市场最优行为可描述为变分不等式，即确定（Q3*，Q5*，ρ*，*）∈ΩK，满足：

∑Nn=1∑Kk=1[ρ*nk+cK*nk-rk*k-ρ*k]×[qnk-q*nk]+∑Ii=1∑Kk=1[αuk（Q5*）+*k-ρu*ki]×[quki-qu*ki]+

∑Kk=1[∑Nn=1q*nk-dk（ρ*;θ，β）]×[ρk-ρ*k]+

∑Kk=1[rk∑Nn=1q*nk-∑Ii=1qu*ki]×[k-*k]≥0（22）

（Q3，Q5，ρ，）∈ΩK，其中ΩK=RNK+KI+K+K+。

从式（22）的第2项可知，当qu*ki>0时，有αuk（Q5*）+*k=ρu*ki，由αuk（Q5*）为单调递增函数，因此，当Q5*增加，则ρu*ki增加，即回收商支付给消费者补偿负效用的回收价格越高，这一分析与实际中的情况相一致。

3.5回收商层的最优行为及均衡条件

市场内的废旧品由回收商提供一回收价格，回收后销售给制造商。该再制造过程可降低产品使用后产生的废弃物对环境的影响。由前述符号，各回收商的利润最大化目标可表示为：

max πi=∑Mm=1ρuimquim-∑Kk=1ρukiquki-∑Kk=1cuki（quki）-∑Mm=1cuim（quim）（23）

s.t.∑Mm=1quim≤∑Kk=1quki（24）

假设约束（24）对应的Lagrange乘子为γi，则γ=[γi]I×1。回收商间进行非合作Nash博弈，其最优行为可描述为变分不等式，即确定（Q4*，Q5*，γ*）∈ΩI，满足：

∑Ii=1∑Mm=1[cuimquim+γ*i-ρu*im]×[quim-qu*im]+∑Ii=1∑Kk=1[ρu*ki+

cukiquki-γ*i]×[quki-qu*ki]+∑II=1[∑Kk=1qu*ki-∑Mm=1qu*im]×

[γi-γ*i]≥0（25）

（Q4，Q5，γ）∈ΩI，其中ΩI=RIM+KI+I+。

从式（25）的第1项可以得到，ρu*im=cuimquim+γ*i;从式（25）的第2项可以得到，当qu*ki>0时，γ*i=cukiquki+ρu*ki，可见当ρu*ki增加时，ρu*im也增加。根据前文对制造商的分析，ρu*im对下游交易价格也产生影响。因此，闭环供应链网络是一个复杂的系统，其内部的因素之间存在一定程度的相互影响，尤其是各层的交易价格之间存在着传递关系，并按其中的某一价格增加，其他层间的交易价格也会产生变化。

3.6闭环供应链网络均衡模型

前文结合供应商层、制造商层、零售商层、需求市场层和回收商层的有关目标，分别获得了各层的Nash博弈均衡条件，分别由式（5）、式（12）、式（17）和式（25）所给出。而当各层决策者均处于Nash均衡状态时，整个闭环供应链网络即达到Nash均衡状态。因此，通过将式（5）、式（12）、式（17）和式（25）求和，即可獲得整个闭环供应链网络的Nash均衡条件，可用式（26）表示。其中层间交易价格为内生变量，求和过程中抵消。故基于环境保护目标和消费者低碳环保意识的闭环供应链网络的均衡条件为：

确定（q1*，q2*，qu*，Q1*，Q2*，Q3*，Q4*，Q5*，ρ*，μ*，η*1，η*2，η*3，δ*，*，γ*）∈Ω，满足：

∑Mm=1[fSs（q1）qrs-μ*s+α1tcβ1s]×[qrs-qr*s]+∑Mm=1[fMmqrm+fm（qr*）qrm-βrη*1m+η*3m+α2tcβ3m]×[qrm-qr*m]+∑Mm=1[fumqum+cm（qu*m）qum-βuη*1m+η*2m]×[qum-qu*m]+∑Ss=1∑Mm=1[c*smqrsm+μ*s+α1tcβ2sm-η*3m]×[qrsm-qr*sm]+∑Mm=1∑Nn=1[c*mnqmn+η*1m+α2tcβ4mn+cn（Q2*）qmn-δ*n]×[qmn-q*mn]+∑Ii=1∑Mm=1[cu*imquim-η*2m+γ*i]×[quim-qu*im]+∑Nn=1∑Kk=1[c*nkqnk+cK*nk+δ*n+α3tcβ5nk-rk*k-ρ*k]×[qnk-q*nk]+∑Ii=1∑Kk=1[αuk（Q5*）+*k+cu*kiquki-γ*i]×[quki-qu*ki]+∑Kk=1[∑Nn=1q*nk-dk（ρ*;θ，β）]×[ρk-ρ*k]

+∑Ss=1[qr*s-∑Mm=1qr*sm]×[μs-μ*s]+∑Mm=1[βrqr*m+βuqu*m-∑Kk=1q*mn]×[η1m-η*1m]+∑Mm=1[∑Ii=1qu*im-qu*m]×[η2m-η*2m]+∑Mm=1[∑Ss=1qrsm-qrm]×[η3m-η*3m]+∑Nn=1[∑Mm=1q*mn-∑Kk=1q*nk]×[δn-δ*n]+∑Kk=1[rk∑Nn=1q*nk-∑Ii=1qu*ki]×[k-*k]+∑Ii=1[∑Kk=1qu*ki-∑Mm=1qu*im]×[γi-γ*i]≥0 （26）

（q1，q2，qu，Q1，Q2，Q3，Q4，Q5，ρ，μ，η1，η2，η3，δ，，γ）∈Ω，其中Ω=ΩS×ΩM×ΩN×ΩI。

本文研究的是非线性优化问题，其可行域为凸集，解决问题的关键步骤是将优化问题最优解满足的条件转化为有限维变分不等式形式，其特点是维度高，求解难，一般需选择特定算法求得数值解，本文拟选择修正投影收缩算法进行求解[30]。

4数值算例

考虑由2供应商、2制造商、2零售商、2需求市场和2回收商组成的闭环供应链网络，有关参数设定为：βr=1，βu=0.9，rk=0.3，a=300，β1s=2.5、2sm=1.5、β3m=2.5、β4mn=1.5、β5nk=1.5，θ=0.3，tc=1。

有关函数设定如下：

fs（q1）=2.5（qrs）2+qrsqr3-s+2qrs，csm=csm（qsm）=（qrsm）2+1，fm（qrm）=2（qrm）2+qrm+1，fMm=fMm（βr，qr）=2（βrqrm）2，+βrqrm+2，fum=fum（βu，qu）=1.5（βuqum）2+βuqum+2，cm（qum）=0.5（qum）2+1，cmn=cmn（qmn）=（qmn）2+3qmn+1，cuim=cuim（quim）=0.5（quim）2+quim+1，cn=cn（Q2）=（∑2m=1qmn）2，cnk=cnk（qnk）=0.5（qnk）2+qnk+2，cnk=cnk（qnk）+0.5，cuki=cuki（quki）=0.1（quki）2+quki+1，αuk（Q5）=0.5（∑2i=1∑2k=1quki）+5。

另外，dk（ρ;θ，β）=a-ε1ρk-ε2∑i≠kρi-ε3θ∑Ss=1β1s+∑Ss=1∑Mm=1β2sm+∑Mm=1β3m+∑Mm=1∑Nn=1β4mn+∑Nn=1∑Kk=1β5nk-β0，其中ε1=1.3，ε2=0.8，ε3=0.4，行業标准β0=20。

算例中包含Lagrange乘子在内共有42个变量，用Matlab软件编制程序，迭代步长固定为0.01，初始误差取2，终止误差取10-8，初值选择元素为1的列向量。

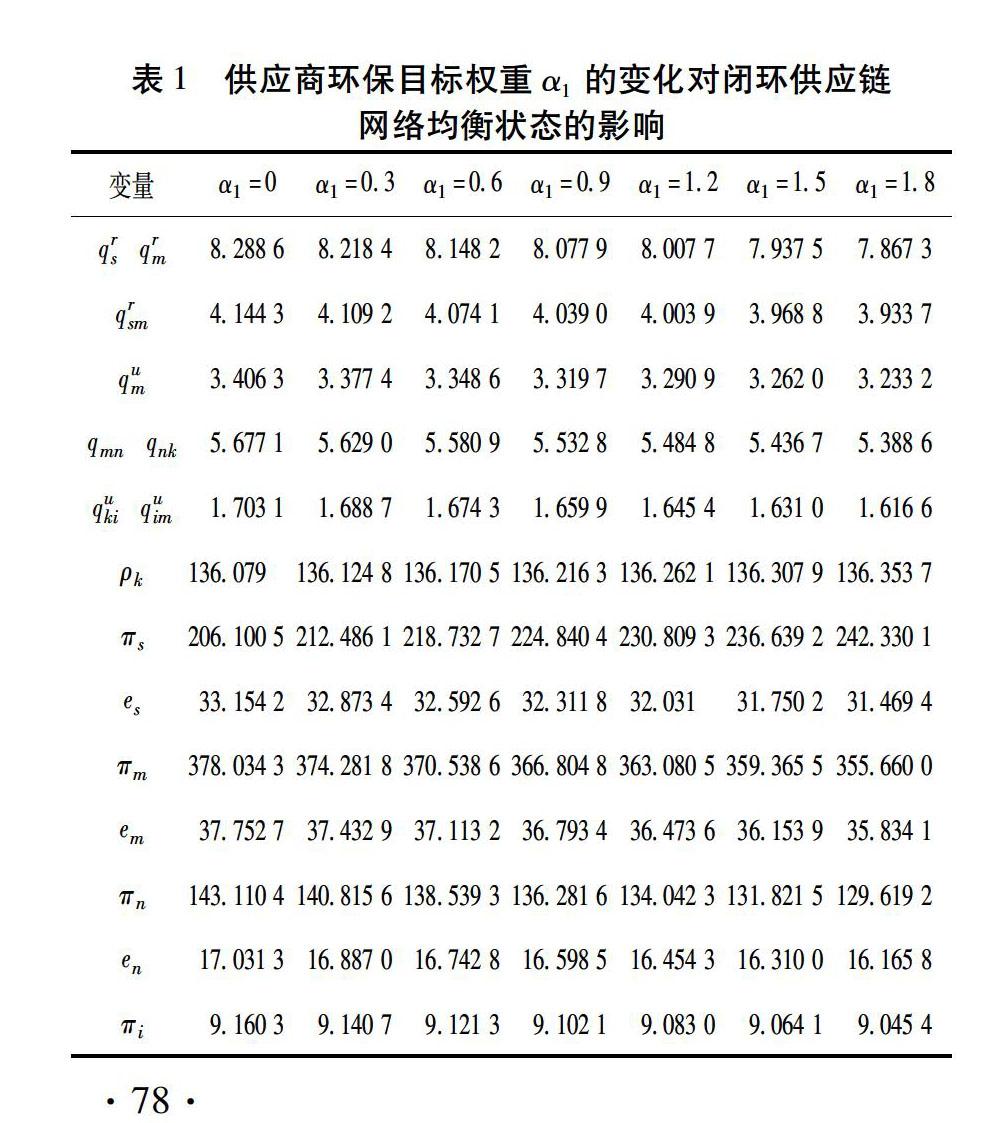
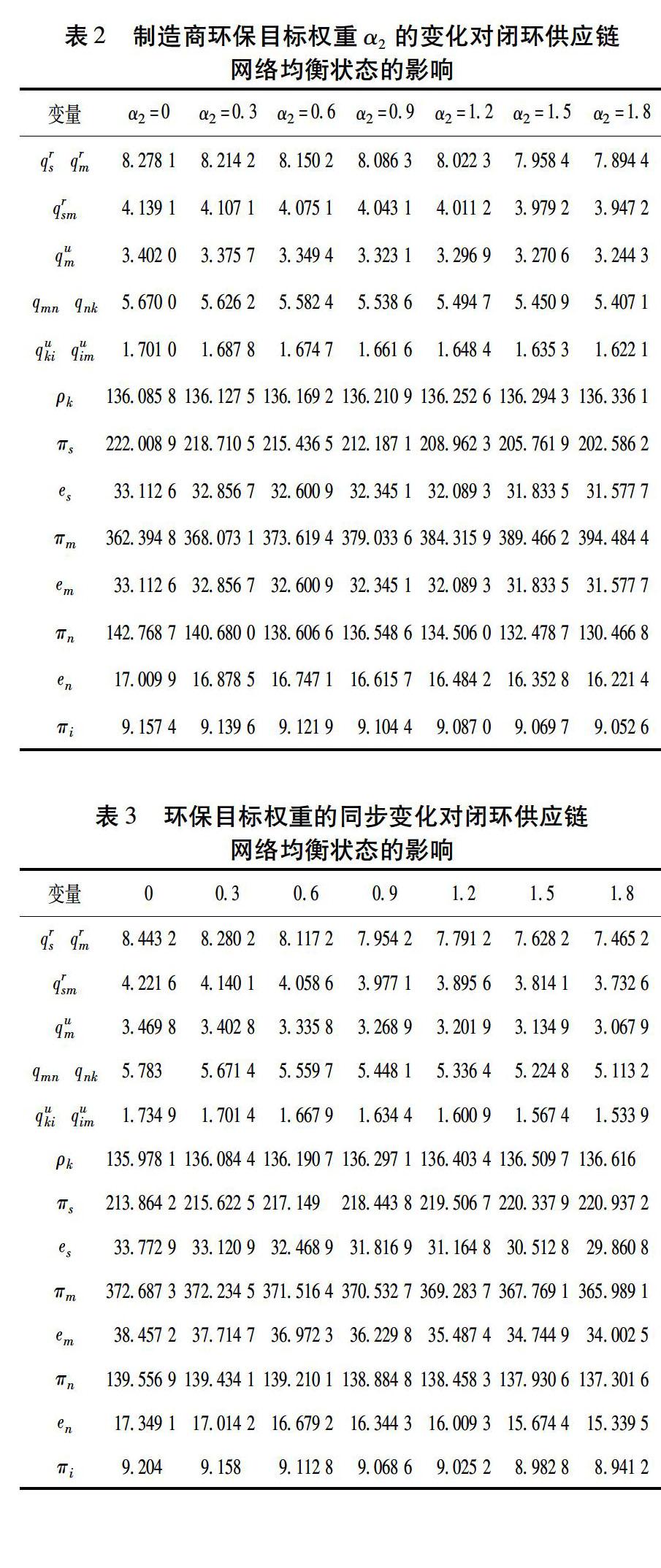
模型中涉及的参数较多，主要针对各层网络成员的环境目标权重系数α1、α2、α3和消费者低碳环保因子θ进行分析：①其余权重均为1时，α1、α2分别按照0∶0.3∶1.8增加，得到两组均衡解，结果列于表1至表2中;②权重系数α1、α2和α3同时按照0∶0.3∶1.8增加，所得均衡结果列于表3中;③消费者低碳环保因子按照0∶0.1∶1增加，主要决策变量和碳排放量结果用图2至图6表示。

各权重系数的大小表明了环境保护目标相对于经济利润目标的相对重要程度，权重系数为0则表明该企业成员仅关注经济目标而不关注环境目标，权重系数的不断增加，则表示企业对环境保护目标的重视程度逐渐增加。

从表1中可以看出，随着供应商环保目标权重α1的增加，原材料生产量和交易量、产品生产量和交易量均不断减少，也引起废旧品回收量的减少，需求市场的价格则出现小幅的增加。同时，由于交易量的减少，制造商、零售商和回收商的利润随之降低;供应商利润呈现增加趋势，原因是供应商与制造商间的价格上涨较为明显，带来的利润增加超过了由于交易量下降引起的利润下降，这说明供应商对环境保护目标的重视程度增加与其利润目标实现在一定程度上保持一致。

碳排放量方面，在环保目标权重系数增加过程中，所有企业的碳排放量以及总的碳排放量一直减少，则对环境的负外部效用也逐渐减小，说明企业环保意识的增加对环境保护能起到引导作用。

观察表2，各生产量和交易量的趋势与表1一致，各变量的最优解均随制造商环保目标权重α1增加而降低，需求市场中消费者支付的价格呈增加趋势。企业利润方面，供应商、零售商和回收商的利润均呈现缓慢减少趋势，而制造商利润出现较为明显的增加趋势，其原因同样是制造商与零售商间产品交易价格的上涨引起的利润增加，超过了由于交易量下降引起的利润减少，这也说明当制造商重视环境保护方面时，其环境保护目标和经济目标一定程度上也存在一致性。同时，所有企业的碳排放量和总碳排放量均随制造商环保目标权重的增加而减小，表明不仅制造商自身的经济目标和环境保护目标一致，整个闭环供应链的经济目标和环境保护目标也一致。

结合前述分析可预知，零售商的环保目标权重增加时，生产量和交易量也会减少，供应商、制造商和回收商利润减少，而零售商利润增加，各类企业碳排放量减少，限于篇幅，不再赘述。

接下来分析表3。当供应商、制造商和零售商的环保目标权重同步增加时，各决策变量和企业利润出现了与其分别增加时不同的变化趋势。权重系数的同步增加，显然对闭环供应链网络中各决策变量产生了显著影响，此时生产量与交易量以较快的速度减少，所有企业的碳排放量也明显降低。各企业利润的变化程度比各环保权重系数分别变化时平缓，具体表现为供应商利润缓慢增加，制造商、零售商和回收商的利润缓慢减小。这说明当闭环供应链网络中的某一类企业对环境保护的重视程度增加，而其他成员对环保目标的重视程度较低或维持不变时，则该类企业自身的利润和环境保护目标可以同时得到改善;但当闭环供应链网络中所有企业对环境保护目标的重视程度按相同的速度增加时，则不能保证所有企业均受益，且对利润的影响在很大程度上相互抵消。

对比表1、表2和表3可知：尽管环保目标权重同步增加时各企业利润的变化较为缓慢，但是也存在某种情况比其他情况更优的参数取值范围。如在表1中，当α1>1.5后继续增加时，其制造商利润将一直比表3中低。而表2中的α2>1.2时，制造商的利润比表3的任何情况下更高。供应商利润也可做类似分析。这说明闭环供应链网络的整体利益与各企业的自身利益存在较大的分歧，且协调起来较为困难。当各类企业均重视环境保护目标后，环境目标能够实现，其利润目标却存在不确定性。

以下对消费者的低碳环保意识进行分析。从图2至图5可以看出，在单位产品碳排放量给定的前提下，随着消费者低碳环保因子的增强，各生产量均呈现减少的趋

勢;同样，需求市场产品价格的降低幅度较大，表明此时消费者不愿支付较高的价格来购买产品。鉴于交易量与交易价格的减少，各企业利润均出现不同程度的降低。这说明在单位产品碳排放量不变的条件下，提高消费者环保意识会对供应链中企业利润与低碳社会的形成构成一定压力。

图6中给出了各类企业碳排放数量和总碳排放数量随消费者低碳偏好的变化情况，且eh=es+em+en。该图显示，各类企业的碳排放量随消费者低碳偏好的增加而降低，这主要归因于生产量和交易量的降低。换言之，在单位碳排放量和环保目标权重不变、仅消费者低碳环保因子增加的情形下，碳排放量减少，环保绩效得到改善。进一步结合图2至图5可知：如果仅强调提高消费者低碳意识而不改善企业的生产和交易技术条件，将导致企业经济目标与环保目标的不一致现象，因此，企业经济目标和社会环境保护目标的同时实现是一个复杂的工程，实际中可以考虑和其他措施一起来解决该现象。

5结论

本文针对由原材料供应商层、制造商层、零售商层、回收商层和需求市场层组成的闭环供应链网络，考虑现实中消费者的低碳环保意识，分别给出了各类企业成员利润最大化与碳排放量最小化双重目标下的优化问题，然后借助权重系数将其转化为单目标规划问题进行处理，运用变分不等式方法分别获得了各层的Nash竞争均衡条件，重点对网络中存在交易行为时交易价格的相关性质进行分析，在此基础上构建了整个闭环供应链网络均衡模型。运用修正投影收缩算法设计了模型最优解的Matlab计算程序。算例中结合不同权重系数和消费者低碳环保因子的变化进行了分析，获得了一定的管理学启示。结果表明：某一类成员环保目标权重系数的增加对其自身提高经济利润与环境绩效均有利;而环保目标权重系数的同步增加则对不同类型企业产生不同的影响。尽管消费者低碳环保因子的增加能够改善环境绩效，但却也使各网络成员与闭环供应链网络的整体收益下降。

本研究尚存在一些不足，如仅考虑了单周期静态模型，未来可将其拓展至多周期环境下，考察企业当期采用碳减排技术对未来决策与利润的影响。此外，通过将政府给定的碳减排目标与奖惩机制引入，建立StackelbergNash均衡模型来刻画政府与闭环供应链网络成员的交互行为也是重要的研究方向之一。

（编辑：王爱萍）

参考文献

[1]DU S F， HU L， SONG M. Production optimization considering environmental preference and preference in the Capandtrade System [J]. Journal of cleaner production， 2016， 112（20）：1600-1607.

[2]GUIDE JR V D R， VAN WASSENHOVE L N. The evolution of closedloop supply chain research [J]. Operations research， 2009， 57（1）： 10-18.

[3]GOVINDAN K， SOLEIMANI H， KANNAN D. Reverse logistics and closedloop supply chain： a comprehensive review to explore the future [J]. European journal of operational research， 2015， 240（3）： 603-626.

[4]SOUZA G C. Closedloop supply chains： a critical review， and future research [J]. Decision sciences， 2013， 44（1）： 7-38.

[5]GOVINDAN K， SOLEIMANI H. A review of reverse logistics and closedloop supply chains： a journal of cleaner production focus [J]. Journal of cleaner production， 2017， 142： 371-384.

[6]CHANG X， XIA H， ZHU H， et al. Production decisions in a hybrid manufacturingremanufacturing system with carbon cap and trade mechanism [J]. International journal of production economics， 2015， 162： 160-173.

[7]YENIPAZARLI A. Managing new and remanufactured products to mitigate environmental damage under emissions regulation [J]. European journal of operational research， 2016， 249（1）： 117-130.

[8]HE R， XIONG Y， LIN Z. Carbon emissions in a dual channel closed loop supply chain： the impact of consumer free riding behavior [J]. Journal of cleaner production， 2016， 134： 384-394.

[9]BAZAN E， JABER M Y， ZANONI S. Carbon emissions and energy effects on a twolevel manufacturerretailer closedloop supply chain model with remanufacturing subject to different coordination mechanisms [J]. International journal of production economics， 2017， 183：394-408.

[10]聂佳佳， 王拓， 赵映雪，等. 碳排放约束下再制造闭环供应链回收策略[J]. 管理工程学报， 2015 （3）： 249-256.

[11]李辉， 汪传旭， 徐朗，等. 闭环供应链碳减排和低碳宣传决策与协调[J]. 计算机集成制造系统， 2018， 24（5）： 1279-1291.

[12]李进， 朱道立. 模糊环境下低碳闭环供应链网络设计多目标规划模型与算法[J]. 计算机集成制造系统， 2018， 24（2）： 494-504.

[13]邢光军， 李培君. 碳减排情形下的闭环供应链差别定价模型研究[J]. 软科学， 2017， 31（9）： 138-144.

[14]王道平， 张博卿， 王路. 考虑随机回收量的闭环供应链碳减排与定价策略研究[J]. 软科学， 2017， 31（8）： 86-90.

[15]张杰芳， 曹细玉. 碳限额政策下闭环供应链的生产决策及协调研究[J].软科学，2018， 32（2）： 44-49.

[16]NAGURNEY A， DONG J， ZHANG D. A supply chain network equilibrium model [J]. Transportation research： part E， 2002， 38（5）：281-303.

[17]HAMMOND D， BEULLENS P. Closedloop supply chain network equilibrium under legislation [J]. European journal of operational research， 2007， 183（2）：895-908.

[18]YANG G F， WANG Z P， LI X Q. The optimization of the closedloop supply chain network [J].Transportation research： Part E， 2009， 45（1）：16-28.

[19]QIANG Q， KE K， ANDERSON T， et al. The closedloop supply chain network with competition， distribution channel investment， and uncertainties [J]. Omega， 2013， 41（2）：186-194.

[20]張桂涛， 胡劲松， 王磊，等. 考虑消费者渠道偏好的多期闭环供应链网络均衡[J]. 系统工程理论与实践， 2016， 36（2）： 347-362.

[21]NAGURNEY A， TOYASAKI F. Supply chain supernetworks and environmental criteria [J]. Transportation research： part D， 2003， 8（3）：185-213.

[22]马秋卓， 宋海清， 陈功玉. 考虑碳交易的供应链环境下产品定价与产量决策研究[J]. 中国管理科学， 2014， 22（8）： 37-46.

[23]ZHANG G T， ZHONG Y G， SUN H， et al. Multiperiod closedloop supply chain network equilibrium with carbon emission constraints [J]. Resources， conservation and recycling， 2015， 104： 354-365.

[24]杨玉香， 张宝友， 孟丽君，等. 基于环境责任的闭环供应链网络多准则决策均衡问题[J]. 系统管理学报， 2014， 23（1）： 13-20.

[25]熊中楷， 张盼， 郭年. 供应链中碳税和消费者低碳意识对碳排放影响[J]. 系统工程理论与实践， 2014， 34（9）：2245-2252.

[26]WANG Q，ZHAO D，HE L. Contracting emission reduction for supply chains considering market lowcarbon preference[J]. Journal of cleaner production， 2016， 120：72-84.

[27]JI J N， ZHANG Z Y， YANG L. Carbon emission reduction decisions in the retail/dualchannel supply chain with consumer preference[J]. Journal of cleaner production， 2017， 141：852-867.

[28]吕宝龙，张桂涛，刘阳，等. 考虑碳税和产品绿色度的闭环供应链网络Nash博弈均衡模型[J].中国人口·资源与环境， 2019， 29（1）： 59-69.

[29]王文宾， 邓雯雯， 白拓， 等. 碳排放约束下制造商竞争的逆向供应链政府奖惩机制研究[J].管理工程学报， 2016， 30（2）：188-194.

[30]HE B S， XU Y， YUAN X M. A logarithmicquadratic proximal predictioncorrection method for structured monotone variational inequalities [J]. Computational optimization and applications， 2006， 35（1）：19-46.