基于鲍摩配送中心选址的研究
——瓦尔夫模型对印方向物资
2019-12-30王超群
□ 王超群
(陆军军事交通学院 学员五大队研究生队,天津 300161)
1 研究目的及意义
习主席曾在军委后勤工作会议中指出要努力建设强大的现代化后勤,建设一切为了打仗的后勤。未来大规模作战对后勤物资保障提出了更高的要求,在对前线输送紧急物资时,需要物资配送中心进行统一的调配,因此,物资配送中心的选址至关重要。合理的选址能够节约战时宝贵的经费,省去大量的维护成本和物资运输成本。
选址问题一直是军事物流系统规划中研究比较广泛的内容,但相关方面的研究目前比较少见,选址问题涵盖了很多要素,并且各要素相互制约,因此,得出一个合理的解决方案并不简单,前面也有学者利用重心法、层次分析法建立模型,也引用遗传算法求解以得到最优方案。战争阶段我们考虑最多的就是军事经济性的因素,本文以经济性为目标建立模型,同时保证物资能够准确及时运往目的地,选用鲍摩——瓦尔夫模型进行分析,加以实例给出一个合理的选址方案。
2 鲍摩——瓦尔夫模型的建立
鲍摩——瓦尔夫模型又称为多节点单品种选址模型,如图1所示。其考虑了运输成本,而且还考虑了可变成本和固定成本,因此将鲍摩-瓦尔夫模型用于解决考虑运输费用和存储中心经济规模费用的物资配送中心选址问题,可为物资配送中心选址问题提供一种方便有效的计算方法。
假设模型中有m个资源点为前线接收点(需求点)提供单一品种物资(例如某药品),物资经由从候选点集合中选出的军事物流节点即物资配送中心运送给n个前线接收点也或者采取直接送达的方式。需要解决的问题是如何从s个候选点中选择若干个军事物流节点作为物资配送中心,使得已知的后方基地(资源点)通过物资配送中心运送单一品种物资至前线各接收点所需要的物流成本最小,模型中也存在从后方基地直接运送到接收点的情况。
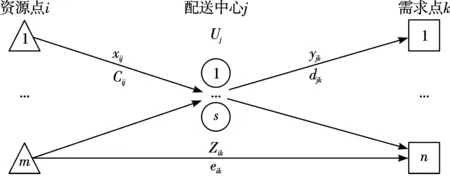
图1 鲍摩——瓦尔夫模型示意图
建立目标函数:
其中:
xij:备选配送中心j从资源点i进货的物资数量;
cij:备选配送中心j从资源点i进货的单位物资进货费用;
yjk:从备选配送中心j向需求点k进行配送的物资数量;
djk:从备选配送中心j向需求点k进行配送的单位物资配送费用;
zik:从资源点i向需求点k进行直达配送的物资数量;
eik:从资源点i向需求点k进行直达配送的单位物资配送费用;
vj:备选配送中心j被选中后基建投资费用(固定费用,与流量规模无关);
wj:备选配送中心j的单位物资存储费用率(变动费用,与流量规模有关)。
鲍摩——瓦尔夫模型的目标函数要求配送中心选址规划方案的总成本最小。并要满足如下五个约束条件:
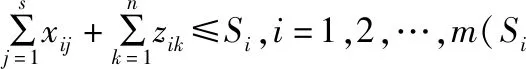
第一约束条件保证资源点运出的物资总量不大于资源点的生产或供货能力;
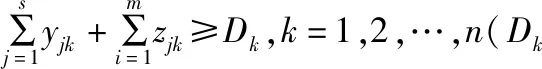
第二约束条件有效地保证所有需求点都会得到完全满足而不会出现缺货情况;
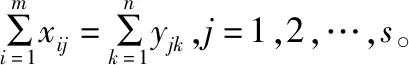
第三约束条件要求每个配送中心运进的物资总量等于运出的物资总量;
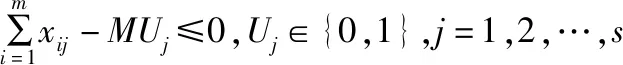
第四约束条件保证被选中的配送中心候选点(Uj=1)才有物资的周转量而被淘汰的配送中心候选点(Uj=0)无物资周转量;
⑤xij、yjk、zik≥0。
第五约束条件规定所有的物资流量均不能小于零。
通过大量的数据拟合,物流设施存储费用与流量规模(吞吐量)之间数量关系的数学表达式为:
Hj=物流设施j的存储费用;
Gj=物流设施j的吞吐量;
μj、p=函数常系数。
设物流设施在某一规模时的边际成本为wj,则:
当p=0.5时,物流设施j的存储费用Hj和边际成本wj为:
因此,如果已经确定了物流设施的规模,那么在此规模下的存储费率就可以由上述的边际成本wj的公式计算得到。
3 启发式算法
存储费用可以看做是非线性函数,那么模型就是非线性模型,其求解计算过程非常复杂,所以采用启发式算法,能够较好地解决物流设施存储费用的非线性的问题。
第一步,求初始解。首先,令各备选配送中心的规模均为0,即Gj=0;然后,对资源点经由配送中心再到需求点之间物资流通的所有组合求单位运输成本最小值,即寻找运输成本最低的线路,其运输成本为:
再引入变量Gik,表示从资源点i经由备选配送中心j再到需求点k的物资流通量,解下列线性规划的方程求Gik:
第二步,求二次解。首先,设经由备选配送中心j的所有组合的集合为Gj,则备选配送中心j的吞吐量为:
然后,以运输费率和存储费率之和最小为目标,求最省路线:
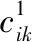
第三步,求最优解。按照步骤二反复计算,直至Gj不变,即获得满意解。
4 实例分析
假设未来中印边境发生大规模战争,急需从后方运送某种药品,运送方式主要为航空运输和物资配送中心分配,物资从后方军事物流基地发送到前方机场。起点Ai共有2个,依次是武汉天河国际机场和郑州新郑国际机场。终点Bi共有10个,依次是拉萨贡嘎国际机场、阿里昆莎机场、昌都邦达机场、日喀则和平机场、林芝米林机场以及未来投入使用的那曲、普兰、定日、隆子、亚东各县的前沿机场。现代表候选的物资配送中心Di共有5个,依次是西宁曹家堡国际机场、玉树巴塘机场、成都双流国际机场、阿坝红原机场和甘孜康定机场。选择哪几个机场作为配送中心以及怎样的配送方案使得成本最小是需要解决的问题。已知各军事物流基地到配送中心候选点的单位运输成本和候选点到需求点的平均单位配送成本及基地供应量和需求点需求量,如表1和表2所示。表中成本数据由各点间相对距离确定,供应量和需求量根据各点战略地位和规模大小等因素决定。

表1 军事物流基地到配送中心候选点的单位运输成本及供应量

表2 配送中心候选点到需求点的平均单位配送成本及需求量
已知配送中心候选点存储费用函数表如表3所示,μj由机场地理条件和规模大小决定。

表3 配送中心候选点存储费用函数表
4.1 求初始解
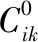
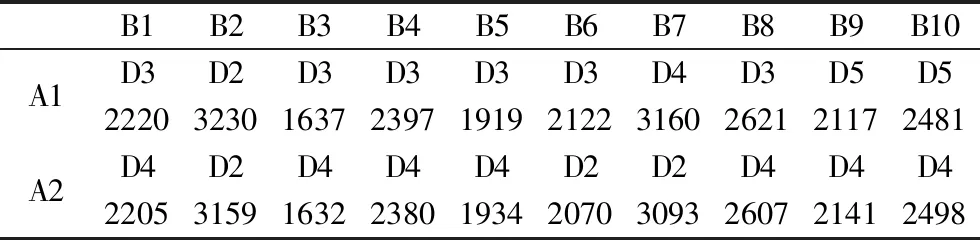
表4 从资源点到需求点的最小运输成本及经由的配送中心候选点
根据表4中的运输成本“按需就近”分派物资供应量并得到配送中心选址规划的初始解,如表5所示。

表5 配送中心选址规划的初始解
4.2 求二次解
利用初始解和各配送中心的存储费用,可以汇总出候选点的吞吐量和存储费率,计算结果如表6所示。

表6 初始解下的各配送中心候选点吞吐量和存储费率
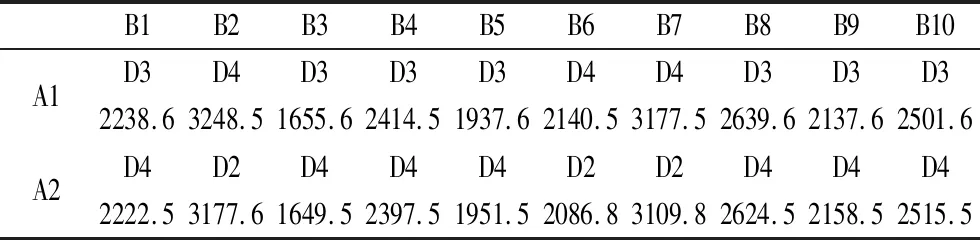
表7 从资源点到需求点的最小运输成本及经由的配送中心候选点

表8 配送中心选址规划的二次解
4.3 求最终解
继续迭代,比较第四次解和第五次解,发现各配送中心候选点的吞吐量没有发生变化,无需再进行求解计算,故第五次解为最终解。最终解如表9所示。
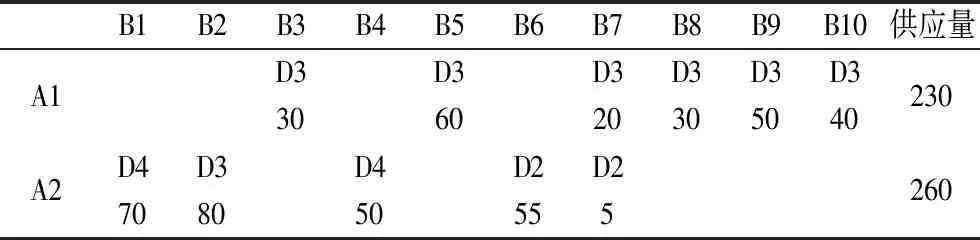
表9 配送中心选址规划的最终解
最终解是在候选的5个配送中心中选出3个作为物资配送中心,分别是D2、D3和D4。即玉树、成都和阿坝。其配送方案如图2所示。
5 结语
假设在未来大规模作战中,为解决配送中心选址和运输实施具体方案的问题,本文引用鲍摩——瓦尔夫模型,在满足最经济等条件下,解出最终解,为实际问题提供了一种合理的解决办法,进一步验证了该方法的可行性和科学性。
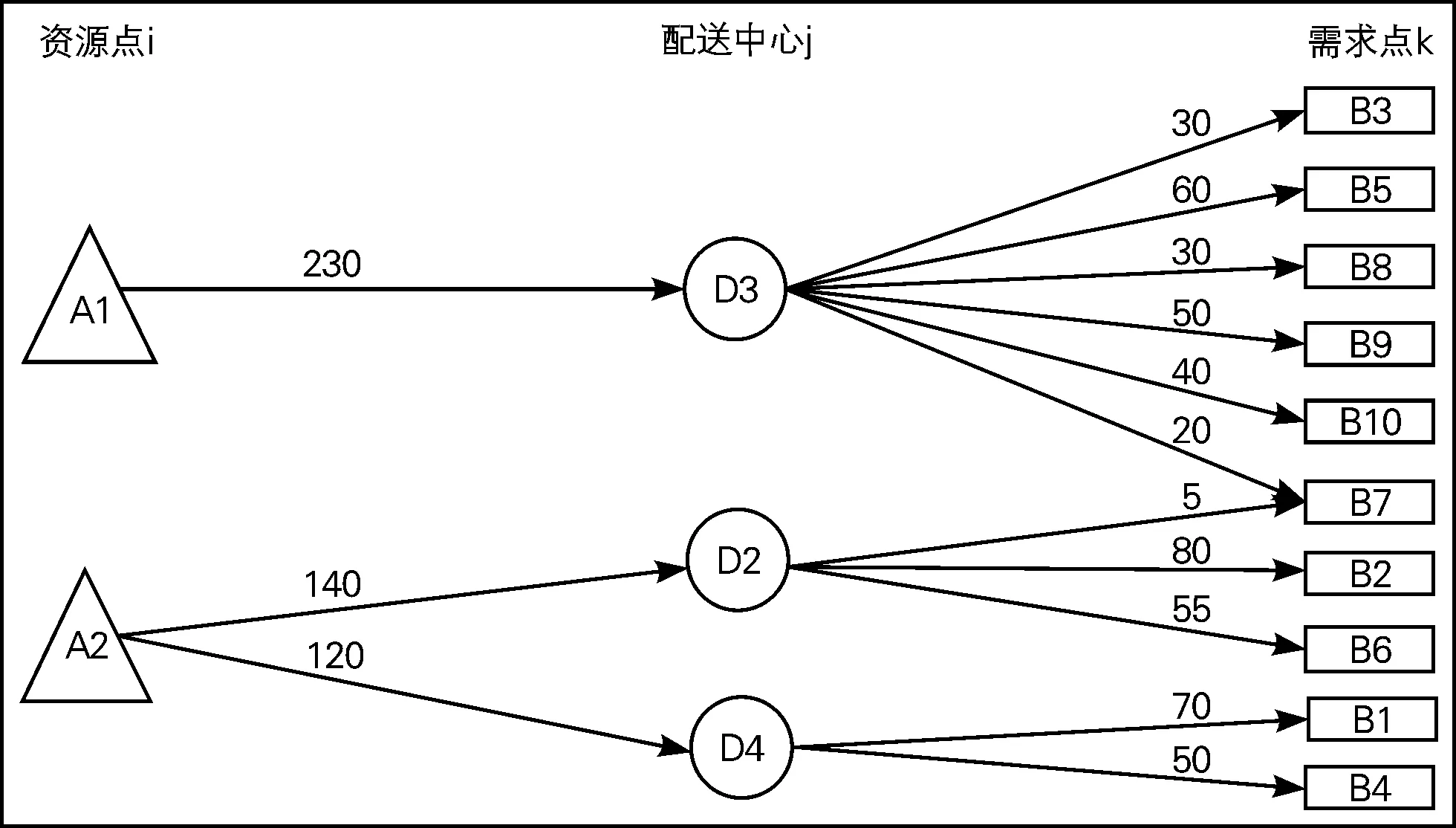
图2 鲍摩——瓦尔夫选址规划分配方案示意图
