低轨卫星TDMA通信中系统定时的研究

朱晋飞　程剑

摘要：在低轨卫星通信系统中，低轨卫星的高速运动给时分多址接入中的系统定时带来了较大的影响。为了提高系统定时精度和系统效率，分析了低轨卫星运动的特点和系统定时原理，提出基于低轨卫星运动模型辅助的开环系统定时跟踪方法，并进行了仿真。仿真结果表明，该方法能够对低轨卫星的运动和终端的系统定时进行较好的跟踪，克服了低轨卫星高速运动带来的影响。

关键词：低轨卫星;时分多址;系统定时

doi：10.3969/j.issn.1006-1010.2019.11.014        中图分类号：TN929.5

文献标志码：A        文章编号：1006-1010（2019）11-0088-06

引用格式：朱晋飞，程剑. 低轨卫星TDMA通信中系统定时的研究[J]. 移动通信， 2019，43（11）： 88-93.

Research on the System Timing of TDMA in Low-Orbit Satellites

ZHU Jinfei， CHENG Jian

（Army Engineering University of PLA， Nanjing 210000， China）

[Abstract] In the low-orbit satellite communication system， the high speed motion of low orbit satellite brings great influence on the system timing in time division multiple access （TDMA）. In order to improve the system timing precision and system efficiency， the characteristics of low-orbit satellite motion and the principle of system timing are analyzed. An open-loop system timing tracking method is proposed based on the motion model of low-orbit satellite. The simulation results show that the proposed method tracks the motion of low-orbit satellite and the system timing of the terminal， and overcomes the influence of high speed motion of low-orbit satellite.

[Key words]low-orbit satellite; TDMA; system timing

0   引言

相比于靜止轨道卫星通信系统，低轨卫星通信系统由于轨道高度低而具有延迟低、发射成本低、空间传播损耗少等优点，同时，通过建立低轨卫星星座也能实现全球覆盖，因此低轨卫星通信系统正在成为全球卫星通信研究的热点[1]。

TDMA（Time Division Multiple Acess，时分多址接入）方式因具有较高的功率和频段利用率而被较多卫星通信系统使用，然而在低轨卫星通信系统中，低轨卫星相对终端站的高速运动，给终端站TDMA多址接入中的同步带来了较大影响。为了各终端站发射的突发信号能有序地通过卫星转发器，其系统定时同步是一个必须解决的问题。在静止轨道卫星通信系统中，系统定时同步主要采取参考突发结合测距的方法完成初始捕获，以及通过主站闭环调整的方式完成同步跟踪[2-3]。此外，针对移动通信终端，文献[4]提出了基于终端运动模型结合卡尔曼滤波预测算法的开环系统定时同步跟踪方法，文献[5]提出了基于运动终端的系统定时同步补偿方法。如果将这些方法直接应用在低轨卫星通信上，将会带来较大的系统定时误差，影响系统的传输效率。以相对某终端最大瞬时径向速度为6 400 m/s的低轨卫星为例，其往返延迟变化率最大达到42.6μs/s，如果每5 s闭环调整一次，那么运动造成的最大系统定时误差约为213μs，为了避免突发误入其他时隙造成干扰，这需要相对较大的保护时间。虽然通过缩短信令调整间隔可以减少系统定时误差，但相应也会增加系统网络信令开销，同样会降低系统的效率。

目前，在低轨卫星通信系统中，著名的铱星系统是采用较大突发保护时隙来克服低轨卫星高速运动的影响[6]，但是这降低了系统效率，因此对于低轨卫星TDMA多址接入的系统定时同步研究非常重要。针对该问题，本文将分析低轨卫星的运动特点以及TDMA接入过程和系统定时同步原理，提出基于低轨卫星运动模型辅助的系统定时同步跟踪方法。

1   低轨卫星运动的特点

在卫星运行的二体模型下，大部分低轨卫星以椭圆轨道运行，地面终端站观测到的卫星距离随时间是在不断变化中的，不同位置的终端站所观测的卫星距离也是不同的。根据卫星轨道参数和终端站的最大仰角，可以求得任意时刻卫星到终端站的距离为[7]：

（1）

其中，a是轨道椭圆半长轴，Re是地球平均半径，e是卫星轨道椭圆偏心率，f（t）是卫星t时刻卫星的真近点角，ωe是地球自转角速度，i是轨道椭圆倾角，t0是参考时刻，r（t）是卫星到地心的距离，其值为：

（2）

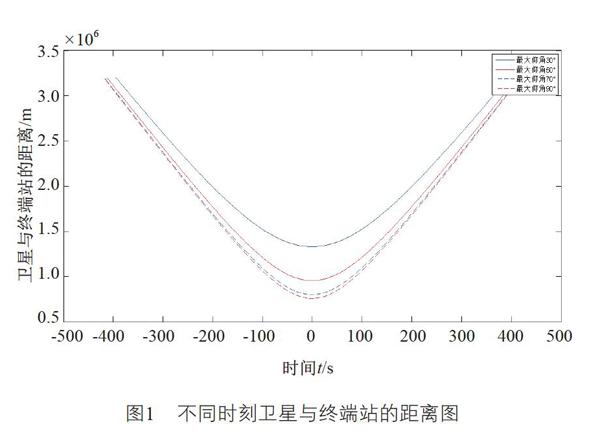
以铱星系统为例，不同最大仰角的终端站与卫星距离随时间变化的曲线如图1所示，从图中不难看出，终端站最大仰角越大，其距离变化最快，与卫星最小距离最小。当卫星进入终端站可视区内时，其与卫星的距离都是先变小后变大，在最大仰角时刻取得最小值。

2  终端TDMA接入过程和系统定时同步

原理

在低轨卫星通信系统中，终端站TDMA多址接入过程中主要完成系统定时同步和收发频率同步，系统定时同步是终端站将本站突发正确发射到卫星上指定时隙位置的过程，收发频率同步是终端站按照指定频率进行接收和发射信号的过程。

2.1  TDMA多址接入过程中的系统定时同步

卫星通信系统TDMA多址接入可分为五个基本过程，分别是初始化同步、登录过程、粗同步过程、细同步过程和同步维持过程[8]。如图2所示，在初始化同步过程中，终端站从前向链路信令信道中接收卫星广播的网络结构信息，主要包括超帧结构表（SCT， Superframe Composition Table）、帧结构表（FCT， Frame Composition Table）、时隙结构表（TCT， Time slot Composition Table）以及卫星位置表（SPT， Satellite Position Table）等信息。在登录过程中，终端站通过反向链路发射相应的接入突发请求到主站，主站收到接入请求后，验证身份，检测系统定时误差，而后通过前向链路信令信道反馈给终端。在粗同步过程和细同步过程中，终端站根据主站反馈的系统定时误差校正本站系统定时误差。在同步维持过程中，终端站根据主站不断反饋的系统定时误差修正本站的系统定时。

2.2  系统定时同步原理

如图3所示，参考站通过卫星定期转发参考突发到所有终端站，终端站接收到参考突发后，根据本站到卫星的双向延迟得到发射帧定时信息，再按照帧计划发射本站突发信息，从而确保本站发射的突发信号刚好位于卫星转发器上指定的时隙位置，避免与其他终端站发射的突发信息发生碰撞[9]。

从图中可以得接收参考突发时刻为：

SOFR（k）=SOFR（0）+kT+（S0（k）-S0（0））/c+Δtywie       （3）

终端站的发射延迟为：

Tn=dn+mT-RTT        （4）

其中，SOFR（0）和S0（0）分别是某次精确定时后的参考突发接收时刻和卫星到终端站的瞬时传播距离，SOFR（k）和S0（k）分别是终端站接收第k个参考突发的接收时刻和卫星到终端站的瞬时传播距离，Δt是kT时间内终端站相对卫星的钟差变化，c是光速，T是帧周期，m和dn是帧计划参数，RTT是终端站到卫星的往返时延。

在低轨卫星通信系统中，由于卫星的高速运动，终端站到卫星的往返延迟处于不断的变化之中，而且终端站在接收参考突发下行链路和发射突发上行链路的传播延迟也不一样。以相对某终端站最大瞬时径向速度6 400 m/s的低轨卫星为例，对于突发计划参数（m=0、dn=45 ms）的终端站，其接收参考突发的下行链路的传播延迟与发射突发的上行链路的传播延迟差约为960 ns，这同样也会对终端站系统定时造成较大误差。因此为了完成系统定时同步的精确跟踪，在跟踪往返延迟的变化时，前向下行链路和反向上行链路的传播延迟需要分开计算。

3   基于低轨卫星运动模型的终端系统定

时开环跟踪方法

当前，常见的目标运动模型有二阶匀速运动模型、三阶匀加速运动模型、Singer模型和当前统计模型（CA）等，其中Singer模型是将物体运动加速度建模成零均值自相关随机过程，当前统计模型是将加速度建模成非零均值自相关随机过程[10]。在目标跟踪系统中，不同场景的目标运动特点需选择不同的运动模型，只有当选择的运动模型与目标运动特点相吻合时才能很好地对目标进行跟踪。根据低轨卫星运动的特点，本文选择与其运动特点相吻合的当前统计运动模型。

从式（3）中可以看出，终端站接收参考突发的时刻反映了卫星与终端站距离的变化。另外，终端站相对卫星运动的径向速度与其参考突发的接收多普勒频移关系为νd=-cfd/fc，其中νd是径向速度，fd为终端站接收的多普勒频移，fc是终端站接收载波频率。因此终端站在获取精确的系统定时后，可以联合参考突发接收时刻和多普勒频移作为对终端站和卫星相对运动跟踪的观测量。

3.1  低轨卫星相对运动的当前统计模型

设当前统计模型的状态量为xk=（δk， νk， ak， bk， fb）T，其中δk=S0（k）-S0（0），νk表示接收第k帧参考突发时卫星与终端站的径向速度，ak表示接收第k帧参考突发时卫星与终端站的径向加速度，bk是径向速度的二阶变化率，fb表示终端站与卫星间的固定频偏。

那么当前统计模型的状态转移方程为：

xk=Axk-1+Bbk-1+Cqk-1            （5）

其中：

p1=[2-2αT+α2T2-2exp（-αT）]/2α3

p2=[-1+αT+exp（-aT）]/α2

p3=[1-exp（-aT）]/α

p4=exp（-αT）

参数中，α是卫星与终端的机动频率，一般取值为帧周期T的倒数。式（5）中qk-1是系统模型噪声，服从零均值高斯分布，其方差Q=2ασ2，其中σ2是速度二阶变化率扰动方差。

3.2  终端站接收参考突发的跟踪观测模型

在不考虑大气延迟变化的情况下，则终端站跟踪低轨卫星运动的观测方程为：

τk=Hxk+rk      （6）

其中，，rk是第k帧参考突发接收时刻和频率测量误差，服从零均值高斯分布，其方差设为R，Δfk是第k帧参考突发接收的频偏，由固定频偏和多普勒频移组成，τk是第k帧参考突发接收定时调整值，其值为：

τk=SOFR（k）-SOFR（0）-kT-Δt （7）

3.3  基于跟踪模型的卡尔曼滤波算法

由于建立的运动模型和观测模型都是线性的，因此可以采用均方根误差最小准则下最优的卡尔曼滤波算法进行估计和预测[11]。其估计预测步骤如下：

（1）根据当前估计状态预测下步状态：

Xk=AXk-1+Bbk-1 （8）

（2）計算预测误差协方差矩阵：

Pk|k-1=APk-1|k-1AT+Bσk-1BT+CQk-1CT      （9）

（3）预测观测量：τk|k-1=Hτk-1      （10）

（4）计算增益：Kk=Pk|k-1HT（HPk|k-1HT+Rk）-1   （11）

（5）更新估计：Xk=Xk|k-1+Kk（τk-τk|k-1）   （12）

更新协方差矩阵：Pk=Pk|k-1-KkHPk|k-1    （13）

终端站在获取到初始状态后，按照以上步骤迭代估计出每一帧起始时刻低轨卫星的相对终端的运动状态。

3.4  终端站系统定时跟踪计算方法

终端站通过闭环获取到精确地系统定时后，利用卡尔曼滤波算法，估计出接收第k帧时卫星到终端的下行链路传播距离变化量δk和卫星与终端站的瞬时径向速度νk，那么突发发送时终端站到卫星的上行链路的距离变化量可以估计为：

δku=δk+（νk-ν0）（mT+dn）    （14）

其中，ν0是最初定时调整后的卫星到终端站的瞬时径向速度。

这样终端站发送突发信号的发射定时调整值可以估计为：

ΔTk=（δk+δku）/c+Δt                      （15）

即：

ΔTk=（2δk+（vk-v0（mTf+dn））/c+Δt （16）

4   系统定时同步跟踪算法仿真及分析

4.1  仿真条件

目前低轨卫星通信系统比较多，采用TDMA多址接入的系统主要有美国的铱（Iridium）系统和美国与加拿大共同研制的ORBCOMM系统，因此本文选取铱（Iridium）系统和ORBCOMM系统中的三个不同卫星作为仿真场景。终端站地址选为北京，其坐标设为东经116°，北纬40°。选取某个可视时间范围下卫星轨道参数和终端最大仰角及最大仰角时刻卫星平近点角作为仿真条件，并且将最大仰角时刻设置为0时刻，其参数如表1所示。另外设置低轨卫星通信系统中终端站捕获参考突发的频率误差标准差为80 Hz[12]，接收时刻误差设置为1μ s和2μ s，帧周期为90 ms，终端站接收过程中的固定频偏为300 Hz。

4.2  仿真结果及分析

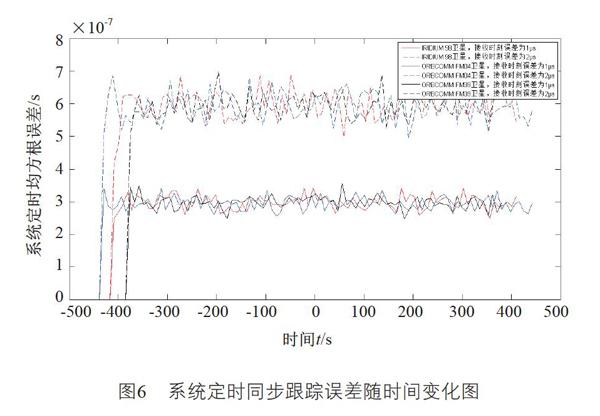
本文基于当前统计模型下低轨卫星位置的跟踪，分别对三个不同卫星条件下终端站时分多址接入过程中的距离和系统定时跟踪情况进行了仿真。图4给出了三个场景下卫星与终端站理论距离与估计距离随时间的变化仿真图，从图中可以看出对于不同的卫星轨道，采用本文估计方法估计的距离都能取得比较好的跟踪效果。图5给出了卫星与终端距离跟踪的均方根误差曲线，从图中可以看出初始捕获获得比较精确的距离后，再接着跟踪的过程中误差会增大，但是始终会维持在一个范围里，不会随着时间不断增加，这主要是系统模型误差与接收时刻误差相互影响的结果。图6给出了三个场景在不同参考突发接收时刻误差条件下，基于卫星位置跟踪的系统定时同步跟踪的误差仿真图，因为系统定时的精度主要由终端与卫星距离的精度决定，所以其仿真曲线与距离误差曲线类似，从图中可以看出在同一接收时刻误差情况下，跟踪过程中的系统定时误差在一个范围内波动，但比接收时刻误差小，而且也克服了低轨卫星高速运动带来的较大影响;同时接收时刻误差越小，其系统定时精度越高。因此基于当前统计模型的低轨卫星位置跟踪对于提高系统定时精度具有较好的效果，而且可以通过减少参考突发接收时刻误差来提高系统定时跟踪精度。

5   结束语

针对低轨卫星通信系统TDMA多址接入中的系统定时同步问题，本文研究了低轨卫星运动特点和终端接入过程中系统定时同步原理，采取当前统计模型和卡尔曼滤波算法来跟踪低轨卫星和终端间相对运动，最后利用跟踪结果实现系统定时同步的跟踪。仿真表明，该方法具有良好的跟踪效果，具有一定的工程实践意义，但在具体的硬件实现上还需要有进一步的研究。

参考文献：

[1] 李毅，侯睿，张更新. 发展我国低轨卫星通信星座系统的思考[J]. 国际太空， 2018（4）： 62-65.

[2] NUSPL P P， BROWN K E， STEENAART W， et al. Synchronization methods for tdma[J]. Proceedings of the IEEE， 1977，6（3）： 434-444.

[3] JOO I， KIM J H. Satellite TDMA controller design for timing acquisition and timing synchronization[C]//Vehicular Technology Conference. IEEE， 2004： 1934-1938.

[4] 罗飞腾，朱崇萱，兰瑞田. 适于机动TDMA卫通站的开环网络同步方法[J]. 无线电通信技术， 2013，39（3）： 20-23.

[5] 王秋婷，李云，张帅，等. 卫星移动通信系统的定时同步技术[J]. 无线通信技术， 2014，23（4）： 13-17.

[5] 吴果. 抗干扰卫星通信系统定时同步技术研究[D]. 西安： 西安电子科技大学， 2018.

[6] FOSSA C E， RAINES R A， GUNSCH G H， et al. An overview of the IRIDIUM （R） low Earth orbit （LEO） satellite system[C]//Aerospace & Electronics Conference. IEEE， 1998.

[7] 王爱华，王星原，陈丽婷. 低轨卫星多普勒频移特性几何估计算法[J]. 北京理工大学学报， 2016，36（12）： 1294-1297.

[8] 张松林，刘榕，王宏杰，等. DVB-RCS的终端同步流程分析[J]. 计算机技术与发展， 2011，21（8）： 200-203.

[9] KOGLER W， SCHLEMMER H， KOUDELKA O. Timing Synchronization in MF-TDMA Systems for Geostationary Satellites[Topics in Radio Communications][J]. Communications Magazine IEEE， 2007，45（12）： 36-42.

[10] 崔诵祺. 低轨卫星高动态通信链路同步技术研究[D]. 北京： 北京理工大学， 2015.

[11] STEVER M K. 统计信号处理基础[M]. 罗鹏飞，译. 北京： 电子工业出版社， 2011.

[12] 周文玉，张献民，郝学坤. TDMA卫星通信系统突发同步的性能研究[J]. 无线电通信技术， 2009，35（3）： 26-28. ★