融合多传感器数据的发动机剩余寿命预测方法

2019-12-27任子强司小胜胡昌华王玺

航空学报 2019年12期

任子强，司小胜，胡昌华，王玺

火箭军工程大学导弹工程学院，西安 710025

系统或设备在运行过程中，由于多种因素的影响，比如：外部环境、工作载荷、自身结构等，会出现不可避免的退化，甚至失效。对于大型结构件、复杂系统、军事武器、航空发动机等，系统无征兆的失效，将会带来经济、环境、人员方面的重大损失。为评估设备的健康状况，利用传感器数据对设备的状态进行监测，并对设备的剩余寿命(Remaining Useful Life, RUL)进行预测，这在状态维护中起着十分重要的作用。随着设备的退化，传感器数据(如温度、角度、压力和振动等)与设备潜在的退化过程有关。在给定失效阈值的情况下，可以通过传感器监测数据实现对设备的剩余寿命预测，这对减少设备故障造成的各类损失和提高系统的安全性与可靠性有着重要意义[1-2]。

近年来，航空航天技术发展迅速，作为其关键部件的航空发动机，对航空器的正常运转起着至关重要的作用。由于发动机系统结构复杂、工作环境恶劣多变，使得发动机安全性评估和维修替换策略制定等问题突出[3-4]。而航空发动机的RUL预测与健康管理(Prognostics and Health Management, PHM)技术的研究和应用，可以为其状态检修提供技术支持，有效确保飞行安全、降低重大风险事故的发生率、减少维修费用，提高航空器的可靠性，其中发动机的RUL预测是PHM中最具挑战的技术[5-6]。另外，在现有研究中，维纳过程具有良好的数学特性，既适用于描述单调系统的退化过程，也适合于描述非单调系统的退化过程，自Cox提出布朗运动的首达时间(First Hitting Time, FHT)分布函数[7]以来，此模型便在数据驱动的剩余寿命预测领域中得到广泛应用[8]。

关于设备的退化建模与RUL预测方面的研究已有众多文献成果，其中也包含了许多方法和技术[9]。对于设备退化建模与RUL预测，现有的文献大多集中在单个传感器信号在单个运行条件下的分析[10-11]。具体来说，通常首先根据历史监测数据建立随机退化模型，然后根据现场传感器实时采集到的监测数据对模型参数进行更新[11]，进而实现RUL预测。在这个过程中，当退化机制被充分了解，并且单传感器数据能够充分捕捉设备的退化特性，这类方法是有效的。然而，随着设备结构的日趋复杂，再加上运行环境的恶劣多变，依赖单一传感器信号通常不足以准确描述系统的潜在退化机制，从而导致RUL预测结果的不准确[12]。虽然可以使用多个传感器并单独分析相应的数据，但这往往会导致对RUL估计得过高或过低[13]。另外，国内外学者在多源传感器数据融合和剩余寿命预测方面也有一定的研究。赵广社等[5]通过发动机当前状态与健康状态之间的马氏距离构建了复合健康指标。Chehade等[7]研究了多故障模式下退化建模和预测分析的数据级融合方法；Yan等[14]研究了多传感器数据融合在退化建模与预测中的应用；Song等[15]研究了集成数据级融合模型和内核方法进行降级建模和预测分析的方法；Liu等[16-17]研究了集成数据融合方法以改进寿命预测的方法，以模型拟合误差、失效阈值方差最小为目标函数来确定融合系数；Fang等[18]研究了基于多传感器融合的单故障模式的寿命预测方法。

随着传感器技术的发展与进步，通常由多个传感器同时监测一个设备的健康状态。在多个传感器中，有的传感器监测数据与设备潜在退化机制相关，从而在设备退化过程中，退化趋势明显；而另外一部分传感器的监测数据与设备潜在退化机制相关程度不高，在设备的退化过程中，退化趋势不明显[13]。另一方面，即使某单一传感器监测数据与设备的潜在退化机制有很高的关联度，但也可能只是包含了退化设备的部分信息，并不能较为全面地反映出设备的退化机理。

因此，论文提出了一种数据融合方法，将多传感器数据进行线性组合，构造出一个复合健康指标(Composite Health Indicator，CHI)，用于表征发动机的复合退化量；通过真实寿命与预测寿命的预测均方误差最小确定出传感器融合系数；然后结合发动机历史寿命数据与实时监测数据，实现对发动机的RUL预测，最后选择商用模块化航空推进系统仿真(Commercial Modular Aero-Propulsion System Simulation, C-MAPSS)数据集进行数值仿真实验。

1 复合健康指标的构建

多传感器监测数据能够更加准确地表征发动机的退化特性，但是也给发动机模型的构建与多传感器数据的融合带来了挑战。论文提出了一种多传感器数据融合方法：将多传感器数据线性组合构建出一个CHI来表征系统的退化特性[14]，此方法可以解决数据处理和模型构建复杂的问题。

为完成CHI的构建，本节的主要内容为：① 线性构建复合退化量，同时确定复合退化量的失效阈值；② 为提高剩余寿命预测精度，对传感器数据进行归一化处理；③ 利用已经构建的CHI和已归一化后的数据对发动机进行退化建模，然后实现对发动机寿命的预测；④ 利用发动机的预测寿命与真实寿命确定CHI的融合系数，完成CHI的构建。

1.1 CHI的建模

令xi(t)表示第i(i=1,2,…,M)个训练发动机在t时刻融合多传感器数据的复合健康指标，其中M为训练发动机个数。因此，融合多传感器数据的复合健康指标{xi(t),t≥0}可以表示为

(1)

构建了复合健康指标xi(t)后，需先确定其失效阈值。当无法得知发动机的失效阈值时，一般将实际失效时刻对应的退化量作为失效阈值[14]。令xi(tNi)=xi,Ni为第i个训练发动机在失效时刻tNi的复合健康指标(N表示共有N组监测数据)，其值由式(1)在发动机失效时刻求得，也是复合失效阈值由单个失效阈值融合得到。

通常情况下，失效阈值是一个确定值，然而在实际应用中会发现，由于退化过程的随机性，不同训练发动机在真实失效时对应的退化量是不一样的。为了减小寿命预测的不确定性，在给定相同的失效模式和操作条件下，发动机的失效阈值通过使待定失效阈值与不同训练发动机失效时刻对应的退化量的方差最小来确定[13]。具体地，失效阈值可确定为

(2)

式中：P为发动机失效阈值。

由xi(tNi)的定义可以求得训练发动机的平均失效阈值为

(3)

1.2 多传感器数据的归一化

在进行发动机的剩余寿命预测之前，对于发动机多传感器数据，由于量纲不同，数量级不同，即使融合系数W可以调整传感器的量纲，并使其统一，也存在融合后的CHI数值过大的问题。此外，模型参数的微小误差将会对寿命预测结果产生较大影响，使得寿命预测精度不够高。为了解决不同传感器监测数据量纲和数据取值范围不一致的问题，论文采用归一化方法将传感器数据限定在[0,1]之间，即

(4)

1.3 基于线性维纳过程的发动机退化建模

实现了传感器数据的归一化后，便可对发动机进行退化建模，然后利用发动机历史寿命数据推导出发动机的预测寿命。

1.3.1 基于线性维纳过程的退化模型

针对线性退化设备而言，本文采用Wiener过程对CHI的演化过程进行建模，其表达式为

(5)

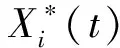
1.3.2 模型参数的极大似然估计

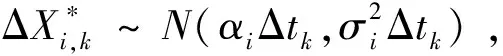
(6)

(7)

(8)

1.4 融合系数的确定

模型参数估计得到后，便可进一步推导出发动机的寿命，然后以发动机预测寿命与真实寿命的预测均方误差最小为目标函数，优化确定传感器的融合系数，实现CHI的构建。

1.4.1 发动机的寿命预测

对于式(5)给出的随机退化过程，在FHT的意义下，发动机的寿命可以定义为

(9)

式中：Ti为随机变量，为第i个发动机的寿命。

令Li,k为第i个发动机在tk时刻的剩余寿命，则其剩余寿命定义为

(10)

由于维纳过程首达阈值的时间和剩余时间都服从逆高斯分布(Inverse Gaussian distribution, IG)，因此可以得到发动机寿命T的概率密度函数为

f(t;αi,σi) =

(11)

由逆高斯分布的数字特征，可以得到发动机寿命的数学期望表达式为

(12)

1.4.2 求解融合系数

(13)

2 发动机的剩余寿命预测

针对具体运行的发动机(因此复合健康指标的退化量X*(t)下标不再有i，论文后面的退化状态也就都不再有下标i)而言，仍然采用Wiener过程对CHI的演化过程进行建模，其表达式为

(14)

2.1 参数估计

2.1.1 离线参数估计

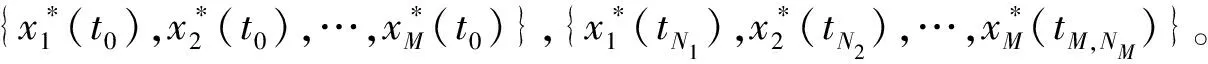
(15)

同时，σ为扩散系数，表述同类发动机之间的共同特性，即对所有发动机的CHI退化模型都是一样的，且

(16)

2.1.2 在线参数估计

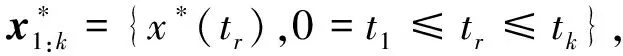
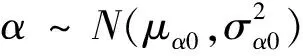
(17)

2.2 RUL的在线预测

根据式(10)，当不考虑漂移系数的随机特性时，由逆高斯分布的概率密度函数公式可以得到发动机剩余寿命lk的概率密度函数为

(18)

(19)

根据式(19)可以求得其数学期望为[21]

(20)

根据式(19)和式(20)可以确定任意tk时刻该发动机RUL的概率密度函数和均值，从而实现了发动机RUL的在线预测。

综上所述，论文提出的融合多传感器数据的发动机RUL预测方法的流程图如图1所示。

本文所提方法的具体实现步骤如下：

1) 求取融合系数：先将训练数据集进行归一化处理，然后根据多传感器数据融合公式，以真实寿命与预测寿命的预测均方误差最小为目标函数，接着通过非线性优化方法得到融合系数。

2) 离线估计先验参数：通过训练数据集离线估计漂移系数与扩散系数，并据此确定模型参数的初始值。

图1 RUL预测的流程图
Fig.1 Flow chart of RUL prediction

3) 实时参数更新：结合模型参数初始值和Bayesian公式，利用发动机实时监测数据实现模型随机参数的后验更新。

4) 剩余寿命预测：基于模型参数的后验更新，通过式(19)和式(20)得到发动机RUL的概率密度函数和均值。

3 实验研究

3.1 C-MAPSS数据集介绍

在实验中，基于文献[22]提供的涡扇发动机退化数据对论文所提出的方法进行验证。该数据是由C-MAPSS产生的，它被广泛用于各种工况下的发动机退化性能实验。图2为商用航空飞机燃气轮机的原理图。

图2 燃气轮机的原理图
Fig.2 Schematic diagram of a gas turbine

本实验采用C-MAPSS数据集中FD001数据集进行实验，数据集记录了发动机在单工况单故障情形下模拟产生的退化及失效数据，发动机在此运行条件下的模拟参数为：飞行高度0 m(海平面)，油门解析角度100°，马赫数Ma=0.84，故障发生位置为高压压气机(High-Pressure Compressor,HPC)[14,23]。FD001数据集包含了100个训练集、100个测试集和100个RUL 3部分数据。训练集包含了100个失效发动机数据：共有20 631组监测数据；测试集包含了100个退化发动机数据：共有13 096组监测数据；100个剩余寿命数据与测试数据集相对应，分别为每个测试发动机最后时刻的剩余寿命。其中，每一组监测数据包含了21个传感器的监测数据，传感器的具体信息如表1所示。

表1 21个传感器详细信息Table 1 Detailed description of 21 sensors

在每一个监测数据里都人工加入了大量随机噪声，并且该数据集存在一定的初始磨损，但是并不知道初始磨损程度如何，也未提供发动机失效阈值，为方便论文叙述，将表1中的传感器由上至下依次编号为1号传感器、2号传感器、…、21号传感器。同时，定义基于CHI的RUL预测方法为方法1，基于单一传感器的RUL预测方法为方法2。

通过采用论文提出的CHI构建方法，确定的21个传感器的融合系数如下：

由此得到相应的CHI监测数据如图3所示。由图3可知，CHI的监测数据存在较大的随机波动，因此论文采用MATLAB中的滤波函数，设置窗宽为10，对数据进行滤波预处理，滤波结果如图4所示。

为了对2种方法进行对比实验，对基于单一传感器的监测数据，论文采用同样的方法进行滤波预处理，设置窗宽为10，经过滤波后的21个传感器的监测数据如图5所示。

图3 CHI的监测数据
Fig.3 CHI’s monitoring data

图4 滤波预处理后的监测数据
Fig.4 Filtered pretreatment monitoring data

图5 滤波预处理后21个传感器的监测数据
Fig.5 Monitoring data of 21 sensors after filtering pretreatment

从图5中发现1号、5号、10号、16号、18号、19号传感器的监测数据并不存在。原因在于：这6个传感器的监测数据在发动机当前运行条件和故障模式下，随着发动机的动态退化过程并未变化，使得在归一化过程中，其分母为0，6个传感器归一化的结果为：NAN，因此其监测数据无法呈现在图形里。

3.2 相关系数的求解

另外，从图5中可以发现，随着发动机的退化，传感器监测数据的退化趋势和退化程度是有差异的。为了简化对比实验，本文将根据传感器监测数据与复合健康指标的相关性选取相关程度最高的2个传感器进行对比实验，即

(21)

表2 21个传感器的相关系数Table 2 Correlation coefficient of 21 sensors

从表2可以看出，9号与14号传感器的相关系数绝对值最大，相关系数越大说明传感器数据对发动机退化数据拟合程度越高，由于实验目的是为了验证方法1相对于方法2的RUL预测精度更高，因此，没有必要对21个传感器都进行RUL预测。所以，为了对比2种方法的RUL预测精度，论文中的实验选择了21个传感器中相关系数绝对值最大的2个传感器：Nc传感器和NRc传感器。

3.3 模型退化轨迹与真实退化轨迹的对比

根据论文提出的方法，对于CHI以及Nc传感器和NRc传感器的监测数据采用线性维纳过程进行退化建模，其模型参数设置如下：

根据以上模型参数设置，针对测试发动机的监测数据，采用Bayesian方法对模型参数进行更新，所得模型退化轨迹与真实退化轨迹如图6所示。

从图6可以看出，2种方法的前期模型退化轨迹与真实退化轨迹相差较远，但是，越到后期模型退化轨迹与真实退化轨迹差距越来越小。主要原因在于：根据历史数据估计得到的参数与发动机退化过程中的真实参数相比，误差相对较大；但随着实时监测数据的增多，对退化信息获取得越多，参数估计结果也就越准确，说明2种方法都能够拟合发动机的真实退化轨迹。为此，论文实验选择测试发动机最后9个寿命周期进行RUL预测。

图6 模型退化轨迹与真实退化轨迹的对比
Fig.6 Comparison between model and actual degradation path

3.4 RUL预测精度分析

2种方法下的剩余寿命预测值与真实值的误差如图7所示。从图7可以直观看出，随着监测数据的积累，红线相较于其他2条线更加贴近黑线，说明方法1的RUL预测精度比方法2的RUL预测精度高。2种方法下预测剩余寿命的概率密度函数随运行时间变化的结果如图8所示。

图7 剩余寿命预测值与真实值的对比
Fig.7 Comparison of RUL prediction value with actual value

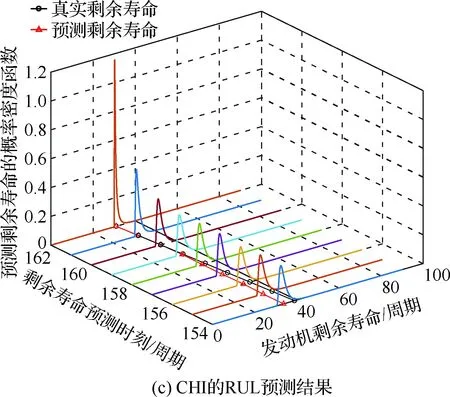
图8 两种方法下剩余寿命预测结果与真实值的对比
Fig.8 Comparison of RUL prediction value with actual value of two methods

图9 RUL预测的均方误差对比
Fig.9 Comparison of RUL prediction’s mean square error

根据图8预测的剩余寿命概率密度函数，可以计算剩余寿命预测的均方误差[17]。2种方法的RUL均方误差对比结果如图9所示。从图9可以发现，随着时间的推移，基于2种方法的RUL预测的均方误差都越来越小，但是方法1相较于方法2的均方误差略小。根据图9显而易见：3条曲线近乎是同步变化的，因此可以选择循环次数为118、119、120的3个点定量计算方法1的精度提高率。计算可得方法1相较于方法2中的Nc传感器和NRc传感器而言，其均方误差分别低1.69%与2.52%左右。实验结果验证了基于CHI方法的RUL预测准确性更高。由此可见，基于多传感器数据融合的RUL预测方法能够有效克服基于单一传感器的RUL预测方法在应用中面临传感器选择的难题，同时能够提高RUL预测的准确性。