基于ADAMS的FSAE赛车前悬架优化分析*

朱令磊，胡全，丁华锋,，陈加宾，路航

基于ADAMS的FSAE赛车前悬架优化分析*

朱令磊1，胡全2，丁华锋1,2，陈加宾1，路航1

（1.纯电动汽车动力系统设计与测试湖北省重点实验室，湖北 襄阳 441053；2.湖北三环锻造有限公司，湖北 襄阳 441700）

为了提高整车的操纵性，对悬架的设计进行仿真优化分析。基于Catia建立了FSAE赛车前悬架模型，观察其结构硬点，在Adams/car中建立FSAE赛车前悬架虚拟样机模型，进行平行轮跳仿真，选定优化目标；通过Adams/Insight对优化目标进行多变量优化设计，根据优化结果修改硬点参数值；再次进行平行轮跳仿真试验，对优化前后综合性能进行对比；优化后，四轮定位参数变化量明显变小，有利于赛车的操控稳定性。

FSAE；悬架系统；仿真分析；参数优化

前言

大学生方程式赛事即FSAE赛事创办至今已经三十多年的历史，旨在让大学生团队以一年的时间内，自行设计和制造一辆加速、制动、操纵性等性能有优异表现的赛车，并完成相应的所有项目。悬架作为底盘重要构件之一，其作用是传递、缓冲和减少各种工况路面下车轮传递给车架的震动和冲击，保证汽车平顺行驶[1]，故悬架设计的好坏对整车操纵性和稳定性有着重要影响。

在悬架性能优化方面，有很多国内外学者做出了研究[2,3]，但是通过数学函数表达式计算和优化设计，这样非常消耗时间和资源。近年来也有不少学者引进新的优化方案，刘伟的基于改进遗传算法NSGA-Ⅱ的悬架系统多目标优化策略[4]；蔡章林的基于VPD技术的整车试验优化[5]；解来卿引入神经网络控制方案开展优化[6]。

本文采用Adams/car软件对悬架系统进行优化设计，在软件中建立赛车虚拟模型，可进行相应工况的运动仿真，利用Adams/Insight针对各参数进行灵敏度分析并优化，达到设计目的，大大缩短了设计周期，提高设计效率[7]。

1 模型建立

FSAE赛车悬架多采用不等长双横臂独立悬架，多个节点是由SRSS结构构成[8]，结构示意图1如下，其中A点是车轮中心，B、C点是横臂与立柱连接的上下铰链，D、E是上横臂与车架的铰链，F、G是下横臂与车架的铰链，H是推杆与下横臂的铰链，I是推杆和摇臂的铰链，J是摇臂和减震器的铰链，K是摇臂和车架的铰链，L是减震器和车架的铰链，M为转向拉杆和立柱的铰链，N是转向拉杆和转向器断开点的铰链。

图1 双横臂悬架结构示意图

根据已在CATIA上建立的前悬架三维模型，以车架防侵平板下钢管中心为坐标原点，沿车身纵向为X轴，向后为负，沿车身横向为Y轴，向左为负，沿车身竖直方向为Z轴，向上为正建立坐标系，测得各节点处的硬点坐标，建立FSAE赛车仿真虚拟样机模型，如图2。

图2 双横臂仿真模型图

2 运动仿真分析

在仿真前，修改模型中四轮定位参数，并修改弹性文件，做到模型参数与FSAE赛车实际参数一致（数据如表1）。根据赛事规则要求，悬架跳动量至少为25.4mm，于是在Adams/ Car上进行车轮平行跳动仿真实验，跳动量为±30mm。仿真结束后，进入ADAMS/PostProcessor模块，由此得出了前轮定位参数随轮跳量的变化曲线[9]。

表1 前悬架硬点坐标值

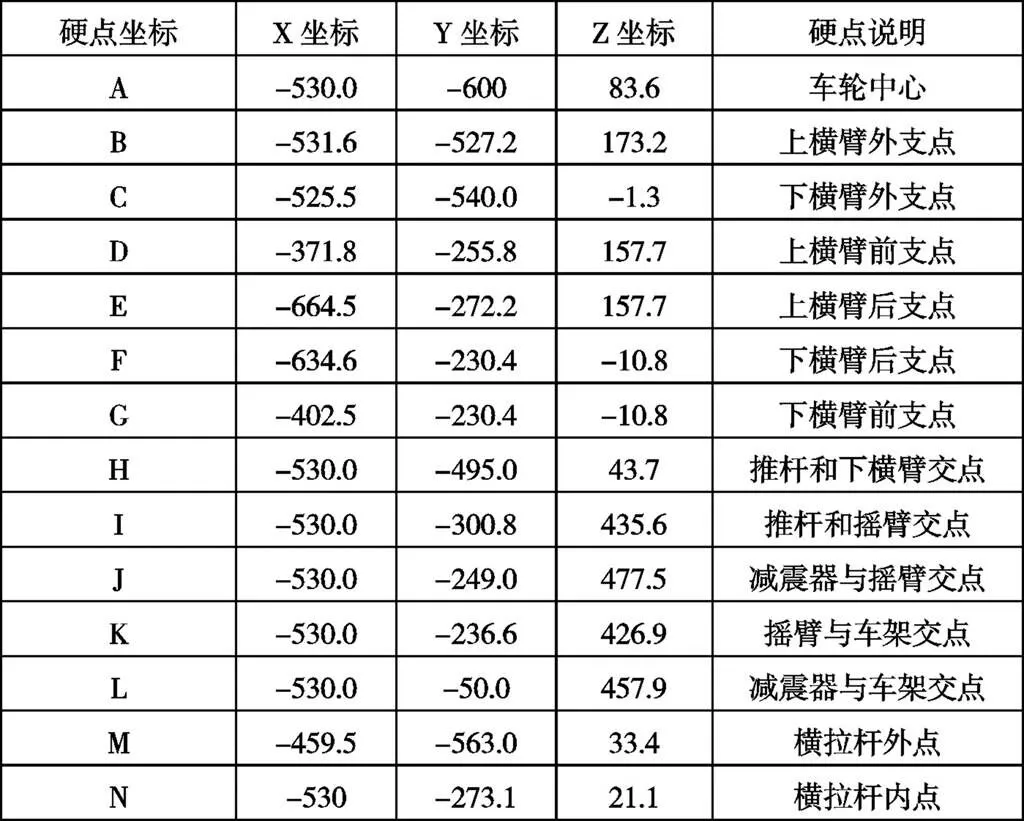
2.1 车轮外倾角

在赛车设计中，为了发挥轮胎的特性获得最大侧向力，一般设置成负外倾，而且希望外倾角变化尽可能小，减小轮胎磨损[10]。如图3所示，外倾角变化范围为（-1.328°~-0.841°），变化量为0.487°。

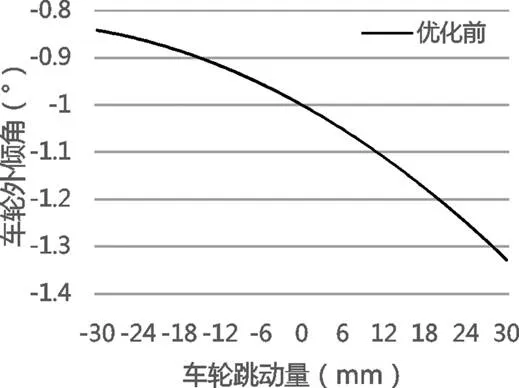
图3 车轮外倾角随轮跳变化曲线

2.2 主销后倾角

一定角度的主销后倾角可以增加赛车直线行驶的稳定性，并在转弯中产生一定的回正力矩，是赛车手转向轻便，增加驾驶体验。如图4所示，主销后倾角的变化范围为（-2.0448°~-2.008°），变化量为0.04°。

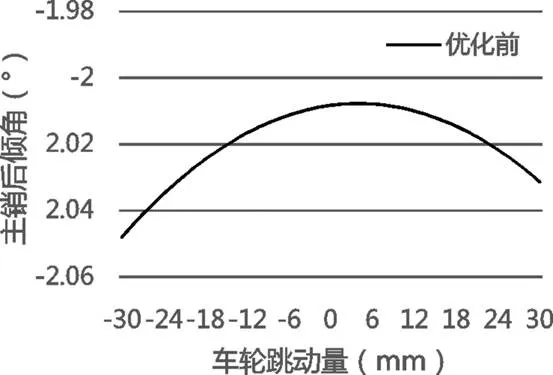
图4 主销后倾角随轮跳变化曲线

2.3 主销内倾角

主销内倾角的主要作用形成主销偏移距，产生回正力矩，使转向车轮自动会正，但是过大会造成转向沉重和轮胎磨损。如图5所示，主销内倾角的变化范围为（4.034°~4.506°），变化量为0.4722°。

图5 主销内倾角随轮跳变化曲线

2.4 前束角

因为负外倾的存在，车辆在直线行驶时会向偏向内侧，为了削弱这种趋势，采用负的前束角，保证车轮滚动和直线行驶，减小轮胎的磨损[11]。如图6所示，前束角的变化范围为（-1.269°~-0.836°），变化量为0.4334°。

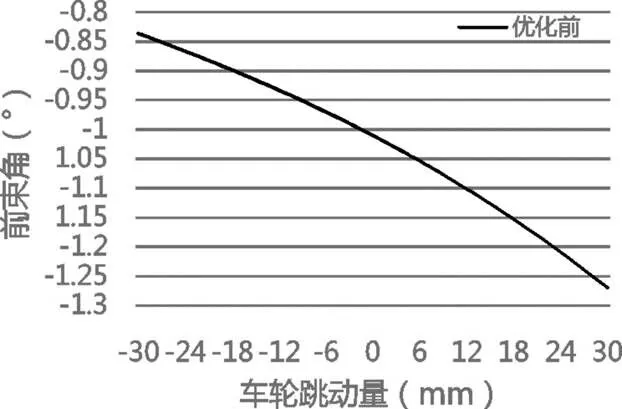
图6 前束角随轮跳变化曲线

3 参数优化分析

3.1 目标参数的选取

通过分析前轮定位参数随轮跳变化的规律，车轮外倾角、主销内倾角和前束角变化较大，主销后倾角变化较小。为了提升赛车悬架系统的性能，使赛车具有良好的操纵稳定性，需要对上述的定位参数进行优化设计。Adams/Insight正是用于参数化虚拟样机的多目标优化分析试验设计结果统计分析模块，具有强大的试验设计功能。运用Adams/Insight模块，对仿真结果进行优化处理，得到悬架硬点的最佳组合，达到提升操纵稳定性的目的[12]。

3.2 悬架模型灵敏度分析

选择上述定位参数作为设计目标。考虑到整车布置的限制，选择上横臂前点、上横臂后点、下横臂前点、下横臂后点和转向拉杆内点5个硬点，一般x坐标值对优化目标的影响比较小，所以选择这些硬点的y、z坐标作为设计变量，其范围为-5~5mm，然后再创建DOE矩阵，进行210=1024次迭代运算得到各坐标对目标的影响程度[13]。

Adams/Insight模块优化综合目标函数表达式：

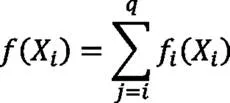
式中，(X)—优化目标（i=1，2，…，n）；X—输入变量；q—优化设计时所选定的目标个数；J—优化计算方程。(X)为悬架的前轮定位参数变化范围，作为输出的结果，X作为变量参数，可以是硬点坐标，螺旋弹簧的性能参数等。

3.3 悬架参数优化设计

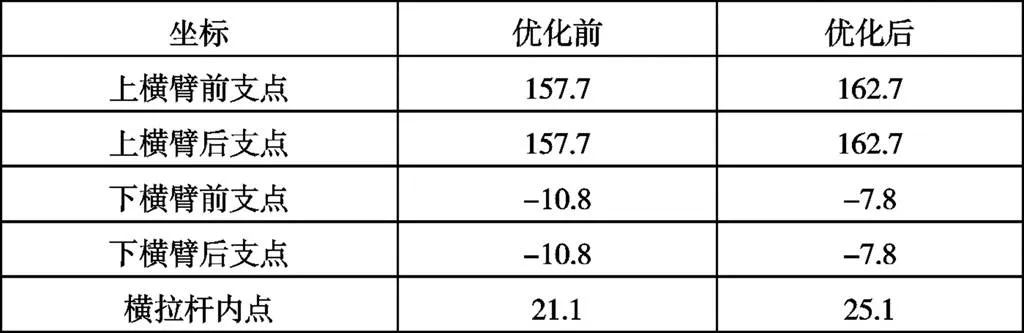
分析后发现对参数影响最大的是上横臂前点Z坐标、上横臂后点Z坐标、下横臂前点Z坐标、后点Z坐标和转向横拉杆内点Z坐标。根据影响程度对设计参数进行优化，优化前和优化后的坐标如表2所示：

表2 优化前、后硬点坐标对比

优化前、后悬架定位参数的变化对比图如图8-11，其中实线为优化前的变化曲线，虚线为优化后的变化曲线。

车轮外倾角：由图7可以看出，优化后的曲线变化范围为（-1.2561°~-0.9155°），变化量为0.3406°，比优化之前的0.478°减小了0.1374°，优化效果较为明显，有利于赛车的操纵稳定性。

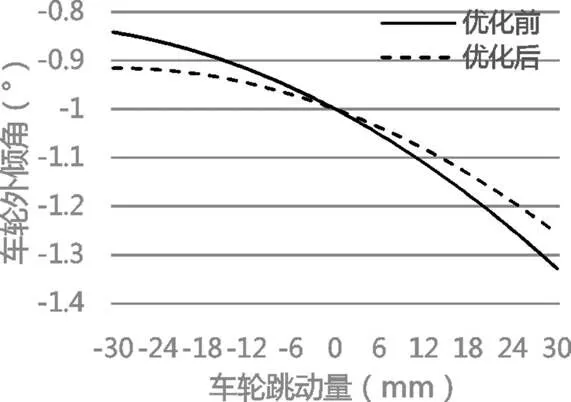
图7 优化后车轮外倾角对比图

主销后倾角：由图8可以看出，优化后的曲线变化范围为（-2.0543°~-2.0053°），变化量为0.049°，相比优化之前，增加了0.009°，增加量微小，符合设计要求。

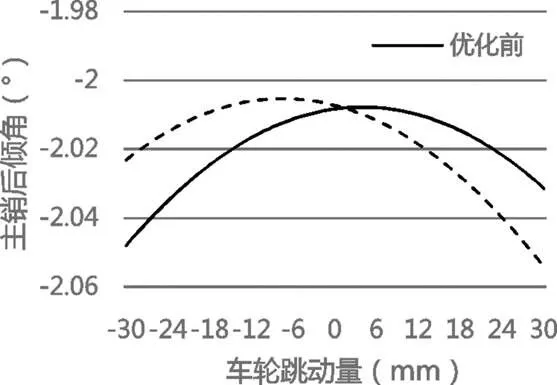
图8 优化后主销后倾角对比图

主销内倾角：由图9可以看出，优化后的曲线变化范围为（4.1093°~4.44°），变化量为0.3307°，比优化之前的0.4722°减小了0.1415°，变化量减少的同时，变化趋势仍符合随车轮上跳增加，随车轮下跳而减少的设计要求[14]，减小轮胎的磨损，增大了赛车的操纵稳定性。

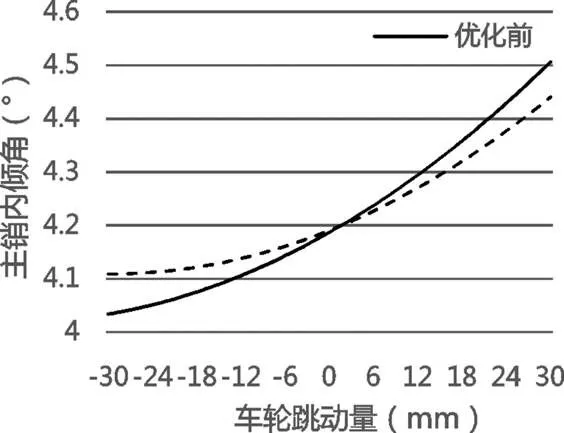
图9 优化后主销内倾角对比图

前束角：由图10可以看出，优化后的曲线变化范围为（-1.1919°~-1.0245°），变化量为0.1674°，比优化之前的0.4334°减小了0.266°，变化范围大幅度减小，且符合轮胎上跳呈减小的趋势，改善了车辆直线行驶时偏摆的情况，增大了赛车直线行驶的能力，减少了轮胎的磨损[15]。

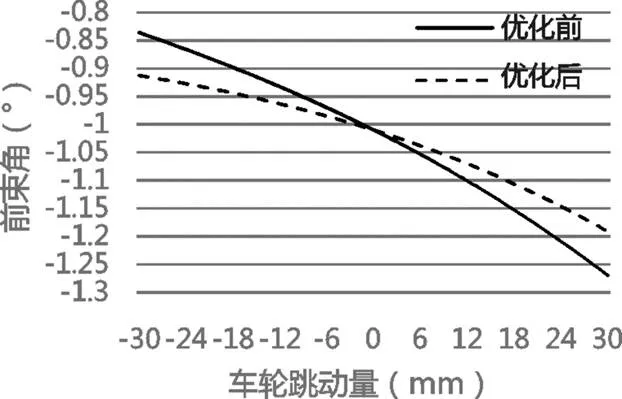
图10 优化后前束角对比图

4 结束语

本文通过Adams/car软件对FSAE赛车的前悬架系统进行优化设计，优化后的车轮外倾角变化减小0.1374°，减小了轮胎的磨损；主销后倾角变化虽然增加0.009°，但是变化范围和运动趋势仍符合要求；主销内倾角变化减小0.145°，减小了轮胎的磨损；前束角变化减小0.266°，保证了赛车的直线行驶能力。整体上来看，减小轮胎磨损的同时，增大了赛车的操控性稳定性，缩短了开发周期，为FSAE赛车悬架系统设计提供了参考。

[1] 刘伟,史文库,桂龙明,方德广,郭福祥.基于平顺性与操纵稳定性的悬架系统多目标优化[J].吉林大学学报(工学版),2011,41(05): 1199-1204.

[2] 褚志刚,邓兆祥,胡玉梅,熊伟.汽车前轮定位参数优化设计[J].重庆大学学报(自然科学版),2003(02):86-89.

[3] 段磊,刘绍娜,黄炯炯,杨耀祖.FSAE赛车车身与空气动力学套件设计及其仿真[J].汽车实用技术,2019(13):134-136.

[4] 刘伟,史文库,桂龙明,方德广,郭福祥.基于平顺性与操纵稳定性的悬架系统多目标优化[J].吉林大学学报(工学版),2011,41(05): 1199-1204.

[5] 蔡章林.基于VPD技术的悬架设计及整车试验优化[D].吉林大学, 2007.

[6] 解来卿,王良曦,李云超.基于ANN的汽车磁力悬架系统参数优化[J].车辆与动力技术,2005(03):32-35.

[7] 阮五洲.基于ADAMS悬架系统分析与优化设计[D].合肥工业大学,2008.

[8] 刘美燕.FSAE赛车悬架仿真分析及操纵稳定性虚拟试验[D].湖南大学,2008.

[9] 马玉坤,贾策,栾延龙,胡治国.ADAMS软件及其在汽车动力学仿真分析中的应用[J].重庆交通学院学报,2004(04):110-113+120.

[10] 宋学前,丁华锋,景文倩,黄成,朱令磊.FSAE赛车转向系统优化设计[J].重庆理工大学学报(自然科学),2019,33(02):38-44.

[11] 杨荣山.轿车底盘平台开发中多目标优化方法的研究及应用[D].华南理工大学,2009.

[12] 丁亚康,翟润国,井绪文.基于ADAMS/INSIGHT的汽车悬架定位参数优化设计[J].汽车技术,2011(05):33-36.

[13] 李嫚.FSAE赛车悬架的优化设计及分析[D].哈尔滨工业大学, 2011.

[14] 吴健瑜,罗玉涛,黄向东.FSAE赛车双横臂悬架优化设计[J].机械设计与制造,2011(10):120-122.

Optimization analysis of FSAE car front suspension based on ADAMS*

Zhu Linglei1, Hu Quan2, Ding Huafeng1,2, Chen Jiabin1, Lu Hang1

( 1.Hubei Key Laboratory of Power System Design and Test for Electrical Vehicle, Hubei Xiangyang 441053;2.Hubei Tri-ring Forging CO., LTD, Hubei Xiangyang 441700 )

In order to improve the maneuverability of the vehicle, the suspension design was simulated and optimized. The FSAE racing car front suspension model was established using Catia software. The hard points of its structure were observed. A virtual prototype model of FSAE racing car front suspension was established in Adams/car for parallel wheel jump simulation. Through Adams/Insight, multi-variable optimization design was carried out for the optimization target, and hard point parameter values were modified according to the optimization results. The simulation experiment of parallel wheel jump was carried out again to compare the comprehensive performance before and after optimization. Comparing the optimization results, the variation of four-wheel positioning parameters is significantly reduced, which is conducive to the control stability of the car.

FSAE;Suspension system;Simulationanalysis;Parameter optimization

U463

A

1671-7988(2019)24-118-04

U463

A

1671-7988(2019)24-118-04

10.16638/j.cnki.1671-7988.2019.24.038

朱令磊，男，本科，就读于湖北文理学院车辆工程专业，

丁华锋，博士，讲师，就职于湖北文理学院，研究方向：汽车系统动力学。

本项目受到湖北省教育厅科学技术研究项目（项目编号：Q20192605）资助。