基于曲率前馈的智能车辆路径跟踪算法
2019-12-27刘文涛
刘文涛
基于曲率前馈的智能车辆路径跟踪算法
刘文涛
(长安大学 汽车学院,陕西 西安 710064)
针对智能车辆直角转弯行驶工况,采用简化的车辆运动学模型,在纯跟踪控制算法的基础上进行改进,提出了一种基于道路曲率前馈的改进纯跟踪控制算法。采用基于道路曲率的纵向速度控制器,实时的根据车速计算出合理预瞄距离,依据预瞄点处的位置偏差得到合适的前轮转角,从而实现对路径跟踪的准确性。最后采用Simulink/Carsim联合仿真进行验证,结果显示该控制算法能够满足智能车辆在一定车速下对直角转弯行驶路径进行准确跟踪,具有良好的稳定性。
智能车辆;曲率控制;路径跟踪;纯跟踪算法
前言
智能车辆是当下国内外汽车行业新技术研发的重要阵地,包括谷歌在内的全球各大互联网和科研机构以及高校院所争相研究的领域。目前,针对智能车辆技术的研究主要集中在定位、感知、决策和控制等几个方面。而车辆本身作为一个非常复杂的运动物体,各系统呈现非线性的特点,导致了智能车辆在保持安全平稳路径跟踪控制方面一直存在较大困难。路径跟踪问题是智能车辆从定位感知决策等一系列功能实现之后,满足自主行驶的最后一步也是关系到车辆实际行驶表现的关键一步。基于预瞄式的路径跟踪算法因其既着眼未来又兼顾脚下特点受到研究人员的青睐。赵治国等人提出基于粒子群多目标优化算法的预瞄距离自适应驾驶员模型,该模型能在不同车速和道路曲率下同时兼顾跟踪精度、转向频度和稳定性[1]。陈无畏等人基于对未来路径的预瞄和当前路径的反馈设计预瞄加反馈控制器,该控制器能实现较小的跟踪误差且行驶更稳定[2]。而车辆在道路上行驶时,容易受到外界环境的干扰,加上车辆本身的系统特性,使得如何设计一种控制效果更好的智能车辆路径跟踪算法一直是研发人员争相解决的问题。
1 车辆运动学模型
车辆的运动学模型揭示的是车辆在全局坐标系下位置和姿态随车速和前轮转角之间的运动关系,建立合适的运动学模型能够更有效地设计路径跟踪算法。根据借鉴当下主流的低速工况下智能车路径跟踪车辆建模方法,本文采用简化后车辆只剩沿着x 和y 方向上的平移以及绕车辆z 轴的转动的车辆运动学模型。简单推导可得车辆运动学模型如下式:

式中φ为航偏角,X,Y分别为车辆后轴中心在惯性坐标系的横纵坐标值,l为车辆轴距,δ为车辆前轮偏角。
2 改进的纯跟踪算法
熟练的驾驶员在驾驶汽车时会根据车速不断地调整预瞄距离,车速低时降低预瞄距离,车速高时增加预瞄距离,从而保证车辆能够精确地跟踪参考路径。 因此仿照人类驾驶员的驾驶习惯,根据这一规律设计预瞄函数实现预瞄距离随车速的变化。为使车辆对预期轨迹信息的有效获取,预瞄距离随车辆纵向速度增加而增加:
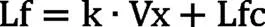
式中,k为预瞄增益,Lfc为静态预瞄距离。本次设计中k取值为0.2,Lfc取值为10m。
寻找当前车辆行驶位置距离参考轨迹中的最近一点,即车辆实际行驶轨迹和预期轨迹之间的欧氏距离:

式中,(cxi,cyi)为车辆当前行驶坐标,(cxj,cyj)为车辆预期轨迹坐标。参考轨迹上距离当前实际位置最近的一点即为预瞄点P。
α为航向偏差,在本文中为车辆行驶过程中实际坐标与预瞄点连线相对坐标轴行成的夹角与车辆本身航向角之间的差值。依据纯跟踪算法原理,为使车辆追踪到上文根据欧式距离计算得出的预期轨迹上的预瞄点P,该算法的实质是首先在目标轨迹上选取一目标点,用过车辆后轴中心点和目标点的一段圆弧来拟合实际的道路,据此可推得车辆的目标前轮转角为:

车辆在直角转弯过程中的速度控制采用基于道路曲率的反馈的速度控制器,由于直角转弯轨迹转弯时道路曲率很大,为保证车辆能够对预期轨迹的良好稳定跟踪,参考熟练驾驶员直角转弯时先减速进入弯道,过弯加速回到初始速度的车速控制,本次设计单独针对直角转弯行驶工况下设计考虑道路曲率的速度控制器。设置车辆初始行驶速度为30km/h,即为纵向车速所能达到的最大速度Vmax,此外由于本次设计中主要基于simulink和carsim联合仿真验证算法的有效性,车辆的加速动力性和制动系统的效率依carsim里的仿真车辆而定,为保证在速度控制器给出速度指令后仿真车辆能够较好进行速度跟踪,采用基于道路曲率前馈的纵向速度控制器,基本思路为道路曲率越大,纵向车速越小;反之纵向车速越大。采用前馈的速度控制器在道路曲率为零时,纵向速度达到最大Vmax,即为路径规划所得的纵向车速。道路曲率为ρ,此时纵向车速的计算公式为:

在给定路径规划的结果输入下,我们依据预瞄点处的道路曲率,得到无人驾驶车辆的纵向车速。针对直角转弯行驶工况,采用基于可变预瞄距离的纯跟踪控制算法,直角转弯行驶路径工况下,车辆纵向行驶速度采用上述速度控制器。在车辆行驶过程中,车辆控制器基于可变预瞄距离,根据车辆的实时运动状态信息和位置姿态信息比对预期行驶轨迹,从而计算出目标方向盘转角以保证车辆对预期轨迹的准确稳定的跟踪。
3 仿真验证
为验证本次基于道路曲率前馈的改进纯跟踪控制算法的有效性,采用matlab/simulink和carsim联合仿真,在同一行驶工况下对比传统纯跟踪算法和本文改进后的算法。其中carsim里面车型选择“B-Class Hatchback2012”,进行整车参数设置,在直角转弯道路设置时,其中车道总宽为7m,直角转弯处道路半径设置为7m,基本满足直角转弯道路环境条件。仿真验证过程如下:分别在传统的纯跟踪算法和上文的改进算法的控制下跟踪规划路径,对比两种算法在路径跟踪精度和车辆行驶稳定性方面的差异。仿真时间为30s,仿真步长为0.025s,距离单位为m,速度单位为km/h。
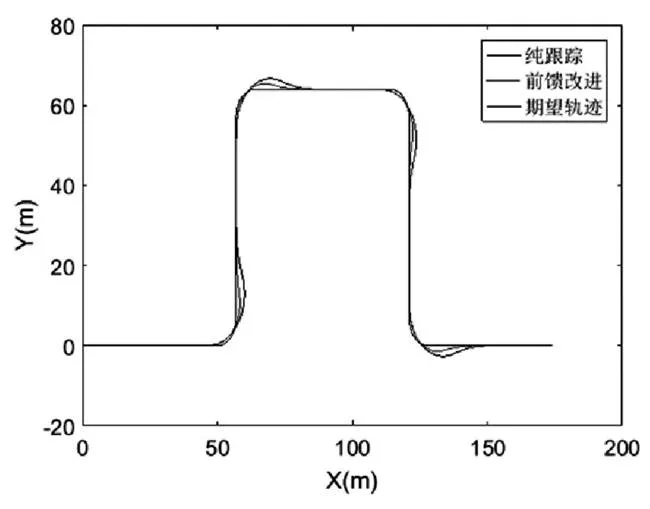
图3 两种算法下跟踪期望轨迹示意图
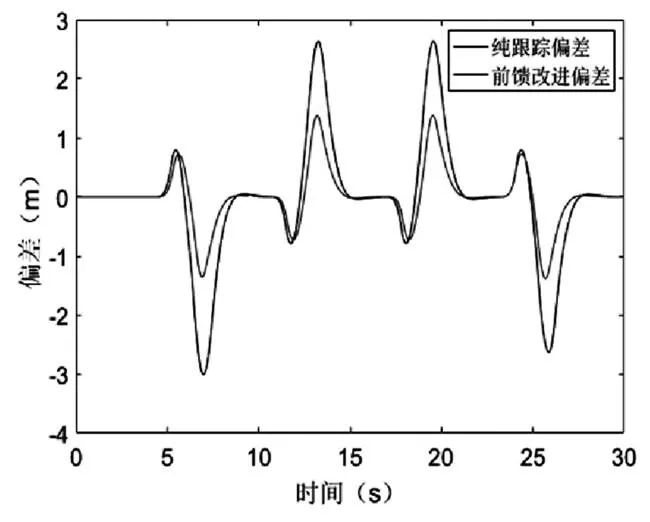
图4 两种算法下横向跟踪偏差示意图
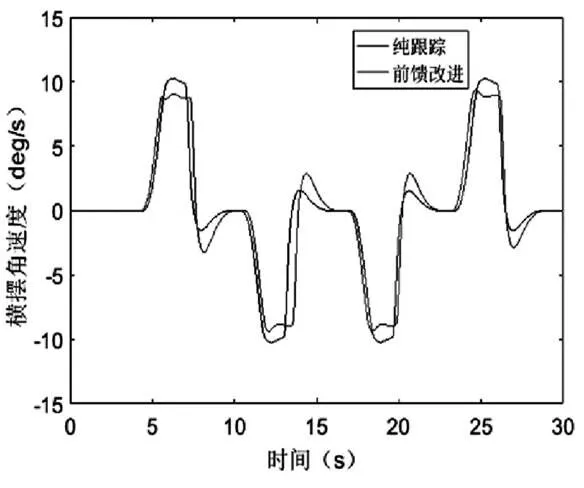
图5 两种算法下车辆航偏角对比示意图
4 结论
由上文的仿真结果图我们可以看出,在车辆进行连续四个直角转弯路径行驶时,改进后的算法在路径跟踪的精度明显好于传统跟踪算法,并且改进后,车辆在转弯过程中的横摆角速度较传统跟踪算法小,车辆行驶更为平稳。因此基于道路曲率前馈的改进纯跟踪控制算法在跟踪精度和保持车辆稳定性方面更有优势。
[1] 赵治国,周良杰,朱强.无人驾驶车辆路径跟踪控制预瞄距离自适应优化[J].机械工程学报,2018,54(24):166-173.
[2] 陈无畏,李进,王檀彬,李碧春.视觉导航智能车辆的路径跟踪预瞄控制[J].机械工程学报,2008(10):277-282.
[3] 郭景华,李克强,罗禹贡.智能车辆运动控制研究综述[J].汽车安全与节能学报,2016,7(02):151-159.
[4] 郭应时,蒋拯民,白艳,唐杰帧.无人驾驶汽车路径跟踪控制方法拟人程度研究[J].中国公路学报,2018,31(08):189-196.
Path Tracking Algorithm of Intelligent Vehicle Based on Curvature Feedforward
Liu Wentao
( School of Automobile, Chang'an University, Shaanxi Xi'an 710064 )
Aiming at the right-angle turning condition of intelligent vehicles, using a simplified vehicle kinematics model to improve the pure tracking control algorithm. An improved pure tracking control algorithm based on road curvature feedforward is proposed. A longitudinal speed controller based on road curvature is used to calculate a reasonable preview distance according to the vehicle speed in real time, and a suitable front wheel angle is obtained according to the position deviation at the preview point, thereby realizing the accuracy of the path tracking. Finally, Simulink/Carsim joint simulation is used to verify the results. The results show that the control algorithm can meet the intelligent vehicle's accurate tracking of the right-angle turning path at a certain speed, and has good stability.
Intelligent vehicle; Curvature control; Path tracking; Pure pursuit algorithm
V323
B
1671-7988(2019)24-31-03
V323
B
1671-7988(2019)24-31-03
10.16638/j.cnki.1671-7988.2019.24.010
刘文涛,硕士研究生,就读于长安大学汽车学院车辆工程专业。
