一种基于遗传算法的NIC-SoS发展路线图优选方法

禹明刚 牟杨城 康凯

网络信息体系(Networking Information-Centric System of Systems,NIC-SoS)[1-3]是近年来我军在网络化和体系化作战背景下提出的新概念,这一体系是一个由跨接多个“域”(Field) 的军事信息装备,以及由多种信息装备铰链而成的网络共同构成的复杂巨系统,其实体关系概念图如图1所示.

不同种类、规模的信息装备,及装备间的组网关系形成不同的网络信息体系方案,具备不同的作战能力.随时间推进,各体系方案由于自身结构调整(装备增减、更替、连接关系重构等) 引发能力的演化(提升、削弱、消退等).前期,我们对网络信息体系的演化机理及规律进行了初步探索,相关成果见文献[4-7].如何寻找一种科学方法来评估体系方案在演化各时间剖面上的能力,且综合各阶段评估结果选择最优体系发展路线图,具有重要科学意义和应用价值.

1 NIC-SoS 发展路线图优选问题建模

设网络信息体系发展过程分L(L∈Z) 个阶段,每个阶段存在wl(wl∈Z,l∈Z,l∈[1,L])个可行方案,第l阶段的方案表示为Swll,则网络信息体系发展路线图如图2所示.

由图2可知,网络信息体系发展路线图的优选问题是一个复杂的多阶段、多属性决策问题,本质上是从众多可行的体系发展路线中,搜索最优体系发展路线的问题.

前期,我们曾经从能力视角对某时间阶段内体系方案的效用值进行瞬态评估[8],进而可以得出该时间段最优的体系方案.然而,相邻阶段的体系方案演化过程需要承担必要的演化代价(时间、费用、风险等),每个时间阶段的“局部最优”体系方案构成的发展路线不必然是“整体最优”[9-11].因此,需要设计一种路线图优选方法,综合评估体系发展各阶段效用值,并基于评估结果,在众多体系发展路线图中寻找最优解.

网络信息体系发展路线图优选问题数学模型的优化目标,是极大化网络信息体系发展路线图的综合效用值.我们拟从3 个方面考察网络信息体系发展路线图的综合效用(Utility): 周期内各阶段能力需求满足度均值E(C)、周期内能力需求满足度震荡程度σ2(C)、周期内方案演化总代价Cost_all.

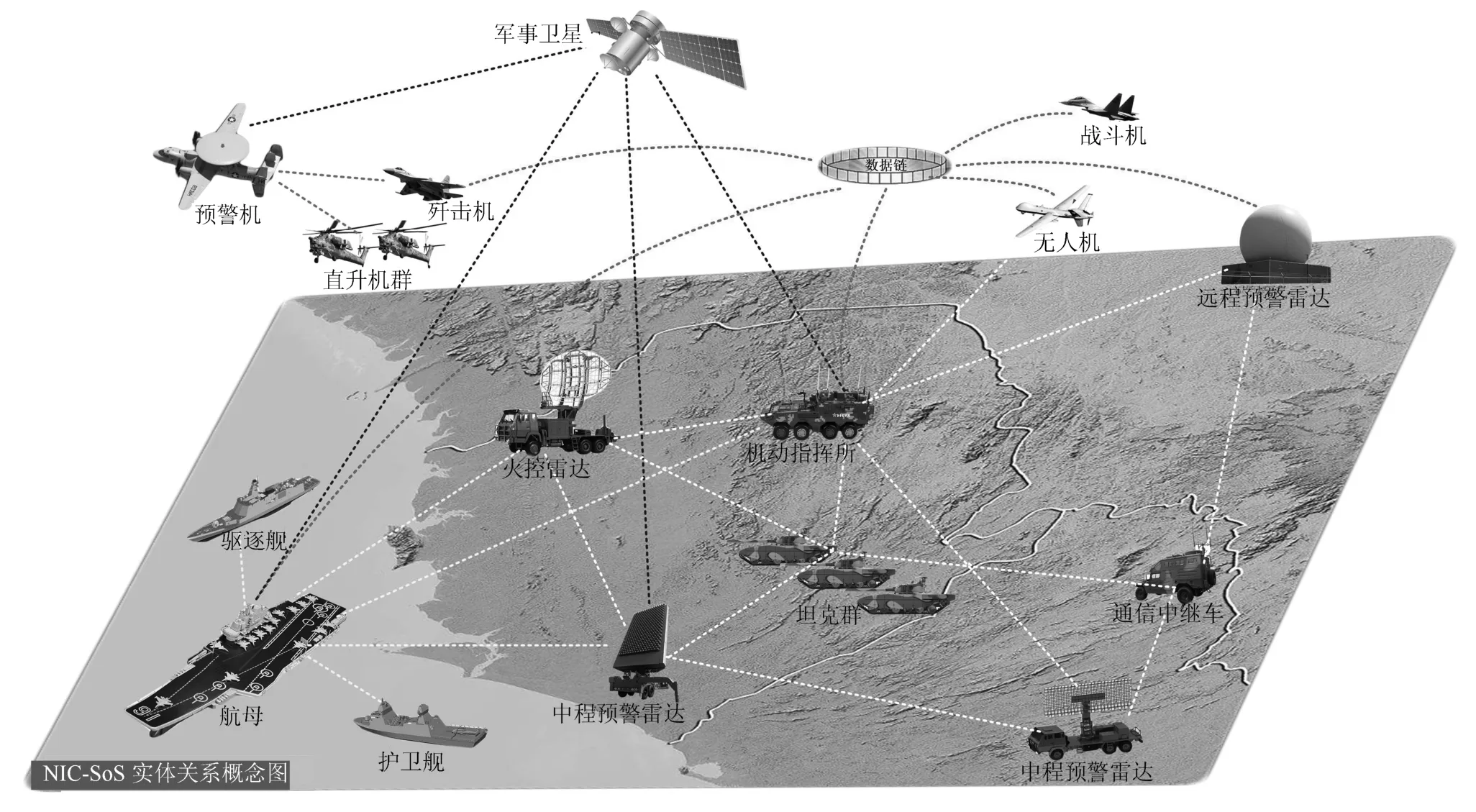
图1 网络信息体系实体关系概念图

图2 网络信息体系发展路线图示意图

设网络信息体系发展路线图为体系方案的序列:

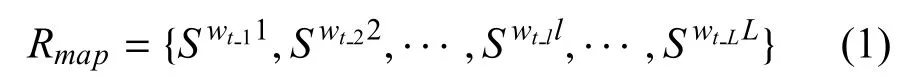
其中,Swtll(wtl∈[1,wl],l∈[1,L])表示体系发展路线图在第l阶段所有可行的wl个体系方案中选择了第wt-l个.

网络信息体系是一种“以能力为牵引”的建设思路,建设目的是保证体系能够满足遂行特定使命任务的能力需求[12-14].因此,定义体系方案在演化各阶段的瞬态能力满足度为S(Swtll),则整个演化周期内体系能力满足度均值为:

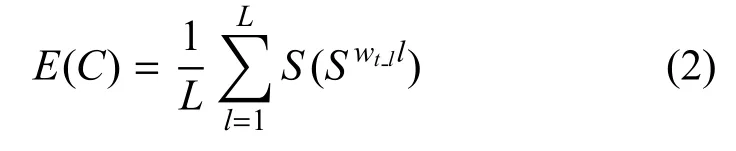
网络信息体系发展路线图的效用评价是一个动态过程,既需要考虑路线图在整个演化周期内的平均能力满足度,又要考虑满足度的稳定性.一条稳定性较差的体系发展路线图意味着体系能力建设的不均衡不稳定,能力建设的随意性较大.用方差表征路线图在周期内能力需求满足度震荡程度:

设相邻阶段体系方案能力演化代价为Cost(Swtll→Swtl+1l+1),则整个路线图中体系方案能力演化总代价为:

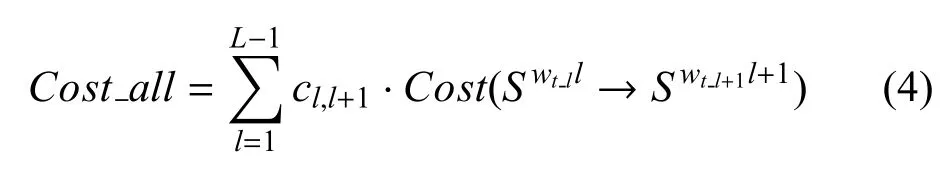
其中,cl,l+1为Cost(Swtll→Swtl+1l+1)的权重,表明评价过程中对不同演化时刻的重视程度.

设上述3 类指标权重为αi(i= 1,2,3),且将能力满足度方差σ2(C)、能力演化总代价Cost_all两类成本型指标归一化为效益型指标σ2(C)∗、Cost_all∗.

综上所述,网络信息体系发展路线图最优选择问题,以体系方案发展路线Rmap为决策变量,其数学模型为:

2 基于遗传算法的最优发展路线图搜索

智能搜索算法为自然启发式搜索方法,不需要描述优化问题的整个解空间,利用种群对解空间进行抽样筛选,并通过各种算子操作使种群在迭代过程中逐渐聚集到产生高质量解的区域.本文采用遗传算法(Genetic Algorithm,GA) 来搜索网络信息体系发展的最优路线图.

2.1 染色体编码及适应度函数

一条网络信息体系发展路线即为一个长度为L的体系方案序列组合.本研究采用整数型编码方式对发展路线进行染色体编码: 一条染色体就是一条体系发展路线,它由L个整数构成有序序列:

其中→[1,wl],l→[1,L].序列中的wtl表示体系发展路线在第l阶段所有可行的wl个体系方案中选择了第个.

根据式(4),一条染色体性能优劣的评判标准是该染色体对应的体系发展路线图的综合效用值.路线图的综合效用值越大,其对应的染色体性能越优.因此,设置染色体的综合效用值F为GA 的适应度函数:

2.2 遗传算子

1)交叉算子

随机产生初始种群ΔI,|ΔI| =N,计算ΔI中各染色体适配值.设置适配值较差的染色体交叉概率为Pc1,适配值较优的染色体交叉概率为Pc2,且满足Pc1＞Pc2.计算染色体发生交叉操作的概率Pc为:

其中,f为交叉操作中适配值较大的染色体的适配值,为ΔI的平均适配值,fmax为ΔI中最大的适配值.

采用轮盘赌选择法进行M(M∈[1,N]) 轮选择,选中的染色体对参与交叉操作.设参与交叉操作的两条染色体分别为和令x=Random[2,L],基于以下原则产生新的染色体和J′=

设未参与交叉的染色体共N0个,保留该N0个未参与交叉的染色体,并从交叉产生的新染色体中随机选择N-N0,产生交叉种群ΔC.

2)变异算子

设适配值较差的染色体变异概率为Pm1,适配值较优的染色体变异概率为Pm2,且满足Pm1＞Pm2.计算染色体发生变异操作的概率Pm为:

其中,f为待变异染色体的适配值,为ΔI的平均适配值,fmax为ΔI中最大的适配值.

采用轮盘赌选择法进行M(M∈[1,N]) 轮选择,选中的染色体参与变异操作.对于染色体I=基于以下原则进行变异产生新的染色体

设未参与变异的染色体共N0′个,保留该N0′个未变异的染色体,并与M个新变异产生的染色体共同产生变异种群ΔM.

3)选择算子

选择操作是依据适配值函数为每一条染色体计算适配值,从而使较优的染色体保留下来.然而,在生物界遗传过程中,最优染色体并不总是被保留,因此,不能完全按适配值大小的顺序进行优选.在具体的操作中,为每条染色体设定选择概率,保证每条染色体存在被保留的可能性.同时,设定适配值越大的染色体保留概率越大,实现优化遗传的目的.

将ΔI、ΔC和ΔM合并为一个种群,计算合并种群中每个染色体的适应度值fn,其中h∈[1,3N].则保留概率

使用精英保留策略和轮盘赌选择相结合的方法进行选择操作,保留pn值最高的前M(M∈[1,N])条染色体,对合并种群中剩余染色体进行N-M轮轮盘赌选择,生成新一代种群ΔN.

2.3 算法步骤

基于GA 的网络信息体系发展路线图优选方法流程如图3所示.

3 建模方法比较

基于GA 的网络信息体系发展路线图优选算法如下:

Step 1设置种群规模N,采用整数型编码方式对染色体进行编码,随机产生初始种群ΔI;

Step 2依据交叉概率Pc,对ΔI进行交叉操作,产生交叉种群ΔC;

Step 3依据变异概率Pm,对ΔI进行变异操作,产生变异种群ΔM;

Step 4将种群ΔI、ΔC和ΔM并为一个种群,进行选择操作,产生新一代种群ΔN,并替代ΔI;

Step 5重复Step2 至Step4 直至达到算法终止条件.

图3 基于GA 的体系发展路线图优选流程

4 算例仿真

网络信息体系4 阶段动态演化路线中,第1 阶段可选的体系方案分别为S11-S31,第2 阶段为S12-S62,第3 阶段为S13-S53,第4 阶段为S14-S44.采用文献[15] 提供的方法,计算各阶段方案的能力需求满足度如表1所示.

在网络信息体系演化过程中,相邻阶段之间会产生包括经费投入等在内的演化代价,以前两阶段为例,给出方案间演化代价如表2所示.

表1 各阶段方案的能力需求满足度

表2 第1 阶段与第2 阶段间体系演化代价

根据式(4)建立的数学模型,利用GA 对4 个阶段的演化路线进行最优化选择.取α1= 0.30、α2=0.35、α3= 0.35,设GA 算法种群规模N= 100,交叉概率Pc1= 0.75、Pc2= 0.60,变异概率Pm1=0.80、Pm2= 0.70,轮盘选择轮数及保留算子中M= 30,算法终止条件为适配值最大的染色体连续50 代适配值不变.

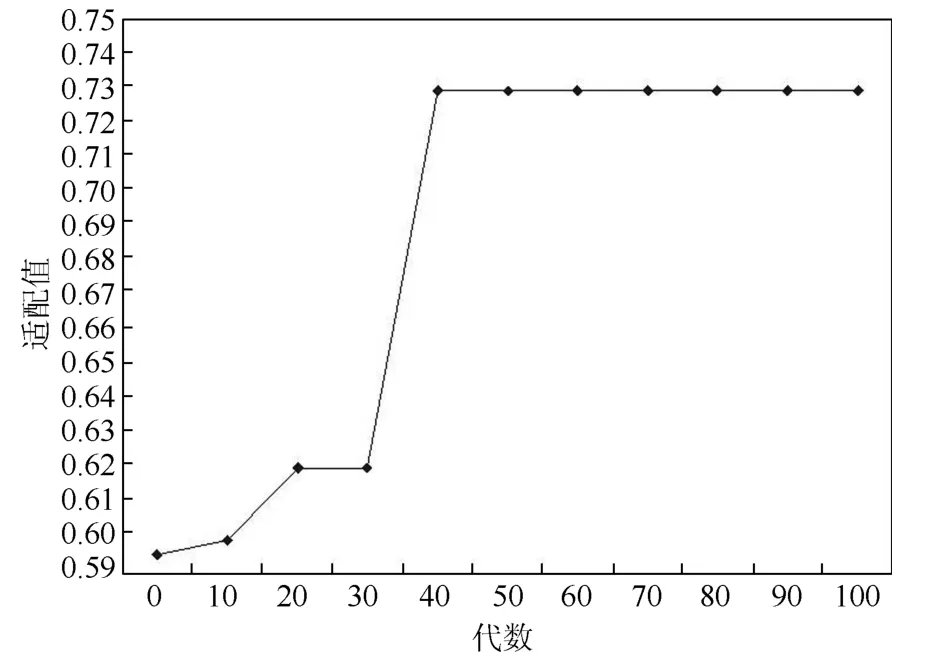
图4 遗传算法解的收敛情况

随着迭代次数增加,GA 收敛情况如图4所示,遗传算法在第43 代收敛到最优解,其适应度值为0.73,即综合效用值为0.73.其最优解为S21→S42→S13→S34.

5 结论

本文针对网络信息体系发展路线图优选问题,建立了网络信息体系发展路线图优选问题模型,设计了基于遗传算法的最优发展路线图搜索策略.算例仿真表明,遗传算法能够有效实现网络信息体系发展路线图的优选.

网络信息体系对我军联合作战体系的形成和效能的发挥起着全局性、基础性的支撑,如何寻找一种科学方法对网络信息体系进行方案评估、优选及发展路线设计,具有重要科学意义和应用价值.下一步笔者拟结合网络信息体系的军事领域特点,考虑体系优选中的敌我对抗因素,引入博弈理论[16],实现对抗环境下的网络信息体系方案评估及优选,为我军科学合理地进行网络信息体系顶层设计提供决策支持.