基于LSTM网络的短波天波信道分析及预测∗

赵四方 马启原 李铁楠

（1.中国人民解放军92785部队 绥中 125200）（2.中国人民解放军91404部队 秦皇岛 066001）

1 引言

短波通信具有开通快，抗毁性强和维护费用低的特点，各国军队均进行了广泛的研究。远距离短波通信主要是依靠天波传播的，其通信效果与电离层的变化特性有关，而电离层的反射特性是随着时间、地点、频率、季节、年份等不断地变化的，属于时变色散信道，一天之中的变化也是很大，它同时具有时间、频率、空间三种选择性衰落，且受太阳活动周期影响，这给短波通信资源的调度使用带来了很大的不确定性。针对频率的预测主要采用电离层预报模型。然而，传统电离层的预报模型无法针对确定的天波电路模型进行分析。在具体短波天波通信时，迫切需要一种可以实现点对点的天波电路精准分析预测的模型［1～2］。

近几年海军的远海活动次数不断增加，积累了大量的远海短波通信数据，反映了我海军当前情况下真实的通信技术水平。在传统理论计算方法与探测评估方法未能发挥需求作用的情况下，采用人工智能的方法，实现对历史通信数据的有效利用，从历史数据中总结出短波通信信道蕴藏的通信规律，探索基于人工智能技术辅助的通信组织方法，可为海军短波通信资源调度使用提供辅助决策支撑。

2 相关概述

短波的天波通信是通过电离层的反射实现远距离通信，电离层是影响短波天波通信质量的关键，其中包括电离层的昼夜特征、太阳黑子数目变化，工业电气电磁噪声等［3］。电离层参数预报方法很多，其中国际参考电离层模型IRI因其用途的广泛性和在电离层研究领域的重要性，成为为电离层参数的国际技术标准。然而，传统电离层的预报模型无法针对确定的天波电路模型进行分析［4］。在具体短波天波通信时，迫切需要一种可以实现点对点的天波电路精准分析预测的模型。为此文献［5～7］均通过使用神经网络方法实现短波天波信道的频率预测。然而，以上文献所使用的神经网络算法均不具有记忆性，无法对随时间序列变化的模型进行有效研究，因而无法得出天波电路的慢变化与快变化规律。

本文采用多层神经网络算法，第一层长短期记忆网络（Long Short-Team Memory，LSTM），是时间递归的神经网络，属于递归神经网络中的一类，较BP神经网络具有记忆性，更易处理与时间序列相关的问题。在LSTM网络中存在三个逻辑门，分别为输入门，输出门与遗忘门。逻辑门通过固定的计算方法，分别实现LSTM网络基本神经结构Cell对信息的接收，输出与遗忘三个过程［8］。由于LSTM网络具有递归性，选择性输入与输出的特征，符合短波天波通信过程中分析信道变化性时的时间迭代性要求。

第二层深度神经网络［9］（Deep Neural Network，DNN）是在感知机的基础上组成，在网络中加入了隐藏层，实现了神经网络的多元输入与多元输出。深度神经网络按照结构划分为输入层，隐藏层与输出层。深度神经网络中，每个感知机之间互相连接，故深度神经网络又称为全连接网络［11］。本文中，DNN层作用是将LSTM层高维度堆叠序列转化为与样本相同的标准输出序列，从而得到短波天波电路变化规律的预测结果。

在多层神经网络训练中，为避免梯度下降时达到局部极值点，使用小批量梯度下降法优化神经网络训练过程，利用Adam方法优化训练器，并在该方法下测试平方和误差函数与交叉熵误差函数，以确定合适的损失函数。为避免模型出现过拟合现象，训练过程中设置神经元以一定概率不参与神经网络的训练。

3 多层神经网络的短波天波电路建模原理

神经网络将短波天波电路的通信过程视作“黑箱”分析。由于发方固定站的通信设备参数资料不易获取，故仅考虑接收方站相关参数变量。其中短波天波模型的无关变量为接收机地点、接收机型号以及接收天线型号；有关变量包括发射机位置，接收日期、接收时间、接收功率与接收信号强度。其中日期与接收时间两个变量在模型建模中各自分开作为一个单独变量，在变化规律分析过程中作为一个整体变量。本方案中，数据预处理，经过LSTM网络与DNN网络计算输出结果。模型根据预测值与真实值的误差结果确定神经网络最优参数。最终与其他短波预测软件进行比较，得出结论。流程如图1所示。

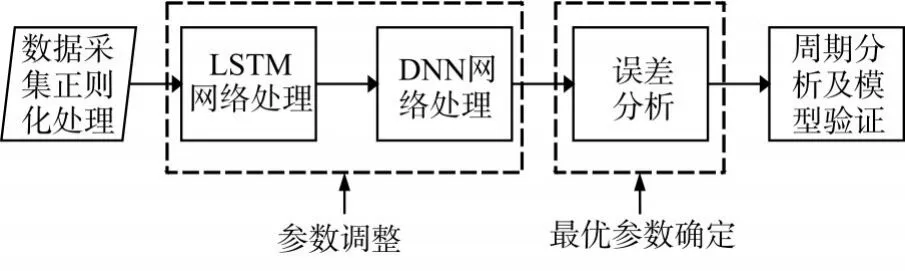
图1 方案流程图

3.1 数据采集

方案通过查找国际短波频率表，定位发信台站的发信频率及时间，通过接收设备接收模拟进行短波通信过程，并对接收信号进行记录。其中记录的主要内容包括：

1）信号的通信频率，其频率范围为3MHz～30MHz。

2）信号的接收带宽，按照国际标准，信号的接收带宽设置为3.3kHz，频率划分成为8100个不同的信道。

3）信号的采集周期，信号的采集周期根据采集时间变化。

4）信号的采集时间段。

5）信号的接收功率，接收信号功率单位为dBm。

将采集到的信号按照时间序列排列，将样本数据进行正则化处理。

3.2 神经网络权值初始化方案

隐层神经元的权值初始值决定了神经网络的初始结构和是否能达到梯度最小值的情况。

神经网络隐层权重的迭代过程会因为激活函数不同而存在梯度消失（Vanishing Gradient Problem）和梯度爆炸（Exploding Gradient Problem）情况。由于logistic函数的均值总是大于0，导致隐层神经元趋于饱和，使用Xavier［12］方法，要求神经元的初始值应服从：

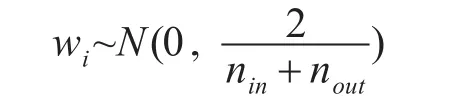
假设偏置为0，输入为1，神经网络学习速率为η，求得神经网络迭代公式为

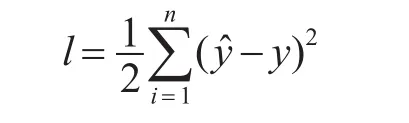
LSTM网络使用logistic函数σ，神经网络权值为W ，偏置为b，输入为X，故公式为

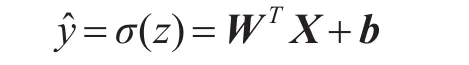
其中nin与nout表示输入层神经元个数与输出层神经元个数。神经网络偏置b的维度为（1，n），其中n代表下一神经层中神经元个数，偏置b的分布可以不做要求。

3.3 神经网络损失函数

神经网络的权值优化过程首先需要确定损失函数。损失函数包括平方和误差函数（error sum of squares）与交叉熵损失函数（cross-entropy error）。

假设ŷ表示神经网络输出值，y表示真实值，平方和误差函数l的公式为

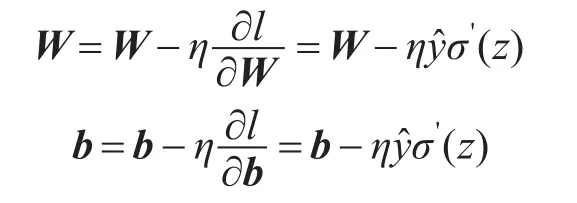
3.4 神经网络训练器优化方案

优化器选择Adam（Adaptive Moment Estimation，Adam）方法。其结合了Monentum和RMSProp的优化方法，保留了梯度下降时的动量保持情况，同时其利用梯度的一阶矩阵估计与二阶矩阵估计动态调整不同参数的学习速率［10～11］。假设其保持动量的能力为β1，一般情况下β1=0.9；梯度的二阶估计为s，衰减速率为β2，一般情况下β2=0.999；⊗表示元素乘法，⊘表示元素除法，ϵ为平滑变量，防止出现除以0的情况，一般情况下ϵ=10-8。公式为

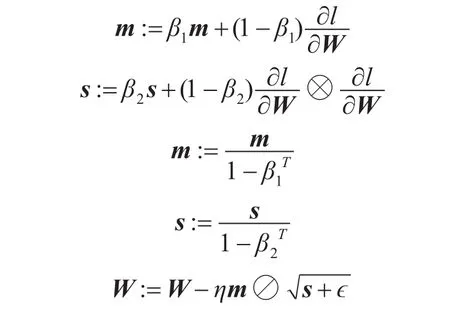
在训练过程中采用小批量梯度下降算法（Mini-batch Gradaient Descent）。小批量梯度算法将数据划分为多个不重合的数据子集，每一个子集作为一组训练集进行训练。相较于梯度下降算法，小批量梯度下降算法在训练模型时具有更高的训练效率与速度。

3.5 神经网络结构设计

LSTM神经网络结构包括时序（Sequence）与隐层神经网络（Hidden Layer）结构。隐层神经网络数目和神经元数目根据具体要求分为两种情况。根据网络的复杂度不同，神经网络层数可以选择平行关系的设计思路和递进关系的设计思路。本文采用递进关系设计的多层神经网络，其中第一层LSTM层用于短波天波模型的时间变化规律分析；第二层采用深度神经网络，用于对第一层输出结果的抽取与标准化处理。其中LSTM神经网络在多层神经网络中发挥核心作用。

为了降低模型的过拟合风险，提高神经网络的训练速率，采用Dropout Regularization的方法有效提高神经网络的准确率。Dropout Regularization实质是在每一次训练中，除输出层以外的神经元都以概率p不参与神经网络的计算，鉴于每次有部分神经元不参与训练，故使得每个参与训练的神经元泛化性与神经元之间的合作更为紧密，对数据的细微变化不过于敏感。一般情况下p=0.5，实际工程中将根据模型反馈结构进行适当调整［13～14］。

4 短波天波电路的多层神经网络模型

4.1 数据准备及预处理

样本数据经正则化处理后，选择每组样本数据的序列长度，并将样本数据划分为训练集

与测试集，满足数据量比例为2：1。其中训练集数据分为两组，一组为X数据，另一组为Y数据，测试集数据划分方法同训练集数据。划分算法如下。

输入：样本数据data

输出：训练集train_X，train_Y，测试集test_X，test_Y

步骤：（1）读取样本数据data；

（2）样本数据正则化处理，得到数据normalized_data；

（3）计算训练集数据长度 L1，测试集数据长度L2；

（4）for(索引=0，索引＜ L1-序列长度-1，索引=索引+1){

数组X=normalized_data[索引：索引+序列长度]；

数组Y=normalized_data[索引+1：索引+序列长度+1]；

添加一组X数据于train_X列表中；

添加一组Y数据于train_Y列表中；

}；

（5）for(索引=L1，索引＜ L1+L2-序列长度-1，索引=索引+1){

数组X=normalized_data[索引：索引+序列长度]；

数组Y=normalized_data[索引+1：索引+序列长度+1]；

添加X数据于test_X列表中；

添加Y数据于test_Y列表中；

}；

（6）更改train_X，test_X维度[-1，序列长度，输入数据长度]；

更改train_Y，test_Y维度[-1，序列长度，输出数据长度]；

4.2 LSTM神经网络搭建及训练

本方案采用四层神经网络结构，按次序分别为输入层（input_layer），隐层神经网络1（hidden_layer1），隐层神经网络2（hidden_layer2）与输出层。其中输入层输入数据为train_X或test_X，通过神经网络计算得到预测数据，通过损失函数与梯度下降算法实现神经网络模型的优化。将准备的数据划分为多个子数据集，使用Mini-batch算法进行网络训练。

输入层神经网络在训练过程中使用Dropout方法，设置输入神经元的损失概率为20%。在测试过程中输入层神经元为全连接状态。隐层神经网络1结构为LSTM神经网络层，通过循环方法设定不同Cell个数训练神经网络。设置Cell层使用Elu激活函数，隐层神经网络2结构为深度神经网络，使用Xavier方法，使初始化神经网络权值符合截断正态分布，并设定初始偏置为0.1，并将结果送入输出层中。由输出层输出最终结构并送入损失函数中，通过Adam算法对梯度流进行反向计算并更新。神经网络结构算法如下所示。

输入：训练集数据train_X,train_y，序列长度，学习速率，批量训练组数

输出：训练模型

步骤：（1）for(训练轮数=0，训练轮数＜=20000，训练轮数=训练轮数+1){

for(迭代=0，迭代＜批量训练组数，迭代=迭代+1){

2.1.2 准确度试验 在未知土壤样品中分别加入一定量的锌、铜和铬标准溶液，进行加标回收试验来验证方法的准确度。经测定，该方法锌的回收率在98.0%～109.0%，铜的回收率在 92.0%～103.0%，铬的回收率在95.0%～107.2%，准确度可以满足试验要求。

（2）#输入层神经网络

X_drop=Dropout(train_X)；

（3）#隐层神经网络1

Cell=LSTMCell(神经元个数)；

Cell=Dropout(Cell)；

Output1=LSTM算法(Cell,X_drop,激活函数=ELU)

（4）#隐层神经网络2

初始化权值W；

Output2=Output1×W+B；

（5）#输出层

y_pred=更新Output2维度为[-1，序列长度，

输出长度]

（6）损失值=损失函数(train_Y，y_pred)；

（7）Adam(学习速率)最小化损失值；

}；

}；

5 短波天波电路模型评估

5.1 模型评估方案

模型评估指标应具有代表性、客观性与科学性。是对不同参数的神经网络对短波天波电路的规律分析结果与预测结果进行分析判断，最终得出最优模型的过程。应以短波天波电路的变化规律分析主要是根据计算不同模型相对最低点误差之间的间隔进行分析，若为等比例间隔则表明短波天波电路时间变化规律与序列间隔时间成整数倍关系。在判断短波天波电路规律后，针对功率预测的最优模型评估主要有以下三个标准：

1）模型的训练集误差与测试集误差相对较低。

2）模型的预测结果可以大致反映未来一段时间内短波天波电路的变化趋势。

3）不同模型在前两条条件大致相同的情况下，将选择训练时间代价小的模型作为最优模型。

根据模型的评估方法将确定最优短波电路模型，并同短波预测软件进行对比，得出多层神经网络短波电路模型的优劣之处。

5.2 模型评估

5.2.1 9.75MHz电路评估

9750MHz为日本NHK广播电台信号，台站位于日本东京市。数据收集了台站5月21日至5月25日1900～2300接收机接收信号强度，接收规律为30s，接收数据2408条。对数据进行等间隔抽样处理，间隔为180s，得到数据401条。数据预处理后如图2所示。

图2 9.75MHz接收信号强度预处理

将数据划分为训练集和测试集后送入神经网络中。设定信号的序列长度为5、10、15、20与25，则对应接收信号序列为 15min、30min、45min、60min与75min。设定LSTM Cell个数为2、5、10与20。为便于数据展示对不同模型进行编号。损失函数为平方和误差函数则不同模型对应的测试集误差，如表1～2所示。

表1 训练集误差

多次重复实验结果表明，模型具有良好的收敛效果，且能反映出短波天波电路变化趋势，图2表示了5月23日1900～2300短波天波电路的实测值，短波预报软件的预报值与神经网络模型的预测值。其中横坐标为数据采样点，纵坐标为正则化处理后的功率值。经对比发现，神经网络模型的预测结果相较于短波预测软件结果更加贴近实测数据的变化情况，且相对误差较小，预测精度高于短波预报软件。

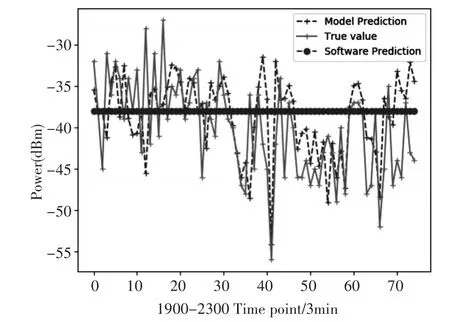
图3 软件预测，神经网络预测与真实值比较

图3 所反映的测试结果是训练集数据为5月21日至5月22日的实测数据。若使用5月21日至5月23日实测数据预测5月24日，经过模型测试误差有所上升，故得知9.75MHz短波天波电路的日变化规律大约为3天。

5.2.2 6.03MHz电路评估

6.03 MHz为中国国际广播电视台一台，台站位于北京。数据收集了台站6月1日至6月3日0900-1000接收机接收信号强度，接收规律为3分钟，接收数据119条。经数据预处理后如图4所示。

图4 9.75MHz接收信号强度预处理

将数据划分为训练集和测试集后送入神经网络中。设定信号的序列长度为5、10、15、20与25，则对应接收信号序列为 15min、30min、45min、60min与75min。设定LSTM Cell个数为2、5、10与20。为便于数据展示对不同模型进行编号。损失函数为平方和误差函数则不同模型对应的测试集误差，如表3所示。

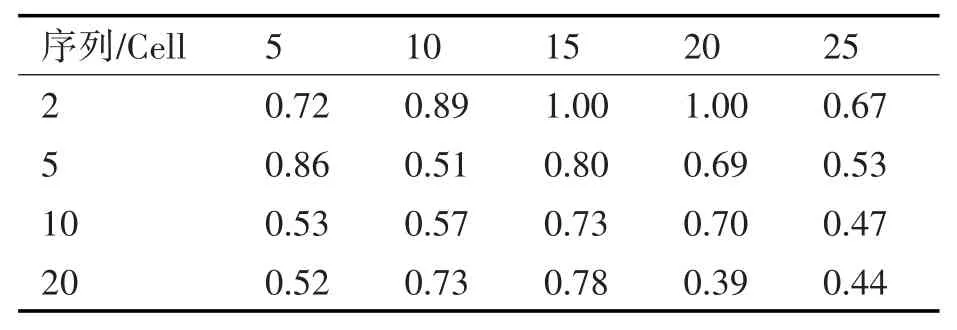
表3 训练集误差

表4 测试集误差

多次重复实验结果表明，模型具有良好的收敛效果，且能反映出短波天波电路变化趋势，适合6.03MHz电路模型。图4表示了6月2日0900-1000短波天波电路的真实值，短波预报软件的预报值与神经网络模型的预测值。其中横坐标为数据采样点，纵坐标为正则化处理后的功率值。经对比发现，神经网络模型的预测结果相较于短波预测软件结果更加贴近实测数据的变化情况，且相对误差较小，预测精度远高于短波预报软件。

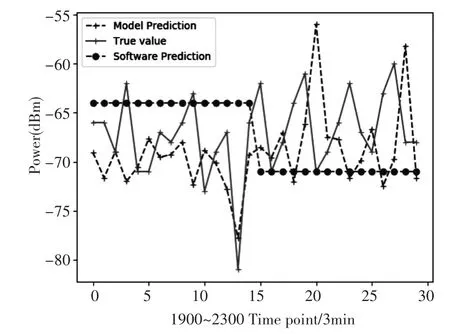
图5 软件预测，神经网络预测与真实值比较

图5 所反映的测试结果是训练集数据为6月1日实测数据。若使用6月1日至6月2日实测数据预测6月3日，经过模型测试误差有所上升，故得知6.03MHz短波天波电路的日变化规律大约为2天。

6 结语

本文讨论了时间因素对短波天波通信电路质量的影响，结合神经网络原理与算法，构建了拟合短波天波电路通信的模型。采集了短波天波电路在不同距离、不同方向与不同距离的通信数据。将采集的数据送入优化后的多层神经网络进行运算，调整神经网络参数，最终拟合出适用于不同短波天波通信电路的模型，分析得到了电路时序的日变化与分钟变化的规律性，并对其进行预测，并同实测值与现有短波预测软件预测结果进行比较，证明模型在预测的精度上高于现有短波预测软件，并验证了多层神经网络可用于短波天波电路建模中。

其中重点完成了使用该短波天波电路下的最优参数神经网络模型，根据不同天数的采集数据重新划分训练集与测试集，调整训练集与测试集比例，分析电路的天变化规律，并将预测结果同现有短波预测软件与测试集数据相比较，分析电路模型的优劣。

在本文中也存在一些不足：1）实验过程中模拟通信过程不能完全模拟正常通信，无法对通信的时间段，通信方式以及发方功率进行调整；2）通信数据数量不足；3）固定参数模型容易受到其他无关变量的影响。