新课标下初高中数学衔接问题

侯向艳

摘 要：课程改革以来，初高中数学教材的衔接问题日益突出，作为一线的高中数学教师感受颇深。初高中衔接问题是一项非常重要的问题，初高中衔接问题处理好，会对整个高中数学教学产生深远的影响。本文就初高中数学衔接问题提出了一些方法和实例，从而寻求解决对策。

关键词：初高中数学;衔接问题;新课标

【中图分类号】G【文献标识码】B【文章编号】1008-1216（2019）10B-0062-02

近些年来，数学新课程改革在中学教育中全面展开，但是随之也产生了一些问题，例如初高中衔接问题日益明显，给当前的数学教学带来了困难。

因此很多一线教师非常关注这个问题，也在积极地寻找方法解决这一问题。本文将结合高中教学的实际提出一些解决初高中衔接问题的方法，从而达到提高高中生数学学习能力的目的。

一、 造成高一学生学习困难的原因

就教材而言，高中数学较初中数学在内容上有了大幅度的调整，难度、深度、广度大大提高，高一数学内容在整个高中阶段经常用到，从集合开始就和初中内容有着紧密的联系，例如一次函数、反比例函数、二次函数的图象，一元二次方程的解法，初中阶段介绍了它们的简单知识，高中阶段则要求熟练掌握和应用。初中数学把韦达定理、十字相乘法都删除了，而在高中阶段却经常出现。初中数学没有介绍一元二次不等式的解法，而高中必修一第一章《集合》就涉及了不等式的解法。初中数学没有介绍平行线分线段成比例定理，而在高中数学中经常涉及。从而导致高中数学教学中学生感到这些知识特别的陌生，造成了学生学习的困难。导致很多老师不得不对这些知识进行补习，占用了很多的课上时间。

就教法而言，初中生学习的自觉性不高，学习目的不明确，需要教师讲得细、讲得多;而高中生的自学能力有一定的提高，课堂教学注重逻辑推理能力的判断和思维能力的培养，通过较少的典型题目的教学从而达到融会贯通。

就学习方法和学习态度而言，初中生注重套用模式，较机械、死板，对知识的整体认识和把握不够，而高中生注重数学方法和思想的培养，不仅要掌握知识还要掌握知识的由来，考查的是学生自主学习的能力。

二、 解决初高中衔接问题的方法

（一）紧扣教材，实现平稳过渡

大多数初中教师和学生学习的目的是应付中考，导致对很多与高中有联系但是中考不考的数学知识一带而过，如十字相乘法。在教学过程中，我发现仅有部分学生会用，有的学生对于二次项系数为1就无从下手，而有的同学甚至没有听说过这个知识点，虽然也可以用配方法、公式法来解答，但是对于有些题目十字相乘法有其独有的优点。

实例1.已知集合，集合，求，。

解：

Θ6x2-11x-30<0

∴（2x+3）（3x-10）<0

∴

∴

同理

Θ7x2-13x-60 =（x-4）（7x-16）<0

∴

∴

综上，，

。

在教学此题时，很多的学生用公式法来解答，然而大部分学生的答案是错误的，显然上述解答过程中十字相乘法很简洁明了。

实例2. 韦达定理（根与系数的关系）一元二次方程ax2+bx+c=0（a≠0）的两根分别为x1，x2，则有x1+x2=， x1·x2 =  。

必修四第三章《三角恒等变换》中有道题目，已知tanα，tan是方程2x2+3x-7=0的两个实数根，求的值。

解：由韦达定理tanα+tan=-，tanα·tan=-

所以，tan（α+）==-。

必修四第三章《三角恒等变换》中同样有这样一道题目，在△ABC中，已知tanA，tanB是x的方程x2+ρ（x+1）+1=0的两个实根，求∠C。

解：由韦达定理tanA+tanB=-ρ，tanA·tanB=1，

所以，tan（A+B）==-，即tan（A+B）不存在，A+B=90°，

所以∠C=90°。

这两个题目都是简单的题目，利用两角和的正切以及韦达定理很容易就解决了。

但是实际情况是，很多学生展开两角和的正切值后却不知道该如何处理。

实例3. 已知函数f （x）=x2-2x-3，

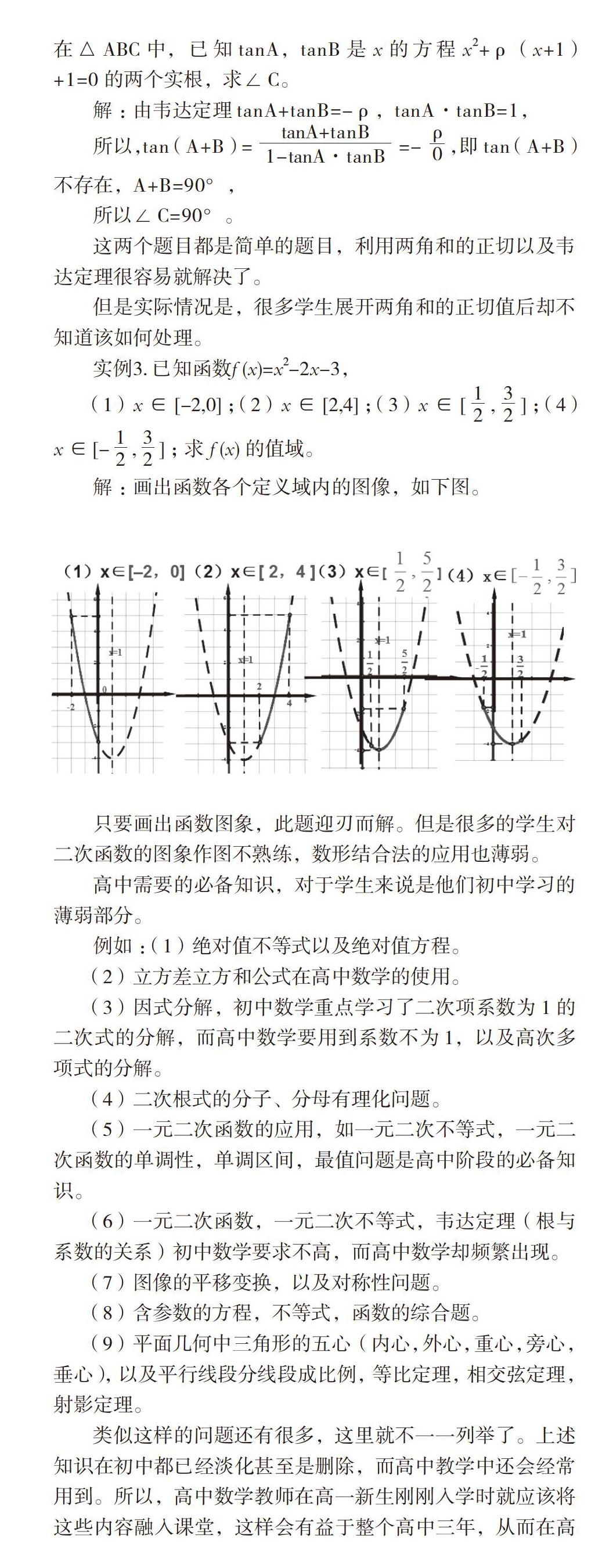
（1）x∈[-2，0];（2）x∈[2，4];（3）x∈[，];（4）x∈[-，];求f （x）的值域。

解：画出函数各个定义域内的图像，如下图。

只要画出函数图象，此题迎刃而解。但是很多的学生对二次函数的图象作图不熟练，数形结合法的应用也薄弱。

高中需要的必备知识，对于学生来说是他们初中学习的薄弱部分。

例如：（1）绝对值不等式以及绝对值方程。

（2）立方差立方和公式在高中数学的使用。

（3）因式分解，初中数学重点学习了二次项系数为1的二次式的分解，而高中数学要用到系数不为1，以及高次多项式的分解。

（4）二次根式的分子、分母有理化问题。

（5）一元二次函数的应用，如一元二次不等式，一元二次函数的单调性，单调区间，最值问题是高中阶段的必备知识。

（6）一元二次函数，一元二次不等式，韦达定理（根与系数的关系）初中数学要求不高，而高中数学却频繁出现。

（7）图像的平移变换，以及对称性问题。

（8）含参数的方程，不等式，函数的综合题。

（9）平面几何中三角形的五心（内心，外心，重心，旁心，垂心），以及平行线段分线段成比例，等比定理，相交弦定理，射影定理。

類似这样的问题还有很多，这里就不一一列举了。上述知识在初中都已经淡化甚至是删除，而高中教学中还会经常用到。所以，高中数学教师在高一新生刚刚入学时就应该将这些内容融入课堂，这样会有益于整个高中三年，从而在高考中取得好成绩。

（二）加强学习方法的指导

教会学生如何预习、如何听课，培养学生的自学能力，以及独立思考能力。如，作业反馈，试卷分析，与学生定期、不定期地交流，同学间互相学习，扬长避短。举办一些活动如学习方法讲座。培养学生养成良好的学习习惯，提前预习效率，高中数学的特点难度大，内容多，通过提前预习可大大提高学生上课的学习效率，从而解决目前老师满堂灌、学生满堂学的实际问题。教会学生及时地归纳总结，细化到每节课、每次作业、每次考试。

（三）认真学习《普通高中数学课程标准》，提高教育教学质量

认真学习《普通高中数学课程标准》，不要随意调整和增加内容，如必修四第一章《三角函数》、第二章《平面向量》、第三章《三角恒等变换》，有很多教师把第一章和第三章调整到一起教学。第一章已经有很多公式，再加上第三章的公式，学生记忆困难，学习困难。与此同时，《三角恒等变换》这章的第一个公式cos（α-）=cosαcos+sinαsin）的证明用到第二章《平面向量》的知识，导致知识不连贯。第三章《三角恒等变换》比较灵活，很多老师补充很多的公式增加了学生记忆负担，從而导致学生学习效果不是很好。

在学生信心满满地跨入高中校园时，他们都对高中数学充满兴趣、充满信心，然而他们往往要经历各种挫折和困难。我们要分析产生挫折的原因，帮助学生正确地克服和面对困难，做好初高中的衔接，从而能够更好地开展高中数学的教学，提高高中数学的教育教学质量。

参考文献：

[1]李平，赵学焜.浅谈如何做好初、高中数学衔接问题[J].高中数理化（高一版），2006，（5）.

[2]黄鹭芳.积极应对，搞好初高中数学教学的衔接工作[J].福建教育学院学报，2006，（3）.

[3]郑玲薇.新课程背景下初高中数学衔接的实践反思[J].数学学习与研究（教研版），2008，（10）.

[4]娄爱林.搞好初高中数学的衔接，减少掉队人数[J].中国科教创新导刊，2008，（8）.

[5]王艳.初高中数学教学衔接问题研究[D].四川师范大学，2012.

[6]郝娟.新课程背景下初高中数学教学衔接问题的研究与实践[D]. 陕西师范大学，2010.

[7]马晓丹.浅谈初高中数学的衔接教育问题[J].文化创新比较研究，2017，（2）.

[8]钟伟连.谈初高中数学教学过渡问题与对策[J].中国校外教育，2017，（26）.

[9]刘桥连.基于数学核心素养的初高中数学衔接教学策略探究[J].西部素质教育，2017，（19）.

[10]秦红霞.初、高中数学过渡期的教学研究[J].亚太教育，2016，（2）.

[11]李博.初高中数学衔接中的问题分析与对策[J].亚太教育，2016，（5）.