基于多模型PF的风力机桨距系统的故障诊断*
2019-12-24王进花
曹 洁, 任 倩, 王进花
(1.兰州理工大学 计算机与通信学院,甘肃 兰州 730050;2.兰州理工大学 电气工程与信息工程学院,甘肃 兰州 730050)
0 引 言
随着风力机装机总量不断增加,系统结构日益复杂,不同部件之间耦合更加紧密,一个微小的故障可能传播成灾难性的大故障,引起风力机停机,甚至直接导致机组损坏,这不仅浪费了大量风能,增加了维修成本,一定程度上还缩短了风机的运行寿命。风力机桨距系统是风力机运行非常重要的一部分,同时也是风力机故障的高发部位[1,2]。因此对风力机桨距系统一些潜在的故障进行检测与分离是至关重要的。
桨距系统的故障诊断方法主要分为基于数据的故障诊断和基于模型的故障诊断。基于数据驱动的故障诊断需要大量的离线历史数据,这些数据不能反映系统当前的变化情况,具有工作量大且实时性差的问题[3~5]。
基于模型的故障诊断方法通过系统的结构、行为和功能等方面的知识对系统进行诊断推理,无需先验知识,对故障数据的依赖性较小[6]。文献[7]通过建立风力机桨距系统动态模型,利用基于模型的方法对桨距系统进行故障检测。文献[8]提出了一种基于观测器的多新息随机梯度辨识算法的故障诊断方法,实现了桨距系统的故障检测。文献[9]通过带扰动补偿器的离散时间控制器对桨距系统进行故障检测与容错控制,有效地检测出了桨距系统执行器的故障。文献[10]采用区间预测方法诊断风力机桨距执行器故障,提高了故障诊断的鲁棒性。文献[7~10]均实现了桨距系统的故障检测,但在实际应用中,系统存在的各类信号扰动和随机噪声,会对故障诊断准确性的产生影响,以上文献均没有对其作详细的研究。
因此,本文针对各类信号扰动和随机噪声导致的故障诊断不准确的问题,在桨距系统的多故障模型的基础上,采用粒子滤波对其进行状态估计;设计并优化自适应阈值,提高故障检测的准确率同时减少计算时间,引入J散度改进基于多模型的故障分离方法,提高故障分离的准确性。
1 风力机桨距系统故障模型
1.1 桨距系统执行器数学模型
本文针对桨距角执行器故障问题进行研究,风力机桨距系统由3个完全一致的桨距执行器组成,桨距执行器通过旋转叶片控制桨距角的大小。桨距执行器可以建模为桨距角β(t)和桨距角参考值βref(t)之间的传递函数。β(t)是桨距系统的输出,βref(t)是风力机控制器给出的设定值。桨距执行器的二阶传递函数模型如下[11]
(1)
式中ωn为桨距系统的自然频率,ζ为桨距系统的阻尼系数。
1.2 桨距系统执行器故障模型
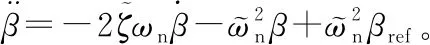

表1 桨距系统故障特征参数表
2 多模型粒子滤波的故障诊断
2.1 粒子滤波算法
假设k时刻非线性系统的状态值是xk,量测值是zk,则非线性系统的动态空间模型可表示为[12]:状态模型xk=fk(xk-1,uk-1);量测模型zk=hk(xk,vk)。其中,fk(·)为系统状态转移函数,hk(·)为系统观测函数,uk-1与vk分别是非线性系统的过程噪声和量测噪声,且两者互不相关。
标准粒子滤波算法是通过前一时刻的状态值和当前时刻的量测值来递推估计当前时刻状态值的过程,其重要性密度函数选取的是先验概率密度p(x0),并引入重采样技术来缓解粒子退化问题。标准粒子滤波算法主要由初始化、粒子预测、权值计算、状态更新、重采样组成,其具体的实现步骤如下:
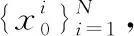
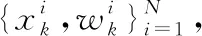
(2)
从而得到近似后验概率密度为
(3)
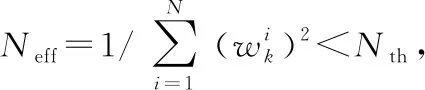
5)判断是否结束:若结束,则退出该算法,反之转到(2)。
2.2 多模型粒子滤波的故障诊断
假设一个非线性系统可以用如下描述
Σm:xk=f(xk-1,uk-1),yk=h(xk)
(4)
式中x∈Rnx为系统状态向量,y∈Rny为系统观测向量,u∈Rnu为控制向量。
假设存在有限个已知的模型Σi(i=1,2,…r)
(5)
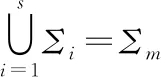
称式(5)为式(4)的多模型描述,Σs为子模型族,Σi(i=1,2,…r)为子模型。
假设系统存在n个已知的故障模型,各种故障模型为
(6)
正常模型为
(7)
式中m=1,2,…,n为各种故障模型。则需要设计n+1个粒子滤波器,每个粒子滤波器独立监控一种状态。
3 桨距系统故障诊断
3.1 故障诊断算法原理
构建系统的状态空间模型如下
20世纪50年代末,美国语言学家约瑟夫·H·格林伯格打开了语言学研究的一个新的领域——语言类型学。该理论主要的观点是在对人类语言的机制和规则进行概括总结时,必须要进行跨语言验证,而要研究任何一种语言的特点都离不开跨语言比较出的共性和类型分类的基础。我国著名英语学者许国璋也提出:“过去的研究太过于强调汉语和欧洲语言之间的差异,而忽视了两者之间的相同点。”[1]近年来,语言类型学逐渐风靡,挖掘汉语和英语之间的共性和差异,掌握两者之间的普遍特征成为潮流。
xk+1=Axk+Buk+ωk,yk=Cxk+vk
(8)
状态量为x=[βωrωgθΔ]T,控制量为u=[TrTgβref]T,y为桨距角,A,B,C为已知的系统矩阵,ωk和vk分别为系统噪声与观测噪声,且两者互不相关。
根据风力机桨距系统的故障描述,及式(13)、式(14)多模型粒子滤波的设计可得到以下故障诊断原理图,如图1。
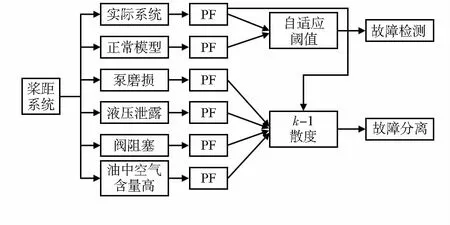
图1 桨距系统多模型故障诊断算法原理框图
3.2 自适应阈值的设计
在系统多故障模型的基础上,将理想观测值和实际系统状态的观测值产生的差值作为残差,残差是判断故障是否发生的依据,针对传统故障检测方法中故障误报率高,实时性差的问题,本文引入统计学中置信区间的思想设计一个随着残差变化的自适应阈值[13],k时刻的残差大于阈值,则说明系统发生了故障。假设残差的统计特性符合正态分布,则残差的均值和方差为
(9)
(10)
式中η(uj,tk)为输入为uj时tk时刻残差的均值。δ2(uj,tk)为输入为uj时tk时刻残差的方差。
引入统计学中置信区间运用于设计自适应阈值,但这种方法计算自适应阈值,为了得到当前时刻残差的均值和方差,在算法迭代的每一步都需要系统重复运行n次,计算量近似指数增长,很难满足实际系统的实时性要求。本文受文献[14]启发,引入一个经过多次实验得到的带宽系数来优化自适应阈值的均值和方差,使得均值和方差的计算只依赖上一时刻的值,从而达到在保证故障检测准确率的同时提高实时性。
自适应阈值定义为
rth,k=η(uj,tk)±2.17δ(uj,tk)
(11)
第N时刻残差的均值和方差表示为
(12)
(13)
(14)
(15)
3.3 故障分离
传统的故障分离方法受信号干扰、噪声影响较大,不能充分地利用故障特征;J散度与多模型结合的故障分离方法可以充分提取粒子滤波估计后的非高斯故障特征,在系统建模不精确的情况下提高故障分离的准确性。
1)J散度
假设一维随机变量为存在两种可能的概率密度函数p1(ζ)和p2(ζ),则p1(ζ)对p2(ζ)的信息散度为[15]
(16)
为了克服其不对称性,提出了J散度
DJ(p1(ζ),p2(ζ))=
(17)
2)基于J散度的故障分离
首先通过核密度估计公式计算故障模型输出和实际系统模型输出的概率密度函数,再通过J散度计算两个输出的散度大小,散度越小则为同一故障的可能性越大。
假设ζ1,ζ2,…,ζ为实际系统输出ζ的一组统计数据,则其概率密度函数ζ的核密度估计为
(18)
假设θ1,θ2,…,θ为故障模型输出θ的一组统计数据,则其概率密度函数p(θ)的核密度估计为
(19)
实际系统输出与故障模型输出的J散度
D(p1(ζ),p2(θ)=
(20)
算法流程如图2。
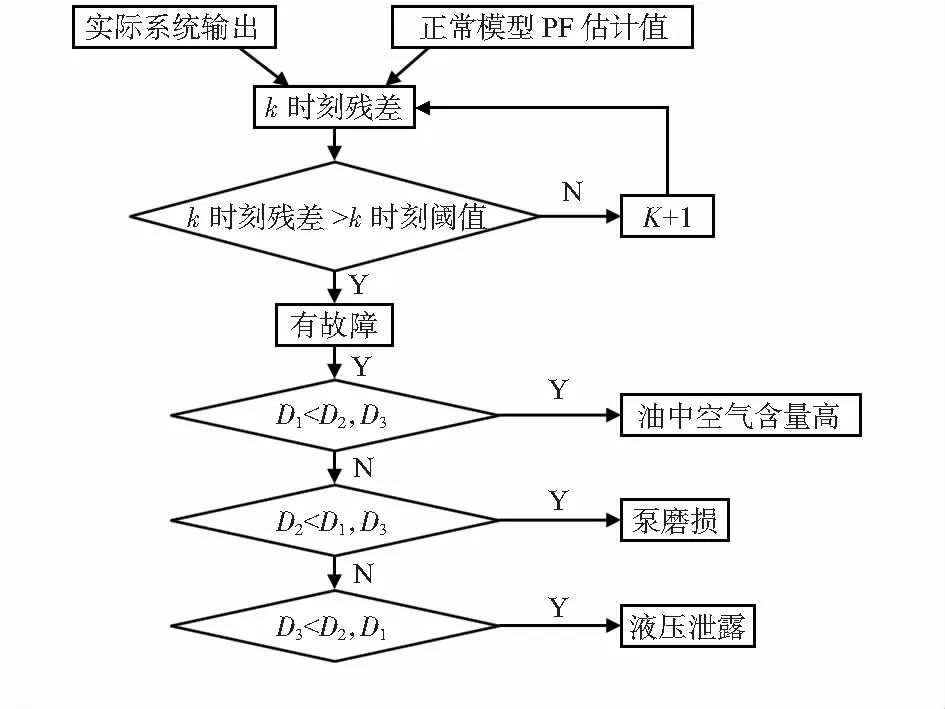
图2 故障诊断算法流程框图
4 仿真分析
采用4.8 MW级风力发电系统实际参数,通过改变实际风力机的故障特征参数模拟风力机桨距系统的三种故障,利用MATLAB平台,设置初始状态x=[0.404 63 162 5.6 0.504]T,输入为u=[5.915 4×107500 4.5]T,采样粒子数N=200,仿真时间T=200 s,离散步长ΔT=0.01 s。考虑系统中存在未知噪声等干扰的影响,采用滑动窗M,M=20。本文设置噪声形式为ω~Γ(0.1,0.1),v~Γ(0.1,0.1)。
故障误报率pf和漏报率pm
式中A为系统实验的总仿真数,C为在A次仿真中系统未发生故障时残差大于阈值的时间点总数,D为一次仿真中系统未发生故障的时间点的总数,E为在A次仿真中系统发生故障时残差小于阈值的时间点总数,F为一次仿真中系统发生故障的时间点总数。
假设故障的出现在120~140 s,故障表示信号为
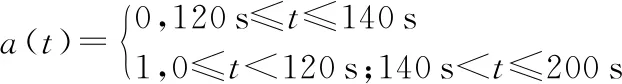
实验一:故障检测。本文引入的自适应阈值检测故障的算法中,置信度为97 %,Z=2.17。
图3为当实际系统依次发生油中空气含量高、泵磨损、液压泄露三种故障时自适应阈值与残差的变化,可以看出,0~120 s和140~200 s时,残差一直处于平稳状态,并且小于自适应阈值,120 s时残差发生突变,120~140 s时残差大于自适应阈值,可见系统在120~140 s发生了故障,因此本文故障检测算法可以有效的实现故障检测。
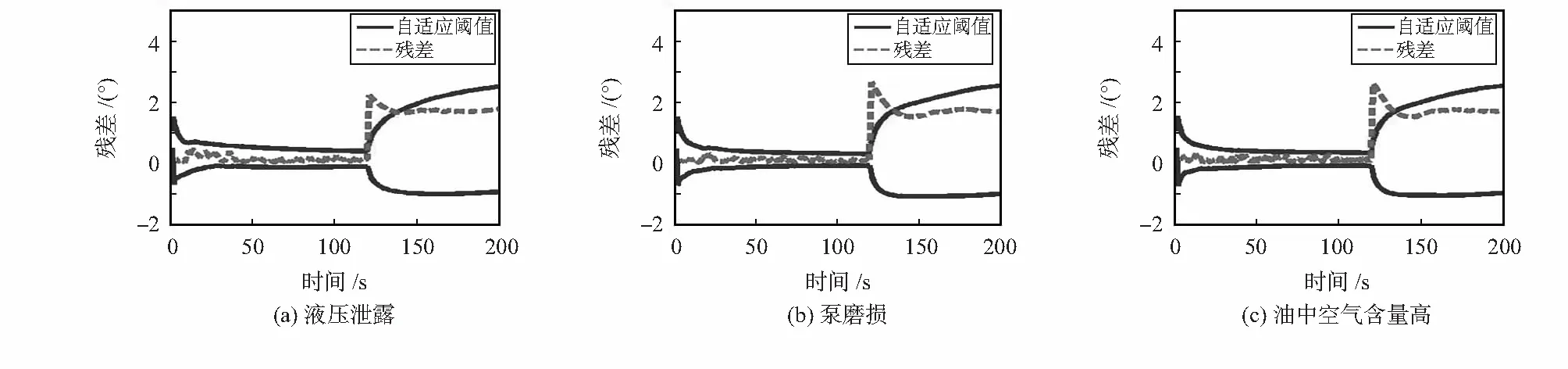
图3 三种故障下的残差与自适应阈值对比
图4为固定阈值法[16]与自适应阈值法的故障检测结果,0代表发生故障,1代表无故障,120~140 s时实线比虚线的检测点数更多,可见自适应阈值检测法的检测结果比残差平滑值检测法更准确。

图4 两种检测算法的检测结果
表2为以上两种检测算法所得结果的漏报率与误报率,实验中系统运行50次,每次运行的采样点数为500,通过对所有采样点在50次运行中出现漏报的采样点数进行统计,并利用漏报率公式计算得到漏报率。明显自适应阈值算法比残差平滑值方法更加准确,故障漏报率和误报率都有了减小。可见本文故障诊断算法相比固定阈值检测法明显提高了准确性。

表2 两种方法的漏报率与误报率
表3为优化前与优化后的自适应阈值检测法的计算时间对比,可以看出优化后的自适应阈值检测法比优化前明显提高了计算效率。并且当粒子数越多,计算时间缩短越明显。由此可见,本文算法提高了故障诊断的实时性。

表3 优化前后的运行时间对比
实验二:故障分离。当实际系统依次发生三种故障时,采用两种不同的分离方法所产生的分离结果如图5、图6。

图5 基于J散度的故障分离结果
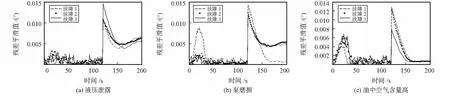
图6 基于残差平滑值的分离结果
图5为基于J散度的故障分离结果,图6为基于残差平滑的故障分离结果[17],如图所示当实际系统发生三种故障时,基于J散度的分离方法可以清晰的看出,发生第i类故障的Di最接近0,由此可以判断出此时系统发生的故障类型为第i类。而基于残差平滑值的方法每一时刻大小不一致,很难判断看出哪个更接近0,它受系统噪声与信号干扰的影响较大。以上可见本文方法能够更加准确地分离出故障。
5 结 论
风力机桨距系统是个非线性、强耦合的系统,存在各种噪声、信号干扰,从而导致建模不精确,本文在桨距系统多故障模型的基础上,采用粒子滤波算法对其进行状态估计,得到每个模型的输出,引入自适应阈值,利用经过多次实验得到的带宽系数优化自适应阈值,实现了故障准确检测的同时减少了计算时间,提出J散度与多模型相结合的分离方法,允许建模误差的情况下实现了故障的准确分离,仿真结果验证了本文故障诊断算法的可行性和有效性。
