BP神经网络在爆破振动中的研究与应用

2019-12-24冷智高李祥龙宋春辉陶子豪

有色金属（矿山部分） 2019年6期

冷智高，李祥龙，程明，宋春辉，陶子豪

(昆明理工大学国土资源工程学院，昆明650093)

岩体爆破是一个极为复杂的过程，它是多因素与多目标之间的复杂关系，存在很多难以用数理进行统计的影响参数，目前尚没有一个完全理论化的公式可以对爆破效果进行公式计算，很多情况下工程师都是通过半经验半公式以及类比方法对爆破效果进行预测计算。目前而言应用较多的是萨道夫斯基经验公式，但萨氏公式仅考虑装药量和爆源距两个因素[1]，无法充分的考虑影响爆破结果的因素，故而预测误差较大，难以进行爆破预测。随着行业标准的提高，人们对安全意识的加深，施工方对爆破效果的要求也越来越高，这就要求使用更加精确的预测公式或模型提高爆破效果的预测精度。

近几十年来，随着人工神经网络的发展，为人们解决了现实中大量的非线性问题，它在进行模糊控制、不确定控制中具有独特的优势[2]。爆破工作者们也逐步将这项技术应用到爆破效果的预测中来，取得了非常满意的效果。韩亮等[3]结合Weibull模型和BP神经网络对高台阶抛掷爆破爆堆形态进行研究；王建国等[4]利用神经网络研究露天煤矿爆破振动；徐全军等[5]利用神经网络预测爆破地震峰值；林从谋等[6]也利用神经网络研究隧道掘进爆破地震的峰值。人工神经网络模型中应用最为广泛[7]也最为成熟的就是BP神经网络模型。

1 BP人工神经网络

1.1 BP人工神经网络原理

人工神经网络(Artificial Neural Network，ANN)是非线性程度相当高的动力系统，具有极强的非线性动态处理能力。人工神经网络方法不需要事先假设数据或变量之间的服从规律或内在联系，而是直接通过网络之间的权值训练，找出输入与输出变量之间的非线形关系[1]。BP人工神经网络(Back Propagation Artificial Neural Network)是具有反向传播功能的前馈网络(Feedforward Network)，是一种建立在梯度下降法基础上的自学算法，它利用输出后的误差来估计输出层的直接前导层误差，再利用这个误差更新前一层的误差。如此一层一层的反传下去就获得了所有其他各层的误差。

BP网络属于多层次的人工神经网络[8]，BP神经网络结构由输入层(LA)、输出层(LB)和隐含层(LC)构成，各个神经层内由大量只能处理简单信息的神经元构成，而构成的结构则可以模拟人的大脑对非线性问题进行处理，神经层之间通过权值(w)和阈值(θ)进行连接，每层神经元之间无连接。BP神经网络的拓扑结构[9]如图1所示。

图1 BP神经网络拓扑结构Fig.1 Topological structure of BP neural network

BP神经网络通过外界输出样本的刺激不断改变网络的连接权值，为使网络输出不断地接近期望输出，一般称为神经网络的学习或训练。其本质是对各层神经间的连接权值进行动态调整。

BP人工神经网络具有良好的自学习、自适应、联想记忆、并行处理和非线性转换的能力,避免了复杂数学推导，在样本缺损和参数漂移的情况下,仍能保证稳定的输出[10]。

1.2 BP神经网络理论计算

设有N1个输入样本，即输入层神经元个数为N1个初始权值(w)和阈值(θ)，一般把权值和阀值设置成较小的随机数[11]，隐含层神经元个数为N2，输出层神经元个数为N3，其激活函数均为Sigmoid函数，见式(1)[2,12-14]。

(1)

神经网络节点i的输出见式(2)。

Ii=∑kWikOk

(2)

式中，Wik—神经节点i和k之间的连接权；Ok—节点k处的输出值，Ok=f(Ii)。

使神经网络输出Qk与第p个期望输入Ep之间的差满足式(3)、式(4)。

(3)

(4)

式中：Ek—第p个样本训练得到的输出误差和；E—n个样本完成一个训练周期后得到的累计误差；ε—误差限。

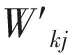
(5)

式中：η—学习速率；Ek—第k个神经元的期望输出。

(6)

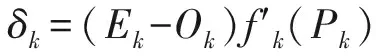
2 BP神经网络模型的建立

2.1 输入层个数的确定

BP神经网络模型的输入层一般是影响结果的参数，就爆破工程而言输入层参数即为爆破影响因素，不同学者考虑的因素有所不同，故而个数也不尽相同，例如张成良等[15]将岩体强度、岩体的裂隙发育程度、炮孔直径、孔深作为输入层参数；祝文化等[16]将岩体条件、岩石特性、开采工艺参数、爆破网络几何参数、炸药特性等17个因素作为输入层；林从谋等[17]将孔深、孔数、孔距、最大齐爆药量、总药量和爆源距设为输入层参数；张艺锋等[18]将总药量、单段最大药量、爆破段数、爆心距、场地条件特征作为输入层参数。

影响爆破效果的因素按其性质可划分为[19]岩体条件、岩石特性、开采工艺参数、爆破网络几何参数、炸药特性，但是不同的影响因素对爆破结果的影响程度不同，有的程度大有的则相反。若将如此多的影响因素全部作为输入层神经元，不仅不会使预测结果精度得到有效地提高，反而会使神经网络的结构更加复杂，增加网络的运算步数，降低运算效率。所以确定某个输入层参数还需要考虑该参数对爆破结果的影响程度，若某些参数影响较小则可直接删除不予考虑。

2.2 隐含层神经元个数的确定

据Kolmogorov 3层神经网络映射存在的定理，隐含层神经元个数与输入层神经元个数之间遵循N2=2N1+1，即隐含层神经元个数等于输入层个数的两倍还多一个。不同学者设定的不同的输入层参数个数会出现不同隐含层个数的结构。

2.3 输出层神经元个数的确定以及网络模型的学习训练

BP神经网络模型的输出层参数即为爆破工作者所预测的结果或爆破效果，除本文引言部分应用外还有祝文化等[16]应用BP神经网络模型预测爆破块度，言志信等[20]预测爆破振动峰值。

BP神经网络模型是具有学习联想性、鲁棒性和高度容错性，能够处理高非线性问题的网络模型，它不需要提前设定好，只需将符合工程需要的爆破结果数据作为学习样本训练根据式(5)、(6)逐渐调整各层之间连接的权值和阈值，使得训练结果的误差符合期望误差，即学习训练结束，调整后的连接权值和阈值便可用于模型预测，再将需要预测的爆破参数输入到训练好的神经网络中便可预测结果。

作为模型训练样本数据指标不同，且样本中各向量的数量级差别很大。为计算方便和防止部分神经元达到过饱和状态[21]，需要对训练样本数据按式(7)作归一化处理。

(7)

而预测后的结果是经过归一化处理的，为使数据更加直观需对预测后结果进行反归一化处理，即按式(8)处理。

x=x′[max(x)-min(x)]+min(x)

(8)

经归一化后的训练样本训练的模型最后具有N1-N2-N3的拓扑结构(Topological Structure)。

2.4 工程爆破中BP神经网络模型的应用

BP神经网络模型在处理非线性问题方面的优良性质，让越来越多的国内外学者将其应用到爆破研的究领域，除前文所述学者研究成果外，M·MONJEZI等[22]将BP神经网络应用到预测爆破产生的飞石，并优化爆破相关参数对飞石距离进行控制以减少其对人员设备的损伤；赵国彦等[23]将POS算法应用到BP神经网络用来优化爆破大块率相关参数。

李洪超等[24]应用BP神经网络模型预测布沼坝露天矿爆破效果，发现该网络模型能够很准确的对爆破结果进行预测；特种爆破中应用BP神经网络对方案进行评估也能取得很好的效果，田成祥等[25]建立了评估工程兵桥梁爆破方案的BP神经网络模型，验证了模型良好的应用性质；周强[26]在其硕士学问论文中基于BP神经网络在求解不确定问题的优越性，建立了BP神经网络评价模型评价拆除爆破安全性；在高含水岩层中，李玉能等[27]基于BP神经网络对爆破振动参数进行预报，发现预报结果与实测值较为接近；蒲传金等[28]利用BP神经网络模型预测大桥桩基爆破振动，与传统预测公式相比精度提高6～7成；除此之外，还有不少学者[29-30]利用BP神经网络模型对爆破参数进行优化，以期取得更好的爆破效果。

2.5 对BP神经网络模型的修正

BP神经网络对爆破振动的预测误差一般在10%左右，符合现实的工程要求。孙文彬等[31]研究了不同隐含节点个数、训练函数、转移函数、学习率对 BP 神经网络预测结果准确性和收敛速度的影响，最后得出最优的BP拓扑结构为10-6-3，并不符合Kolmogorov定理，最佳训练函数为Levenberg-Marquart(LM)函数，而大多数学者大多使用弹性下降法，最佳转移函数是正切和线性函数，最佳学习率是0.77；苟倩倩等[32]为优化网络结构提高网络的容错性能，建立了PAC-BP神经网络计算模型，预测精度显著提高；文献[14]建立了两个BP神经网络，在模型1的基础上将区域地质条件，岩体RMR值纳入输入层参数建立修正模型2，发现模型2精度比模型1高5%～8%，且两个模型的预测精度与传统的萨道夫斯基公式相比具有较大提高；施建俊等[33]利用Matlab强大的计算能力，结合VB的友好界面开发得到爆破振动峰值预测的系统，该系统预测精度高，人机交互界面友好。