植保机均匀性喷雾的优化控制方法

郑 薇，王向东，李树江，张凯丽

(沈阳工业大学 信息与工程学院，沈阳 110870)

0 引言

传统的喷药方式采用人工式喷药，不仅工作强度大、喷药不均匀，且可能出现重喷、漏喷等情况，无法保证喷雾质量，对环境也会产生一定的污染，使作物产生抗药性，增加作物感染寄生虫的风险，还会造成直接或间接的人体伤害[1-5]。在20世纪中期，植保机已普遍应用于西方农业之中，病虫草害的防治已达到全面机械化。因此，环境友好型可变喷雾技术成为近几年国内研究的热点。

国内外很多学者都曾以环境友好型喷雾为目标对PWM变量喷雾进行研究，却很少有人在关注喷药量的前提下关注过喷雾质量，即喷雾的均匀性。Shaheabadi[6]基于GPS的变量喷雾系统，研究了一种改进的PWM算法，该算法通过改变脉冲的宽度和脉冲的个数来改变流量的调节范围，理论上实现了0～100%的调节范围。Kleber R. Felizardo[7]等人通过对PWM变量喷雾进行研究，可有效地控制喷雾量的变化，实现控制误差在5%以内，大大节约了农药的使用量。F.Lebeau[8]采用PWM变量喷雾技术，沿着喷嘴轨迹使用恒定距离间隔，通过二维喷雾图案与每个位置间隔中花费的时间的卷积来计算喷雾沉积的分布。Elmer A. G. Penaloza[9]利用已开发的计算模型，研究了输出孔口直径和喷雾速度对液滴直径和喷雾锥角的影响。Lu Liu、Feng Chao[10-11]等人对喷雾均匀性的影响进行研究，提高了喷雾的整体质量。蒋焕昱、张利君[12-13]等人采用胭脂红溶液，浓度吸光度技术对喷雾的前进方向、杆方向和总体进行喷雾均匀性的测量，考察了PWM频率、占空比，以及喷雾压力对喷雾均匀性的影响；之后，又在原有基础上进行了改进和优化，采用胭脂红溶液，浓度吸光度技术对单喷嘴进行试验，考察了PWM的频率、占空比和喷雾前进速度对喷雾均匀性的影响，并采用RSM响应面法进行模型的构造、优化和验证。与之前的静态喷雾常规研究相比，此研究可以更准确地评估动态喷雾的实际喷雾分布均匀性。

在此基础上，本文通过对多种影响因素进行分析确定最佳均匀性的取值，并采用线性二次型最优控制算法，实现转速对影响因素的跟踪控制，有效减少喷雾不均造成的农药浪费及土地污染等诸多问题。

1 均匀性分析

1.1 均匀性描述

1992 年，Smith 提出用分布的变异系数cv来确定喷雾分布的均匀性：cv越小表示喷雾的均匀性越好。从农艺角度上来讲，cv值应不超过15%，cv值可以通过以下公式计算，即

(1)

(2)

(3)

式中s—集雾穴盘上孔的沉积浓度的标准偏差；

xi—每个孔中溶液的沉积浓度(μg/cm2)；

通过浓度-吸光度技术，可以计算得出分布的变异系数。

1.2 影响因素

雾量分布是否均匀是衡量喷头性能的重要指标。影响喷雾均匀性的因素[14]有很多，有文献[15]表明均匀性与喷雾的高度、压力及喷头的类型有关，因此试验研究了喷头类型、喷雾压力及喷雾高度对分布变异系数的影响。应用MatLab软件，采用多元线性回归的方法对数据进行分析，利用正交试验设计表中的数据，建立回归模型，即

cv=β0+β1T+β2P+β3H

(4)

式中cv—变异系数；

T—喷头类型；

P—喷雾压力(MPa)；

H—喷雾高度(cm)；

β0,β1,β2,β3— 均为回归系数。

经过MatLab软件对数据的处理，得到回归系数及其检验参数，从而得到回归方程为

cv=60.9778-4.1667T-1.5167P-3.1167H

(5)

相关文献表明：喷雾的均匀性与PWM控制信号的频率、占空比及喷施机组的行进速度相关，其关系为

cv=107.312-1.269T-29.157F+152.721V+

0.142DF-0.473DV-7.37FV+2.315E-

3D2+1.563F2-10.454V2

(6)

式中D—PWM控制信号的占空比(%)；

F—PWM控制信号频率(Hz)；

V—喷施机组行进速度(m/s)。

因此，本文提出推论喷雾的均匀性与喷头类型、喷雾高度、喷雾压力、PWM控制信号频率、占空比，以及喷施机组的行进速度均有关系。

1.3 一般方法

本文采用改进型约翰迪尔4130系列喷雾机，Spray systems Co.,American,H-VV9515型扇形喷头，在保证喷雾量的前提下，以寻求最佳均匀度为目标，即在分布变异系数取最小值时，找到各项因素的最佳取值。采用浓度-吸光度技术，应用响应面法对多种影响因素进行试验分析可知：当喷头间距为50cm、喷雾高度为30cm、泵后喷雾压力为2MPa时，分别给定占空比、频率、喷施机组行进速度一个上下限：20%～60%、5～9Hz、0.5～0.7m/s带入到式(6)中。由于分布变异系数是关于占空比、频率、喷施机组行进速度的线性函数，其导数为常数，所以其最值一定在边界达到，计算后可知当频率为7Hz、车速为0.5m/s、占空比为60%时均匀性最佳，最佳为5.36，小于15，满足工艺生产需求。由于影响因素较多，会增加模型的复杂性和非线性，本文采用占空比和喷雾压力作为被控变量，建立一个喷雾压力系统模型，采用线性二次型最优控制算法通过控制离心泵的转速使孔口喷雾压力和占空比达到最佳均匀性。

2 改进型约翰迪卡尔模型的均匀性研究

2.1 喷雾系统结构图

喷雾系统由药箱、离心泵、过滤器、节流阀、平面扇形喷头及管道等组成，如图1所示。

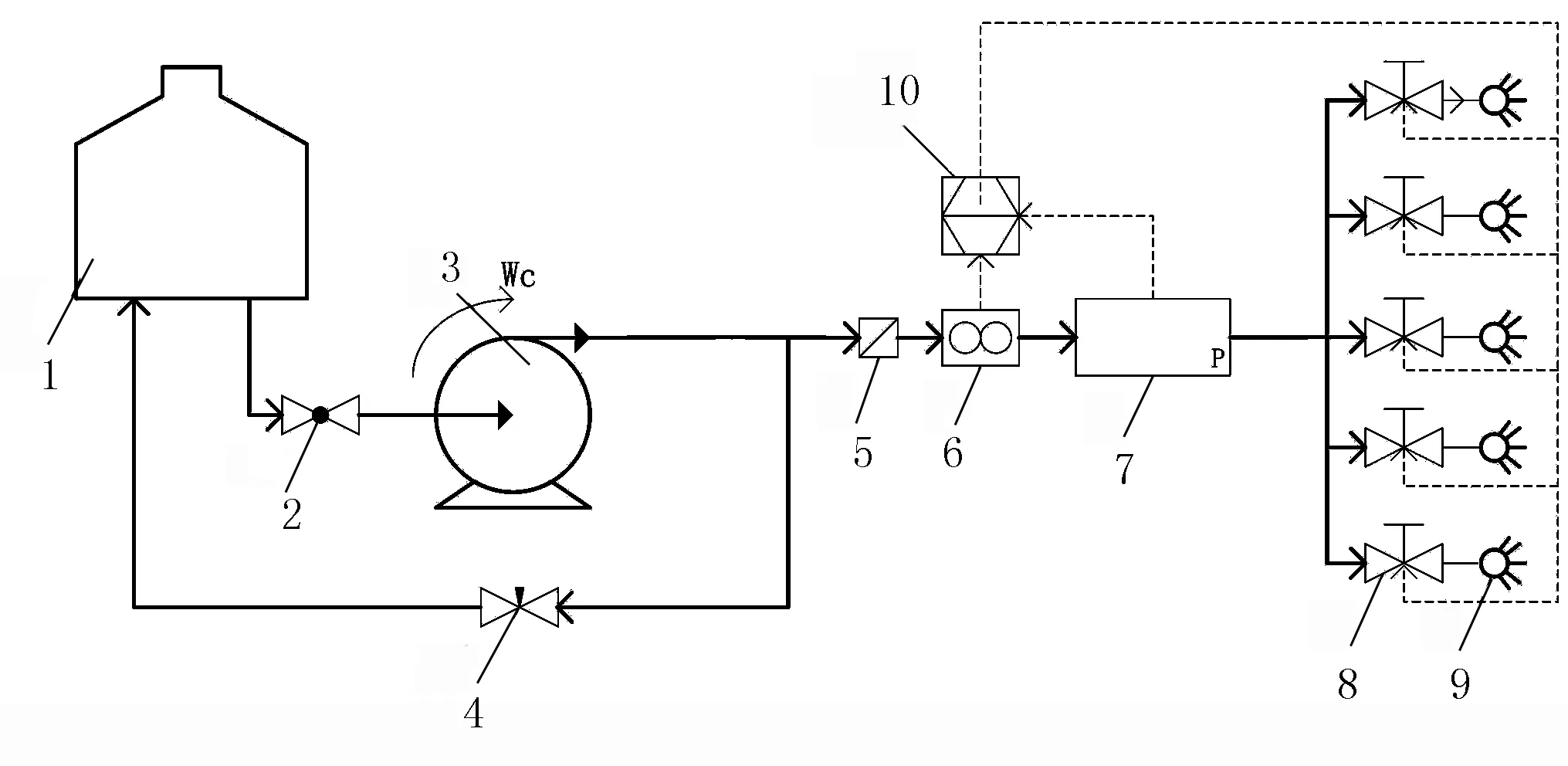
1.药箱 2.吸液阀 3.离心泵 4.搅拌阀 5.过滤器 6.药液流量计 7.压力传感器 8.电磁 9.喷头 10.SRC/CCU控制单元

工作原理：泵启动后，药液通过进液口从药箱中抽出，泵驱使药液一路经过喷杆的供液管、过滤器和流量计到达喷嘴，雾化并喷射，一路到达搅拌流量阀进行搅拌。喷杆供液管上的压力传感器将电信号送至CCU/SRC，由其将接收到的信号与设定的压力值进行对比，如果压力传感器信号与设定的压力值存在偏差，则对离心泵的转速进行调节，直到系统稳定在目标压力值为止。

由图1及其工作原理可知：离心泵转速的变化直接影响流入管道的药液流量，从而引起管道压力的变化，因此本文建立了一个由离心泵和管道系统组成的喷雾压力系统动态模型。

2.2 喷雾压力系统动态模型的建立

2.2.1 离心泵模型

泵的模型描述为

qpr=kpwc

(7)

式中qpr—供应管道流量(L/min)；

kp—泵的容积排量(mL/r)；

wc—泵的转速(r/min)。

由于泵在工作过程中会产生泄露损失，所以泵的实际流量小于理论流量，但其容积效率很高，因此可以在理论估算时忽略不计，即不考虑泵的泄露问题。

2.2.2 管道系统模型

基于药液压力动态模型为

(8)

式中qin—药液流入(L/min)；

qout—药液流出(L/min)；

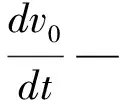
kf为体积弹性模量[16]，一般情况下定义为

(9)

式中dp—药液压力变化量(MPa)；

dv—药液体积变化量(L)；

v—药液初始体积(L)。

由式(9)可知：只要知道药液的初始体积v,压力变化量dp和体积变化量dv就可以计算出药液的等效体积弹性模量[17]，它与时间及给定的压力大小无关，只与对象的性质有关。由此可得管道的药液压力动态模型为

(10)

vr—管道内药液体积(L)；

qpr—供应管道流量(L/min)；

q—管道出口流量(L/min)。

其中，q为实际施药量。

2.2.3 喷雾压力系统模型

结合式(7)、式(10)可得喷雾压力系统模型为

(11)

根据不同压力下流量和占空比关系[18]：

1) 0.2MPa喷雾压力下的喷雾量控制模型为

(12)

2) 0.3MPa喷雾压力下的喷雾量控制模型为

(13)

3) 0.4MPa喷雾压力下的喷雾量控制模型为

(14)

通过MatLab软件进行拟合，可以得到喷头处的压力与流量和占空比的关系式为

(15)

将式(15)代入到喷雾压力系统模型中，得到一个非线性系统，对其进行线性化，得到

q=m1D+m2Pr+m3

(16)

根据系统结构图，假设过滤器阻力为0，根据电磁阀[19]的特性，可以计算出泵后压力值。电磁阀的压力与PWM信号占空比τ(τ=脉冲宽度/脉冲周期)成正比，占空比越大，其相应的控制压力越大。因此，喷头处的喷雾压力即为泵后喷雾压力与占空比的乘积。代入到喷雾压力系统模型中为

(17)

3 最优控制器的设计

为了保证在误差最小、消耗的能量最少的情况下达到最佳的喷雾效果，实现最佳的喷雾压力跟踪过程中的最优跟踪控制，针对喷雾机的特点提出了一种基于能量优化的压力跟踪控制方法，实现了喷雾机压力跟踪误差和能量消耗最小的最优压力跟踪控制。下面结合约翰迪尔4130系列喷雾机的模型对本方法进行具体的介绍。

喷雾机要保证喷雾的均匀性必须要尽可能使跟踪误差达到最小，同时还要保证能量消耗尽可能少。基于上述两点要求，建立系统二次型性能指标如下，即

(18)

基于建立的二次型性能指标，求解最优控制器u(t)，使得喷雾机在完成压力跟踪的前提下，完成压力跟踪误差和能量优化的统一控制。根据系统的喷药压力系统模型整理可得

(19)

占空比D为60%时，喷雾的均匀性为最佳，因此可以转化为

(20)

(21)

其中，w=wc1+wc2。令Bwc2+ρ=0，即wc2=-B-1ρ，则式(21)可以转化为如下状态方程形式

(22)

其中，x=pr，u=wc1。

此时，原非线性系统已经转化为线性系统，所求的非线性系统压力跟踪控制问题转化为线性系统状态调节问题，使系统的求解大大简化。建立二次型性能指标，即

(23)

其中，u任意取值，Q为半正定常数矩阵，R为正定常数矩阵。则有

u*(t)=-R-1BTPx(t)

(24)

最优控制存在且唯一。P为n×n维正定常数矩阵，满足下列黎卡提方程，即

-PA-ATP+PBR-1BTP-Q=0

(25)

其最优方程解为

(26)

x(t0)=x0

(27)

性能泛函的最小值为

(28)

4 仿真实例

为了验证本算法所求得的控制器的调节效果，本文采用MatLab软件对上面设计的喷雾机最优压力跟踪控制策略进行仿真，对不同初始压力进行了仿真验证。

考虑上述所描述的线性系统，对于不同的溶液，体积弹性模量值也有所不同，因此本文以水为例，取kf=2 180MPa；管道内液体的体积=管道截面积乘以管道的长度，本文取为11.4L；kp为泵的容积排量，排量为泵每转1周所排出的液体体积，这里近似等于2个齿轮的齿间容积之和。因此,对于固定型号的离心泵，其容积排量也是固定的，取为168×10-3L/r；经拟合后的m1、m2、m3所对应的系数分别为0.742 3、0.003 923和-0.013 72；占空比D取定值60%。经计算：A=0.45，B=32.13，仿真时间设定为6s。仿真结果如图2～图5所示。

图2 初始压力为0时的跟踪曲线

图3 输出误差e(t)的仿真曲线(e(t)=2)

图4 初始压力为3时的跟踪曲线

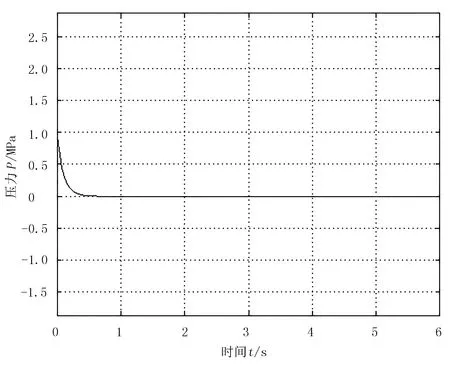
图5 输出误差e(t)的仿真曲线(e(t)=1)

由仿真结果可以看出：即使初始压力值有所不同，控制器也可以在0.5s内快速对转速进行调节，从而实现压力的跟踪控制，进一步证明了本算法的可靠性。

5 结论

本文对植保机喷雾均匀性的影响因素进行了分析，确定了影响喷雾均匀性的主要因素，并就植保机喷雾压力系统模型及最优控制算法展开了具体分析。通过对喷雾压力系统模型进行分析，把系统模型的不确定参数进行分离，并利用相关知识把非线性系统转化为线性系统，利用线性二次型最优控制算法设计最优控制器，并通过仿真算例验证了算控制器的控制效果。