考虑地球曲率情况下测向定位系统中的最优交会角

白 晶，马燕飞，刘晓丽

(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081； 2.中国人民解放军93558部队,河北 石家庄 050081)

0 引言

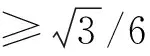
本文在文献[2-3,10]的基础上，在考虑地球曲率的情况下，研究了不同量测误差条件和最小圆概率误差(CEP)准则下被动测向交叉定位系统中的最优交会角。

1 问题描述

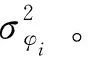
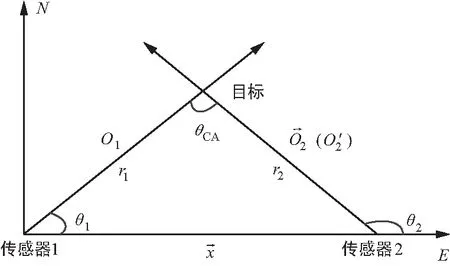
图1 NE平面内的测向交叉定位示意图

根据前面的假设和文献[13-14],得到

(1)

且

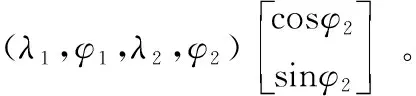
(2)

其中

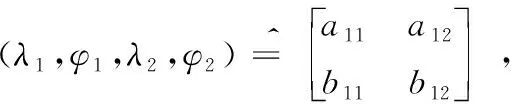
(3)

为坐标变换矩阵且

(4)

其中

为地心固定坐标系到传感器1的局部NED坐标系的坐标转换矩阵。传感器i的地心固定坐标为：

(5)

其中

式中，Re为地球的长半轴，∈为地球偏心率。

从图1可得交叉定位方程

(6)

通过简单计算可得:

(7a)

和

(7b)

根据如图1，目标估计位置为:

(8a)

(8b)

利用式(8)可得:

(9)

其中

η2=cosφ1μ2/μ2,

η4=sinφ1μ2/μ2,

μ1=xNb11cosφ2+xNb12sinφ2-
xEa11cosφ2-xEa12sinφ2,

μ2=xNa12b11sinφ1+xEa11b12cosφ1-
xNa11b12sinφ1-xEa12b11cosφ1,

μ=b11cosφ1cosφ2+b12cosφ1sinφ2-
a11sinφ1cosφ2-a12sinφ1sinφ2。

那么，目标位置估计误差方差为：

(10a)

(10b)

2 最小圆概率意义下的最优交会角

一种常用的度量定位误差的指标是圆概率误差(CEP)。它是指目标落入内部的概率为50%的圆的半径。可表示为[1]：

(11)

其中

(12)

显然，最小化r0.5等价于最小化二元函数f(φ1,φ2)。式(12)两边分别对φ1和φ2求偏导并令它们等于零，可得:

(13a)

(13b)

其中

μ3=b11sinφ1cosφ2+b12sinφ1sinφ2+
a11cosφ1cosφ2+a12cosφ1sinφ2;

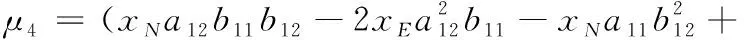
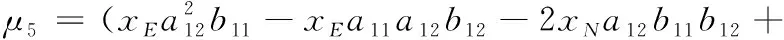
μ6=b11cosφ1sinφ2-b12cosφ1cosφ2-
a11sinφ1sinφ2+a12sinφ1cosφ2。

(14)

(15)

式中，jij(i,j=1,2)为函数fi(φ1,φ2)(i=1,2)对应的雅可比矩阵的元素。根据Fi(i=1,2)的符号可判断稳定点的极值性。

3 数值计算和仿真结果

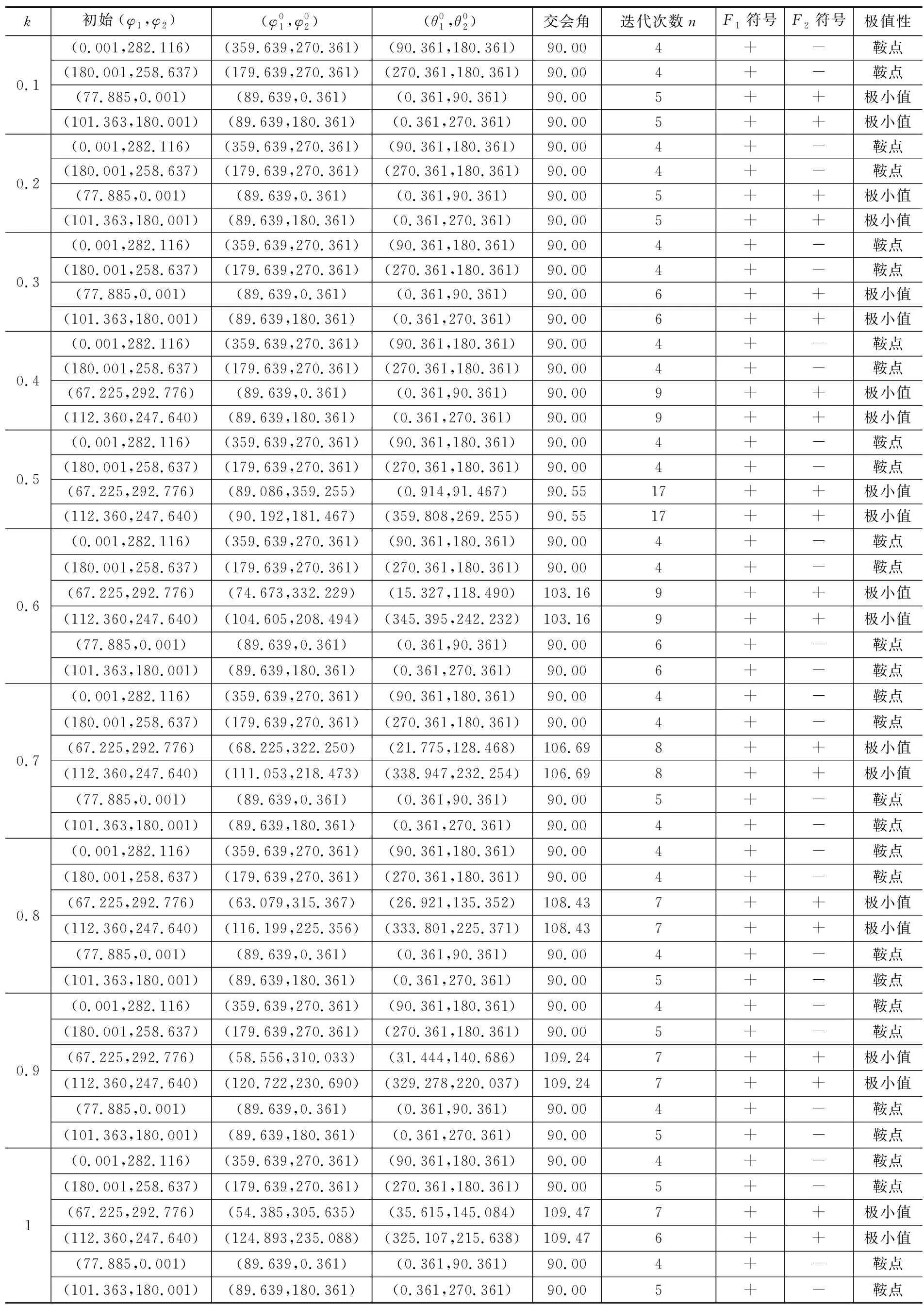
表1 不同k值对应的数值计算结果

图2 最优交会角与方差比值k的关系

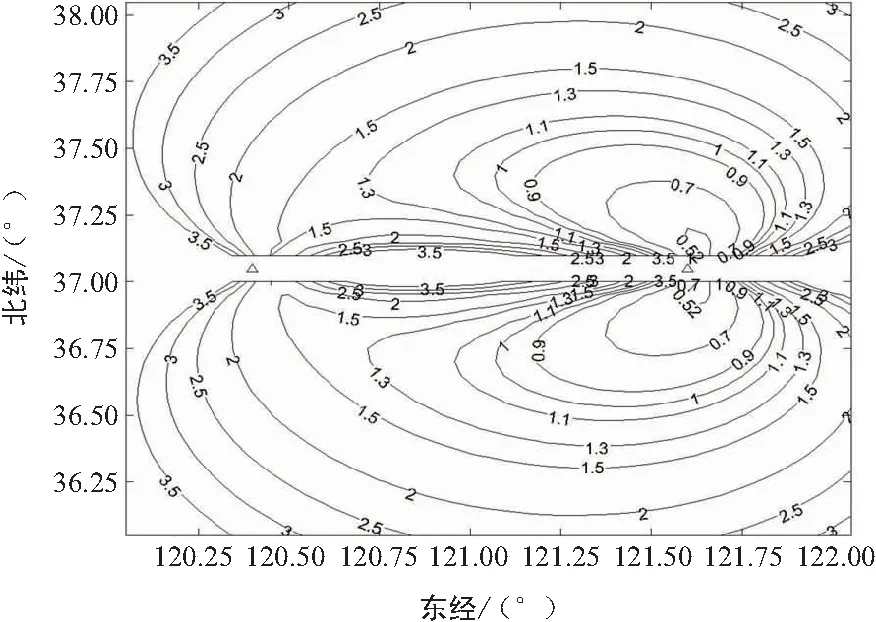
图3 圆概率误差等值线，

图4 圆概率误差等值线，

从图2～图4和表1，可以得出：

① 当k<0.5时，最优交会角近似等于90°。显然，此时CEP值达到最小值的目标位置，无限接近或位于2部传感器的基线上，且无法对目标进行有效测向交叉定位。如图3所示，此时的目标位置无限接近传感器2的位置。因此，此时可行的最优交会角不存在。

② 当k≥0.5时，存在可行的最优交会角，且其值随着方差比值k的增大而增大。对于给定的k，对应2个相同的最优交会角且CEP值达到最小值的2个目标位置对称于E轴。

4 结束语

通过理论分析和数值计算得到，考虑地球曲率时的测线交叉定位系统中的最优交会角与2部被动传感器的角度量测误差方差的比值有关。在实际工程应用中可根据被动传感器的测角误差方差之比，结合量测目标分布情况选择合理的布站方式，以得到高定位精度。文中得到的最优交会角是通过数值计算得到的，所以这里的“最优”不是严格意义下的最优，只是渐进或逼近意义下的最优。同时，为了得到具体的交会角值，前面只给出了几个典型k值对应的最优、次优交会角，这里试图给出一种解决问题的通用方法，可以扩展到任意k值对应的最优、次优交会角的求取。