基于等效燃油消耗理论的增程式电动汽车能量管理策略
2019-12-24王荣华崔俊博酒永胜贺子龙
李 楠, 王荣华, 崔俊博, 酒永胜, 贺子龙
(浙江吉利新能源商用车有限公司, 杭州 311228)
当前增程式电动汽车广泛采用恒温器控制策略,即在行驶过程中分为CD(电量消耗)和CS(电量维持)两种模式[1]。其中在电量维持阶段,因发动机和车轮之间没有机械耦合,一般让增程器始终工作在最优曲线上以获得较好的燃油经济性[2-3]。但是由于整车在不同工况下需求功率随时变化,电池SOC往往会出现急剧升降,将大幅降低电池寿命。实际应用中为避免该情况发生,需要依赖经验及大量的标定试验来优化增程器的工作点和开启时间,而且由于精度的限制,往往还不能使整车性能达到最优[4]。
本文基于实时优化的方法,提出一种等效燃油消耗最小的能量分配策略。在保证车辆动力性和SOC稳定的前提下,以车辆经济性为优化目标,通过计算每一瞬时满足整车动力需求的动力电池和增程器能量分配组合[5-6],筛选出该瞬时工况下燃油消耗最小的点,从而得出不同动力源的最佳分配关系,并结合整车仿真验证该方法的合理性。
1 等效燃油消耗模型
1.1 目标函数
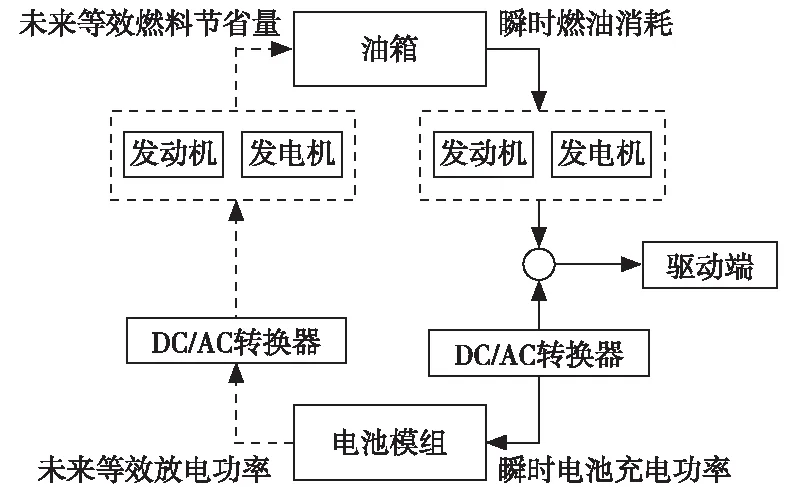
如图1所示,增程式架构从能量看有2条路线,其中一条为增程器路线:发动机带动发电机发电直接供电给驱动电机驱动或者给动力电池充电;另外一条为动力电池路线,动力电池直接供电给驱动电机,同时驱动电机在制动回收时获得电能给动力电池充电[7]。
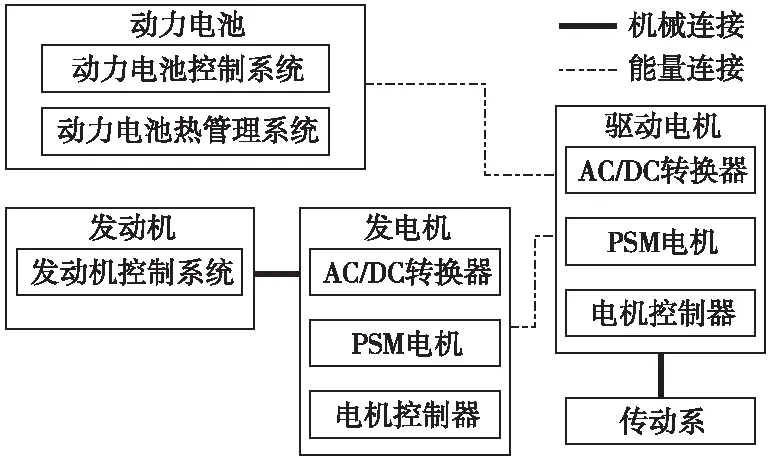
图1 增程式架构示意图
在车辆行驶时,驱动电机输出功率Pv需满足动力需求:
Pv=(Pe+Pb)/ηm
(1)
式中:Pe为增程器输出电功率;Pb为电池充/放电功率;ηm为电机系统效率。
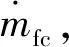
(2)
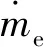
同时式(2)还应满足以下限制(约束)条件:
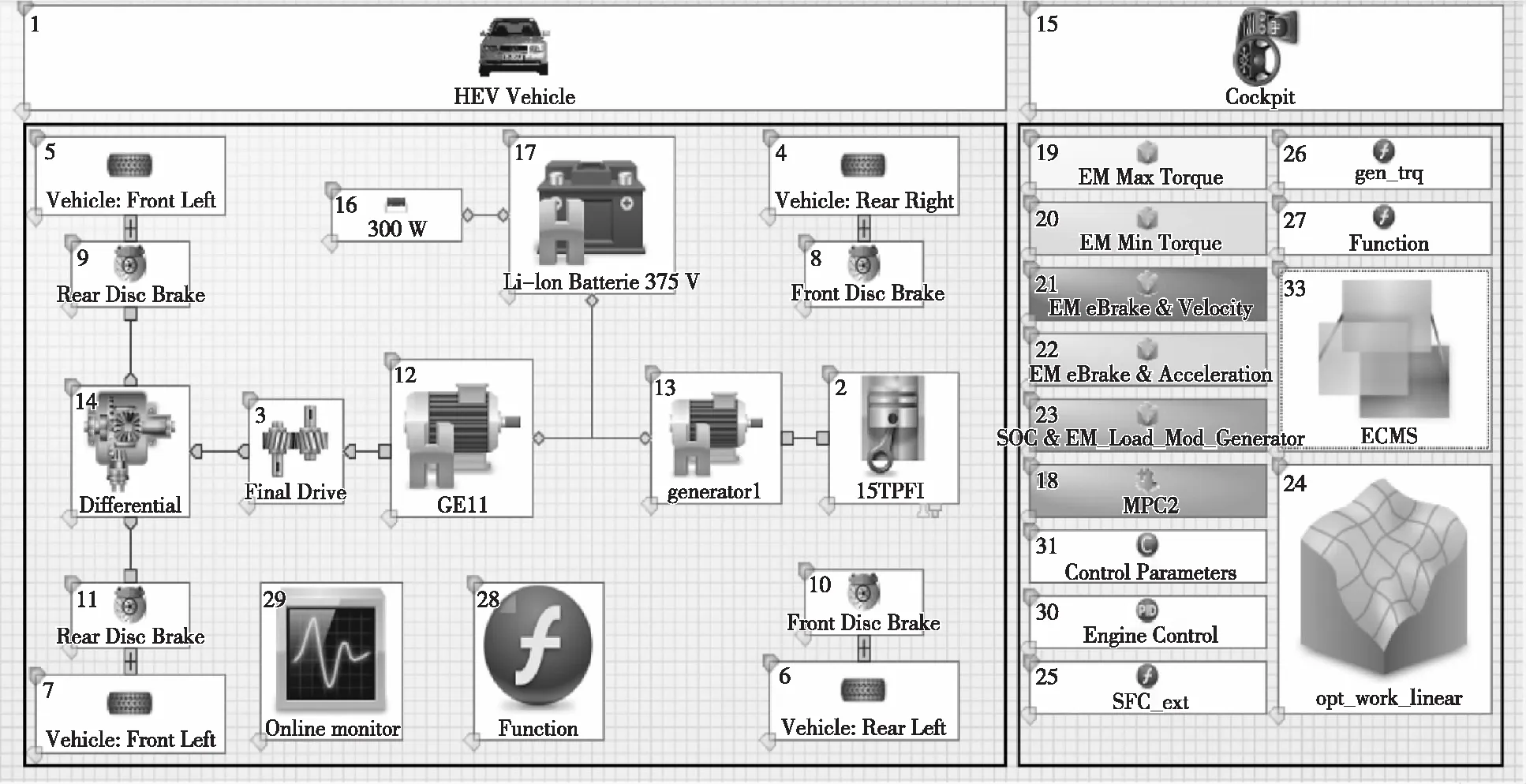
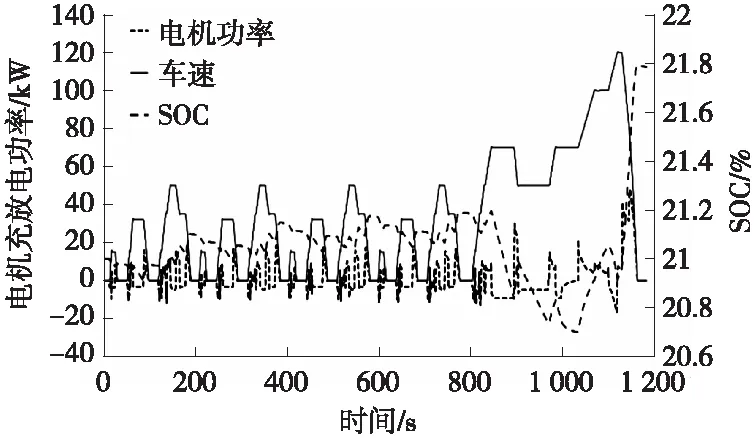
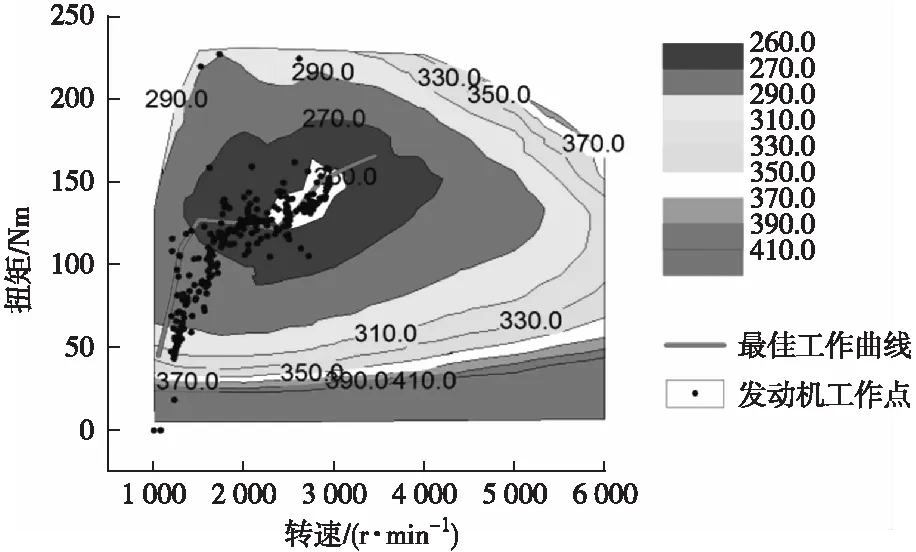
0 (3) 0 (4) Pb_min (5) 式中:SOCh、SOCl为设定的SOC上、下限;SOCacl为当前电池SOC;Pe_max为增程器最大发电功率;Pb_min、Pb_max为动力电池的充放电功率的下限和上限。 如上文所述,按电池充电和放电两种情况来考虑增程式电动汽车的等效燃油模型。 1) 动力电池放电,电能的损失将在未来的某一时刻通过增程器发电来补充,如图2所示。 图2 电池放电等效消耗模型 在该时间段Δt内,电池对外放电功率为Pe_ad,此时电池放出的总能量Eb_ad为: Eb_ad=ΔtPb_ad=ΔtPe_ad/(ηb_dsηad) (6) 式中:Pb_ad为电池模组放电功率;ηb_ds为电池模组放电效率;ηad为放电时DC/AC转换器的效率。 在未来充入电池的能量Eb_fc由未来某一时刻增程器发电的能量和制动回收能量两部分组成: (7) 式中:Pb_fc为未来电池模组的充电功率。 未来时刻油箱需提供的等效消耗的燃料能量Es_fc为: (8) 式中:Pe_fc为未来增程器给电池充电发出的功率;ηe_fc为增程器充电时的系统效率;ηac为充电时DC/AC转换器的效率;ηb_ch为电池模组的充电效率。 则未来消耗的燃油质量mf_fc为: mf_fc=Es_fc/Qfc (9) 式中:Qfc为所用燃料的热值。 则当前电池放电的电能可以等效为未来某一时刻油箱消耗的燃油质量,即: mb_ds=mf_fcEb_ad/Eb_fc (10) (11) 式中:krec为回收能量和发电能量的比值。 2) 动力电池充电,补充的电能将在未来某一时刻通过纯电动行驶以节省燃油消耗,如图3所示。 图3 电池充电等效消耗模型 在该时间段Δt内,增程器以功率Pe_ac给电池充电,电池模组充入的总能量Eb_ac为: Eb_ac=ΔtPb_ac=ΔtPe_acηb_chηac (12) 式中:Pb_ac为当前电池模组的充电功率;ηb_ch为电池模组充电效率;ηac为充电时DC/AC转换器效率。 未来电池模组需要给增程器“补充”的能量Eb_fd为: (13) 式中:Pb_fd为未来电池模组的放电功率。 未来时刻油箱将节约的等效能量Es_fs为: (14) 式中:ηe_fc为增程器充电时的系统效率;ηad为放电时DC/AC转换器效率;ηb_ds为电池模组的放电效率。 未来节约的燃油质量mf_fs可以表示为: mf_fs=Es_fs/Qfc (15) 则当前电池充电补充的电能可以等效为未来节省的等效燃油质量mb_ch: mb_ch=mf_fsEb_ac/Eb_fd (16) (17) 为了保证SOC在一定范围内变化,在上式的基础上添加一个SOC的修正函数,该函数可以在SOC较低的情况下增加等效燃油的权值,减少电能消耗;而在SOC较高的情况下减小等效燃油的权值,增加电能消耗,具体如下[10]: KΔsoc=1-aΔSOC3+bΔSOC4 (18) (19) 式中:a,b为权值系数;SOCact为当前值;SOCh、SOCl分别为设定的SOC上、下限。 综合上述,整车在任一时刻行驶的等效燃油消耗量可以改写为: (20) 以某型增程式城市物流车为研究对象,整车总质量2 900 kg,电池容量51 Ah,驱动电机峰值功率130 kW,增程器最大输出功率65 kW,空气阻力0.37,迎风面积3 m2,滚阻系数0.012。将电池充放电功率作为控制变量,以1 kW为计算步长;仿真中电池的平均放电效率ηb_ds为0.97,平均充电效率ηb_ch为0.95;DC/AC转换器在放电和充电条件下平均效率均为0.975;SOC的上下限值SOCh和SOCl分别设定为25%和17%。根据式(20)分别计算每个步长下增程器和电池的等效燃油消耗量并筛选出最小值,将计算结果整理成插值表以方便后续仿真模型调用。 在AVL CRUISE软件环境下搭建整车仿真模型,如图4所示,并将上述的等效燃料消耗插值表集成到模型中,在NEDC工况下进行实时仿真分析。 仿真结果如图5所示,从图5可以看出:整个工况下SOC基本保持平稳,除了在工况最后一段由于高负荷的能量回收导致电池SOC出现上升趋势,其余时间SOC变化值基本在±0.4%之间浮动,电池SOC总体保持平衡,避免了急剧变化的情况发生。 从图6发动机工作点分布图可以看出:由于整个策略考虑的是等效燃油消耗的总和最小,在该工况下发动机基本工作在最佳工作曲线周围,而非直接落在该曲线上。在仿真环境下对比等效燃油消耗最小策略和原车上搭载的恒温器策略,油耗值由原车的百公里8.41 L降到百公里7.07 L,在经济性上有显著提高。 图4 整车模型 图5 电池工作曲线 图6 发动机工作点分布 本文研究结果表明,等效燃油消耗最小是一种可以工程实现的实时优化策略。该方法在满足整车动力性的前提下,可以将电池SOC稳定在规定的区间内,且经济性优于传统的恒温器式能量分配方法。本文在模型中没有考虑增程器的扭矩响应问题,未来将继续完善该模型研究。同时在研究中也发现,等效燃油消耗策略在不同行驶工况的表现不一致,应分别优化该策略。1.2 等效燃油消耗模型
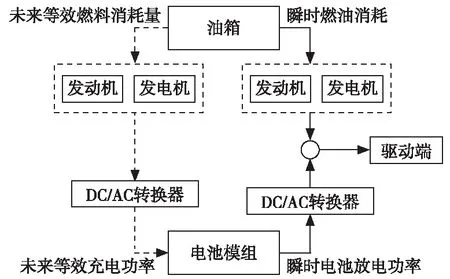
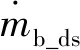
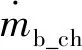
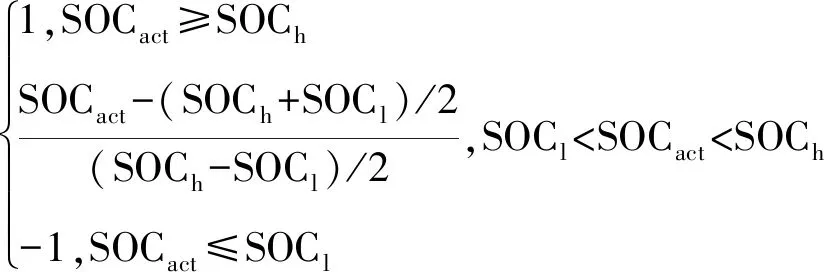
2 等效燃油消耗模型仿真
3 结束语
