基于Levy飞行的萤火虫模糊聚类算法

刘晓明 沈明玉 侯整风

摘 要：针对模糊C均值（FCM）聚类算法易受初始聚类中心影响而陷入局部最优问题，提出了一种基于Levy飞行的萤火虫模糊聚类算法（LFAFCM）。该算法改变萤火虫算法的随机移动策略，以平衡算法局部搜索和全局搜索能力;萤火虫位置更新过程中引入Levy飞行机制，以提高全局寻优能力;根据迭代次数和萤火虫位置动态调整每个萤火虫的尺度系数，以限制Levy飞行可搜索范围，并加快算法收敛速度。利用5个UCI数据集对算法进行实验验证，实验结果表明，该算法有效避免了陷入局部最优并具有较快的收敛速度。

关键词：Levy飞行;尺度系数;萤火虫算法;模糊C均值聚类算法;动态调整

中图分类号：TP301.6

文献标志码：A

Firefly fuzzy clustering algorithm based on Levy flight

LIU Xiaoming*， SHEN Mingyu， HOU Zhengfeng

School of Computer and Information， Hefei University of Technology， Hefei Anhui 230009， China

Abstract：

Fuzzy CMeans （FCM） clustering algorithm is sensitive to the initial clustering center and is easy to fall into local optimum. Therefore， a Firefly Fuzzy CMeans clustering Algorithm based on Levy flight （LFAFCM） was proposed. In LFAFCM， the random movement strategy of firefly algorithm was changed to balance the algorithms local search and global search capabilities， the Levy flight mechanism was introduced during the firefly position update process to improve the global optimization ability， and the scale coefficient of each firefly was dynamically adjusted according to the number of iterations and the firefly position to limit the searchable range of Levy flight and speed up the convergence of the algorithm. The algorithm was validated by using five UCI datasets. The experimental results show that the algorithm avoids the local optimum and has a fast convergence speed.

Key words：

Levy flight; scale factor; Firefly Algorithm （FA）; Fuzzy CMeans （FCM） clustering algorithm; dynamic adjustment

0 引言

聚類是将数据集分成多个不同的类别，使得类中数据尽量相似，类间数据差别较大。聚类作为一种数据分析技术，广泛应用于数据挖掘、机器学习等领域[1]。聚类分为硬聚类和模糊聚类，硬聚类中某个对象只能严格属于某一类，各类之间界限分明。而现实世界中大多数事物并不是非此即彼的关系，事物之间存在不确定性。模糊聚类通过隶属度描述事物属于某个类的程度，更适合描述现实世界事物间的不确定性[2]。模糊C均值（Fuzzy CMeans， FCM）[3]聚类是一种经典的模糊聚类算法，该算法简单，且局部搜索能力强，但对初始值敏感，易陷入局部最优。针对这一问题，一些学者采用群智算法对FCM进行优化，文献[4]中提出基于遗传算法（Genetic Algorithm， GA）的GAFCM（Fuzzy CMeans clustering algorithm based on GA），利用遗产变异操作对聚类中心进行优化;文献[5]提出基于粒子群优化（Particle Swarm Optimization， PSO）算法的PSOFCM（Fuzzy CMeans clustering algorithm based on PSO），利用粒子群优化算法的记忆搜索提高全局寻优能力;但由于粒子群算法和遗传算法收敛速度慢，PSOFCM和GAFCM在单极值数据集上效果均较差，无法得到精确的全局最优解。文献[6]里利用模糊聚类算法生成PSOFCM的初始解，降低初始解的随机性，优化了粒子群演化的方向;文献[7]将Agnes层次聚类与GAFCM结合，利用层次聚类优化初始聚类中心的选取，克服FCM初始值敏感的缺陷;但这些方法均存在参数设置复杂、收敛速度较慢的缺点。

2008年Yang等[8]提出了萤火虫群智优化算法（Firefly Algorithm， FA），FA模仿自然界萤火虫通过发光来吸引同伴的特性，将搜索和优化的过程模拟成萤火虫吸引和移动的过程。FA比GA和PSO具有更好的寻优能力，且思路简单明了、参数较少，广泛应用于路径规划、图像处理、目标跟踪等众多领域[9-11]。文献[12]中提出基于萤火虫算法的FAFCM（Fuzzy CMeans clustering algorithm based on FA），利用FA对模糊聚类的目标函数进行优化，提高模糊聚类的全局收敛性; 然而，同其他启发式算法一样，FA后期也存在收敛速度较慢和易陷入局部最优等不足。文献[13]将混沌理论与萤火虫算法结合，利用混沌运动的随机性、遍历性、规律性增强随机搜索性能。文献[14]将萤火虫种群分为不同参数的多个子群，各子群萤火虫构建相互学习机制，实现子群间信息交流。文献[15]将遗传算法中的变异操作引入萤火虫算法中，提高种群的多样性。上述方法通过改善搜索方式在一定程度上增强了萤火虫算法的全局收敛性，但增加了算法的复杂程度。

Levy飞行模式是自然界中的生物在未知环境中寻找食物的常用方式，果蝇的觅食路径[16]、人类行为中的Ju/hoansi狩猎模式[17]都表現出Levy飞行的特征。Levy飞行具有频繁短距离搜索和偶尔长距离搜索的特性[8]，能够避免局部最优。然而，Levy飞行的短距离搜索在算法初期收敛速度较慢，后期由于多数解都集中在最优解附近，大范围搜索易偏离最优解，对全局收敛不起作用。

本文提出基于Levy飞行的萤火虫模糊聚类算法（Firefly Fuzzy CMeans clustering Algorithm based on Levy flight， LFAFCM），通过改变萤火虫随机移动策略，在位置更新过程中引入Levy飞行机制，平衡算法的局部和全局搜索能力。频繁短距离搜索可提高局部搜索性能;偶尔长距离搜索能够扩大萤火虫搜索范围，增强全局搜索能力。此外，本文算法根据萤火虫位置和迭代次数动态改变每个萤火虫的尺度系数，控制算法不同时期Levy飞行的搜索范围，提高算法初期发现近似全局最优解的效率，同时避免后期长距离搜索导致偏离最优解问题，提高算法的收敛速度。

1 相关算法

1.1 模糊C均值聚类算法

对于数据集X={x1，x2，…，xn}，其中包含n个对象，每个对象含d个属性，聚类就是将这n个对象划分到c个簇中（2≤c≤n），簇的聚类中心为V={v1，v2，…，vc}，FCM的目标函数定义[2]为：

Jm=∑ni=1umij‖xi-vj‖2 （1）

其中，m为模糊加权指数，控制模糊矩阵的分类程度，一般取m=2，U=[uij]c×n是隶属度矩阵，uij∈[0，1]，表示第j对象隶属于第i个簇的程度，‖xi-vj‖2表示第j对象与第i个聚类中心的欧氏距离。FCM算法就是通过不断迭代优化目标函数，当目标函数最小时即得到最优的聚类结果。算法的基本步骤如下：

步骤1 设置初始聚类数目c和模糊加权系数m，随机初始化c个聚类中心v（0）i（1≤i≤c），设置阈值ε作为算法的结束条件。

步骤2 计算隶属度矩阵：

uij=1∑ck=1‖xi-vj‖‖xi-vk‖2m-1; 1≤i≤c，1≤j≤n （2）

步骤3 更新聚类中心V：

vj=∑ni=1umijxi/∑ni=1umij; 1≤j≤c （3）

步骤4 当更新后的聚类中心与原聚类中心的距离小于给定的阈值ε，算法停止，输出聚类中心和隶属度矩阵;否则，转步骤2。

模糊C均值聚类算法通过不断迭代计算聚类中心和隶属度矩阵得到最优的聚类结果，这是一种基于梯度下降的搜索方法，收敛速度快，局部搜索能力强。但FCM非常依赖初始聚类中心的选取，较差的初始聚类中心易导致算法陷入局部最优。

1.2 萤火虫算法

1.2.1 算法原理

自然界中的萤火虫通过发光吸引异性进行信息交流。文献[8]中根据萤火虫的这种发光特性提出了萤火虫优化算法，该算法的基本思想是每个萤火虫代表一个目标函数的解，萤火虫的亮度表示目标函数解的好坏程度，亮度小的萤火虫向亮度大的萤火虫移动，然后更新自己的亮度，萤火虫个体不断移动的过程即为目标函数的优化过程，通过位置和亮度的不断迭代，最终得到目标函数的最优值。

算法的迭代过程遵循下面3个基本规则：

1）所有的萤火虫不以性别区分，任何一只萤火虫都会被其他的萤火虫吸引。

2）萤火虫会被比自己亮的个体吸引，最亮的个体随机改变自己的位置。两只萤火虫之间距离越近，相互之间的吸引度越高。

3）萤火虫的亮度根据所求解问题的目标函数定义。

1.2.2 算法的数学描述

算法中的两个要素是亮度和吸引度，萤火虫位置越优，亮度越大，吸引亮度小的萤火虫向自己移动;萤火虫之间距离越近，吸引度越大，移动距离越长。

算法的相关描述如下：

1）萤火虫亮度：

Ii∝1J（xi）; 1≤i≤n（4）

其中：Ii为第i只萤火虫的亮度，xi为第i只萤火虫的位置，J（xi）为第i只萤火虫对应的目标函数的值。

2）萤火虫之间的相对吸引度：

β=β0×e-γrij（5）

其中：β是萤火虫i和萤火虫j之间的相对吸引度，β0是最大吸引度，即r=0时的吸引度，γ是光强吸收因子（通常设置常数）。rij为萤火虫i和萤火虫j之间的距离，计算方式为：

rij=‖xi-xj‖=∑dk=1（xik-xjk）2（6）

其中d为所求解问题的维数。

3）萤火虫i被比其明亮的萤火虫j吸引而移动，其位置更新公式为：

xk+1i=xi+β（xj-xi）+αεi（7）

其中：xt+1i是萤火虫更新后的位置;xi、xj分别表示萤火虫i和萤火虫j的位置;αεi是扰动项，目的是增强全局搜索能力，α是尺度系数，εi是服从高斯分布的随机数。

2 基于Levy飞行的萤火虫模糊聚类

2.1 Levy飞行机制

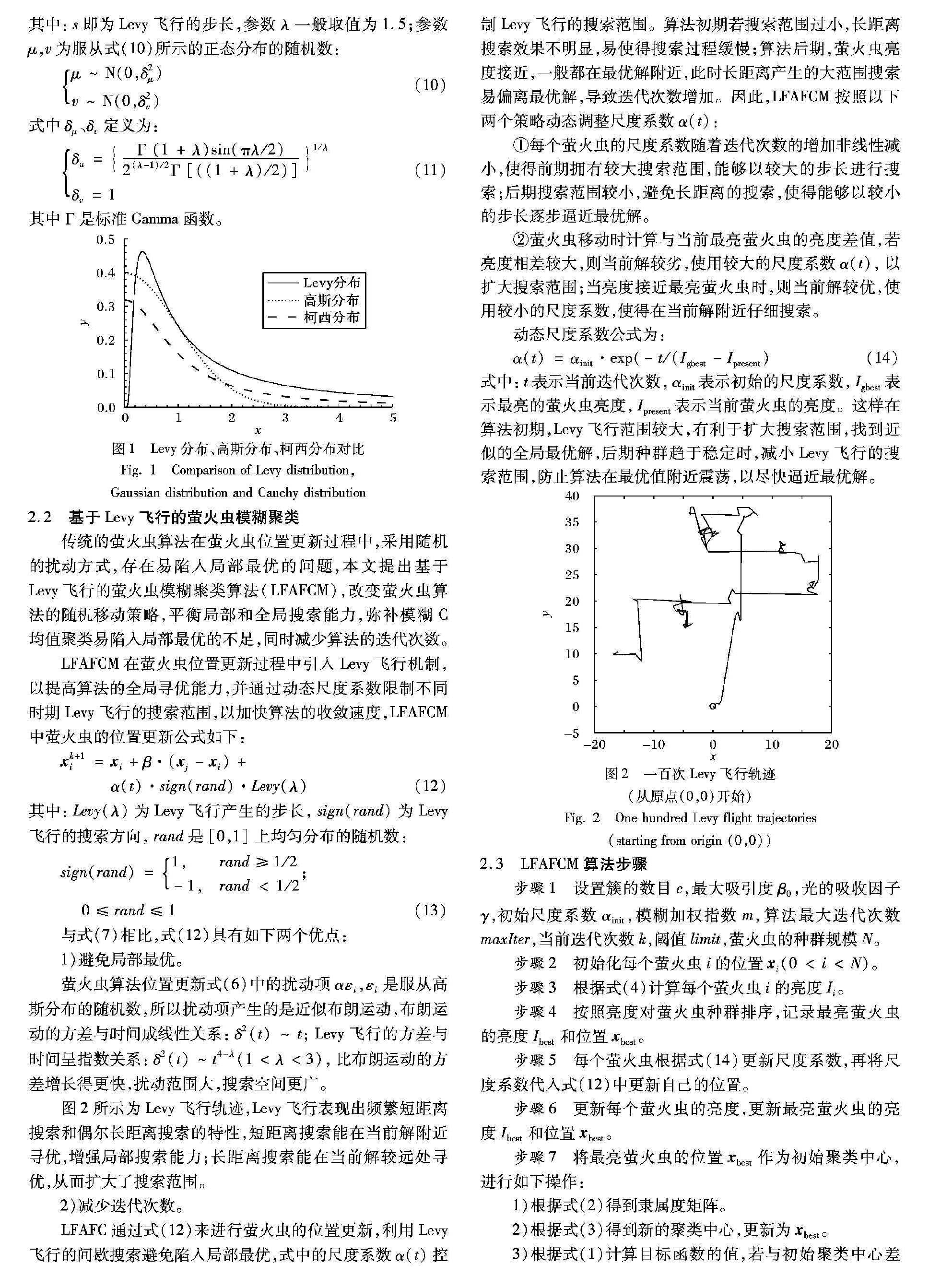
Levy飞行的随机步长服从Levy分布，Levy分布比高斯分布和柯西分布的尾翼更为宽大（如图1所示），具有更强的扰动作用，Levy分布幂次形式的表达式[18]如下：

Levy（λ）～|s|-λ; 1<λ<3 （8）

其中：s是随机步长，λ是指数参数。

Levy飞行的随机步长一般采用Mantegna[19]提出的计算公式：

s=μ/|v|1/λ; 0<λ<2（9）

其中：s即为Levy飞行的步长，参数λ一般取值为1.5;参数μ，v为服从式（10）所示的正態分布的随机数：

μ～N（0，δ2μ）

v～N（0，δ2v）（10）

式中δμ、δv定义为：

δu={Γ（1 + λ）sin（πλ/2）2（λ-1）/2Γ[（（1 + λ）/2）]}1/λ

δv=1（11）

其中Γ是标准Gamma函数。

2.2 基于Levy飞行的萤火虫模糊聚类

传统的萤火虫算法在萤火虫位置更新过程中，采用随机的扰动方式，存在易陷入局部最优的问题，本文提出基于Levy飞行的萤火虫模糊聚类算法（LFAFCM），改变萤火虫算法的随机移动策略，平衡局部和全局搜索能力，弥补模糊C均值聚类易陷入局部最优的不足，同时减少算法的迭代次数。

LFAFCM在萤火虫位置更新过程中引入Levy飞行机制，以提高算法的全局寻优能力，并通过动态尺度系数限制不同时期Levy飞行的搜索范围，以加快算法的收敛速度，LFAFCM中萤火虫的位置更新公式如下：

xk+1i=xi+β·（xj-xi）+

α（t）·sign（rand）·Levy（λ）（12）

其中：Levy（λ）为Levy飞行产生的步长，sign（rand）为Levy飞行的搜索方向，rand是[0，1]上均匀分布的随机数：

sign（rand）=

1，rand≥1/2

-1，rand < 1/2;

0≤rand≤1 （13）

与式（7）相比，式（12）具有如下两个优点：

1）避免局部最优。

萤火虫算法位置更新式（6）中的扰动项αεi，εi是服从高斯分布的随机数，所以扰动项产生的是近似布朗运动，布朗运动的方差与时间成线性关系：δ2（t）～t;Levy飞行的方差与时间呈指数关系：δ2（t）～t4-λ（1<λ<3）， 比布朗运动的方差增长得更快，扰动范围大，搜索空间更广。

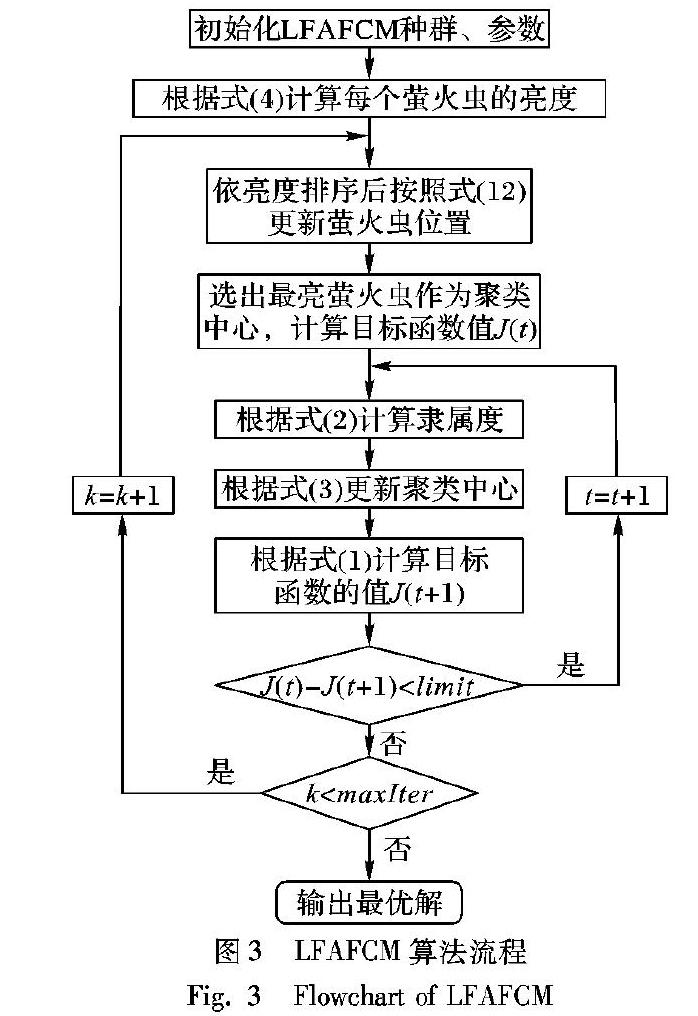
图2所示为Levy飞行轨迹，Levy飞行表现出频繁短距离搜索和偶尔长距离搜索的特性，短距离搜索能在当前解附近寻优，增强局部搜索能力;长距离搜索能在当前解较远处寻优，从而扩大了搜索范围。

2）减少迭代次数。

LFAFC通过式（12）来进行萤火虫的位置更新，利用Levy飞行的间歇搜索避免陷入局部最优，式中的尺度系数α（t）控制Levy飞行的搜索范围。算法初期若搜索范围过小，长距离搜索效果不明显，易使得搜索过程缓慢;算法后期，萤火虫亮度接近，一般都在最优解附近，此时长距离产生的大范围搜索易偏离最优解，导致迭代次数增加。因此，LFAFCM按照以下两个策略动态调整尺度系数α（t）：

①每个萤火虫的尺度系数随着迭代次数的增加非线性减小，使得前期拥有较大搜索范围，能够以较大的步长进行搜索;后期搜索范围较小，避免长距离的搜索，使得能够以较小的步长逐步逼近最优解。

②萤火虫移动时计算与当前最亮萤火虫的亮度差值，若亮度相差较大，则当前解较劣，使用较大的尺度系数α（t），以扩大搜索范围;当亮度接近最亮萤火虫时，则当前解较优，使用较小的尺度系数，使得在当前解附近仔细搜索。

动态尺度系数公式为：

α（t）=αinit·exp（-t/（Igbest-Ipresent）（14）

式中：t表示当前迭代次数，αinit表示初始的尺度系数，Igbest表示最亮的萤火虫亮度，Ipresent表示当前萤火虫的亮度。这样在算法初期，Levy飞行范围较大，有利于扩大搜索范围，找到近似的全局最优解，后期种群趋于稳定时，减小Levy飞行的搜索范围，防止算法在最优值附近震荡，以尽快逼近最优解。

2.3 LFAFCM算法步骤

步骤1 设置簇的数目c，最大吸引度β0，光的吸收因子γ，初始尺度系数αinit，模糊加权指数m，算法最大迭代次数maxIter，当前迭代次数k，阈值limit，萤火虫的种群规模N。

步骤2 初始化每个萤火虫i的位置xi（0

步骤3 根据式（4）计算每个萤火虫i的亮度Ii。

步骤4 按照亮度对萤火虫种群排序，记录最亮萤火虫的亮度Ibest和位置xbest。

步骤5 每个萤火虫根据式（14）更新尺度系数，再将尺度系数代入式（12）中更新自己的位置。

步骤6 更新每个萤火虫的亮度，更新最亮萤火虫的亮度Ibest和位置xbest。

步骤7 将最亮萤火虫的位置xbest作为初始聚类中心，进行如下操作：

1）根据式（2）得到隶属度矩阵。

2）根据式（3）得到新的聚类中心，更新为xbest。

3）根据式（1）计算目标函数的值，若与初始聚类中心差值大于给定阈值limit，转操作1）。

步骤8 若k

LFAFCM算法流程如图3所示，其中J表示目标函数值，t表示梯度下降法中的迭代计数。

2.4 时空复杂度分析

2.4.1 时间复杂度分析

由图3可知，LFAFCM算法的主要部分在步骤5～7，此部分包括两个循环，外循环最大迭代次数为maxIter;内循环设置阈值limit，无准确迭代次数，设内层的平均迭代次数为avgIter;步骤5中每个萤火虫都要向更亮的个体进行移动，由于萤火虫种群规模为N，要进行（N2-N）/2次移动。所以经过所有步骤后，算法的时间复杂度近似为O（maxIter×avgIter×N2）。

2.4.2 空间复杂度分析

设LFAFCM算法萤火虫规模为N，簇的数目为c，迭代次数为maxIter。算法运行过程中，X[C][N]存储萤火虫的自身位置，L[N]存储每个萤火虫的亮度，隶属度矩阵大小U[C][N]，每次迭代后的最亮萤火虫位置保存在B[maxIter]中。因此，LFAFCM算法空间复杂度为2×O（CN）+O（N）+O（maxIter）。

3 实验

实验环境 操作系统Windows 10，语言Python 3.5.5，软件Visual Studio Code 1.28，Matlab R2016b，CUP Inter Core i5，内存 8GB。

实验目的 验证LFAFCM算法的聚类效果和效率。

数据集 本文选取了UCI数据库中的Iris、Wine、Ecoli、Glass、D31五个数据集进行实验，5个数据集的样本数、属性数、类别数如表1所示。

实验结果与分析：

1）数据集的极值。

為了分析LFAFCM算法得到的解是否是全局最优解，先进行实验测试每个数据集的极值，通过在每个数据集上执行1-000次FCM，得到各数据集的极值如表2所示。根据数据集的极值数量，将数据集分成单极值数据集和多极值数据集。

2）LFAFCM聚类效果。

LFAFCM参数设置为γ=1.0，αinit=1.0，β=1.0，模糊权重系数m=2，最大迭代次数maxIter=100，种群规模N=20;GAFCM的N=20，maxIter=100，交差概率pc=0.9，变异概率pm=0.001;PSOFCM的N=20，maxIter=100，惯性权重ω=1，学习因子c1=c2=2;FAFCM中N=20，maxIter=100，β=1.0，γ=0.9，α=0.1，k=2。

算法在每个数据集上重复运行50次，计算目标函数的平均值和标准差，实验结果如表3所示（其中GAFCM、PSOFCM部分实验数据源于文献[20]）。

从表3可以看出，LFAFCM与PSOFCM、GAFCM相比，在各数据集上目标函数都具有更小的平均值和标准差，表明LFAFCM的聚类准确度和稳定性均优于PSOFCM和GAFCM;LFAFCM与FAFCM相比，在单极值数据集Iris、Wine平均值和标准差无明显差异，

但在多极值数据集Ecoli、Glass、D31上，LFAFCM的平均值小于FAFCM，LFAFCM表现出比FAFCM更好的收敛效果，并且LFAFCM的标准差远小于FAFCM，表明LFAFCM稳定性远高于FAFCM。对比表2中数据集的极值，LFAFCM的目标函数平均值与各数据集的最小极值接近，且LFAFCM的目标函数值的标准差极小，表明LFAFCM无论在单极值数据集还是多极值数据集都能稳定得到较好的聚类效果。

为更直观地对比算法的聚类结果，选取数据集D31上各算法50次实验中目标函数值最小的聚类结果，如图4所示，每个聚簇用不同的颜色表示。可以看出，图（a）～（c）中均存在聚簇重叠和明显的分类不合理的地方，而图（d）中没有明显的聚簇错误，基本上可以认为达到了全局最优解。

4）LFAFCM收敛速度。

GAFCM、PSOFCM、FAFCM、LFAFCM在五个数据集上目标函数随迭代次数的变化曲线，如图5所示。

由图5可知，LFAFCM与FAFCM相比，在单极值数据集Iris、Wine上，具有相似迭代变化曲线;在多极值数据集Ecoli、Glass、D31上，LFAFCM目标函数值随迭代次数下降更快，表明LFAFCM比FAFCM具有更快的收敛速度。而LFAFCM与PSOFCM、GAFCM相比，无论在单极值数据集还是多极值数据集上，LFAFCM都表现出更快的收敛速度。

在各数据集的50次实验中，GAFCM、PSOFCM、FAFCM、LFAFCM达到收敛时的平均迭代次数如表4所示。

在数据集Iris、Wine、Glass上，LFAFCM的迭代次数与FAFCM相差不大，但明显少于PSOFCM、GAFCM。在Ecoli、D31数据集上，LFAFCM的迭代次数均远小于其他三种算法。

4 结语

本文针对模糊C均值聚类算法全局搜索能力较差、易陷入局部最优的问题，提出一种基于Levy飞行的萤火虫模糊聚类算法，在萤火虫算法中引入Levy飞行机制，改变萤火虫算法的扰动方式，利用Levy飞行的长短间歇搜索模式增强算法的全局搜索性能。为避免Levy飞行在算法后期飞行范围较大导致收敛速度缓慢，提出动态的尺度系数策略，根据萤火虫的迭代次数和位置动态改变尺度系数，提高算法的收敛速度。通过UCI数据库中五个数据集上的测试，并将本文算法与GAFCM、PSOFCM、FAFCM进行对比，实验结果表明，本文提出的基于Levy飞行的萤火虫模糊聚类无论是在单极值数据集还是多极值数据集上都表现了较强的寻优能力，有效防止了算法陷入局部最优，且运行效率高。

参考文献 （References）

[1]AGGARWAL C C， REDDY C K . Data Clustering： Algorithms and Applications[M]. [S.l.]： Chapman & Hall/CRC， 2013：30-31.

[2]耿嘉艺，钱雪忠，周世兵. 新模糊聚类有效性指标[J]. 计算机应用研究， 2019， 36（4）： 1001-1005. （GENG J Y， QIAN X Z， ZHOU S B， New fuzzy clustering validity index[J]. Application Research of Computers，2019，36（4）： 1001-1005.）

[3]DUNN J C. A fuzzy relative of the ISODATA process andit is use in detecting compact well separated cluster[J]. Journal of Cybernetics， 1973， 3（3）： 32-57.

[4]HALL L O， OZYURT I B， BEZDEK J C. Clustering with a genetically optimized approach[J]. IEEE Transactions on Evolutionary Computation， 1999， 3（2）：103-112.

[5]DE FALCO I， CIOPPA A D， TARANTINO E. Facing classification problems with particle swarm optimization[J]. Applied Soft Computing， 2007， 7（3）：652-658.

[6]耿宗科，王长宾，张振国. 基于模糊Cmeans与自适应粒子群优化的模糊聚類算法[J]. 计算机科学， 2016， 43（8）：267-272. （GENG Z K， WANG C B， ZHANG Z G. Fuzzy Cmeans and adaptive PSO based fuzzy clustering algorithm[J]. Computer Science， 2016， 43（8）： 267-272.）

[7]唐成华，刘鹏程，汤申生，等. 基于特征选择的模糊聚类异常入侵行为检测[J]. 计算机研究与发展， 2015， 52（3）：718-728. （TANG C H， LIU P C， TANG S S， et al. Anomaly intrusion behavior detection based on fuzzy clustering and features selection[J]. Journal of Computer Research and Development， 2015， 52（3）： 718-728.）

[8]YANG X. Firefly algorithms for multimodal optimization[C]// Proceedings of the 5th International Conference on Stochastic Algorithms， LNCS 5792. Berlin： Springer， 2009：169-178.

[9]王晔娇，周晖. 基于混合萤火虫算法的RFID网络多目标规划[J]. 计算机应用研究， 2018， 35（10）：3003-3006. （WANG Y J， ZHOU H. Hybridized firefly algorithm based RFID network multiobjective planning[J]. Application Research of Computers， 2018， 35（10）： 3003-3006.）

[10]HE L， HUANG S. Modified firefly algorithm based multilevel thresholding for color image segmentation[J]. Neurocomputing， 2017， 240：152-174.

[11]de LIMA VARELA V P， OLIVEIRA A， RODRIGUES P， et al. qFA： an optimized basedtracking approach using firefly algorithm[C]// Proceedings of the IEEE 7th Brazilian Conference on Intelligent Systems. Piscataway： IEEE， 2018：302-306.

[12]林睦纲，刘芳菊，童小娇. 一种基于萤火虫算法的模糊聚类算法[J].计算机工程与应用， 2014， 50（21）：35-38， 73. （LIN M G， LIU F J， TONG X J. Fuzzy clustering algorithm based on firefly algorithm [J]. Computer Engineering and Applications， 2014， 50（21）： 35-38， 73.）

[13]张亚楠，刘升. 一种基于混沌云模型的人工萤火虫优化算法[J]. 小型微型计算机系统， 2015， 36（11）：2609-2613. （ZHANG Y N， LIU S. Glowworm swarm optimization algorithm based on chaos cloud model[J]. Journal of Chinese Computer Systems， 2015， 36（11）： 2609-2613.）

[14]符强，童楠，赵一鸣. 一种基于多种群学习机制的萤火虫优化算法[J].计算机应用研究， 2013， 30（12） ：3600-3602. （FU Q， TONG N， ZHAO Y M. Firefly algorithm based on multigroup learning mechanism[J]. Application Research of Computers， 2013， 30（12） ：3600-3602.）

[15]杜晓昕，张剑飞，孙明. 基于自适应t分布混合变异的人工萤火虫算法[J]. 计算机应用， 2013， 33（7）：1922-1925. （DU X X， ZHANG J F， SUN M. Artificial glowworm swarm optimization algorithm based on adaptive t distribution mixed mutation[J]. Journal of Computer Applications， 2013， 33（7）： 1922-1925.）

[16]REYNOLDS A M， FRYE M A. Freeflight odor tracking in drosophila is consistent with an optimal intermittent scalefree search[J]. PloS One， 2007， 2（4）： No.e354.

[17]BROWN C T， LIEBOVITCH L S， GLENDON R. Lévy flights in Dobe Ju/ foraging patterns[J]. Human Ecology， 2007， 35（1）： 129-138.

[18]VISWANATHAN G M， AFANASYEV V， BULDYREV S V， et al. Lévy flights search patterns of biological organisms[J]. Physica A： Statistical Mechanics and its Applications， 2001， 295（1/2）： 85-88.

[19]MANTEGNA R N. Fast accurate algorithm for numerical simulation of Levy stable stochastic processes[J]. Physical Review E， 1994， 49（5）： 4677-4683.

[20]LI C， ZHOU J， KOU P， et al. A novel chaotic particle swarm optimization based fuzzy clustering algorithm[J]. Neurocomputing， 2012， 83：98-109.

This work is partially supported by the National Natural Science Foundation of China （61572167）.

LIU Xiaoming， born in 1994， M. S. candidate. His research interests include network communication and security.

SHEN Mingyu， born in 1962， Ph. D.， associate professor. His research interests include network and information security.

HOU Zhengfeng，born in 1958， M. S.， professor. His research interests include threshold secret sharing， network security.