GIS专业数据结构课程设计教学内容优化

2019-12-23龙颖波刘远刚何贞铭蔡永香李功权邓帆

计算机时代 2019年12期

龙颖波　刘远刚　何贞铭　蔡永香　李功权　邓帆

摘要： GIS专业的数据结构课程设计实践教学，目标是培养学生解决实际问题的能力，在教学内容上还需兼顾数据结构基础知识与GIS专业问题的衔接与融合，从而体现GIS专业特色。文章针对数据结构课程设计实践教学，在传统教学内容中引入GIS专业的经典问题作为有益补充;设计了新的课程设计选题方案，向学生提供针对不同层次教学目标的三类选题，即基础题、一般应用题和GIS专业应用题;并以栅格数据四叉树压缩编码与解码问题为例，详细说明将数据结构基础知识与GIS专业经典问题结合出题的可行性、设计思路、实现手段及其对教学的促进作用。

关键词：数据结构; 课程设计; 地理信息科学; 四叉树编码

中图分类号：G642 文献标志码：A 文章编号：1006-8228（2019）12-81-04

Optimizing the teaching content of data structure practicum for GIS specialty

Long Yingbo， Liu Yuangang， He Zhenming， Cai Yongxiang， Li Gongquan， Deng fan

（School of Geosciences， Yangtze University， Wuhan， Hubei 430100， China）

Abstract： The practicum of data structure （DS） for students majoring in geographical information science （GIS） aims at cultivating students' ability to solve practical problems， but also should give consideration to the connection and integration of basic knowledge of DS and professional problems of GIS in the teaching content， so as to embody the characteristics of GIS. This paper introduces some classical problems of GIS into the traditional teaching content of course project of DS as a useful supplement. To this end， a new topic-choosing plan is designed to provide students with three types of topics， i.e. basic topics， general application topics and GIS professional application topics， for different levels of teaching objectives. Taking the quadtree compression coding and decoding of raster data as an example， the feasibility， design ideas， implement measures and promoting effects of the integration of basic knowledge of DS and professional problems of GIS in the teaching content are described in detail.

Key words： geographical information science （GIS）; practicum; data structure （DS）; quadtree coding

0 引言

數据结构是一门研究计算机中非数值计算问题的数据组织和编排方式的综合性基础课程[1]。作为地理信息科学（Geographical Information Science， GIS）专业的一门核心基础课程，数据结构的基本理论与方法是GIS软件设计、开发和应用相关专业课程的重要支撑 [2-4]。有必要针对GIS专业的特点和需要对数据结构课程教学内容做进一步优化[5]。无论是面向计算机类专业还是其它信息科学类专业，学习数据结构的首要目的是为了提高应用计算机解决实际问题的能力，培养学生的实践能力是其教学重点[6，7]。在数据结构教学中一般会设置较高比重的实践教学，包括习题作业、上机训练和综合课程设计等。其中，理论课程结束后的课程设计是实践教学的最高层次，其目的是让学生深化理解书本知识，学会把现实世界中的实际问题在计算机内部表示出来，提升实践动手能力和解决实际问题能力。目前，数据结构课程设计可参考的教材一般针对计算机相关专业编写[8-10]，面向GIS专业学生授课时，若全盘照搬这些教材的内容，则不能将这门课的基础知识融入GIS专业课程体系，不利于本课程与GIS专业相关课程的衔接，体现不了GIS专业特色。因此，有必要面向GIS专业的培养目标对数据结构课程设计教学内容进行补充和优化，在数据结构课程设计的教学内容中引入GIS专业的应用问题。这样既培养学生运用数据结构基础知识解决实际问题的能力，也激发学生探索和研究GIS专业问题的兴趣，从而促进学生专业概念和专业思想的形成，为后续专业课的深入学习做准备。

1 选题方案优化

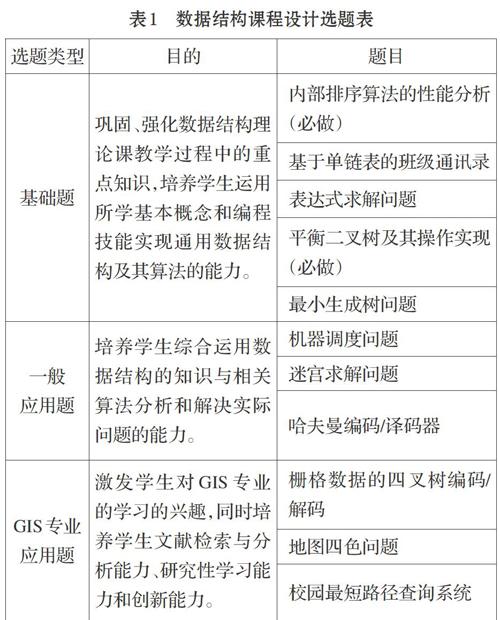
GIS专业数据结构课程设计选题，除了需要覆盖数据结构这门课本身的基础知识点外，还应该结合本专业特点，引入地理空间数据相关的专业问题，形成数据结构基本概念与GIS专业应用方法、技术的无缝结合。因此，将课程设计的选题分为三个层次，包括基础题、一般应用题和GIS专业应用题（见表1）。

基础题的内容均来自数据结构课本，此类题目的实验目的是巩固、强化数据结构理论教学过程中的重点知识，培养学生运用所学基本概念和编程技能实现几种通用数据结构的组织存储方法和常用算法的能力，是对理论课中实践环节的有益补充。

一般应用题比基础题难度略高，要求学生综合运用数据结构的知识与相关算法解决具体应用问题。比如，机器调度、迷宫求解、哈夫曼编码解码等。学生需对问题进行分析抽象，提取核心概念，然后与所学数据结构知识点进行匹配。通过此类题目的演练，培养学生分析和解决实际问题的能力。

GIS专业应用题可涉及GIS相关的地图制图、遥感分析、全球定位导航技术等各领域的经典应用问题，需要学生将数据结构分析设计方法与GIS专业问题融会贯通。例如，矢量数据的多边形自动生成、栅格数据四叉树编码、道路网的最优路径导航、地图制图中的四色渲染等。这些问题对低年级GIS专业学生还有一定难度，需要他们主动查阅专业资料，提前了解相关专业知识，理解其中的核心概念，然后设计出合适的数据存储结构和算法加以解决。通过这个过程，激发学生对GIS专业知识深入学习的兴趣，为后续GIS专业课程的学习铺垫，同时培养学生的文献检索与分析能力、研究性学习能力和创新能力。

2 GIS专业应用题设计

选题方案中的基础题和一般应用题在很多数据结构的实践教材中均有介绍[8-10]，本文不再赘述。GIS专业应用题需要结合GIS专业问题和数据结构相关知识点综合出题。GIS各领域涉及众多空间数据结构，如矢量、栅格数据的组织、空间索引和最短路径算法等[11-12]。但相关教材鲜有将这些空间数据结构与数据结构课程中的基本知识点进行关联，不利于新旧知识之间的迁移与融合。实际上，这些问题经过进一步的分解均可由线性表、树、图等基本数据结构进行抽象表达。出题时需要厘清这些问题与各类基本数据结构之间的对应关系，用通俗易懂的语言描述题目中需要解决的专业问题、解题基本要求和条件，并给出必要的提示信息。

下面以“栅格数据四叉树压缩编码与解码”为例说明GIS专业应用题的设计。栅格数据的四叉树编码是一种经典的压缩编码方式，最早应用于加拿大地理信息系统（CGIS）中，是GIS原理课程中的重要知识点之一，在GIS专业领域有广泛应用[11]。因此，课程组将四叉树编码与解码问题纳入课程设计选题。具体选题设计包括问题描述、基本要求和实现提示三个方面。

⑴ 问题描述

区域型物体的四叉树表示方法，将四叉树结构表达的信息以一种线性编码的方式存储起来，称之为四叉树编码，其在图像分割、数据压缩、地理信息系统等方面应用广泛。请实现二值栅格数据的四叉树压缩编码/解码算法，即设计四叉树数据结构及算法，将给定的二值图像转换为四叉树线性编码方式实现压缩存储，并设计解码算法将压缩编码文件解码还原为二值图像。

⑵ 基本要求

①读取一个待压缩的栅格数据文件（BMP格式），文件中的每个像元仅有（0、1）两种取值（即二值图像），用一个矩阵存储原始数据;

②对该矩阵进行自上而下的四叉树分割，构建四叉树结构;

③对得到的所有叶子节点进行线性四叉树编码，将编码作为一个数组写入文件;

④实现线性四叉树编码的解码程序，即读取压缩编码文件将其还原为栅格图像数据文件。

⑶ 实现提示

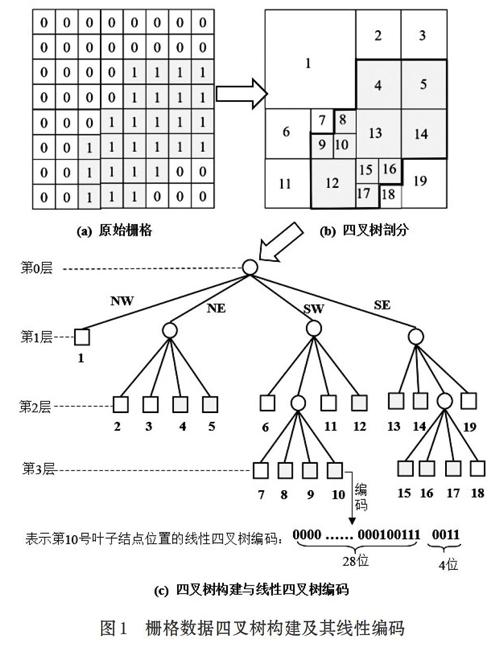
问题的关键在于对栅格数据四叉树剖分、四叉树构建以及线性四叉树编码几个知识点的理解。其中四叉树剖面和线性四叉树编码的基本思路见图1，解码过程与编码正好相反。相关概念与方法描述如下。

①四叉树剖分方法。将图像区域按大小相同的象限四等分，每个象限又可根据一定规则判断是否继续等分为次一层的四个象限。若子象限只含一种属性代码，则停止继续分割。图像区域的栅格阵列应为2n×2n，如果图像不是一个2n×2n的尺寸，通过边缘增补空白行、列的方式凑足。如图1（a）、图1（b），一个8×8的栅格，经过三层四叉树剖分后，得到的每个单元只含有一种属性代码。

②线性四叉树编码方法。如图1（c），四叉树剖分结果逻辑上可用一棵四叉树表示，树中每个非叶子结点有四个分支，每个叶子结点对应的是只含有一种属性代码的剖分区域。线性编码的目的就是记录每个叶结点在四叉树中的位置和值，其中值就是子区的属性代码，所以重点是如何在编码中表达结点的位置。常用的线性四叉树编码方式有：a）基于深度和层次码的方式;b）基于四进制的方式;c）基于十进制的方式。以第一种方式为例，用一个32位的二进制数表示节点的位置，具体分为两部分，最右边4位记录该叶子结点的深度，从右第5位开始往左的28位依次记录从叶节点到根结点的路径。用0、1、2、3分别表示北西（NW）、北东（NE）、南西（SW）和南东（SE）。例如，图1（c）中编号为10的叶子結点在树中位置信息的线性编码为：00000000 00000000 00000010 01110011。

作为GIS专业后继课程中的内容，四叉树及其压缩编码的相关概念对GIS专业二年级的学生可能是全新的，但是却能与数据结构课程所学的知识点之间建立紧密的联系。例如，本题中原始栅格数据的表达，实际上就是数据结构中介绍的二维数组;同时，四叉树编码的结果也可用数组存储;需要构建的四叉树，其实就是二叉树的一种扩展。数据结构课程中，对二叉树作了详细介绍，学生应该可以根据对二叉树的理解去实现四叉树的存储结构和相关操作算法。通过这种训练，可建立数据结构与GIS专业知识之间的深度联系，锻炼学生举一反三的能力。

必须承认，完全依靠低年级学生现有的知识和能力去解决一个对他们来说全新的专业问题，是不太可行的。因此除了要向学生提供必要的提示信息外，还要引导和鼓励他们多查阅专业资料，必要时提供部分辅助程序。例如，针对本选题，我们给学生提供了读写栅格数据文件（BMP格式）的源程序及使用说明，让学生能够从这种基础但不涉及核心问题的代码编写工作中解放出来，集中精力解决主要问题。这样即降低了题目的难度，也可锻炼学生文献研究、探究式学习和模块化程序设计等方面的能力。

3 结语

数据结构教学内容比较抽象，必须理论联系实践，因此课程设计教学是重点。作为GIS专业的一门课程设计，选题不仅需要以基础知识点的巩固和动手能力的提高为主要目的，还要兼顾专业特色。本文将课程设计的选题分三个层次：基础题、一般应用题和GIS专业应用题。在专业应用题中引入GIS专业经典问题，体现了基础性、应用型、专业性和创新性的有机融合，为后序GIS专业课程铺垫。

课程设计的顺利开展需要学生具备一定的编程能力作为支撑。而GIS低年级学生接触编程课程较少，较多学生对程序设计与调试存在畏惧心理，他们很容易由于中途受挫而影响后续学习的信心和兴趣。因此，课程设计也包括理论教学过程中应该多称赞学生，鼓励他们自主调试程序，尽快树立学习自信心。

参考文献（References）：

[1] 严蔚敏，吴伟民.数据结构（C语言版）[M].北京：清华大学出版社，2016.

[2] 吴信才，徐世武，万波，等.地理信息系统原理与方法（第三版）[M]. 北京：电子工业出版社，2014.

[3] 李满春，陈刚，陈振杰，等.GIS设计与实现（第二版）[M].北京：科学出版社，2011.

[4] 郭庆胜，蔡忠亮."GIS工程设计"的实验教学模式研究[J]. 测绘工程，2016。25（9）：77-80

[5] 刘远刚，何贞铭，蔡永香，等.地理信息科学专业数据结构课程教学改革与实践[J].电脑知识与技术，2017.13（17）：96-97

[6] 陈越，何钦铭，冯雁."数据结构"综合性课程设计教学探索与实践[J].计算机教育，2008.8：54-55

[7] 孙歧峰."数据结构"课程教学反思与改革[J].计算机教育，2009.22：66-67，35

[8] 严蔚敏，吴伟民，米宁.数据结构题集（C语言版）[M].北京：清华大学出版社，2008.

[9] 徐雅静，肖波.数据结构与STL习题解析与实验指导[M].北京：北京邮电大学出版社，2015.

[10] 卢玲，陈媛，何波，等.數据结构学习指导及实践教程[M].北京：清华大学出版社，2019