基于区域分割的低覆盖点云配准算法

汤慧 周明全 耿国华

摘 要：针对低覆盖点云配准的时间复杂度高、收敛速度缓慢以及对应点匹配易错等问题，提出一种基于区域分割的点云配准算法。首先，利用体积积分不变量计算点云上点的凹凸性，并提取凹凸特征点集;然后，采用基于混合流形谱聚类的分割算法對特征点集进行区域分割，并采用基于奇异值分解（SVD）的迭代最近点（ICP）算法对区域进行配准，从而实现点云的精确配准。实验结果表明，所提算法通过区域分割可以大幅提高点云区域的覆盖率，并且无需迭代即可计算刚体变换的最佳旋转矩阵，其配准精度比已有算法提高了10%以上，配准时间降低了20%以上。因此，所提算法是一种精度高、速度快的低覆盖点云配准算法。

关键词：点云配准;体积积分不变量;区域分割;奇异值分解;迭代最近点

中图分类号：TP391

文献标志码：A

Low coverage point cloud registration algorithm based on region segmentation

TANG Hui1，2， ZHOU Mingquan1，3*， GENG Guohua1

1.College of Information Science and Technology， Northwest University， Xian Shaanxi 710127， China;

2.Experimental Training Teaching Center， Xian University of Finance and Economics， Xian Shaanxi 710010， China;

3.College of Information Science and Technology， Beijing Normal University， Beijing 100875， China

Abstract：

Aiming at the problems of high time complexity， slow convergence speed and errorprone matching of low coverage point cloud registration， a point cloud registration algorithm based on region segmentation was proposed. Firstly， the volume integral invariant was used to calculate the concavity and convexity of points on the point cloud， and then the concavity and convexity feature point sets were extracted. Secondly， the regions of the feature points were partitioned by the segmentation algorithm based on the mixed manifold spectral clustering， and the regions were registered by the Iterative Closest Point （ICP） algorithm based on Singular Value Decomposition （SVD）， so that the accurate registration of point clouds could be achieved. The experimental results show that the proposed algorithm can greatly improve the coverage of point clouds by region segmentation， and the optimal rotation matrix of rigid body transformation can be calculated without iteration. The algorithm has the registration accuracy increased by more than 10% and the registration time reduced by more than 20%. Therefore， the proposed algorithm can achieve fast and accurate registration of point clouds with low coverage.

Key words：

point cloud registration; volume integral invariant; area segmentation; Singular Value Decomposition （SVD）; Iterative Closest Point （ICP）

0 引言

点云配准是点云数据处理的一个重要研究内容，是后续三维点云重建的技术基础。由于受环境和三维数据采集设备分辨率等多种因素的影响，在对实物数字化时采集到的每个点云数据往往只覆盖了实物模型表面的部分数据信息，而且还存在旋转和平移等刚体变换问题。因此，为了获取物体表面的完整点云数据信息，必须通过点云配准将不同角度的点云数据变换到同一坐标系下。

点云配准的算法有很较多，主要有重心重合法[1]、标定点法[2]以及特征提取法[3-4]等。重心重合法通过将两个点云的重心重合来实现点云配准;标定点法是一种通过在物体表面贴上标定点并利用标定点进行点云配准的方法;特征提取法则是利用物体表面上的一些几何特征，如特征点、曲率、表面纹理以及边缘等，对特征进行提取和描述，通过确定特征之间的对应关系来实现点云配准。

目前应用最广泛的点云配准算法是由Besl 等[5]提出的迭代最近点（Iterative Closest Point， ICP）算法。ICP 算法计算简便直观、配准精度高，但对待配准点云的初始位置的依赖性较强，并要求两个点云之间存在一定的包含关系，因此在实际配准中容易陷入局部最优，导致配准效率不高。为了克服 ICP 算法的局限性，国内外学者对ICP 算法进行了改进研究，相继提出PICP（Probability ICP）算法[6]、IAICP（IntensityAssisted ICP）算法[7]、MICP（Modified ICP）算法[8]以及CICP（Cluster ICP）算法[9]等多种改进的ICP算法。这些配准算法并不具有普适性，特别是对低覆盖率点云的配准效果不佳。

对于低覆盖率的点云，邵红旭[10]提出了一种基于重叠区域的改进ICP配准算法，提高了低覆盖点云的配准精度;Xu等[11]采用结合颜色和深度信息的低覆盖点云配准算法实现了工业机器人的姿态估计; Ding等[12]提出了一种基于自适应距离函数的点云配准算法，通过描述最短点面距离实现低覆盖点云的配准; Wu等[13]提出一种基于X射线斷层扫描的点云配准算法，可以实现不同覆盖率的砂粒碎片的断裂面匹配;Liu等[14]通过分析深度测量误差模型和权重函数实现了低覆盖点云的精确配准。虽然这些低覆盖点云配准算法在一定程度上提高了点云配准的精度，但是仍然存在算法耗时长、鲁棒性低等缺点。

针对低覆盖点云配准的时间复杂度高、收敛速度缓慢、对应点匹配易错等问题，本文提出一种基于区域分割的点云配准算法。首先，采用体积积分不变量计算点的凹凸性，并提取凹凸特征点;然后，对特征点集进行区域分割，并将奇异值分解（Singular Value Decomposition， SVD）应用到ICP算法中，以此实现区域特征点集的配准。该算法无需迭代即可计算两个特征点集的刚体变换，具有较高的配准精度和配准速度。

1 提取凹凸特征点

由于体积积分不变量可以稳定且多尺度地描述点云表面的凹凸程度[10]，因此采用体积积分不变量可以判断其点的凹凸性，并提取凹的和凸的特征点。设Q代表一个单位球，p+rQ表示半径是r、中心是点p的球。那么体积积分不变量Vr（p）定义为

Vr（p）=∫p+rQg（x）w（p-x）dx（1）

式中： g（x）表示特征函数，w（p-x）表示权重函数。

将式（1）中的特征函数g（x）换成ID（x），并令w（p-x）=1，则体积积分不变量Vr（p）的计算式转化为：

Vr（p）=∫p+rQID（x）dx（2）

特征函数ID（x）的含义为：当x在曲面外侧，ID（x）=1;当x在曲面内侧，ID（x）=0。Vr（p）的几何意义就是球p+rQ在曲面外侧的体积，如图1所示。

由图1可知，Vr（p）反映了曲面在p点处的凹凸程度。当Vr（p）=2πr3/3 时，即Vr（p）是球体积的一半时，p在半径r邻域内为平面顶点。当半径r越大，Vr（p）越大，且p+rQ内部噪声与Vr（p）无关。

顶点的凹凸程度采用点的体积积分不变量与球体积的比值来定义，定义式为：

charV（p）=Vr（p）V（Q）=34πr3∫p+rB1D（x）dx（3）

于是有，当charV（p）=0.5时，点p位于平坦面;当charV（p）>0.5，点p位于凸面;charV（p）<0.5，点p位于凹面。

本文提取的特征点即为以上计算的凹凸特征点。

2 特征点区域分割

对于上述提取的凹凸特征点，采用一种基于混合流形谱聚类的分割算法[15]对其进行区域分割。该算法通过对特征点构建邻接矩阵实现特征点向无向图中节点的转换，并将点的对应关系转换成无向图中的连线，从而将特征点的区域分割问题转换为谱空间的聚类问题。

首先利用混合概率主成分分析（Mixtures of Probabilistic Principal Component Analysis， MPPCA）法[16]提取特征点之间的几何关系，并构造邻接矩阵。MPPCA采用M个线性主成分分析（Principal Component Analysis， PCA）来描述点云结构，可以有效避免PCA对特征点集的类椭圆分布的要求，同时增强对复杂几何结构点云的分析能力。MPPCA利用最大期望（Expectation Maximization， EM）算法[17]得到最优描述点云分布的M个线性主成分分析器和每个点xi对应于M个线性主成分分析器的概率密度分布。

对于第m个线性主成分分析器，假设任意一个点xi对应于一个降维后的点yi， 计算式为：

xi=Vmyi+μm+εm（4）

式中： Vm表示第m个主成分分析器的主子空间，μm表示分布于第m个分析器的所有点的均值;εm表示噪声。

假设yi和εm均服从高斯分布，那么xi关于m的条件概率为

p（xi|m）=（2π）-32|U|-12exp[-12ZTU-1Z]（5）

式中：Z=xi-μm，U=σ2mI+VmVmT。

目标函数FMPPCA就是第m个主成分分析器上任意点xi的最大似然估计，计算式为：

FMPPCA=∑Ni=1ln[∑Mm=1πm p（xi|m）]（6）

式中，πm为各个主成分分析器的混合比例，πm≥0，Mm=1πm=1。

描述点云的最佳参数通过利用EM算法使目标函数FMPPCA最大化来求解。将混合比例最大的主成分分析器作为点的所在流形，那么点i与点j之间的相似关系计算式为

2）将SVD用于测量模式矩阵，即Ap=SVDUApΣApVApT，并计算旋转矩阵R（j）=VApUM（j）T;

3）创建旋转模式（j）p=R（j）TAp[p1，p2，…，pN]，并根据B（j）q的最近点qj构建（j）q=[（j）1，（j）2，…，（j）qN];

4）计算配准误差ε（j）=‖（j）q-（j）p‖F。若ε（j）小于给定阈值则说明两个点云区域{Ap，Bq}配准成功，否则区域对{Ap，Bq}为不可配准的区域。

采用上述的特征点区域对配准方法，采用穷举法将区域集合{A1，A2，…，As}和{B1，B2，…，Bt}中区域进行两两配准即可实现初始点云点云M和D的最终配准。

4 实验与结果分析

本文算法在Visual studio 2010环境下，Intel Core i7 3.33GHz的CPU、16GB内存的Windows 7 64位PC上进行了实现，并且应用到了不同覆盖率的公共点云数据模型bunny和dragon的配准，以及文物碎块点云数据模型的断裂面匹配中。实验所用数据均为采用三维激光扫描仪获取的点云数据模型或由三角网格数据模型转化的点云数据模型，模型均满足简单的三维刚体变换。

4.1 公共点云配准

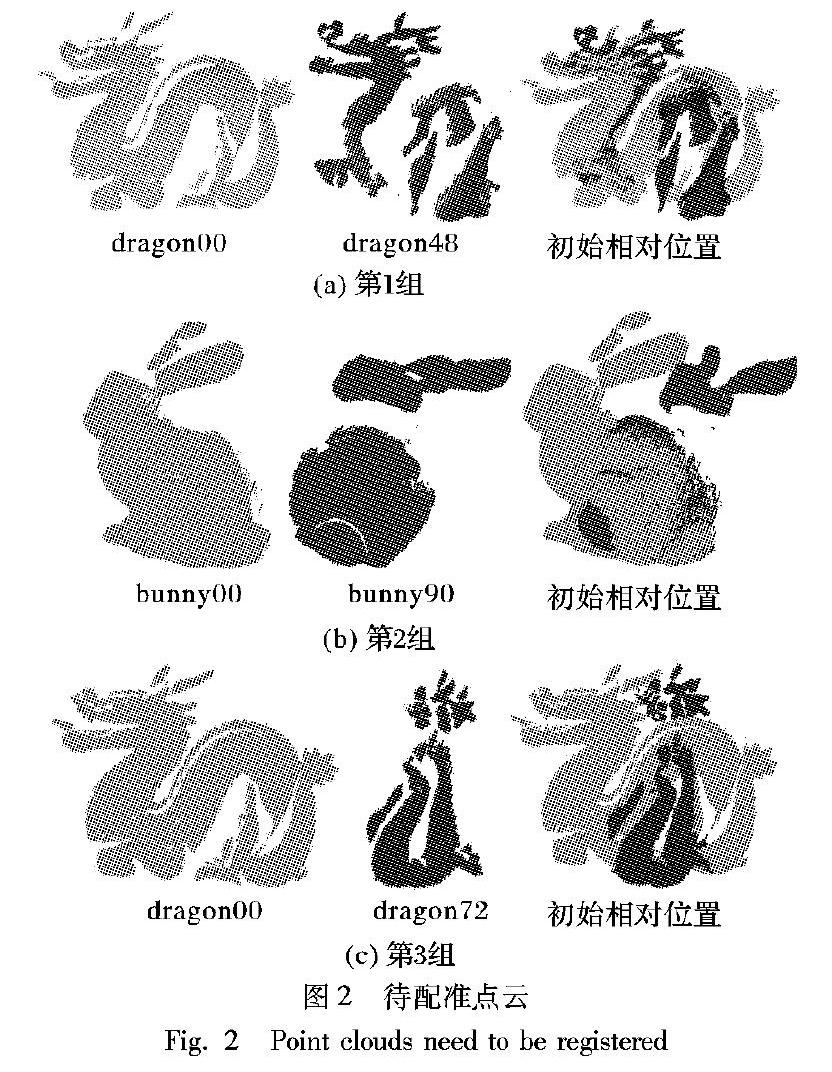
待配准的三组公共点云数据模型分别如图2所示，每组点云的覆盖率均低于60%，并且第2组点云的覆盖率低于第1组，第3组点云的覆盖率又低于第2组。采用本文所提的基于区域分割的点云配准算法，首先提取点云的凹凸特征点，然后对特征点进行区域分割，最后对区域进行两两配准，从而实现点云模型的配准。公共点云的最终配准结果如图3所示，显然，该基于区域分割的点云配准算法可以实现公共点云的准确配准。

为了进一步验证所提区域分割配准算法在配准精度和耗时等方面的性能，针对图2三组公共点云，再分别采用ICP算法、文献[19]算法、文献[20]算法和文献[13]算法进行配准，五种算法的配准结果如表1所示。

从表1可见，该基于区域分割的配准算法最有最高的配准精度和最快的配准速度。與ICP算法相比，基于区域分割的配准算法的配准精度和速度分别提高了约35%和50%;与文献[19]算法相比，基于区域分割的配准算法的配准精度和速度分别提高了约25%和38%;与文献[20]算法相比，基于区域分割的配准算法的配准精度和速度分别提高了23%和35%;与文献[13]算法相比，基于区域分割的配准算法的配准精度和速度分别提高了约12%和22%。这是由于：ICP 算法对点云的初始相对位置要求较高，且要求待配准点云之间存在包含关系;文献[19]算法是一种基于迭代因子的点云配准算法，该迭代因子可以提高点云配准的迭代速度，但是不能提高低覆盖率点云的配准精度;文献[20]算法是一种基于内部形态描述子（Intrinsic Shape Signature， ISS）特征点的点云配准算法，该算法通过对点云上特征点的特征序列的匹配来实现点云配准，取得了较精确的匹配结果，但是对覆盖率低于60%的点云配准效果不佳;文献[13]算法是一种基于X射线断层扫描的点云配准算法，通过基于距离误差评价的ICP 算法实现了点云配准，但是该算法对密度较高点云的配准效果较好，对低覆盖点云配准效果不佳。而基于区域分割的配准算法通过区域分割有效避免了低覆盖区域对点云配准的影响，可以实现点云的快速精确配准。

4.2 文物断裂面匹配

本文基于区域分割的点云配准算法可以用于文物碎块点云数据模型的断裂面匹配，首先采用文献[21]算法提取碎块的断裂面，然后采用该配准算法将断裂面进行匹配。4组待匹配文物碎块如图4所示，碎块的点云数据大小、原始面数目和断裂面数目如表2所示，采用该基于区域分割的点云配准算法对碎块断裂面进行匹配的结果如图5所示。从图5可见，该点云配准算法可以实现文物碎块断裂面的有效配准。

为了进一步验证所提配准算法在配准精度和耗时等方面的性能，针对图4所示的四组文物碎块数据模型，再分别采用ICP算法、文献[19]算法、文献[20]算法和文献[13]算法对其断裂面进行匹配，五种算法的匹配结果如表3所示。表3中的匹配误差是指可以正确匹配的两个断裂面的匹配误差，耗时是指可以正确匹配的两个断裂面的匹配耗时。

从表3可见，本文基于区域分割的点云配准算法最有最高的匹配精度和最快的匹配速度。与ICP算法相比，区域分割配准算法的匹配精度和速度分别提高了约35%和50%;与文献[19]算法相比，区域分割配准算法的匹配精度和速度分别提高了约24%和37%;与文献[20]算法相比，区域分割配准算法的匹配精度和速度分别提高了约22%和35%;与文献[13]算法相比，区域分割配准算法的匹配精度和速度分别提高了约13%和23%。

这是由于：ICP 算法对点云的初始相对位置要求较高，且要求待配准点云之间存在包含关系，因此对文物碎块断裂面的匹配效果不佳;文献[19]算法虽然可以通过动态调整迭代因子提高算法的收敛速度，但是对低覆点云的配准效果不佳，而文物碎块断裂面大多存在缺损，覆盖率较低，因此匹配误差较大;文献[20]算法通过提取ISS特征点的实现点云配准，但是由于是对文物碎块的整个断裂面进行特征点提取，因此对缺损文物的断裂面匹配效果不佳;文献[13]算法采用基于距离误差评价的ICP 算法实现了破损砂粒断裂面的匹配，但算法是非特征提取算法，不利于缺损文物碎块粗糙断裂面的匹配;而提出的基于区域分割的点云配准算法通过区域分割有效避免了低覆盖区域对断裂面匹配的影响，可以实现文物碎块断裂面的有效匹配。

综上，所提基于区域分割的点云配准算法不仅适用于公共点云数据模型的配准，而且对文物类刚体文物碎块的断裂面匹配效果良好。因此说，所提配准算法是一种快速、高精度的低覆盖率点云模型配准算法。

5 结语

点云配准研究已久，其应用领域涉及工业设计、医学研究、颅面复原以及文物修复等诸多方面。本文针对低覆盖率的点云数据模型，提出一种基于区域分割的点云配准算法。该算法通过对点云模型上的特征点进行区域划分，不仅大幅降低了点云配准的规模，而且有效提高了配准区域的覆盖率，从而提高了点云配准的时间效率和配准精度。但是本文算法所用的数据模型均为低噪声的采样均匀的点云数据模型，算法并未考虑大量噪声对点云配准结果的影响。在今后的研究中，要进一步考虑噪声和点云密度对点云配准的影响，提出更加普适性的点云配准算法，以提高点云配准算法的应用范围。

参考文献 （References）

[1]郭延杰，白福忠，张铁英，等. 基于 Radon 变换与灰度重心法的环形目标直径测量方法[J]. 激光与光电子学进展， 2015， 52（8）：209-213. （GUO Y J， BAI F Z， ZHANG T Y， et al. Ring object diameter measuring method based on Radon transform and gray gravity algorithm[J]. Laser and Optoelectronics Progress， 2015， 52（8）：209-213.）

[2]馮筠，陈雨，仝鑫龙，等. 三维颅骨特征点的自动标定[J]. 光学精密工程， 2014， 22（5）：1388-1394. （FENG J， CHEN Y， TONG X L， et al. Automatic feature point extraction for threedimensional skull[J]. Optics and Precision Engineering， 2014， 22（5）：1388-1394.）

[3]张琮毅，魏子庄，徐昊文，等. 尺度可变的快速全局点云配准方法[J]. 计算机学报， 2019， 42（9）：1939-1952. （ZHANG Z Y， WEI Z Z， XU H W， et al. Scale variable fast global point cloud registration[J]. Chinese Journal of Computers， 2019， 42（9） ：1939-1952.）

[4]蔺素珍，王栋娟，钟家让，等. 利用曲率特征虚拟拼接青铜器小碎块的方法[J]. 西安电子科技大学学报（自然科学版）， 2016， 43（6）： 141-146. （LIN S Z， WANG D J， ZHONG J R， et al. Approach to reassembling virtual small bronze fragments using the curvature feature[J]. Journal of Xidian University （Natural Science）， 2016， 43（6）： 141-146.）

[5]BESL P J， MCKAY N D. A method for registration of 3D shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1992， 14（2）：239-256.

[6]DU S， LIU J， ZHANG C. Probability iterative closest point algorithm for mD point set registration with noise[J]. Neurocomputing， 2015， 157：187-198.

[7]LI S， LEE D. Fast Visual odometry using intensityassisted iterative closest point[J]. IEEE Robotics and Automation Letters， 2016， 1（2）： 992-999.

[8]MARANI R， REN V， NITTI M， et al. A modified iterative closest point algorithm for 3D point cloud registration[J]. ComputerAided Civil and Infrastructure Engineering， 2016， 31（7）： 515-534.

[9]LAMINE TAZIR M， GOKHOOL T， CHECCHIN P， et al. CICP： Cluster iterative closest point for sparsedense point cloud registration[J]. Robotics and Autonomous Systems， 2018，108：66-86.

[10]邵红旭. 低重叠率点云配准技术研究[D]. 哈尔滨： 哈尔滨工程大学， 2018：43-45. （SHAO H X. Research on point cloud registration technology with small overlap[D]. Harbin： Harbin Engineering University， 2018：43-45.）

[11]XU H， CHEN G， WANG Z， et al. RGBDbased pose estimation of workpieces with semantic segmentation and point cloud registration[J]. Sensors， 2019， 19（8）： No.1873.

[12]DING J， LIU Q， SUN P. A robust registration algorithm of point clouds based on adaptive distance function for surface inspection[J]. Measurement Science and Technology， 2019， 30（7）： No. 075003.

[13]WU M， WANG J. Registration of point cloud data for matching crushed sand particles[J]. Powder Technology， 2019， 347：227-242.

[14]LIU S， GAO D， WANG P， et al. A depthbased weighted point cloud registration for indoor scene[J]. Sensors， 2018， 18（11）：No.3608.

[15]王帅，孙华燕，郭惠超. 适用于激光点云配准的重叠区域提取方法[J]. 红外与激光工程， 2017， 46（S1）： 137-142. （WANG S， SUN H Y， GUO H C. Overlapping region extraction method for laser point clouds registration[J]. Infrared and Laser Engineering， 2017， 46（S1）： 137-142.）

[16]巢淵，戴敏，陈恺，等. 基于广义反向粒子群与引力搜索混合算法的多阈值图像分割[J]. 光学精密工程， 2015， 23（3）：879-886. （CHAO Y， DAI M， CHEN K， et al. Image segmentation of multilevel threshold using hybrid PSOGSA with generalized oppositionbased learning[J]. Optics and Precision Engineering， 2015， 23（3）：879-886.）

[17]夏棒， EMILION R，王惠文. Dirichlet 混合样本的 EM 算法与动态聚类算法比较[J]. 北京航空航天大学学报， 2019， 45（9）：1805-1811.（XIA B， EMILION R， WANG H W. A comparison between EM algorithm and dynamical clustering for Dirichlet mixture samples[J]. Journal of Beijing University of Aeronautics and Astronautics， 2019， 45（9）：1805-1811.）

[18]WU Z， LEAHY R. An optimal graph theoretic approach to data clustering： theory and its application to image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1993， 15（11）：1101-1113.

[19]朱丽品，刘晓宁，刘雄乐，等. 加入迭代因子的层次化颅骨配准方法[J]. 中国图象图形学报， 2017， 22（4）： 523-531. （ZHU L P， LIU X N， LIU X L， et al. Hierarchical skull registration method with an iterative factor[J]. Journal of Image and Graphics， 2017， 22（4）： 523-531.）

[20]赵夫群，耿国华. 基于特征点的秦俑断裂面匹配方法[J]. 激光与光电子学进展， 2018，55（4）： 122-128. （ZHAO F Q， GENG G H. Fracture surface matching method for Terracotta based on feature points[J]. Laser and Optoelectronics Progress， 2018，55（4）： 122-128.）

[21]李群辉，周明全，耿国华. 破碎刚体三角网格模型的断裂面分割[J]. 计算机应用， 2011， 31（8）：2204-2206， 2216. （LI Q H， ZHOU M Q， GENG G H. Fractured surface segmentation of triangular mesh of fragments for solid reconstruction[J]. Journal of Computer Applications， 2011， 31（8）： 2204-2206， 2216.）

This work is partially supported by the National Natural Science Foundation of China （61673319， 61731015）， the Major Special Project of Independent Innovation in Qingdao （2017-4-3-2xcl）， the Special Project of Scientific Research Program of Shaanxi Education Department （19JK0842）.

TANG Hui， born in 1982， Ph. D. candidate， experimentalist. Her research interests include graphics and image processing.

ZHOU Mingquan， born in 1954， M. S.， professor. His research interests include computer visualization， software engineering， Chinese information processing.

GENG Guohua， born in 1955， Ph. D.， professor. Her research interests include graphics and image processing，threedimensional reconstruction.