图的全着色研究综述
2019-12-23
(广州大学 计算科技研究院, 广东 广州 510006)
1 引 言
图的点着色和边着色是图论主要的研究方向,这些问题不仅在理论上具有重要的研究意义,在现实生活中也具有广泛的应用[1-2].在点着色和边着色的基础上,学者们又提出了全着色的概念.本文主要对图的全着色研究进展进行综述.首先给出文中采用的一些基本定义和符号,如果有未说明的,可参见文献[3].
在没有特殊声明的情况下,本文所言之图都指简单无向图.对于给定图G,分别用V(G)和E(G)表示G的顶点集和边集.图G中所含的顶点数和边数分别称为G的阶和规模.若G的规模为0,即E(G)=∅,则称G为空图.两个顶点u,v∈V(G) (或两条边e1,e2∈E(G))称为相邻的如果uv∈E(G) (或e1,e2具有相同的端点).G中的顶点u和边e称为是关联的如果u是e的一个端点.用NG(u)表示G中与顶点u相邻的所有顶点的集合,并把|NG(u)|称为u的度数,记为dG(u).分别用δ(G)和Δ(G)表示G的最小度和最大度.所有顶点度数都为G的图称为k-正则图,通常3-正则图称为立方图.
给定图G,若V(G)中任意两个顶点在G中都相邻,则称图G为完全图,本文用记号Kn表示n-阶完全图.可见,完全图是与空图相对的另一个极端情况.如果V(G)可以被划分成k个互不相交的子集(称为部分)V1,V2,…,Vk, 即对于任意i,j∈{1,2,…,k},i≠j,Vi∩Vj=∅且V=V1∪V2∪…∪Vk,使得任一边e的两个端点不在同一个子集中,那么称G为k-部图.如果一个k-部图的任意两个不属于同一部分的顶点都相邻,那么称其为完全k-部图,用K(r1,r2,…,rk)表示k个部分分别含有r1,r2,…,rk个顶点的完全k-部图.如果一个k-部图的每个部分所含的顶点数都相同,则称其为等k-部图.2-部图也称为偶图(或二部图),一般用G[V1,V2]表示具有部分V1,V2的二部图;特别地,用Km,n表示两个部分分别含有m和n个顶点的完全二部图.把K1,n称为星,用Sn表示.
一个图H称为是G的子图如果V(H)⊆V(G)并且E(H)⊆E(G).令H是G的一个子图,如果V(H)=V(G),那么称H是G的生成子图;如果对于u,v∈V(H),u,v在G中相邻当且仅当它们在图H中相邻,则称H为G的导出子图,或由V(H)导出的子图,记为G[V(H)].令U是图G的一个顶点子集,如果U中任意两个顶点在G中都相邻,那么称U为G的一个团;如果U中任意两个顶点在G中都不相邻,那么称U为G的一个独立集.
一个图称为路如果该图的所有点和边可以排列成一个点边序列v1e1v2e2…vn-1en-1vn使得ei=vivi+1,i=1,2,…,n-1,并且序列中不含相同的点和相同的边;如果在路v1e1v2e2…vn-1en-1vn的基础上添加一条边v1vn,所得之图称为圈.路和圈中所含的边数称为它们的长度.本文用Pn=v1v2…vn-1vn和Cn=v1v2…vn-1vnv1分别表示长度为n-1的路和长度为n的圈.长度为n的圈称为n-圈,3-圈称为三角形.不含圈的连通图称为树.两个圈称为是相交的如果它们顶点集的交不空,两个圈称为是相邻的如果它们边集的交不空.
图G的一个k-全着色是指从V(G)∪E(G)到颜色集{1,2,…,k}的一个映射f,满足下面3个约束条件:
(1)对于任意u,v∈V(G),如果u,v相邻,则f(u)≠f(v);
(2)对于任意e1,e2∈E(G),如果e1与e2相邻,则f(e1)≠f(e2);
(3)对于任意u∈V(G),e∈E(G),如果u与e关联,则f(u)≠f(e).
如果图G含有一个k-全着色,那么称G是k-可全着色的.把使得G是k-可全着色的最小的正整数k称为G的全色数,表示为T(G).很显然,T(G)≥Δ(G)+1.关于图的全色数,Vizing[4]和Behzad[5-6]分别独立提出下述猜想.
猜想1.1(全着色猜想TCC) 对任意简单图G,有
T(G)≤Δ(G)+2.
实际上,Vizing[4]所提的猜想是针对多重图的,故更具一般性,他所提形式为:对于任意图G,T(G)≤Δ(G)+μ(G)+1,其中μ(G)表示G的重数(若G是简单图,其重数为1).由于本文只关注简单图,故对多重图全着色的研究不做过多介绍.
虽然在20世纪70年代,国内外许多学者已经证明了TCC对一些特殊图类成立,但到目前为止还没有给出其一个完整的证明,其难度可见一斑.为了解决TCC,图论届的学者们相继提出了多种方法去攻克它,业已得到了许多非常漂亮的结果.目前,对于最大度不超过5的图,已经证明了TCC成立[7-9].对于度数大的图,Molly等[10]利用概率方法(Lovász 局部引理)证明了当Δ(G)足够大时,T(G)≤Δ(G)+1026.该结论虽然具有一般性,但是与TCC相差甚远,所以用该方法并不能解决TCC.对于平面图来说,利用放电法寻找可约的不可避免构型的策略,已经证明了对于最大度不为6的所有平面图TCC成立.不过,人们还是想利用此方法把最大度为6的情况也解决,但是对于此情况,如何设计放电规则来寻找可约的不可避免集是一件非常困难的工作.
关于全着色问题的研究主要可归为四个方面:①探讨具有一定限制条件的图的全色数;②探讨基于全色数的图的分类;③证明TCC对于平面图成立;④图的全着色算法和计算复杂性方面的研究.张忠辅等[11]在1992年对图的全着色研究进展进行了综述,介绍了1991年之前的和一些待发表的相关研究成果,并列出了一些当时尚未解决的问题.1996年,Yap[12]对全着色的研究进行了进一步的总结,介绍了1995年之前的关于全着色的一些研究成果.2013年,Borodin在文献[13](5.3节)中简短地介绍了2009年之前的平面图全着色的研究情况.最近,Geetha等[14]又在上述综述的基础上,添加了一些近年来的关于全着色的研究成果.本文参考上述文献,对全着色的研究进行全面探讨,综述从1964年以来尽可能多的研究成果,并分析文献中所使用的求解方法,为感兴趣的读者提供参考.
2 具有限制条件图的全着色
由于一般图的全色数很难判定,所以人们转向研究了具有限制条件图的全着色,包括一些特殊图类,度数有限制的图,运算图等等.本节主要介绍一些满足TCC的图类,即全色数小于等于最大度加2的图类,对于已经得到全色数精确值的图类将在第3节给予详细介绍.
2.1 特殊图类
下面介绍几类满足TCC的图类,这些图类不是很常见,但它们的结构都具有一定的规律可循.
定义2.1(Unitary Cayley图)Unitary Cayley图是定义在环R上的图GR,它的顶点集V(GR)=R,即R中的每个元素对应GR中的一个顶点,边集E(GR)={i,j∈R,i-j与R中所含的元素数互质}[15].文献[14](定理3.1)证明了TCC对于Unitary Cayley图成立.
定理2.1[14]令G是Unitary Cayley图,则T(G)≤Δ(G)+2.
由于Unitary Cayley图包含完全图和完全多部图,所以由定理2.1也可以推出TCC对完全图和完全多部图成立.
定义2.2(Mock Threshold图)对于任意n-阶图G,如果G的顶点可以排成一个序列v1,v2,…,vn使得对于任意i∈{1,2,…,n},v1,v2,…,vi中每个顶点的度数属于0,1,i-1,i-2中的一个,那么称G是Mork Threshold图.文献[14](定理3.2)证明了此类图满足TCC.
定理2.2[14]令G是Mork Threshold图,则T(G)≤Δ(G)+2.

为了构建具有大的色数但是具有小的团数的图,1955年,Mycieski[16]引入了Mycielskian. 2003年,Lam等[17]将Mycielski图进行了扩展,构造了广义Mycielski图并研究了此类图的循环色数.关于广义Mycielski图的研究有很多,作者在2017年研究了此类图的邻点可区别全色数[18].
2014年,Chen等[19]证明了TCC对于广义Mycielski图成立.
定理2.3[19]对于任意n-阶图G和任意正整数m,有T(μm(G)≤Δ(μm(G))+2;特别地,当Δ(G)≤(n-1)/2或G是完全图且n≥3时,有T(μm(G))=Δ(G)+1.
定义2.4(奇图)对于正整数n,n-阶奇图On定义如下:On的每个顶点对应含有2n-1个元素的集合的一个(n-1)-元子集,两个顶点相邻当且仅当它们对应的子集不交.文献[14]证明了TCC对于此类图成立.
定理2.4[14]令On是n-阶奇图,则T(On)≤Δ(On)+2.
2.2 低度图和高度图
2.2.1 低度图
对于低度图,目前TCC被证明仅对最大度不超过5的图成立,而且这些结论都是在20世纪90年代以前得到的.可以说对于一般图的全着色,近20年来几乎没有太大的进展.对于最大度不超过3的图,1971年Rosenfeld[7]和Vijayditya[20]分别独立地证明了TCC成立.
定理2.5[7,20]设G是最大度不超过3的图,则T(G)≤Δ(G)+2.
证明定理2.5是全着色领域开创性的工作,其证明思路如下:
令G是最大度不超过3的连通图,实际上只需考虑不含割边的3-正则图即可.因为若G含有割边或含度数小于等于2的顶点,那么对G的顶点应用数学归纳法,很容易证明TCC成立.对于不含割边的3-正则图G,给G的顶点正常4-着色,记为f.由于不含割边的3-正则图可以分解成边不交的圈的并和一个完美匹配(Petersen定理[21],见文献[3]定理16.14),所以G可被分解成边不交的圈C1,C2,…的并和一个完美匹配F. 又因为f可以被扩展成G-F的一个4-全染色,所以在此基础上,给F中的边都着颜色5即得到G的一个5-全着色,从而证明了TCC对最大度不超过3的图成立.
在上述工作的基础上,Kostochka研究了多重图的全色数,证明了TCC对最大度为4和5的多重图成立.对于最大度为4的图,Kostochka在1977年证明了下述结论.
定理2.6[8]对任意最大度为4的多重图G,有T(G)≤6.
证明关于定理2.6的证明,只需考虑G是4-正则时的情况,这是因为任何一个最大度为Δ的图都可以被嵌入到一个Δ-正则图中.由于任意2n-正则多重图,n≥1,都是2-可因子分解的[21](见文献[12]引理4.7),所以4-正则图G可以分解成2个边不交的2-因子F1,F2的并. 首先给图G正常4-顶点着色(Brooks定理),记为f. 容易证明f可以扩展成F1的一个正常4-全染色.对于F2中的奇圈C1,C2,…,可以在每个奇圈上取一个顶点v1,v2,…使得在f下,|f(ui)∪A(vi)∪A(ui)|≤3且v1,v2,…在F1中不形成奇圈,其中ui是vi在Ci中的邻点,A(vi)={f(e)|e=xvi∈E(F1)}. 这样通过给v1,v2,…重新用另外两种色进行正常2-着色之后,C1,C2,…中的边就可以正常着色了,故定理得证.
关于最大度为5的图,1978年Kostochka[22]在他的博士论文中证明了对于最大度为5的多重图TCC成立,但是由于篇幅较长,并没见发表.直到1996年,Kostochka[9]又给出了一个相对较短的证明.
定理2.7[9]对任意最大度为5的多重图G,有T(G)≤7.
2.2.2 高度图
在20世纪70年代,人们证明了TCC对于低度图成立(最大度小于6的图),但是后来很难再取得进展,故到90年代前后,学者们开始研究高度图的情况.
1987年,王建方等[23]通过设计一些变换,可以通过扩展一个(n-1)-阶完全图的全着色获得最大度为n-2的n-阶图的一个n-全着色,从而证明了TCC对于最大度大于等于|V(G)|-2的图G成立.
定理2.8[23]对于n-阶图G,如果Δ(G)≥n-2,则T(G)≤Δ(G)+2.
该成果引起了人们研究TCC对高度图成立的热情.1989年,Yap等[24]对其进行了改进,他们首先在一个图的基础上添加一个新的顶点,然后通过扩展新图的边着色来得到原图的一个全着色.基于此方法,他们证明了TCC对于最大度大于等于|V(G)|-4的图G成立.1992年,Yap等[25]又进一步将上述结论改进到|V(G)|-5.
定理2.9[25]对于n-阶图G,如果Δ(G)≥n-5,则T(G)≤Δ(G)+2.
1993年,Hilton等[26]进一步证明了TCC对于最大度大于等于3|V(G)|/4的图成立.
定理2.10[26]对于n-阶图G,如果Δ(G)≥3n/4,则T(G)≤Δ(G)+2.
2003年,Xie等[27]研究了阶数为偶数的高度图的全色数,证明了TCC对于满足Δ(G)+δ(G)≥3|V(G)|/2-5/2的偶阶图G成立.另外,对于偶阶正则图,在文献[28]中,Xie等证明了TCC对于满足k≥2n/3+23/6的n-阶k-正则图G成立,其中n是偶数.2009年,Xie等[29]又进一步将此结论扩展到了一般正则图上,得到下述定理.
定理2.11[29]对于n-阶k-正则图G,如果k≥2n/3+23/6,那么T(G)≤Δ(G)+2.
由于TCC若对于k-正则图成立,那么TCC对于所有最大度为k的图都成立[30],所以上述对于正则图成立的结论对于具有相同最大度的非正则图也成立.这也说明,证明TCC成立只需探讨正则图即可.
2.3 全色数的若干上界
除了上述从低度图和高度图两个方面研究TCC外,还有学者试图通过放宽TCC中界的方法来研究TCC.1977年,Kostochka[8]证明了对于大部分最大度大于等于6的图G,T(G)≤3Δ(G)/2.1985年,Bollobás等[31]通过列表边着色的方法证明了如果一个图的最大度足够大时,该图的全色数存在一个不超过2倍最大度的上界.
定理2.12[31]令常数c满足11/6 1991年,Chetwynd等[32]研究了高密度图的全色数的界,他们证明了如下定理. 定理2.13[32]如果一个图G的最小度δ(G)≥3|V(G)|/4,那么T(G)≤Δ(G)+3;特别地,如果δ(G)≥5(|V(G)|+1)/6,那么T(G)≤Δ(G)+2. 1990年,Hint[33]通过研究边色数(用′(G)表示图G的边色数)和点色数(用(G)表示图G的点色数)与全色数之间的关系,得到了下面的上界. 定理2.14[Hind定理][33]对于任意图G,有T(G)≤ 定理2.15[33]对于任意图G和任意正整数k≤Δ(G),有T(G)≤′(G)+「(G)/k⎤+k. 文献[34]中,作者改进了Hind定理的上界,他们利用概率方法(Erdos-Lovász局部引理)证明了任意点色数为k的图的全色数至多比其边色数多18k1/3log1/23k. 1992年,Hind[35]又得到一个关于最大度的上界. 定理2.16[35]对于任意n-阶图G,有T(G)≤Δ(G)+2「n/Δ(G)⎤+1. 1992年,Häggkrist等[36]证明了图的全色数不超过其边色数和一个常数的和. 定理2.17[36]对于n-阶图G若k是满足k!>n的最小正整数,那么T(G)≤′(G)+k. 实际上,文献[37]中证明了比定理2.17稍弱的一个结论(对于n-阶图G和任意正整数k. 若k!≥n,则T(G)≤′(G)+k+1). 另外,当n和最大度都很大的时候,定理2.17的界要好于定理2.15. 文献[38]中,McDiarmid等证明了另一个关于最大度的界. 定理2.18[38]对于任意图G,则T(G)≤7Δ(G)/5+3. 1995年,Sánchez-Arroyo[39]改进了定理2.18的结论,他证明了如下定理. 定理2.19[39]对于任意图G,有T(G)≤′(G)+⎣(G)/3」+2. 定理2.20[40]对于任意n-阶图G,有 n+1≤T(G)+ 进一步,他证明了当n是任意奇数时,这些界都可达. 1987年,王建方等[41]进一步研究了图与补图的全色数,改进了Cook的结论. 定理2.21[41]对于任意n-阶图G,有 n+1≤T(G)+ 尽管目前已经获得许多全色数的上界,但是都与TCC相差甚远,所以通过逼近上界的方法来证明TCC成立似乎不太可行. 基于全色数,可以将图G分成两类.如果T(G)=Δ(G)+1,则称G是第一类图;如果T(G)=Δ(G)+2,则称G是第二类图.本节着重对这两类图进行介绍. 在TCC提出的早期,学者们为了验证其正确性,探讨了一些特殊图类的全色数.对于至少含有3个顶点的树来说,通过数学归纳法,很容易证明其全色数是Δ+1,即树是第一类图.对于n-圈Cn,n≥3,显然T(Cn)≥3.当n≡0(mod 3)时,容易给出Cn的3-全着色,所以T(Cn)=3,即n≡0(mod 3)时Cn是第一类图.另外,由于在Cn的任意3-全着色下,连续的3条边必着3种不同的颜色,所以n≢0(mod 3)时可以推出T(Cn)=4,即n≢0(mod3)时Cn是第二类图. 1967年,Behzad等[42]精确地刻画了完全图和完全二部图的全色数. 定理3.1[42]对于n-阶完全图Kn,当n是奇数时,T(Kn)=n;当n是偶数时,T(Kn)=n+1. 证明定理3.1的证明并不复杂.当n是奇数时,它的一个n-全着色可以通过如下规则给出.令V(Kn)={v0,v1,…,vn-1},定义Kn的一个n-全着色f如下:对于每个i∈{0,1,2,…,n-1},令f(vi)=f(vi+jvi-j)=i+1,其中对于每个i,下标j都取遍所有的{1,2,…,⎣n/2」},并且下标取模n. 当n是偶数时,可以加一个新的顶点并让其连接Kn中的所有顶点,从而得到完全图Kn+1.这样,通过上述方法,可以得到Kn+1的一个(n+1)-全着色f1.显然f1限制在Kn上的着色既是Kn的一个(n+1)-全着色.上述说明当n是奇数时,T(Kn)≤n;当n是偶数时,T(Kn)≤n+1.注意到,T(Kn)≥Δ(Kn)+1=n. 所以,当n是奇数时,T(Kn)=n.另外,当n是偶数时,Kn共有n个顶点,n(n-1)/2条边.如果此时T(Kn)=n,由鸽巢原理,至少有一种颜色需要着至少「(n+1)/2⎤多个元素.但是当n是偶数时,Kn中的独立元素(包括点和边)最多有n/2个,故矛盾!所以,此时T(Kn)=n+1. 上述通过鸽巢原理证明全色数下界是基本的证明思路,但并不是对所有图都可行,所以在实际研究中,可以将其与其它策略相结合来进行探索. 定理3.1说明当n是奇数时完全图Kn是第一类图,否则是第二类图. 对于一般的二部图G,因为任意二部图的边色数不超过该图的最大度(见文献[3],定理17.2),所以有T(G)≤Δ(G)+2,即TCC对于二部图成立.对于完全二部图,Behzad等[42]证明了下述结论. 定理3.2[42]对于完全二部图Km,n,有T(Km,n)=max(m,n)+1+δm,n,其中δm,n=0若m≠n,否则δm,n=1. 由定理3.2知,当m≠n时,Km,n是第一类图;当n=m时,Km,n是第二类图.Chen等[43]研究了Kn,n删除一些边后的图是第一类图的充要条件,他们证明了(n-2)-正则等二部图Kn,n-E(J)是第一类图当且仅当J含有长度为4的圈C4,其中J是Kn,n的子图,Kn,n-E(J)表示从Kn,n中删除属于J中的边.Hilton[44]证明了Kn,n-E(J)是第二类图当且仅当|E(J)|+α′≤n-1,其中α′表示J中最大匹配所含的边数.2005年,Campos等[45]研究了一些具有特定结构的二部图是第一类图的充分条件,包括网格图,近梯形图,k-立方体. 对于完全k-部图,k≥3,Rosenfeld[7]在1971年研究了完全三部图和完全等部图的全着色,他证明了TCC对于这两类图成立.该结论在1989年被Yap[46]扩展到所有完全k-部图,他通过证明TCC对含有至少|V(G)|-Δ(G)-1个点的独立集的图G成立[24],证明了TCC对所有完全k-部图成立. 定理3.3[46]对于任意正整数k,完全k-部图G的全色数满足T(G)≤Δ(G)+2. 由于奇阶完全图是第一类图,很自然联想到:是否奇阶完全多部图也是第一类图?1992年,Chew等[47]研究了此问题,并证明了奇阶完全多部图是第一类图. 定理3.4[47]奇阶完全k-部图是第一类图. 在定理3.4的证明过程中[47],他们还证明了当r1 关于判断偶阶完全多部图是第一类图的条件,直到2000年才有了一些进展.Dong等[48]在2000年证明了对于偶阶完全k-部图K(r1,r2,…,rk),r1≤r2≤…≤rk,如果r2≤r3-2,那么该图是第一类图;同时他们还证明了若K(r1,r2,…,rk)不是正则的且k=4,那么K(r1,r2,…,rk)也是第一类图.这些定理的证明技巧大多是通过先把问题分解成若干种情况,然后再逐个攻克其中困难的情况.证明过程主要基于Hoffman等[49]提出的对顶点的着色思想:给某一部分的顶点都着相同的颜色,同时所有其它的顶点着不同的颜色. 近年来,Dalal等[50-51]利用图合并技术[52],研究了具有较低def(G)的完全多部图G的全色数,其中def(G)被称为图G的deficiency,定义为 def(G)=∑v∈V(G)(Δ(G)-dG(v)), 可见def(G)可以用来衡量图G与正则图之间的相差程度.在文献[50]中,Dalal研究了完全5-部图的全色数,证明了K(r1,r2,…,r5)是第二类图的充要条件是K(r1,r2,…,r5)的阶数是偶数并且def(K(r1,r2,…,r5))小于图中含有奇数个顶点的部分数.在文献[51]中,作者给出了一个判断偶阶完全k-部图K(r1,r2,…,rk)是第一类图的充分条件,改进了Dong等[48]的结论. 定理3.5[51]对于偶阶完全k-部图K(r1,r2,…,rk),r1≤r2≤…≤rk,k>2,如果r2 在文献[51]中,Dalal改进了文献[50]中的结论,他证明了偶阶完全k-部图K(r1,r2,…,rk)是第二类图当且仅当def(K(r1,r2,…,rk))小于K(r1,r2,…,rk)中含有奇数个顶点的部分数.此外,一个特定形式的偶阶完全k-部图的全色数被完全刻画:K(r,r,…,r,r+1)是第一类图的充要条件是r≥k-2. 对于任意n-阶图G,若n是奇数并且Δ(G)=n-1,这时G一定是第一类图,因为任意奇阶完全图是第一类图.为此,研究图的分类最先的目标是探讨n是偶数并且Δ(G)=n-1的情况,关于这方面的先驱工作可以归宿到1990年,Hilton[53]证明了下述定理. 定理3.6[53]令H是2n-阶完全图K2n的一个子图,n≥1,则T(K2n-E(H))=2n+1的充要条件是|E(H)|+h≤n-1,其中h表示H中最大匹配(任意两条边都不相邻的边集)所含的边数. 按定理3.6中的条件,显然K2n-E(H)是最大度为2n-1的2n-阶图.由于H具有任意性,上述条件可以作为判断最大度为2n-1的2n-阶图是第一类图的充要条件,即 定理3.7[12]令G是最大度为2n-1的2n-阶图,则G是第一类图的充要条件是 1992年,Chen等[54]研究了最大度为2n-2的2n-阶图的全色数,他们证明了如下定理. 定理3.8[54]令G是最大度为2n-2的2n-阶图,则G是第二类图的充要条件是 对于奇阶图,Yap等[55]给出了判断最大度为2n-1的(2n+1)-阶图是第一类图的充要条件. 定理3.9[55]令G是最大度为2n-1的(2n+1)-阶图,则G是第一类图的充要条件是 对于给定图G,用GΔ表示G中所有最大度顶点的导出子图.2003年,Xie等[27]利用文献[58]中的证明技巧,通过研究GΔ的结构,证明了下述结论. 定理3.10[27]对于偶阶图G,G≠K2,如果GΔ是森林(点不交的树的并)并且δ(G)+Δ(G)≥3(|V(G)|-1)/2,那么G是第一类图. 两个图G和H的积图,通常有四种类型,包括笛卡尔积G□H,直积G×H,强积GH和字典积G∘H. 关于积图全色数的研究主要集中在笛卡尔积,对后三种积图的研究不是很多.这里统一给出这四种积图的定义. 定义3.1(积图)对于任意两个图G和H,它们上述四种积图的顶点集都是V(G)×V(H),它们的边集分别是: E(G□H)={(g,h)(g′,h′)|g=g′,hh′∈E(H) 或者h=h′,gg′∈E(G)}; E(G×H)={(g,h)(g′,h′)|gg′∈E(G)且hh′∈E(H)}; E(GH)=E(G□H)∪E(G×H); E(G∘H)={(g,h)(g′,h′)|g=g′,hh′∈E(H) 或者gg′∈E(G)}. 由定义可以看出,G□H≅H□G,G×H≅H×G,GH≅HG,但是G∘H与H∘G不一定同构.文献[59]中,作者证明了笛卡尔积图全色数与原图全色数的关系. 定理3.11[59]对于任意图G和H,如果TCC对于图G和H成立,那么TCC对于G□H也成立.特别地,如果G和H中最大度大的图是第一类图,那么G□H也是第一类图. 关于积图的全色数研究很多,主要集中于两个结构简单图的积图,比如路于路,圈与圈,完全图和完全图等等.下面对这些结论一一介绍. Seoud研究了若干笛卡尔积图的全色数.在文献[60]中,证明了对于m-阶路Pm,n-阶路Pn和n-圈Cn,Pm□Pn是第一类图(对于任意m,n),Pm□Cn是第一类图(如果n=3或n是偶数).在文献[61]中,他们证明了m-阶路Pm与(n+1)-阶星Sn的笛卡尔积图是第一类图;当n≥3时,m-阶路Cm与(n+1)-阶星Sn的笛卡尔积图是第一类图;除了P2□C5外,Pm□Cn是第一类图(该结论改进了文献[60]中相应的结论);如果n≥3并且m是偶数或者m≡0(mod 3),那么Cm□Cn是第一类图. Tong等[62]在2009年研究了圈和圈笛卡尔积图的均匀全着色(任意两种颜色着的元素数相差最多为1),他们证明了如下定理. 定理3.12[62]对于任意n,m≥3,Cm□Cn存在等5-全着色. 定理3.12说明了Cm□Cn是第一类图,该结论改进了前面Cm□Cn是第一类图的结论. 在文献[63]中,Kemnitz等探讨了两个完全图笛卡尔积图的全色数,证明了对于m-阶完全图Km和n-阶完全图Kn,如果n是奇数且n≥m,那么Kn□Km是第一类图;如果n和m都是偶数且n≥m≥4,n≡0(mod 4)或n≡6(mod 8)或n>m≥4,n≡2(mod 8),那么Kn□Km是第一类图;如果n是偶数,m是奇数,且n>(m-1)2,那么Kn□Km是第二类图.在文献[64]中,Baril等研究了积图的可区别边着色,证明了若干个(大于1个)完全图Kn(n≥2)的笛卡尔积图的邻点可区别边色数是最大度加1,其中一个图G的邻点可区别边色数是指最小的正整数k,使得G存在一个正常边着色满足任意相邻顶点具有不同的色集(出现在顶点关联边上的颜色的集合).由于图G的任意邻点(Δ(G)+1)-边着色可以扩展成该图的一个(Δ(G)+1)-全着色(只需适当地给每个顶点着一种不出现的颜色即可),所以若干个(大于1个)完全图Kn(n≥2)的笛卡尔积图是第一类图. 关于后三类积图的全着色研究,Prnaver等[65]研究了路Pn与任意图G的直积图的全色数.他们证明了如果图G是第一类图,那么TCC对于G×Pn成立;特别地,如果G的边色数是Δ(G),那么G×Pn是第一类图.此外,他们还证明了圈Cm和路Pn的直积图是第一类图.2018年,Geetha等[66]分别研究了四种积图的全着色,证明了对于任意偶数n≥4,Kn×Kn是第一类图;对于任意整数n≥3,k≥2,l≥1, 如果m=3k,5l,8l,那么,Cm×Cn是第一类图;此外,他们还证明了对于任意图H,如果TCC对K2H(K2∘H)成立,那么对于任意二部图G,TCC对于GH(G∘H)成立. 此外,还有学者研究了corona积和deleted字典积的全着色.两个图的G和H的corona积图[67],记作GH(这里为了与字典积区分,用符号‘’代替原文中的符号‘∘’),是指由一个G的拷贝和|V(G)|个H的拷贝通过将G的第i个顶点与H的第i个拷贝中的每个顶点相连边构成,其中1≤i≤|V(G)|.两个图G和H的deleted字典积图[68],记作Dlex(G,H),是指具有顶点集V(G)×V(H),边集{(g,h)(g′,h′)|gg′∈E(G)且h≠h′, 或者hh′∈E(H)且g=g′}的图.在文献[67]中,作者证明了如果TCC对于G成立,则GCn(n≥3),GKn,GKm,n和GH(H是二部图)都是第一类图.实际上,早在1992年,Seoud[60]就证明了任意两个图的corona积图是第一类图.对于deleted字典积图,Vignesh等[68]证明了如果G是二部图,H是任意满足TCC的图,那么G∘H也满足TCC;如果G的边色数是其最大度,那么对于任意至少含有3个顶点的图H,Dlex(G,H)满足TCC;特别地,如果G和H的边色数都等于它们的最大度,那么Dlex(G,H)是第一类图.最近,Vignesh等[69]又证明了如果G和H满足TCC,那么它们的点corona积图,边corona积图和邻域corona积图都是第一类图. 弦图是一类非常重要的图类,因为这类图有许多非常好的算法性质. 定义3.2(弦图)如果一个图不含长度大于3的导出圈,即每个是圈的导出子图都是三角形,那么称该图为弦图. 在第2章中,已经介绍了TCC对立方图成立.但是,讨论第一类立方图(全色数为4)的结构还是很有意义的.目前已有很多立方图类被刻画.2016年,Dantas等[73]证明了对于任意整数k>1,都存在一个整数N(k),对于所有n≥N(k),广义Petersen图G(n,k)是第一类图.该结论说明了几乎所有的广义Petersen图都是第一类图. 定义3.3(Snark)令G是不含割边的连通立方图,如果G不含3-边着色,即边色数是4(Vizing定理),那么称G为Snarks. 2003年,Cavicchiolic等[74]通过计算机辅助证明了阶数小于30的所有snarks是第一类图.他们还提出下列公开问题: 问题3.1[74]寻找(如果存在)阶数最小的全色数是5的snark. 为了解决上述问题,2011年,Campos等[75]通过递归程序为三类特殊的snarks分别构建了4-全着色,包括Flower Snarks, Goldberg Snarks和Twisted Goldberg Snarks,从而证明了这三类snarks是第一类图.基于这些结果,他们猜想所有snarks都是第一类图.2014年,Sasaki等[76]为寻找全色数是5的snarks,研究了几类特殊snarks的全色数,包括Blanuša类和一类不含四边形的snarks,然而这些snarks也都是第一类图.他们注意到对于cyclic-边连通度小于4的立方图,其全色数看似与其边色数关系不大;同时,他们还发现找到的所有第二类立方图都含有四边形.为此,他们进一步提出下列问题. 问题3.2[76]不含四边形的阶数最小的全色数为5的立方图是什么? 问题3.3[76]最小的全色数是5的snark是什么? 针对上述问题,Brinkmann等[77]在2015研究了全色数是5的snarks的构造,他们证明了对于任意不小于40的偶数n,都存在一个全色数是5的n-阶snark,从而回答了上述问题3.1和问题3.3. 另外,他们用计算机搜索验证了所有阶数不超过32的围长(最短圈的长度)为5的立方图的全色数,结果发现这些图都是第一类图.故他们提出以下三个问题. 问题3.4[77]是否存在阶数小于40的全色数是5的snark? 关于问题4,目前没有验证的仅是阶数为36和38的snarks. 问题3.5[77]最小的全色数是5的围长至少为5的立方图是什么? 问题3.6[77]是否存在g使得所有围长至少为g的立方图都是第一类图? 除了上述图类外,还有许多其它图类的全着色被研究. 定义3.4(联图)对于点不交的两个图G1,G2,若将图G1中的每个顶点与图G2中的每个顶点相连边,则得到的新图称为G1与G2的联图,对于任意n≥3,1-阶完全图K1与n-阶圈Cn的联图K1+Cn称为轮图,其中K1中的顶点称为该轮图的轮心. 定义3.5(theta图)令G是最大度为3的块,即不含割点的连通图,如果G恰好含有两个不相邻的度数为3的顶点并且其余顶点的度数都为2,那么称G为theta图. 在文献[60]中,Seoud研究了这两类图的全色数,得到下面的结论. 定理3.13[60]任意两个阶数不同的路的联图是第一类图;任意theta图是第一类图. 注意,定理3.13中构成联图的两个图要求阶数不同,如果相同结果并非如此.比如P2+P2=K4,而K4是偶阶完全图,是第二类图. 定义3.6(梯图)令C2n=u1u2…unv1v2…vnu1是长度为2n的圈,对于每个i=1,2,…,n,如果在ui和vi之间连r(≥1)条边,那么所得之图称为r重Möbius梯图,记为M2n(r).当r>1时,M2n(r)是多重图. 在文献[78]中,Chetwynd证明了如下定理. 定理3.14[78]对于任意n≥2,r≥1,M2n(r)是第二类图. 定义3.7(Compound图)两个图G和H的Compound图是指对于H中的每个顶点u,取1个G的复制Gu,并在任意两个Gv和Gw之间连一条边(或一对边)如果顶点v和w在H中相邻. 显然,不同的连边方式会产生不同的图.另外G和H的Compound图与H和G的Compound图不一定同构. 文献[79]中,Mohan等证明了如下定理. 定理3.15[79]当G和H都满足TCC时,G和H的Compound图是第一类图. 定义3.8(线图)一个图G的线图用L(G)表示,它的顶点集是G的边集E(G),两个不同的顶点e1,e2∈E(G)在L(G)中相邻当且仅当它们在G中有相同的端点. Vignesh等在文献[68]中研究了完全图Kn线图的全色数,证明了: 定理3.16[68]当n≤4时,L(Kn)是第一类图. 进一步,Vignesh等[68]猜测对于任意n,L(Kn)都是第一类图. 在文献[80]中,作者探讨了基于星和双星运算图的全色数,包括middle图,全图,线图,平方图,证明了这些图几乎都是第一类图. 定义3.9(倍图)一个图G的倍图用D(G)表示,它由G的两个拷贝组成,并对于任意uv∈E(G)在它们之间添加边(u,1)(v,2)和(v,1)(u,2),其中(x,i)表示G中的顶点x对应到其第i个拷贝中的顶点,i=1,2. 在文献[68]中,Vignesh等证明了: 定理3.17[68]如果G满足TCC,那么D(G)也满足TCC;特别地,如果G是第一类图,那么D(G)也是第一类图. 定义3.10(唯一弦)图G中圈C的一条弦是指G中不属于C的一条端点都在C上的边.圈C的一条弦称为唯一的如果C再无其它的弦. Machado和de Figueiredo[81-82]用两篇文章研究了不含唯一弦和四边形的图的全色数.他们分别证明了: 定理3.18[81-82]TCC对于不含四边形和唯一弦的图成立;特别地,对于非完全不含四边形和唯一弦的图G,当Δ(G)≥3时,G是第一类图. 定义3.11(k-退化图)对于n-阶图G,如果V(G)可以被排成一个序列,令为v1,v2,…,vn,使得每个vi都与其后面最多k个顶点相邻,k>0,那么称G是k-退化的. 关于k-退化图,1997年,Borodin等[83]证明了任意最大度Δ(G)≥2k2的k-退化图G是第一类图.2007年,Isobe等[84]改进了Borodin的结论,他们通过引入所谓的局部着色和叠加技术,利用退化图边着色的Vizing定理(最大度Δ(G)≥2k的k-退化图G的边色数等于其最大度[85-86])和二部图边着色的König定理(每个二部图的边色数等于其最大度[87])证明了: 定理3.19[84]令G是k-退化图并且Δ(G)≥k+3,则G是第一类图. 定义3.12(循环图)对于正整数序列1≤d1 Khennoufa等[88]在2008年研究了此类图的全色数,证明了此类图的参数n,k在满足一些限制条件时是第一类图. 定理3.20[88]对于任意正整数p和k<5p/2满足k≡2mod 5或者k≡3(mod 5),每个4-正则循环图C5p(1,k)是第一类图;对于任意正整数p≥3和k<3p满足k≡1(mod 3)或者k≡2(mod 3),每个4-正则循环图C6p(1,k)是第一类图. 定义3.13(Sierpiński图)对于正整数n,k及k-阶完全图Kk,Sierpiński图S(n,k)指具有顶点集{1,2,…,k}n,两个顶点u=(u1,u2,…,un)和v=(v1,v2,…,vn)相邻当且仅当存在h∈{1,2,…,n}使得下面三条成立:(1)对于所有t=1,2,…,h-1,有ut=vt;(2)uh≠vh;(3)对于t=h+1,…,n,有ut=vh并且vt=uh. 在Sierpiński图S(n,3)的基础上,收缩S(n,3)中每一条不在三角形上的边,所得之图称为Sierpiński gasket图[89],记作S(n)(这里为了与星图区别,所以用符号S(n)表示).Jakovac等[90]证明了对于任意n≥2,S(n)是第一类图;对于任意n≥1和k≥1,T(S(n,k))≤k+2;特别地,对于任意n≥1,若k≥3是奇数,则S(n,4)和S(n,k)是第一类图.对于k≥6是偶数的情况,它们猜想S(n,k)是第二类图.然而,三年之后,Hinz等[91]通过研究Hanoi图的着色,构造出了该猜想的反例,从而说明对于k≥6是偶数的情况,S(n,k)不一定全是第二类图.Geetha等[92]研究了广义的Sierpiński图S(n,G)的全色数,他们证明了对于一些特定第一类图G,比如房子图,轮图,圈的笛卡尔积图等,S(n,G)是第一类图. 本节主要介绍了一些关于第一类图和第二类图的结果,尽管目前有许多这方面的研究成果,都是局限于特定图或图类.对于一般图,很难通过这种分类方式解决TCC. 本节重点介绍平面图全着色的研究进展,首先给出平面图的定义. 定义4.1(平面图)对于图G,如果在平面上有一种G的画法使得任意两条边要么不相交要么交点是它们的公共端点,则称G是平面图或者可平面的,而这种画法称为G的一个平面嵌入.通常说平面图G均指G的一个平面嵌入. 在平面图着色领域,有一种卓越的证明技巧——放电法.该方法在图论中的应用已有百年的历史,但直到1977年,Appel等[93-94]采用该方法宣布解决四色猜想后,该方法才正式得到了广泛的关注.到目前为止,采用该方法解决的平面图着色相关的问题数不胜数,而平面图全着色的研究,也主要采用该技巧.关于放电法的详细介绍,可参见文献[95]. 由于TCC很早就被证明对于最大度小于等于5的一般图成立[9,22],当然也包括平面图,所以关于平面图全着色的结论,都是针对最大度大于等于6的平面图.1987年,Borodin[96]最早研究了平面图全着色问题,证明了TCC对于最大度大于等于11的平面图成立;两年后,他将最大度的下界从11减小到9[97].1995年,Jensen等[98]将最大度的下界减小到8(也见文献[12]).1999年,Sanders等[99]进一步将最大度的下界减小到7. 定理4.1[99]令G是最大度大于等于7的平面图,则T(G)≤Δ(G)+2. 证明在文献[99]中,作者首先定义了13种特殊类型的顶点,通过放电法证明了每个平面图至少含有它们中的1种,最后证明没有最小反例含有这些类型的点,从而产生矛盾.此外,如果承认四色定理[93-94]已经成立,定理4.1还可以证明如下[13]: 令G是一个最大度大于等于7的平面图,那么G的边色数是Δ(G)[100-101],用颜色集{1,2,…,Δ(G)}对G进行边着色,然后擦去着颜色Δ(G)-1和Δ(G)的顶点的颜色.根据四色定理,用颜色集{Δ(G)-1,Δ(G),Δ(G)+1,Δ(G)+2}对G的顶点进行着色.因为每条没有着色的边都至少有{1, 2,…,Δ(G)+1,Δ(G)+2}中两种可选的颜色,而且没着色的边在图中的导出子图是路和偶圈的并,所以这些边可以被正常着色,从而定理成立. 对于不加限制条件的平面图,定理4.1的结果是目前最好的,因为TCC对于最大度为6的平面图是否成立仍是公开的问题. 问题4.1[99]是否每个最大度为6的平面图都有8-全可着色? 关于最大度为6的平面图,尽管问题4.1还没有被彻底解决,但是已取得了大量的成果.2007年,Wang等[102]证明了: 定理4.2[102]令G是最大度为6的平面图,如果G不含4-圈,那么G是8-全可着色. 2009年,Shen等[103]改进了定理4.2的结论,证明了不含4-圈的最大度为6的平面图存在7-全着色.同年,Sun等[104]证明了不含相邻三角形的最大度为6的平面图存在8-全着色.2011年,Roussel[105]改进了Sun等[104]的结论,证明了对于最大度为6的平面图G,如果G中每个顶点v不与某个kv-圈关联,kv∈{3, 4, 5, 6, 7, 8},那么G存在8-全着色.在文献[106]中,Li又改进了Roussel的结论,证明了对于最大度为6的平面图G,如果对于任意顶点v都存在一个整数kv∈{3, 4, 5, 6}使得v不与任意kv-圈关联, 那么G存在8-全着色.2017年,作者进一步改进了Sun等[104]的结论,证明了: 定理4.3[107]令G是最大度为6的平面图,如果G不含同构于4-扇的子图,那么G存在8-全着色,其中4-扇是1-阶完全图K1与5-阶路的联图. 由于问题4.1很难被彻底解决,人们开始转向研究什么样的平面图是第一类图.在这方面,最早的研究还是源于Borodin[96],他在1987年证明了最大度大于等于16的平面图是第一类图,随后,最大度的下界分别被改进到14[97]、12[108]、11[109]和10[110],最后由Kowalik等[111]和Sun等[104]改进到9.在文献[104]中,作者还证明了不含相邻三角形并且不含长度大于等于5的圈的平面图是第一类图. 定理4.4[111]令G是最大度大于等于9的平面图,则G是第一类图. 基于定理4.4,Kowalik等[111]提出下列问题刻画第一类平面图. 问题4.2[111]使得最大度大于等于k的平面图是第一类图的最小整数k是多少? 由于K4是最大度为3的平面图且T(K4)=5,所以问题4.2中k应该属于{4,5,6,7,8,9}.基于此,Shen等[103]将上述问题改写成下述猜想: 猜想4.1[103]最大度Δ(G)满足4≤Δ(G)≤8的平面图是第一类图. 如果猜想4.1成立,那么基于定理4.4有每个最大度大于等于4的平面图都是第一类图.针对猜想4.1,对于最大度为6的平面图,Zhang等[112]证明了每个最大度至少为6的不含相邻短圈的平面图是第一类图,这里的短圈指3-圈和4-圈.Hou等[113]证明了最大度大于等于5的平面图如果不含4-圈和6-圈,那么该图是第一类图;最大度大于等于6的平面图如果不含5-圈和6-圈,那么该图是第一类图.Wu等在文献[114]中证明了平面图G如果不含弦l-圈,l=5,6,那么G有一个k-全着色,其中k=max{7,Δ(G)+1}, 这里弦l-圈指至少有一条弦的圈;注意到当Δ(G)≥6时,k=Δ(G)+1,所以此结论改进了Hou等[113]的结果. 最大度大于等于7的平面图是第一类图的充分条件包括:不含5-圈[115];对于任意顶点v都存在一个整数kv∈{3, 4, 5, 6}使得v不与任意kv-圈关联[116];3-圈不与4-圈相交或者3-圈不与长度小于6的圈相邻[117];不含相交3-圈[118];不含相交5-圈[119];不含相邻4-圈[120];不含弦6-圈[121];不含弦7-圈[122]. 对于最大度大于等于8的平面图,目前判断其是第一类图的充分条件比较多.令G是最大度为8的平面图,则G是第一类图的充分条件包括:G不含k-圈,k∈{5,6}[123];对任意顶点v∈V(G), 都存在一个整数kv∈{3, 4, 5, 6, 7, 8}使得v不与任意kv-圈关联[124];对任意顶点v∈V(G), 都存在两个整数kv,lv∈{3, 4, 5, 6, 7, 8}使得v不与相交的kv-圈和lv-圈关联[125];对任意顶点v∈V(G), 都存在两个整数kv,lv∈{3, 4, 5, 6, 7,}使得v不与相邻的kv-圈和lv-圈关联[126];G中每个7-圈至多含有两条弦[127];G不含相邻的分别含有两条弦的i-圈和j-圈,i,j∈{5, 6, 7}[128];G不含含有两条弦的5-圈[129];不含相交弦4-圈[130];每个6-圈至多含有一条弦或者任意弦6-圈不相邻[131];i-圈不与j-圈相邻,3≤i≤j≤5[132];任意v∈V(G)不关联弦6-圈或者弦7-圈或者2-弦5-圈[133];每个顶点v∈V(G)关联至多dG(v)-2⎣dG(v)/5」个三角形[134]. 在文献[135]中,Wang等研究了具有较小最大度的平面图的全着色.令G是最大度为Δ围长为g的平面图,且存在整数t>g使得G不含长度属于{g+1,…,t}的圈.他们证明了如果(Δ,g,t)∈{(5,4,6),(4,4,17)},或者Δ=3且(g,t)∈{(5,13),(6,11),(7,11),(8,10),(9,10)}且每个顶点至多关联一个长度为g的圈,那么G是第一类图. 上述这些充分条件,有些后者是前者的扩展和改进,但大多都是独立的.目前尽管得到了众多的充分条件,但是仍然没有给出第一类平面图的完全刻画,故要想解决猜想4.1,仍有大量的工作需要做.下面介绍外平面图和一些类似平面图的图类的全着色研究情况. 定义4.2(外平面图)如果一个平面图存在一种平面嵌入使得所有顶点均位于一个面(外部面)的边界上,那么称该平面图为外平面图. 文献[136]研究了外平面图的邻点可区别全着色,所得结论可以自然推广到全着色上. 定理4.5[136]令G是外平面图,如果Δ(G)≥4,那么T(G)≤Δ(G)+2;特别地,若G不含相邻的最大度点,那么T(G)=Δ(G)+1. 定义4.3(1-toroidal图)如果一个图可以画到圆环面上使得每条边与其它边相交至多一次,那么该图称为1-toroidal图. Wang[137]研究了此类图的全色数,证明了: 定理4.6[137]令G是最大度大于等于11的1-totoidal图,如果G不含相邻三角形,那么T(G)≤Δ(G)+2. 定义4.4(1-平面图)如果一个图有一个平面嵌入使得每条边至多与其它一条边交叉(不在端点处相交),那么该图称为1-平面图. Zhang等[138]研究了此类图的列表全着色,证明了对于任意1-平面图G,如果Δ(G)≥16,则G的列表全色数小于等于Δ(G)+2;如果Δ(G)≥21,则G的列表全色数等于Δ(G)+1.这也说明了1-平面图的全色数对上述结论也成立.在文献[139]中,Zhang等又进一步证明了: 定理4.7[139]令G是1-平面图,如果Δ(G)≥13,那么T(G)≤Δ(G)+2. 在文献[140]中,Czap研究了1-平面图G全色数的上界.证明了如果Δ(G)≥10,则T(G)≤Δ(G)+3;如果Δ(G)≥10且G的点色数小于等于4,那么T(G)≤Δ(G)+2;对于不含相邻三角形的1-平面图G,如果Δ(G)≥8;则T(G)≤Δ(G)+3;如果G的点色数小于等于4,那么T(G)≤Δ(G)+2. 本文对全着色的研究进展进行了全面的综述,由所阐述的结果来看,除了一些特殊的情况外,TCC仍是公开的难题,甚至对于平面图,TCC也没有被彻底解决. 1992年,张忠辅等[11]在总结前人成果的基础上提出了一些问题并归纳了当时研究全着色的一些方法,包括穷举法,转换成边着色的方法,转换成全图的方法,匹配理论和其它的一些构造方法.经过多年的研究,尽管又产生了一些新的方法,但是也都是些基于组合的方法,而且大部分只适用于特殊的图类,所以扩展性不强.对于平面图来说,利用放电策略寻找可约的不可避免集的方法,已经证明了TCC对几乎所有的平面图成立,只有最大度为6且含4-圈的特殊情况没有解决.作者相信利用放电法能够最终解决这种情况,但是设计放电规则是一个难点,需要提出创新的思想和方法才行. 作者在研究全着色的过程中,考虑过通过设计全着色的色多项式来研究TCC.我们的出发点是希望能得到和点着色的色多项式一样的公式,然后利用代数的知识来研究全着色.目前的研究还没有成型,因此也希望感兴趣的读者在这方面贡献力量.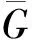
2⎣n/2」+1≤T(G)
n≤T(G)3 第一类图和第二类图
3.1 完全图和完全多部图
3.2 密集图

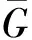



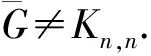
3.3 积图
3.4 弦图

3.5 立方图
3.6 其它图类
4 平面图的全色数
5 计算复杂性

6 结束语
