辛安泉泉水流量的预测分析
——基于spss软件与多元线性回归理论
2019-12-23
(长治市水文水资源勘测分局 山西长治 046000)
1 研究区概况
辛安泉域位于山西省东南部,太行山中段西,总面积10 950 km2,长治市除沁源县、武乡县一部分外,其余行政区均属于辛安泉域,是山西省第二岩溶大泉。辛安泉泉域属暖温带大陆性季风气候,多年平均气温9.4℃。多年平均降水量541.6 mm(多年指1980-2017年,下同),多年实测泉水流量2.04 m3/s,平均开采量2.04 m3/s,经还原后多年平均天然资源量8.04 m3/s。
辛安泉是一个完整的水文地质单元,具有独立的补、径、排系统,大气降水是该系统主要补给来源,通过降水入渗,地表地下汇流,在潞城区、黎城县、平顺县三县区交界的浊漳河干流河谷附近以泉水形式排泄[1]。
根据辛安泉域补径排条件,将该岩溶水系统划分为黎城子系统、襄垣子系统、长治子系统、壶关子系统、平顺子系统、径流滞缓区六个子系统。黎城子系统位于排泄区北部,子系统面积630 km2;襄垣子系统位于排泄区北部,东部以上遥背斜下寒武统为隔水边界,西部与径流滞缓区相连,北部以地下水分水岭与娘子关泉域为界,子系统面积1 440 km2;长治子系统位于长治新裂陷盆地的东部,其东边隔晋获褶断带与壶关子系统为邻,西边与径流滞缓区相连,南边以地下水分水岭与延河泉域分界,子系统总面积为980 km2;壶关子系统位于排泄区南部,西部隔晋获褶断带与长治子系统为邻,南部与三姑泉域分界,东部以地表分水岭与平顺子系统相连,子系统面积1030km2,平顺子系统位于排泄区东南部,其东边和南边都是泉域的隔水边界,西部以地形分水与壶关子系统相连,子系统面积620 km2;该区位于岩溶水系统西部的沁水古生代沉降带内,其西部、北部为地表分水岭,东部北段和南段分别与襄垣子系统和长治子系统相连,北部和南部分别与娘子关泉域和延河泉域为邻,全区面积6 250 km2,占泉域总面积的57%。区内寒武、奥陶系碳酸盐岩含水层埋藏数较大,可溶岩裂隙不发育,地下水径流滞缓或处于滞流状态[2]。辛安泉域岩溶地下水子系统特征图如图1。
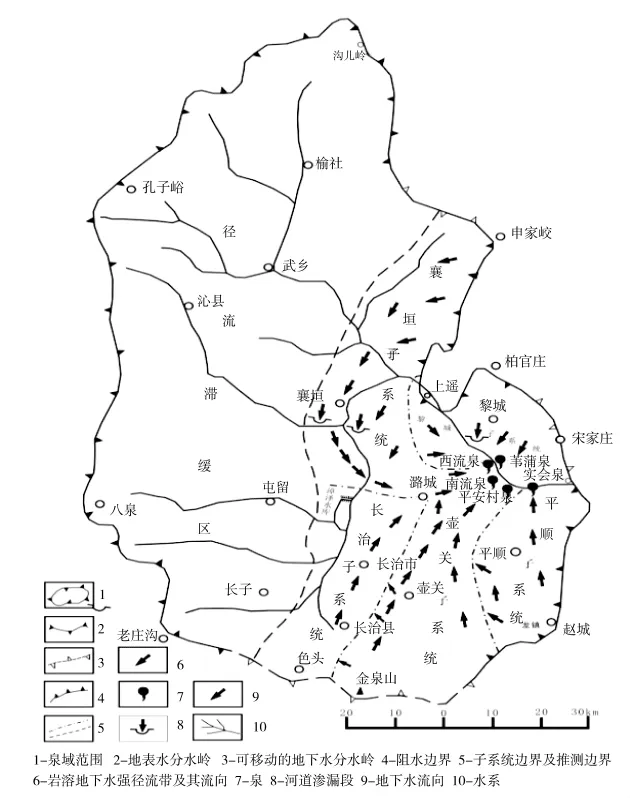
图1 辛安泉域岩溶地下水子系统特征图
2 泉水实测流量变化影响因素
实测泉水流量受降雨量、开采量影响,并且泉域不同子系统地下水位的变化往往能反应泉水天然资源量的多少。
2.1 降水量
根据泉域水文地质条件,裸露岩溶区的降水垂直入渗是辛安泉泉水主要补给来源,因此,当年降水量的多少能够影响泉水流量。除此以外,流经碳酸盐岩裸露区和半裸露区的河流渗漏也是岩溶地下水的补给来源之一,经过大气降水,入渗,以及在复杂的地下水动力条件的地下水流动,降水量对泉水流量的影响往往具有时滞性。因此对比分析当年降雨量,以及考虑前期降水影响(前一年、两年)降水量与年泉径流深的趋势变化,趋势变化图如图2。考虑不同时期的前期降雨影响的降雨量结果如表1,并由结果可知考虑前一年前期降水影响的降水量,与年泉径流深具有更好的对应关系。
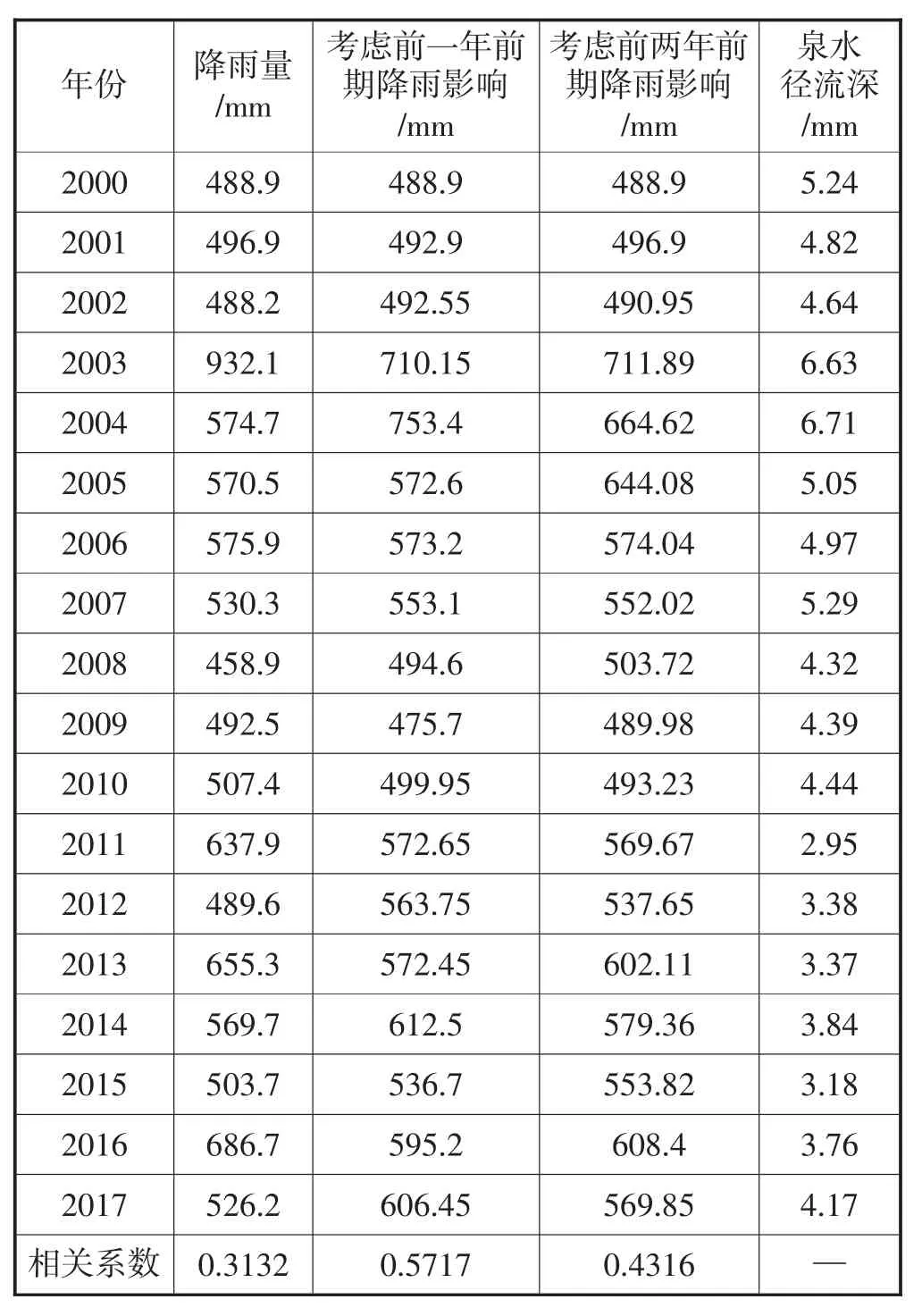
表1 辛安泉考虑前期降雨影响降雨量与泉水径流深表相关系数及数据表
2.2 不同子系统地下水水位分析
除平顺子系统、壶关子系统外,其余四个子系统分别选择一个代表地下水水井,排泄区选择D3、E5两个地下水水井,并收集2000-2017年17年水位年值资料。绘制六个水井逐年年均水位对比图(图3),其年变幅一致,具有代表性。
3 多元线性回归模型构建

图2 辛安泉考虑前期降雨影响降雨量与泉水径流深趋势变化图

图3 各系统代表观测水井逐年水位对比图
影响某因变量Y的自变量往往不止一个,选择一些对因变量有显著影响的变量X1、X2、X3…Xn作为自变量,应用多元线性回归方法,建立“最优”的回归方程[3]:式

中:b0、b1、bk为待估的回归系数;i=1、2、…n(n是样本容量);ui为随机误差。
SPSS统计分析软件的基本功能包括数据管理、统计分析、图表分析、输出管理等等。统计分析过程包括描述性统计、均值比较、一般线性模型、相关分析、回归分析、对数线性模型、聚类分析、数据简化、生存分析、时间序列分析、多重响应等几大类。
借助数据分析SPSS软件,采用其中的分析-回归-线性。构建多个自变量(①滞缓区水位X1、②长治子系统水位X2、③襄垣子系统水位X3、④黎城子系统水位X4、⑤排泄区D3水位X5、⑥排泄区E5水位X6、⑥考虑前一年降雨影响降雨量X7、⑦开采量X8)与单个因变量Y(辛安泉实测流量)的线性关系。
相关参数分析结果如下,表2列出了自变量在回归方程中的偏回归系数b0、标准误差、标准化偏回归系数b、回归系数检验的t统计量观测值及相应的概率sig。b0表示各个自变量在回归方程中的系数,该数值越大,表明对自变量的影响越大,常数项值为-44.248。表3模型汇总表中R表示拟合优度,它是用来衡量估计的模型对观测值的拟合程度,它的值越接近1说明模型越好,结果最终调整R2为0.763,表示对应自变量一共可以解释因变量76.3%的变化。
通过模拟,根据回归方程系数结果建立多元线性回归方程为:
Y=-44.248+0.472X1-0.409X2-0.02X3+0.047X4+0.363X5+0.382X6+0.007X7-1.51X8
4 结果分析
由表2中回归方程系数可以看出,排泄区以及开采量对实测泉流量影响较大,而降雨量由于其滞后效应,影响较小,符合实际情况。经T检验,黎城子系统水位X4、考虑前一年降雨影响降雨量X7、开采量X8的概率P值分别为0.080、0.019和0.037,按照显著水平0.1的情形下,只有此三个变量具有显著性意义,而造成其他变量显著性不强的原因可能是样本容量太小。由表3模型拟合度检验表可以看出,R和R2均接均近于1,表明模型拟合度较好。

表2 多元线性回归分析参数设置

表3 模型拟合度检验表

表4 辛安泉流量Y多元线性回归分析模拟结果
用已建立的多元线性回归方程,预测2000-2017年实测泉流量值,预测结果如表4。与实测值进行对比,相对误差除2011年为28.8%,其余均小于20%,平均相对误差0.9%,预测效果比较满意。
5 结语
建立辛安泉实测泉流量模型,由于所收集的资料系列短,缺少壶关子系统、平顺子系统水井水位资料,并且传统地下水井为人工观测、统计,可能对辛安泉流量预测产生影响。
SPSS多元线性回归分析时如果有两个或者两个以上存在线性相关关系,会产生多重共线性关系;采用进入法,未进行逐步进入,相关关系不强的因子未进行剔除。因此,该模型预测值仍需与常规水量还原法进行对比,具体应用适用于缺测、漏测情况下插补值的计算。
