基于幅相分离和动态粒子群算法的SAR图像属性散射中心参数估计

张 华, 张素莉, 何树吉

(1.长春工程学院, 吉林 长春 130012;2.重庆电子工程职业学院，重庆 401331)

0 引 言

高频区雷达目标的电磁散射特性呈现为局部现象，即散射中心模型。目标整体的散射场等价于若干散射中心的散射效应之和[1-2]。精确提取SAR图像中目标的散射中心并分析其参数对于了解目标特性，进行目标识别等应用具有重要意义。针对散射中心的参数化建模问题，研究人员先后提出了指数衰减模型[3]、几何绕射模型(GTD模型)[4]以及属性散射中心模型等经典模型[5]。文献[6]对基础散射源的参数化模型进行了全面的归纳和分析。属性散射中心由于其参数具有明确的物理意义自提出以来得到广泛关注，并在SAR目标识别中得以成功运用[7-9]。属性散射中心的参数估计问题就是从回波数据中提取出散射中心并对其参数进行估计。但是，由于属性散射中心模型中参数数量的增加，其参数估计也存在更大的难度。针对属性散射中心模型参数估计问题，研究人员展开了广泛研究。Moses等在提出属性散射中心模型之处就设计了图像域的最大似然参数估计(MLE)方法，通过图像域的解耦和序惯估计获得目标的属性散射中心集[5,10]。计科峰等针对传统MLE方法进行了改进，进一步提高了估计精度[11-12]。文献[13]在属性散射中心的参数估计中考察了方位特性的影响。文献[14]设计了独立属性散射中心降耦合的参数估计方法。文献[15]将稀疏表示算法引入属性散射中心参数估计，提高了参数估计的效率。

常用的基于图像域的最大似然估计(MLE)算法主要分为5步[1]：图像分割、模型定阶、结构选择、参数初始值选择和参数优化。本文主要针对其中的参数优化做了改进。在完成图像分割后，可以得到单个散射中心的图像域数据进而可以得到其对应的频域数据(忽略加窗带来的影响)。从属性散射中心的表达式可以看出，位置参数仅仅与频域数据的相位有关而与幅度信息无关，因此本文采用了幅度和相位分离优化的方法，利用相位信息实现位置参数的估计，利用幅度信息实现其它参数的估计。同时针对幅度、相位分离后得到的较为简洁的参数表达式，采用了粒子数量可变的动态粒子群算法大大提高了参数优化的效率。理论分析表明，该方法可以进一步避免优化陷入局部极值。仿真实验证明了该算法的有效性。

1 属性散射中心模型

属性散射中心模型是基于几何绕射理论和物理光学理论提出复杂目标电磁散射特性描述模型[5]，其基本形式如公式(1)所示。

(1)

其中，E(f,φ;θ)为目标的总散射场；Ei(f,φ;θi)表示单个散射中心的散射场；p为模型阶数，即散射中心的数目。对于单个属性散射中心，其参数化模型表述如下：

(2)

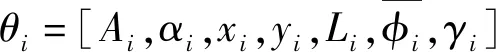
属性散射中心模型与GTD模型相比能够更精确的描述目标的电磁散射特性，但是其函数形式要更为复杂，不能够转化为谐波信号形式的通用模型。并且，属性散射中心模型含有多种不同类型的参数，给参数估计带来了很大的挑战。Mose等在提出属性散射中心之处就设计了图像域的极大似然[1]估计(MLE)方法并在实测MSTAR SAR图像上得到了有效验证。对于观测数据D(f,φ)，可采用公式(3)对其进行描述：

D(f,φ)=E(f,φ;θ)+N(f,φ)

(3)

则极大似然参数估计为：

(4)

所以，问题转化为运用数值方法求解参数集θ使代价函数J(θ)最小化的过程，即近似极大似然方法。

2 属性散射中心极大似然估计方法

MLE参数估计方法的过程如图1所示，主要涉及五大问题：(1)图像分割，即分离出独立的散射中心的响应区域；(2)模型定阶，要分割出多少个散射中心算法结束；(3)结构选择，属性散射中心模型分为局部式和分布式散射中心，对于分割出的散射中心需要确定其类型；(4)参数初值求解，用数值优化算法求解模型参数，需要提供参数的初值；(5)参数优化，根据参数初值对目标代价函数进行数值迭代，以得到更精确的参数值。由于本文主要针对参数优化进行改进，故在此只对参数优化的方法进行简要介绍。

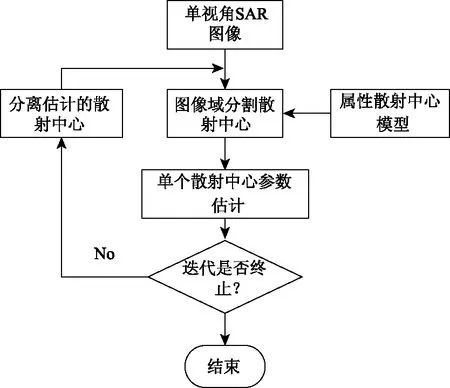
图1 参数估计流程图

在适当的初值基础上，最大似然估计算法对公式(5)中的代价函数进行最小化优化。由于噪声的协方差矩阵难以预测，通常采用公式(6)中的代价函数进行后续优化。

(5)

(6)

3 基于幅度相位信息解耦和动态粒子群算法(DPSO)的参数优化方法

3.1 幅度相位信息解耦以及参数的分离估计

对属性散射中心模型表达式做一个简单的变换，分离其幅度与相位得到：

exp(-2πfγisinφ)

(7)

3.2 动态粒子群算法(DPSO)

3.2.1基本粒子群算法

James Kenney和Russell Eberthart于1995年提出粒子群算法PSO(Particle Swarm Optimization)并在优化领域得到广泛运用。作为一种随机全局优化方法，该算法具有实现简单、搜索维数高、调节参数少、以及普适性等优点。基本粒子群又换算法的过程如下。

首先在D维的优化空间随机生成一个N个粒子的群体。经过t次迭代，其中第i个粒子的位置和速度向量分别如下：

(8)

每一次迭代中，粒子通过跟踪两个极值实现自身更新：一个是粒子自身获得的最优解，即个体极值Pi=(pi1,pi2,…,piD)；另一个是整个粒子群获得的最优解，即全局极值Pg=(pg1,pg2,…,pgD)。更新过程如公式(9)所示：

vid=ωivid+c1(pid-xid)+c2r2(pgd-xid)

xid=xid+vid

(9)

其中i=1,2,…,N,d=1,2,…,D。c1和c2为学习因子；r1和r2是在[0,1]范围内服从均匀分布的随机数；ωi为惯性因子。

3.2.2动态粒子群优化算法

上述的基本粒子群算法中，部分粒子在迭代过程中个体极值的适应度与全局极值对应的适应度相差甚小。由此，在经过若干次迭代后，便可以收敛到全局极值。反之，对于个体极值适应度与全局极值适应度相差较大的粒子，迭代次数则会显著增加并且这些粒子的迭代更新难以提供有价值的信息。因此，在每一次迭代收敛过程中，将个体极值适应度相差较大的粒子抛弃，能够有效降低后续迭代中的时间复杂度。但是，粒子数量的减少会导致算法陷入局部最优解，在此情况下，通过设计粒子数量可变的动态粒子群算法中(DPSO)[21-22]中，对每一个粒子的个体极值进行变异，能够有效避免陷入局部最优解。

3.3 基于幅度相位分离—动态粒子群算法(DPSO)的参数优化

3.3.1离散参数的连续化

为了使混合参数估计任务获得计算上的简化，首先将离散参数αi∈[-1,-0.5,0,0.5,1]连续化。连续化的参数估计可以采用一般的优化方法。对于估计得到的连续参数，本文采用最近邻原则将其映射为最可能的离散数值。

3.3.2基于DPSO的参数优化

对单个散射中心的频域数据分别提取幅度与相位信息，利用DPSO分别对幅度和相位分别进行优化得到参数优化的结果。

基于4.2.2中DPSO的描述，实现DPSO的算法如下：

定义1 迭代过程中，保留下的粒子称为活动粒子。

定义2 设Yb(n)为活动粒子个体极值的适应度，其中N为当前活动粒子数量。定义截断阀值T：

T=min(Yb(n)+(max(Yb(n)-min(Yb(n)))*R

(10)

其中R为截断比率，且R∈[0,1]。

将当前活动粒子中个体极值低于T的部分作为下次迭代中的活动粒子，同时抛弃其它粒子。

具体实施过程如下：

Step 0：参数初始化

初始化粒子群的数量M，最大迭代次数N，最大权重ωmax，最小权重ωmin。

Step1：粒子群初始化

i=1,2,…,M为粒子编号，d={1,2,…,D}为粒子维数，最大维数为D。rand函数根据参数的初值在初值的一定动态方位内实现粒子位置初始化。

Step2：粒子更新(第t+1此迭代)

Step3： 对粒子的个体极值变异：pid=pid*(1+rand)

Step4： 对粒子进行筛选(第t+1次迭代)

·计算筛选阀值：T=min(y(pid))+(max(y(pid))-min(y(pid)))·R

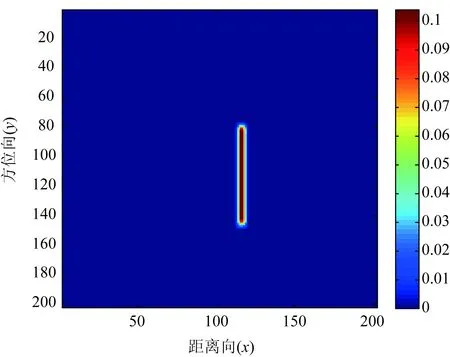
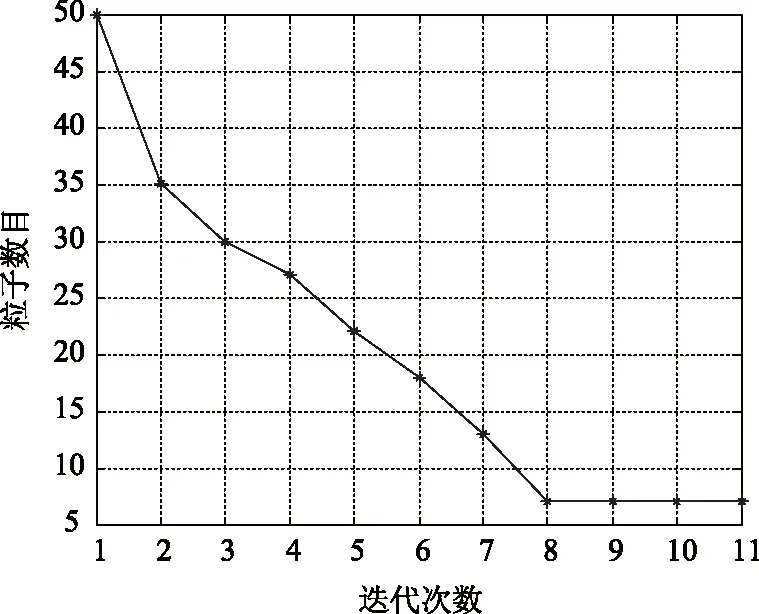
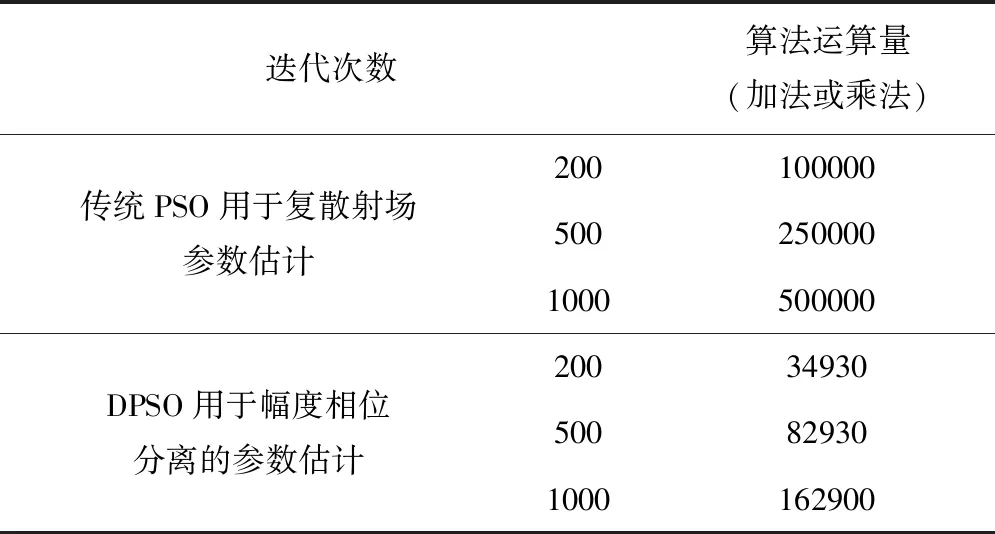
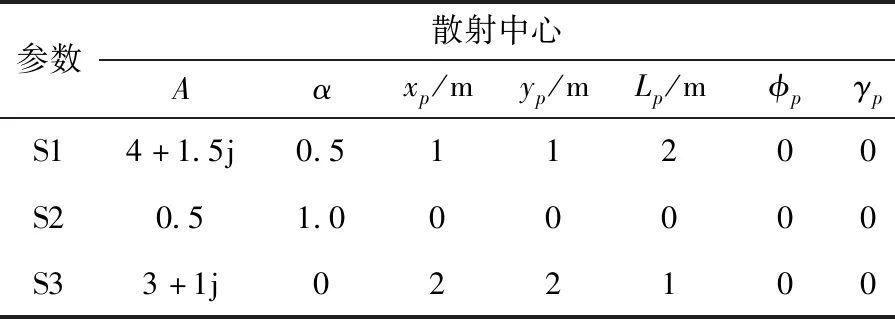
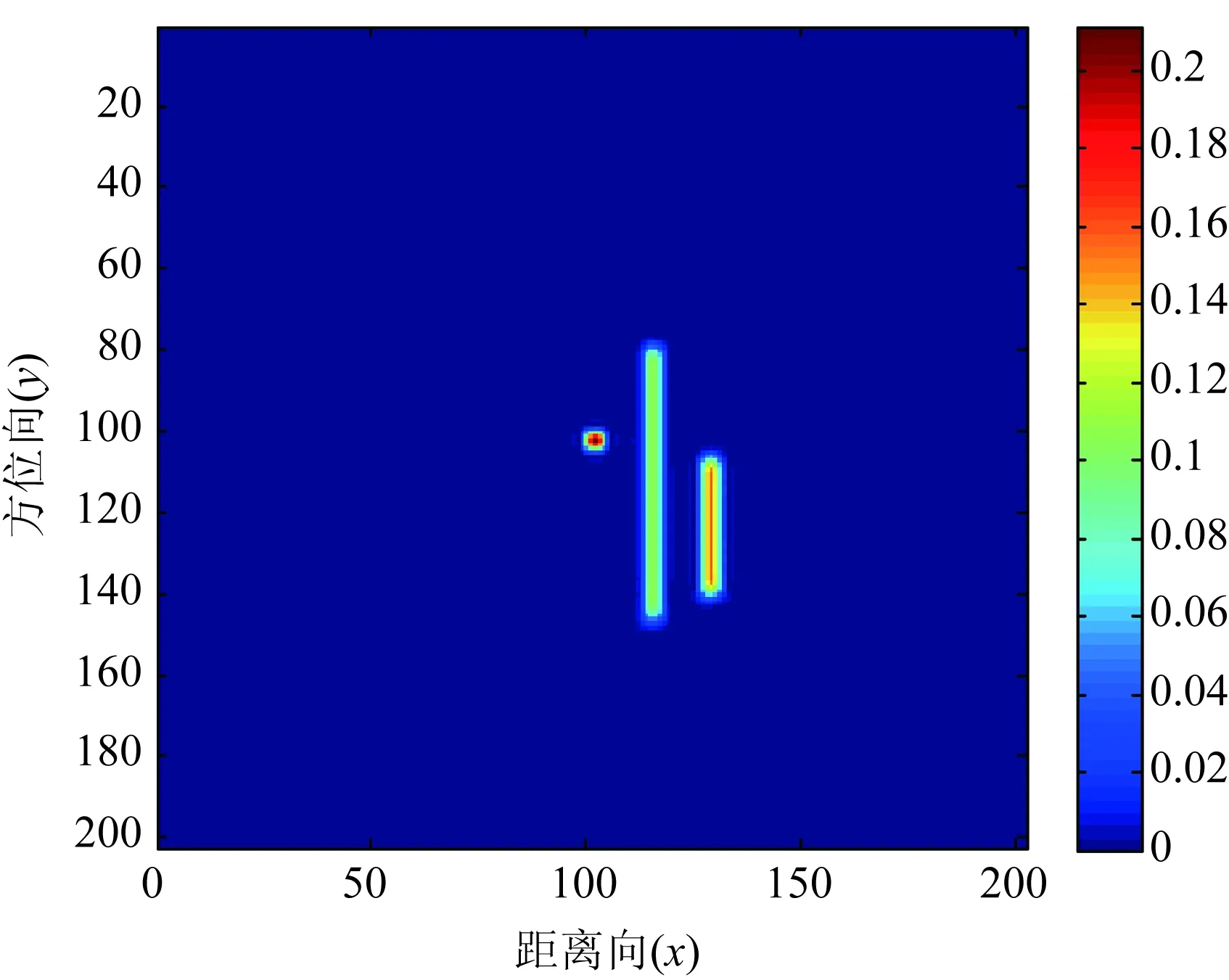
·筛选活动粒子，下一次迭代中，活动粒子的编号几何为：I={i|y(pid)

Step6：检查迭代次数是否超过最大迭代次数，如果没有达到则返回Step2，否则停止循环。

(1)利用相位信息实现对位置参数xi，yi，频率依赖因子αi和复幅度相位ω的优化

pi/2·αi+ω

(11)

利用参数初始化过程中的参数初始值限定粒子位置的初始化，利用DPSO算法优化位置参数xi，yi，频率依赖因子αi和复幅度相位ω。

(12)

3.4 算法性能分析

通过将频域数据幅度、相位信息分离，实现了参数估计式的简化，避免了复杂的复数运算，同时可以避免位置参数和其它参数之间的互扰，一定程度上降低了优化算法陷入局部极值的风险。采用了粒子数量可变的动态粒子群算法，降低了算法的时间复杂度。无论是传统的PSO还是DPSO，在优化多峰值函数是都可能出现陷入局部极值的情形，对于峰值越多的情形，其陷入局部极值的几率越大。本文采用幅度与相位分离进行参数估计，可以有效简化优化函数的表达式从而一定程度上避免陷入局部极值的情形以及加快算法的收敛速度。

本文采用算法平均计算复杂度对传统PSO算法和本文采用的DPSO算法在属性散射中参数估计中的时间性能进行理论分析和比较。对于两种PSO算法，假设第i步的粒子数量为Ni(i=1,2…m)，m为最大迭代次数。假设每个粒子每次迭代需要的运算时间为TT。

(1)传统PSO用于复散射场的参数估计分析

对于传统的PSO算法，其每次迭代的粒子数量不变。因此有N1=N2=N3=…=Nm=N。则可以得出传统PSO算法所需要的运算时间为m×N×TT。根据4.2.1中对传统PSO的介绍可知，一次粒子更新所需要的运算如下：5次加法运算，5此乘法运算和一次复散射场参数表达式的代入运算。假设一次加法和一次乘法的时间分别为Ta和Tm，复散射场参数表达式的代入运算时间为Tc，则传统PSO完成参数估计所需要的时间为：

N×m×(5Ta+5Tm+Tc)

(13)

(2)DPSO用于幅度相位分离的参数估计分析

对于DPSO算法，随着迭代次数的增加，粒子数量逐渐减小。即N1≥N2≥N3≥…≥Nm。

根据4.3.2中对于DPSO的介绍，一个粒子进行更新、变异所需要的运算如下：7次乘法运算，8次加法运算、一次散射场幅度参数表达式的代入运算和一次散射场相位参数表达式的代入运算。记一次加法和一次乘法的时间分别为Ta和Tm，一次幅度表达式代入运算和一次相位表达式代入运算的时间为TM和TP。则DPSO完成参数估计所需要的时间为

(8Ta+7Tm+TP)

(14)

在幅度相位分离后，可认为幅度表达式和相位表达式的代入运算的时间相近，即TM≈TP，对比整个复散射场的参数表达式可认为TM≈TP≈Tc/2。则DPSO所需要的时间为

(15)

由于幅度表达式和相位表达式的形式简单，在达到同样参数估计精度的情况下，其所需要的迭代次数更少，并且随着迭代次数的增加，粒子数量不断减小。因此，DPSO用于幅度相位分离的参数估计可以减少参数估计的运算量。实验统计也证明了这一点。

4 实验与分析

本节中采用单个独立散射中心和多个散射中心的仿真数据进行验证实验。中心频率fc=9.0e9，带宽1.0e9，成像孔径5度，成像点数Mz=Nz=202。单个独立散射中心用于定量计算本文算法的时间效率，多个散射中心用于评价本算法进行属性散射中心模型参数估计的有效性和可靠性。

4.1 单个独立散射中心实验

单个独立散射中心的参数设定如下：

表1 单个独立散射中心参数设定

单个散射中心的成像结果如图2。

图2 单个散射中心成像结果

对DPSO和基本PSO算法的参数设置如下：最大迭代次数1000；初始粒子数量N=50；学习因子c1=c2=2，最大和最小惯性系数分别为ωmax=0.9,ωmin=0.4。其中对DPSO的截断比率设定为R=0.5。利用DPSO对幅度相位分离估计时的平均粒子数量变化记录如下：

幅度表达式平均粒子数量变化如图3。

图3 幅度表达式优化的粒子数目变化曲线

相位表达式平均粒子数量变化如图4。

图4 相位表达式优化的粒子变化曲线

由此可见，幅度和相位的优化表达式在经历若干次迭代后粒子数剧烈减少到某一稳定值，在迭代次数较多的情况下，DPSO可以大大减少运算量。

传统PSO和DPSO用于参数估计的时间效率记录如表2。

表2 算法运算量统计

两种方法用于参数估计的结果记录如下(参数A仅记录幅度)：

可见，在迭代次数较小的情况下，传统PSO和DPSO的优化性能都较差且DPSO的性能要差于PSO，这是由于粒子数目的减少导致的性能下降。在相位信息分离后，位置参数的估计在迭代次数较小时即可以取得较好的估计性能。随着迭代次数的增加，DPSO和PSO的性能逐渐提高并且逐渐接近，均能达到较佳的优化性能。

表3 参数估计结果

4.2 多个散射中心实验

多个散射中心的参数设置如表4。

表4 多个独立散射中心参数设定

多个散射中心成像结果如图5。

两种方法用于参数估计的结果记录如下(复幅度仅记录幅度)：

图5 多个散射中心成像结果(单位:dB)

表5 参数估计结果

多散射中心参数估计的实验结果同样证明了本文方法的有效性。与传统的PSO优化复散射场实现参数估计相比，本文采用的幅度——相位分离的DPSO方法在运算量大大减小的情况下并没有带来参数优化性能的下降，因此具有实用价值。

5 结 语

本文针对属性散射中心模型参数估计的问题，提出了一种基于幅度相位分离和动态粒子群的快速参数估计方法。利用位置参数仅仅与相位相关的特点采用了幅度与相位分离的参数估计策略一定程度避免了参数之间的互相影响。对于分离后的较为简单的参数优化表达式，采用了粒子数量可变的粒子群算法，该算法可以大大减少粒子群算法的运算量，达到快速实现参数估计的目的。实验结果表明，该方法可以取得较好的参数估计效果。