基于模糊时间序列的农用拖拉机总数量预测
2019-12-21王炎林胡陈君郑延莉曹中华方晶晶罗泽勇
王炎林,陈 建,王 卓,胡陈君,郑延莉,曹中华,方晶晶,罗泽勇
(西南大学 工程技术学院,重庆 400716)
0 引言
农用拖拉机总数量指现有的投入农业生产的拖拉机总台数,是衡量我国农业机械化水平的一个重要指标[1-2],也是我国农机行业制定生产与销售规划的参考。2017年上半年,由于农机补贴购置影响,农产品价格下滑和农民购买力和购机意愿下降,拖拉机总产值同比下降18.33%,而大中型拖拉机的库存率达到114%,供需矛盾极为突出。因此,合理地预测我国农用拖拉机总数量发展趋势并为拖拉机的发展提供建议便显得尤为重要。
农用拖拉机逐年总数量由于受到政府政策(如购机补贴、排放标准,土地整治等)的影响,无法用一个准确的数学公式预测其发展趋势,其实质上是一个模糊时间序列的集合。采用平均法、指数平滑法、季节分析法[3]存在着明显的不足,而已有的模糊时间序列模型难以同时兼顾精度和计算的简便性。为此,通过改进一种模糊时间序列模型,简化计算,降低平均预测误差率,得到较为准确的农用拖拉机总数量预测模型,并与其他经典模型进行对比,旨在对我国农用拖拉机发展提供建议。
1 模糊时间序列计算方法
1.1 模糊时间序列
时间序列是指某种现象的某一个(或多个)统计指标按时间先后顺序排列而形成的数据序列(如股价、国民收入、商品销售等),但传统的经典时间序列无法处理模糊不清、不精确的现实问题[4]。1965年,美国自动控制专家Zadeh教授提出了模糊理论和模糊逻辑概念,并初步建立了处理带有不确定的、模糊的语言的数学模型[5]。1994年,Song和Chissom运用Zadeh[6-8]提出的模糊集理论,建立了针对模糊时间序列的预测模型,预测每年入学学生数量,开创了模糊时间序列及其应用的先河。
模糊时间序列的核心便是模糊区间的划分和对模糊关系的处理。2006年,Li-Wei Lee提出一种改进型时间序列,预测多因素影响的时间序列,计算精度较高,平均误差率仅为0.26%。2007年,Tahseen Ahmed Jilan提出了一种改进的模糊时间序列,预测道路交通事故,其平均误差率达到2%[9-10]。之后,Shiyi、Duru等学者改进隶属度函数或加权处理差分论域值,提高了计算精度[11-12]。
经典的Song模糊时间序列定义如下:对任意一个固定的Y(t)(t=0,1, 2,...),设Y(t)为实数域的子集,Y(t)上定义了一组模糊集fi(t)(i=1,2,...),且F(t)={f1(t),f2(t),...},则称F(t)为定义在Y(t)上的的模糊时间序列。
1.2 论域与检验公式
定义A为论域,将论域A划分为有限个有序子集,即为模糊区间,可表示为A={A1,A2,…,Ai}(i=1,2,…,n)。将论域A逐年差分,得到论域A的差分论域ΔA={ΔA1,ΔA2,...,ΔAi},差分计算方法为
ΔAi=Ai-Ai-1
(1)
计算论域A的差分论域的单位分割,并根据论域A的差分论域中的最大值,向下取整,分割论域[13]。分割方法为
V1=max(|ΔAi|)/m
(2)
Ui=i·V1(-m≤i≤m)
(3)
其中,m选取过大会造成差分论域的分割论域过大,增加计算量;m选取过小,难以将数据分离。针对选取的数据,通过计算比较选取。
论域A差分的分割论域为
U={Um,,...,U0,...,U-m}
在完成A的论域、差分论域、分割论域的建立后,建立模糊数和逆模糊公式[14-15]。
其中,模糊数表示为Ti,公式为
(4)
其中,Ui的选择根据差分论域匹配。
对应的逆模糊数表示为Si,公式为
(5)
论域A中元素的预测计算公式为
Gi=Ai-1+Si
(6)
应用上述预测模型,不仅可以验证论域A中元素历史数据,还可以预测其未来数据,但两者的侧重点及对模型的要求不一样。前者需要考虑预测模型的预测误差率,后者则是侧重对预测模型中元素增长率的预测。
预测历史数据的绝对预测误差率表示为
(7)
由于论域A中的逐项的绝对预测误差率均不相同,选择最大绝对预测误差率来刻画预测模型的精度是不合理的,选择平均预测误差率AFER(Average Forecasting Error Rate)加权表示预测模型精度。AFER计算公式为
(8)
逐项增长率表示为
(9)
当εi>0时,表示第i项相对于第i-1项,论域A中元素相对于上一项元素呈增加趋势,增长εiGi-1;当εi≤0时,表示第i项相对于第i-1项,论域A中元素相对于上一项元素成减小趋势,减少-εiGi-1。
2 全国农用拖拉机总数量预测
2.1 数据来源与论域
根据中华人民共和国国家统计局公布的数据,选择全国1997-2016年农用大中型拖拉机总台数、农用小型拖拉机总台数为样本数据[16],并得到农用拖拉机总台数,如表1所示。

表1 1997-2016全国农用拖拉机总台数Table 1 Total number of agricultural tractors nationwide 1997-2016
根据公式(1),计算得到农用拖拉机总数量逐年差分论域,即
Δ={771902,840959,831518,262497,424814,452062,910299,996982,732345,856636,1965437,805473,754856,739490,305566,-31700,184200,126100,66395}
计算表明:当选取m=100时,能较好地区分开差分分割论域集合。
根据公式(2),计算得出V1=1965437/100=19654.37。如果以万台作为单位,则V1=1.965 437,得到全国农用拖拉机总数量的逐年差分的分割论域U。U为首项为-196.543 7、末项为196.543 7、公差为1.965 437的等差数列,则
U={-196.5437,-194.578263,…,0,…,196.5437}
2.2 验证历史数据
在验证历史数据的时候,最关键的便是找到匹配的Ui。在计算某年全国农用拖拉机总台数时,应用不同的Vi,能得到201个不同的预测值,从这个201个预测值中找出最接近该年的真实值的数据作为预报值。假如预测1999年农用拖拉机总台数,首先计算模糊数和逆模糊数,即
逆模糊数为
预测1999年农用拖拉机总数量,即
G1999=A1998+S1999=1277.6317056
预测的绝对误差率δ1999=0.0814%,该组数据预测精度较高。
同理,依据上述公式求出1997-2016年全国农用拖拉机总台数历史数据,如表2所示。
计算出平均绝对误差率为0.037 2%,已经非常小。

表2 应用模型预测1997-2016年全国拖拉机总数量Table 2 Application of the model to predict the total number of tractors in China from 1997 to 2016
2.3 预测未来数据
根据公式(4)可知:预测某年农用拖拉机总数量时,需要两项数据,上年差分论域值ΔAi-1和分割论域值Ui。当预测2017年农用拖拉机总数量时,可知ΔA2016=6.6395,其关键问题确定分割论域U2016。当年份没有重大利空好消息诸(如国家政策大方向调整)时,可知U2016∈[-196.5437,196.5437],则关于2017年农业拖拉机总数量预测函数为
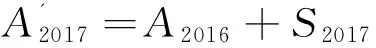
根据表2可知:2014-2016年差分论域的值分别为18.420 0,12.610 0,6.639 5,与它们接近的差分论域的分割值为U9、U6、U3;将U9、三者平均值、U3用作2017年全国农用拖拉机总数量预测的冒险预测值(RPV)、正常预测值(NPV)和保守预测值(CPV)的所用参数,可得RPV=2335.1381、NPV=2329.5234、CPV=2323.6090,并计算其年均增长率。
由表3可知:对于2017年全国农用拖拉机总数量冒险预测值为2 335.138 1万台,相对于2016年的年增长率为0.784 2%;正常预测值为2 329.523 4万台,相对于2016年的年增长率为0.539 5%;保守预测值为2 323.609 0万台,相对于2016年的年均增长率为0.286 6%。
当预测第i年(i>2017)时,要考虑误差累计效应,转化成已知最近的年份计算,即
(10)
此时,可根据差分论域中值出现的次数进行加权处理,则
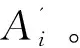
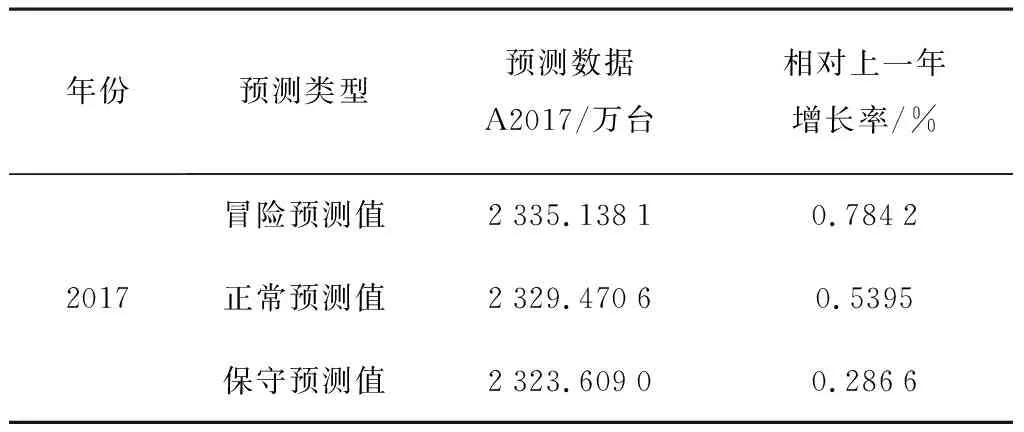
表3 预测2017年全国农用拖拉机数量及其增长率Table 3 Forecasts the number and growth rate of agricultural tractors in the whole country in 2017
2.4 模型比较
本文修正模型和Song模型和Chen模型[17]进行比较,将模糊区间划分为8份,Song模型隶属度函数为三角函数,得出模型比较结果,如表4和图1所示。

表4 本文模型与Song、Chen模型Table 4 Comparison with classical models
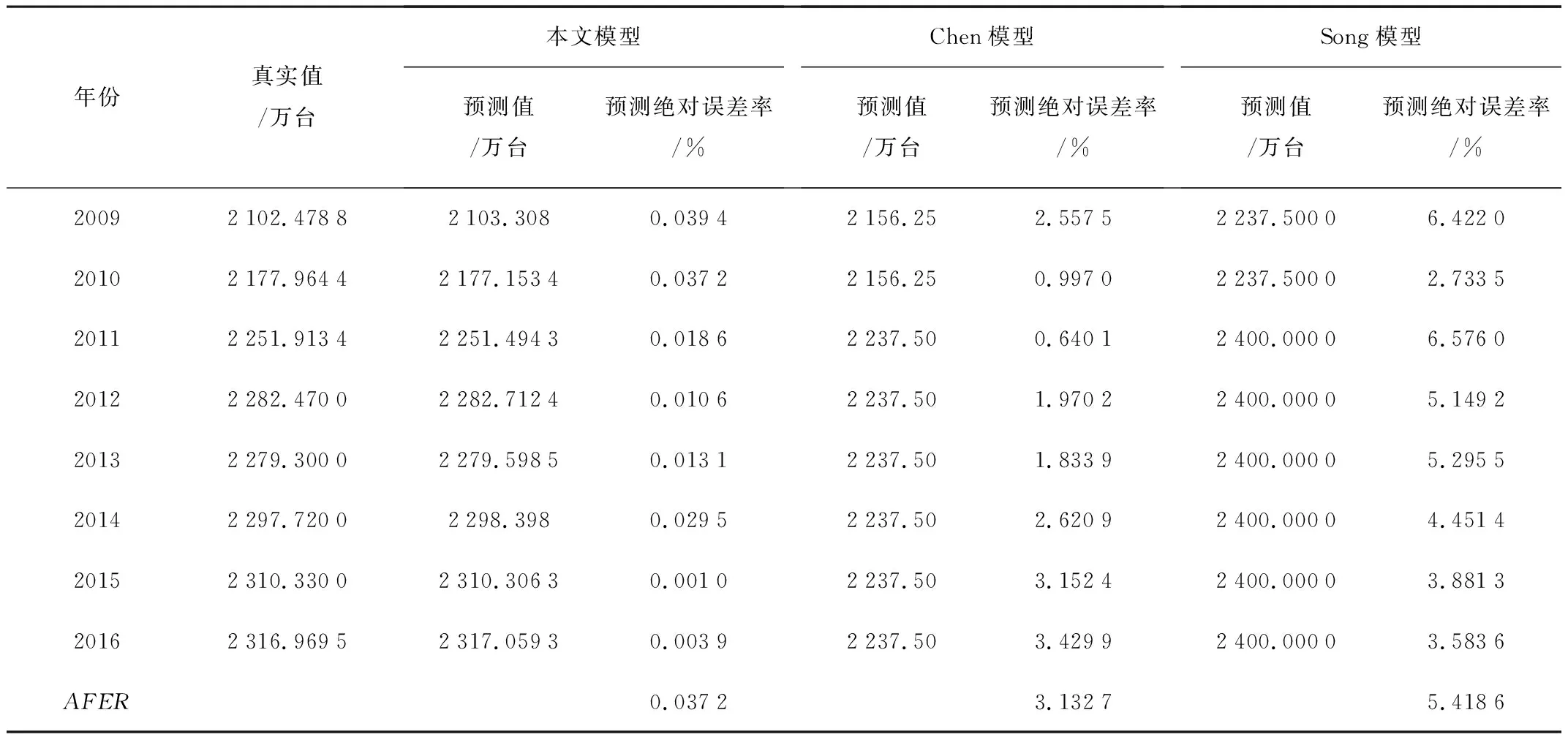
续表4

图1 模型比较Fig.1 Comparison with Song model and Chen model
由图1可知:本文模型预测的全国农用拖拉机数量的预测精确度高于Chen模型,Chen模型的预测准确性高于Song模型,且其预测趋势一致。
3 结论
基于模糊时间的预测模型是一种改进模型,且与经典Song模型和Chen模型对比,其计算过程大大简化,平均误差率提高了10多倍,使得预测结果更加接近真实值。预测结果表明,全国农用拖拉机总台数处于缓慢增长状态。同时,应用本文模型分别预测小型拖拉机和大中型拖拉机增长率及大中型农用拖拉机配套农具数,大中型农用拖拉机增长率达到6.897 3%,这与土地整治大背景下大中型农业机械取代小微型农业机械的趋势一致;大中型农用拖拉机配套农具数其正常预测值达到7.543 1%,年均增长率高于大中型拖拉机的正常预测值6.597 3%,在一定程度上反应了农用大中型拖拉机的利用率在提高。在农用拖拉机行业发展方面,国家除了宏观政策的调控与购机补贴之外,还需协调传统农机子行业与新兴子行业的发展,缓解产能过剩,加快产品结构调整,逐步解决供需失衡问题,促进我国拖拉机行业乃至我国农业机械健康发展。
